Antireflection Coating at Metamaterial Waveguide Structure by Using Superlattices (LANS) ()
1. Introduction
In many applications, reflection is undesirable and causes insertion losses, for example. It is well known that the application of one or more antireflection coating (ARC) layer on the front surface of the photovoltaic cells and optoelectronic devices (Lasers, IR diodes, etc.) reduces the amounted reflection of the incident light, which improves the device performance [1] -[3] . Antireflection coatings require a particular refractive index and quarter wavelength thickness where it operates by overcoming the mis-match between intrinsic impedances of two media. This approach is scalable over a wide spectral range from microwave to far infrared [4] . There have been a few efforts to develop antireflection coatings at THz frequencies by using dielectric meta-materials or lefthanded materials (LHM). LHM have both negative permittivity and permeability and consequently have negative index of refraction [5] [6] and are able to match media impedances. The theory of antireflection coating is examined by many authors [7] [8] . The matrix method [9] [10] is usually employed for calculation of reflection coefficient. Chen et al. [4] have presented approach of metamaterial antireflection.
It reduces the reflection and enhances transmission near a specifically frequency over a wide range of incidence angles for both TE and TM polarizations, Bouhafs et al. [3] have made a theoretical study of the antireflection coatings on silicon solar cells. Cory et al. [11] have analyzed the reflection and transmission characteristics of a multilayered structure consisting of metamaterials and dielectric slabs. In this paper, I investigate the reflection and transmission properties of a superlattices (LANS)-metamaterial (LHM)-dielectric multilayered structure. Since antireflection coating is formed by two slabs of the same thickness and of opposite refractive indices, a pair of LHM and LANS materials is situated between two semi-infinite dielectric media which are considered right handed materials (RHM) of positive refractive index. The superlattice is a lateral anti-ferromagnetic/nonmagnetic (LANS) such as . LANS are described with an effective medium theory. Such description is valid when the wave lengths of the excitations are much longer than the superlattice period where
. LANS are described with an effective medium theory. Such description is valid when the wave lengths of the excitations are much longer than the superlattice period where , where k is the magnitude of the wave vector and L = L1 + L2, is the period of the superlattice, L1 and L2 are the thickness of the anti-ferromagnetic layers and non-magnetic layers ,respectively [5] [12] .
, where k is the magnitude of the wave vector and L = L1 + L2, is the period of the superlattice, L1 and L2 are the thickness of the anti-ferromagnetic layers and non-magnetic layers ,respectively [5] [12] .  and
and . In the theory the electric and magnetic fields of the incident waves are determined in each region by Maxwell’s equations. Then Snell’s law is applied and the boundary conditions are imposed at each interface to obtain the reflection and transmission coefficients. The reflected and transmitted powers of the structure are presented in terms of these coefficients. In the numerical analysis, a recursive method [13] is used to calculate the reflected, transmitted powers as a function of incident wavelength, angle of incidence, layer thickness and magnetic fraction of (LANS). The calculations are performed for electromagnetic radiations in both the visible and microwave bands for a single wavelength by selecting the optimum refractive indices of LHM and RHM in both bands. The suitable LHM in each band is selected. The conservation law of energy is checked and satisfied.
. In the theory the electric and magnetic fields of the incident waves are determined in each region by Maxwell’s equations. Then Snell’s law is applied and the boundary conditions are imposed at each interface to obtain the reflection and transmission coefficients. The reflected and transmitted powers of the structure are presented in terms of these coefficients. In the numerical analysis, a recursive method [13] is used to calculate the reflected, transmitted powers as a function of incident wavelength, angle of incidence, layer thickness and magnetic fraction of (LANS). The calculations are performed for electromagnetic radiations in both the visible and microwave bands for a single wavelength by selecting the optimum refractive indices of LHM and RHM in both bands. The suitable LHM in each band is selected. The conservation law of energy is checked and satisfied.
2. Theory
Consider LHM and LANS of electric permittivity and magnetic permeability  and
and  respectively embedded between two semi-infinite dielectric media of permeability and permittivity as
respectively embedded between two semi-infinite dielectric media of permeability and permittivity as  and
and . A perpendicular polarized wave is incident on the structure at Y = 0 at angle
. A perpendicular polarized wave is incident on the structure at Y = 0 at angle  relative to the normal to the boundary as depicted in Figure 1.
relative to the normal to the boundary as depicted in Figure 1.

Figure 1. Wave propagation through a structure consisting of LHM and LANS materials inserted between two semi-infinite dielectric media.
Introducing the effective medium theory, the magnetic permeability of the LANS [5] [12] which is described as a single effective medium, can be written as:
 (1)
(1)
with

where the expressions of  and
and  are [5] [12] :
are [5] [12] :

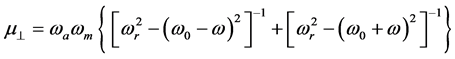
with


 represents an isotropy field,
represents an isotropy field,  the exchange field, and
the exchange field, and  the gyromagnetic ratio. m0 is the sublattice magnetization. The magnetic field of the superlattice is H0. The effective dielectric function of (LANS) is expressed by [5] [13] as:
the gyromagnetic ratio. m0 is the sublattice magnetization. The magnetic field of the superlattice is H0. The effective dielectric function of (LANS) is expressed by [5] [13] as:
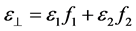
The electric and magnetic field vectors for TE waves propagating along x-axis with angular frequency ω are defined as:
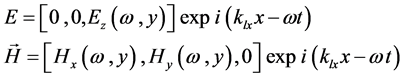 (2)
(2)
The electric field in each region is [14] , [15] :
 (3)
(3)
where  and
and  are the amplitude of forward and backward travelling waves in the region of order
are the amplitude of forward and backward travelling waves in the region of order
 ,
,  is the wave vector inside the material and
is the wave vector inside the material and  is the refractive index of it.
is the refractive index of it.
In Superlattice (LANS) Region
The curl Maxwell’s equations are [12] :

By these equations
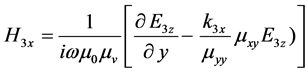 (4)
(4)
where 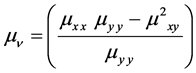 is the Voigt permeability.
is the Voigt permeability.
By Maxwell’s equation , the magnetic field in the other regions of order
, the magnetic field in the other regions of order  is:
is:

Matching the boundary conditions at each layer interface, where at ,
,  and
and 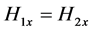 and so on yields six equations with six unknown parameters as:
and so on yields six equations with six unknown parameters as:
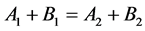 (5)
(5)
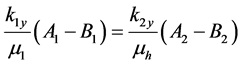 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
According to Snell’s law ,
, 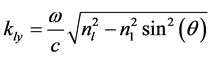
with

For TE polarized light, at the first interface, the Fresnel coefficient (interface reflection and transmission (r, t) respectively are given by [16] :
 (11)
(11)
For the other interfaces the Fresnel coefficients are:
 (12)
(12)
where ,
,
The reflection and transmission coefficients 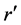 and
and 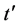 respectively of the structure are [17] :
respectively of the structure are [17] :

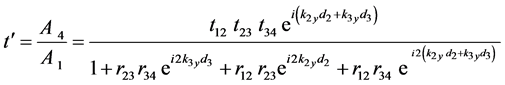 (13)
(13)
The reflectance 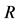 and transmittance
and transmittance  of the structure are given by:
of the structure are given by:
 (14)
(14)
where  and
and  are the conjugate of
are the conjugate of  and
and 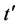 respectively.
respectively.
The law of conservation of energy is [17] :
 (15)
(15)
In this work, two cases of LHM are considered. The first when the incident electromagnetic waves in the visible spectral band and other one in microwave band. The frequency―dependent permittivity of LHM in the visible band is described by Drude medium model as [18]
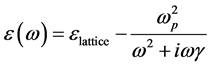 (16)
(16)
where  is the angular frequency,
is the angular frequency,  is the lattice permittivity,
is the lattice permittivity,  is the effective plasma frequency and
is the effective plasma frequency and  is the electric damping factor.
is the electric damping factor.
For microwave region, I employ a dispersive LHM with  and
and  appeared in [15] [19] as:
appeared in [15] [19] as:
 (17)
(17)
where  and
and  are the electric and magnetic plasma frequencies.
are the electric and magnetic plasma frequencies. 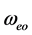 and
and  are the electric and magnetic resonance frequencies.
are the electric and magnetic resonance frequencies. 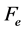 and
and  are the scaling filling parameters,
are the scaling filling parameters,  and
and  are the electric and magnetic dissipation factors.
are the electric and magnetic dissipation factors.
3. Numerical Results and Discussion
The parameters were used in carrying out the numerical calculations are [12] : the applied field H0 = 0.8 kG,  ,
,  ,
, 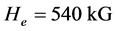 ,
,  and
and  for antiferromagnetic layers,
for antiferromagnetic layers, 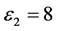 for the non-magnetic layers. The relative permeability of the dielectrics is
for the non-magnetic layers. The relative permeability of the dielectrics is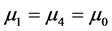 , the refractive index of the dielectrics
, the refractive index of the dielectrics  and
and .
.
3.1. In Visible Spectral Band
The parameters were used are [18] : ,
,  ,
, .
.
The relative permeability of LHM is assumed to be −1. The thickness of each slab is assumed to be one-half long of the central wavelength. The reflected, transmitted power of the structure is calculated as a function of wavelength of the incident waves, angle of incidence, layer thickness and magnetic fraction of LANS. According to (16) the real part of refractive index of LHM is negative in the wavelength range of (500, 600, 700, 1000) nm where the real part of n2 of values (−1.023, −2.34, −3.27, to −5.596) where the damping factor of LHM in this region is ignored and no energy loss is displayed. The central wavelength is assumed to be 600 nm. This choice is based on the spectral stability of the coating and for low reflectance. Stability means that the low-reflectance spectrum changes very slightly with refractive index variations as shown by Figure 2. It displays the reflected, transmitted power as a function of the normal incident wavelength when the dielectric refractive index nd changes to the values of (2.34, 4.86, 6.58). It shows maximum reflectance R of value <0.25 and minimum transmittance T of value >0.75 at nd of value 2.34 over a wide wavelength range (λ = 500 - 1000 nm). The refractive indices of LHM are (−2.34, −4.86, −6.58) at incident wavelength λ of values (600, 900, 1140) nm respectively and that of LANS is (n3 = 2.49 at λ = 600 nm and magnetic fraction ).
).  changes very slightly with frequency. For these indices, one minimum appears around λ = 600 nm at which the refractive indices of LHM, and LANS, dielectrics are approximately closed to each other and opposite in signs which confirm that high transmitted power can be achieved if
changes very slightly with frequency. For these indices, one minimum appears around λ = 600 nm at which the refractive indices of LHM, and LANS, dielectrics are approximately closed to each other and opposite in signs which confirm that high transmitted power can be achieved if ,
,  ,
, 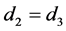 [11] . These conditions which
[11] . These conditions which
 (a)
(a) (b)
(b)
Figure 2. (a) The reflected, (b) transmitted power as a function of the normal incident wavelength when the dielectric refractive index nd changes as nd =2.34, 4.86, 6.58, f1 = 0.7, d = 250 nm.
leads to r = 0 and T = 1 around λ = 600 nm are: ,
,  ,
, 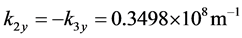 ,
,  ,
,  ,
,  ,
, . Such AR coating systems are used in photodiodes (LASER) and other optoelectronic devices which need a minimum reflectance at a single wavelength. Figure 3 illustrates the reflectance spectra over a wide range of incidence angle for λ of values (600, 700, 800) nm. In the range (θ = 0˚, 27˚) the minimum reflectance is achieved at λ = 600 nm. The implementation of LANS layer adjacent to LHM layer dramatically reduces the reflection and greatly enhances the transmission near a specifically frequency at incidence angles (θ = 0˚, 27˚). By wavelength increase to the value of 800 nm, minimum reflectance is observed at higher incidence angle of value 57˚. The effect of the magnetic fraction
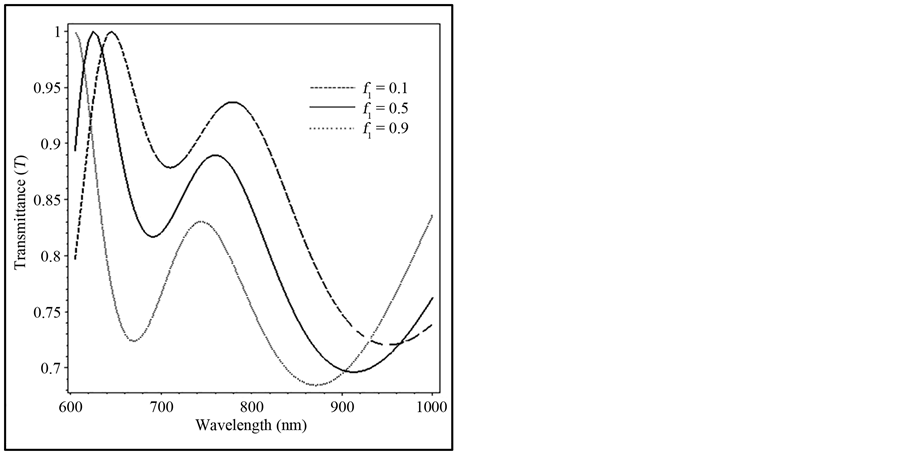
. Such AR coating systems are used in photodiodes (LASER) and other optoelectronic devices which need a minimum reflectance at a single wavelength. Figure 3 illustrates the reflectance spectra over a wide range of incidence angle for λ of values (600, 700, 800) nm. In the range (θ = 0˚, 27˚) the minimum reflectance is achieved at λ = 600 nm. The implementation of LANS layer adjacent to LHM layer dramatically reduces the reflection and greatly enhances the transmission near a specifically frequency at incidence angles (θ = 0˚, 27˚). By wavelength increase to the value of 800 nm, minimum reflectance is observed at higher incidence angle of value 57˚. The effect of the magnetic fraction  on the reflectance and transmittance is described in Figure 4. As
on the reflectance and transmittance is described in Figure 4. As  increases to the values of (0.1, 0.5, 0.9), the refractive index of LANS
increases to the values of (0.1, 0.5, 0.9), the refractive index of LANS  decreases to the values of (2.78, 2.59, 2.39) while
decreases to the values of (2.78, 2.59, 2.39) while  of LHM increases to the value of (−2.83 to −4.486) in the wavelength range (600 - 850) nm which leads to reflectance increase. It is worth to note that, R = 0 and T = 1 at λ = 600 nm, f1 = 0.9. This is because
of LHM increases to the value of (−2.83 to −4.486) in the wavelength range (600 - 850) nm which leads to reflectance increase. It is worth to note that, R = 0 and T = 1 at λ = 600 nm, f1 = 0.9. This is because ,
,  ,
, . Figure 5 demonstrates the effect of thickness d of LHM on the reflectance and transmittance at normal incidence of λ = 600 nm, 800 nm. The slab thickness is changed from 50 nm to 500 nm. It is noticed that reflectance and transmittance changes periodically with thickness. Besides that, more transmittance is realized at λ = 800 nm where maximum R is 0.03 while minimum T = 0.97 of the incident power. It is shown that the selected thickness (d = 250 nm) is appropriate for achieving zero reflectance at λ = 600 nm.
. Figure 5 demonstrates the effect of thickness d of LHM on the reflectance and transmittance at normal incidence of λ = 600 nm, 800 nm. The slab thickness is changed from 50 nm to 500 nm. It is noticed that reflectance and transmittance changes periodically with thickness. Besides that, more transmittance is realized at λ = 800 nm where maximum R is 0.03 while minimum T = 0.97 of the incident power. It is shown that the selected thickness (d = 250 nm) is appropriate for achieving zero reflectance at λ = 600 nm.
3.2. In Microwave Spectral Band
For dispersive LHM with  and
and  have parameters appeared in [15] as:
have parameters appeared in [15] as: ,
,  ,
, 
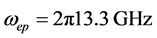 ,
,  ,
,  ,
,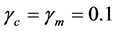 . For this LHM, the frequency range in which
. For this LHM, the frequency range in which  and
and  are negative extends from 10.4 up to 11.5 GHz with corresponding wavelength extends from 26 up to 28 mm. The thickness of each of LHM and dielectrics slabs is equal to one half-wavelength long at the operating frequency. Reflectance and transmittance are calculated numerically as stated above. The law of conservation of energy is [20] :
are negative extends from 10.4 up to 11.5 GHz with corresponding wavelength extends from 26 up to 28 mm. The thickness of each of LHM and dielectrics slabs is equal to one half-wavelength long at the operating frequency. Reflectance and transmittance are calculated numerically as stated above. The law of conservation of energy is [20] :
 (18)
(18)
where  is the loss power due to losses in LHM. Since in the structure arrangement shown in Figure 1, there is no effect of magnetic fraction of LANS on the reflected power and there is very small power loss of LHM which can’t be displayed in a figure, I rearranged the structure to be LANS in Region 1 instead of the
is the loss power due to losses in LHM. Since in the structure arrangement shown in Figure 1, there is no effect of magnetic fraction of LANS on the reflected power and there is very small power loss of LHM which can’t be displayed in a figure, I rearranged the structure to be LANS in Region 1 instead of the

Figure 3. The reflected power as a function of the angle of incidence for different wavelength λ = 600, 700, 800 nm, nd =4.86, f1 = 0.7, d = 250 nm.
 (a)
(a)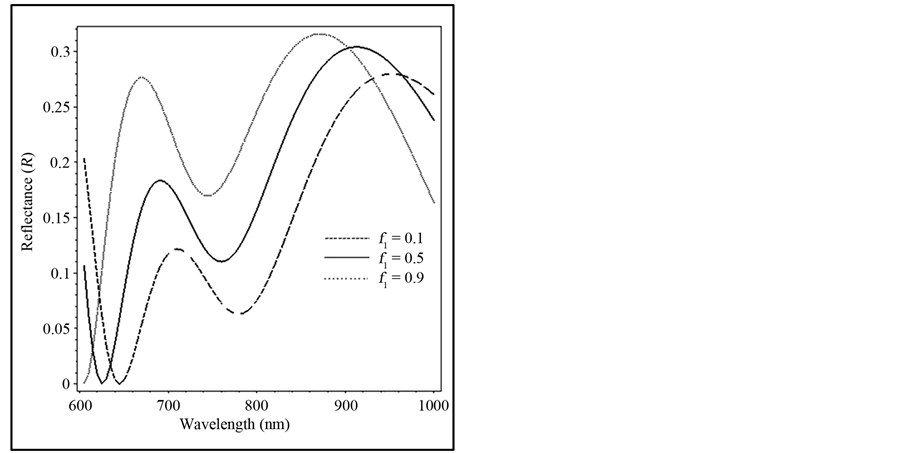 (b)
(b)
Figure 4. (a) The reflected, (b) transmitted power versus the normal incident wavelength when the magnetic fraction f1 changes as f1 = 0.1, 0.5 ,0.9, nd = 4.86, d = 250 nm.
dielectric which will be in Region 3. The reflection, transmission coefficients are rewritten as:
 ,
,

For the other interfaces the Fresnel coefficients are:
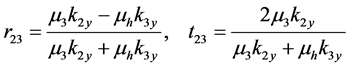

Figure 6 displays the reflectance, transmittance and power loss as a function of the incident wavelength for many values of magnetic fraction. The operating wavelength is assumed to be 0.027 m which is included in the frequency range in which  and
and  are simultaneously negative. As
are simultaneously negative. As  increases to the values of (0.1, 0.5, 0.9)
increases to the values of (0.1, 0.5, 0.9)  of LANS decreases to the values of (2.78, 2.59, 2.39) respectively,
of LANS decreases to the values of (2.78, 2.59, 2.39) respectively,  of LHM changes to the values (
of LHM changes to the values ( ) to (
) to ( ) in the wavelength range of 0.026 to 0.272 m. R = 0 and t = 1 and zero power dissipation are attained at wavelength range λ = 0.026 - 0.272 m and f1 = 0.1 at θ = 30˚.
) in the wavelength range of 0.026 to 0.272 m. R = 0 and t = 1 and zero power dissipation are attained at wavelength range λ = 0.026 - 0.272 m and f1 = 0.1 at θ = 30˚.
4. Conclusions
The transmission and reflection of perpindicular polarized waves by a multilayered structure consisting of a pair of LHM and LANS materials embedded between two semi-infinite dielectrics media have been studied in both visible and microwave spectral bands with the appropiate LHM and appropiate location of LANS in the structure. The frequency dependence of  and
and 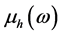 of LHM and that of LANS is taken into account. It has been shown that, the frequency-dependent refractive index of both LHM and LANS plays an important role in the variation of the reflection coefficients of the structure. Low reflection can be achieved for both visible and microwave rays by choosing the proper indicies of the materials constiuted the structure. For incident visible rays, LANS is located as shown in Figure 1 r = 0 and then T = 1 is attained at a sigle wavelength value of 600 nm with magnetic fraction of LANS of value 0.9, incidence angle of value 0˚ or 27˚. For incident microwave rays, LANS is located in Region 1 and the dielectric in Region 3. r = 0 and then T = 1 are achieved at wavelength
of LHM and that of LANS is taken into account. It has been shown that, the frequency-dependent refractive index of both LHM and LANS plays an important role in the variation of the reflection coefficients of the structure. Low reflection can be achieved for both visible and microwave rays by choosing the proper indicies of the materials constiuted the structure. For incident visible rays, LANS is located as shown in Figure 1 r = 0 and then T = 1 is attained at a sigle wavelength value of 600 nm with magnetic fraction of LANS of value 0.9, incidence angle of value 0˚ or 27˚. For incident microwave rays, LANS is located in Region 1 and the dielectric in Region 3. r = 0 and then T = 1 are achieved at wavelength
 (a)
(a) (b)
(b)
Figure 5. (a) The reflected, (b) transmitted power versus the layer thickness d at normal incident wavelength of λ = 600 nm, 800 nm, nd =4.86, f1 = 0.7.
 (a)
(a) (b)
(b)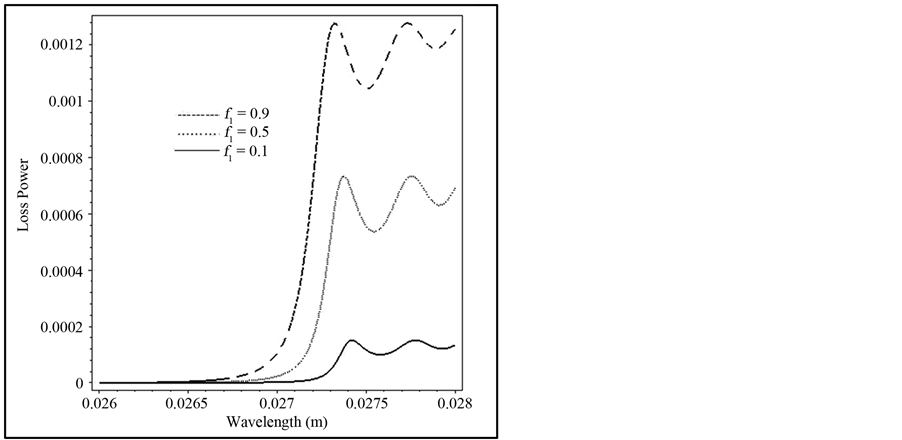 (c)
(c)
Figure 6. (a) The reflected, (b) transmitted, (c) loss power versus the incident wavelength when the magnetic fraction f1 changes as f1 = 0.1, 0.5, 0.9, nd = 4.86, θ = 30˚, d = 14 mm, γe = γm =0.1.
λ = 0.026 to 0.272 m with f1 = 0.1 at θ = 30˚. The implementation of LANS adjacent to LHM layer dramatically reduces the reflection and greatly enhances the transmission near a specifically frequency. The law of conservation of energy has been satisfied by the obtained results. The obtained results may be used to refine the understanding of any related applications that may be modeled requiring controlling of reflected and transmitted powers as photovoltaic cells and optoelectronic devices.