1. Introduction
Social networks, such as Facebook and Twitter, have been rapidly growing in recent years. Such a network can be represented as a graph, where a node represents a user and an edge represents their affiliation with others. Figure 1 illustrates this idea. These affiliations can represent friendships or likes, as in Facebook, or followings, as in Twitter. Nodes with similar affiliations tend to group into densely knit communities to form network structures. Moreover, research has discovered three characteristics of social network structure. First, the small world phenomenon can be described as any two nodes that are related to each other through only a small number of other nodes. Second, the power law is the distribution of node degree following the pattern of a power func-

Figure 1. Illustrates a graph with nodes connected to other nodes by edges.
tion. The third is the observed community structures within a network [1] . The fast growth of social networking sites in the past decade has caused a need to analyze its community structures.
A community in a network is a group of nodes that are densely connected inside and sparsely outside. Community detection can reveal information about the users in each community, such as common interests, relationships, or views. Similarities between individuals within a community can be used in advertisements, where one user’s likes can be applicable for the other users within the same community; behavioral trends between individuals of a common community; or even similarities between genes in a genetic sequence.
There is no fixed order or form to network structures, as they arise randomly in different shapes and sizes [1] , leading to difficulties in detecting communities accurately. There are many community detection algorithms in use today, ranging from label propagation [1] to density analysis [2] . Many of these algorithms are designed to discover communities in static networks and do not scale well. Networks today include millions of nodes and billions of edges and are continually changing their structure. Community detection in dynamic networks involves the process of incorporating the community model of a previous timestamp, or snapshot of a network structure, into the detection of the next to improve the efficiency of detecting the new community structure.
Additionally, another aspect about community structure is that many community detection algorithms discover the best possible community membership for each node in the network, but some nodes are too distant from all other nodes and should be considered outliers. Also, there are those nodes that bridge two or more communities, which may or may not be members of the communities they bridge. These bridging nodes are called hubs.
2. Related Work
A general density-based clustering algorithm DBSCAN, Density Based Spatial Clustering of Applications with Noise, was proposed by Ester et al. [3] . DBSCAN forms communities from individual nodes labeled core points. These core points must satisfy a user-defined number of neighbors within a given radius. A node with a neighborhood that is too small is labeled a noise point, unless it falls within the neighborhood of a core point, which then it is labeled a border point. Core points connect to other nearby core points to form the center of a community. Ester et al. [3] devise the means to group these types of densely connected communities.
The SCAN algorithm (Structural Clustering Algorithm for Networks) [2] , derived from DBSCAN, is capable of discovering communities, hubs, and outliers in a network. A community is grown from a group of centralized nodes which all satisfy a given neighborhood size. To define the neighborhood of a node, a user-defined threshold, ε, is introduced. Instead of looking at a node’s immediate neighbors, SCAN uses the ε neighborhood of a node and groups it with those who share a common set of neighbors [2] . A structural similarity measure is used to calculate the similarity between two nodes. Its time complexity is O(n) due to the one time pass through of the set of nodes in the network.
An incremental updating process was described in the DENGRAPH-IO algorithm [4] . This algorithm uses its own variation of DBSCAN, called DENGRAPH, to update the current community structure of a network from a previously detected structure and its changes over time. The changes in nodes and edges are eventually reflected in the edges alone. Incrementally, each edge change, whether added or removed, is incorporated into the previous structure of the network, and an update to the community structure is performed in relation to the edge change. This algorithm defines six possible outcomes that an edge change in the network would cause to a community structure. An added feature to DENGRAPH, compared to SCAN, is that it can discover overlapping communities, by allowing each node to inherit multiple community labels instead of one. Also, to define a density-based neighborhood of a node, DENGRAPH uses the distance between two nodes, while SCAN uses neighborhood similarity.
Similar to community detection by node density is the idea of edge density. This density measures the ratio of the number of inter community edges to the number of intra community edges [1] . Darts et al. introduce the study of edge density in community detection and provided insight into its implementations with other community detection approaches [5] . They introduced the density measure of actual number of edges divided by the possible number of edges, where a community absorbs nodes that allow a specified edge density threshold to remain satisfied.
A common benchmark algorithm used in many comparisons is the Label Propagation Algorithm (LPA) [6] . This algorithm starts out with each node having a unique label, or community membership. It progresses through multiple iterations, which consist of each node acquiring the label from each of its neighbors and taking on the label of the majority; in the case of a tie, a label is randomly selected. Iterations are performed until a convergence is discovered or a designated number of iterations is reached.
LPA is a simple and effective algorithm that can only find disjoint communities, with no overlap. So a variation of the LPA algorithm was proposed that helped to incorporate community overlap. SLPA (Speaker—Listener Label Propagation Algorithm) [7] incorporates LPA with the allowance of each node to hold more than one label to discover overlapping communities.
Genetic algorithm (GA) is a technique that imitates the process of gene inheritance, mutation, selection, and crossover to optimize the solution to a problem. For the use of GA with community detection, the genes represent all individual nodes and their corresponding community. To find a gene that satisfies a good community structure of a network, the gene must maximize a given fitness function, such as modularity. In finding this maximized gene, a population is used consisting of multiple genes, each representing a different community structure. A user-defined number of iterations is performed over the population which mutates each gene into a cross between two or more genes that produce the highest values due to the fitness function. At the end of the iterations, the gene with the highest value from the fitness function is used as the final community structure. More on the use of genetic algorithms in networks can be read at [8] .
3. Density Based Community Detection
Ester et al. [3] , in their formulation of the DBSCAN algorithm, proposed definitions on how to relate nodes to one another in a density-based structure. Density-based community detection is defined where each node in a community share a greater number of connections with each other than with those outside. Let G = {V, E} be the network graph, where V is the set of nodes and E is the set of edges. Also let N(v), where v∈ V, be the set of neighbors of node v, including v, and let E(v) be the set of all edges incident to v. There are several definitions that must be covered to describe the structure of communities in a density-based network. Figure 2 illustrates these points.
3.1. Epsilon-Neighborhood of Nodes
The use of a node’s neighbor is insufficient to define a densely connected community, because a densely connected community must have a high similarity with neighbors in its own community. So to handle these more closely related neighbors, the idea of an ε-neighborhood was formulated.
In DBSCAN, Ester et al. [3] uses a distance function to relate the closeness between two nodes. Their ε-neighborhood incorporated all neighbors that meet a user-defined threshold ε. Given any two nodes u and v:


Figure 2. Shows the definitions of density structure. Node z is shown with its ε-neighborhood, v is directly reachable from w, u is structurally reachable from w, and u and v are structurally connected. The single yellow node is a hub node between the two communities and the red node is an outlier.
SCAN takes a different approach when relating nodes closeness. They define a similarity function that finds a ratio between the number of neighbors they both share in common to the number of neighbors that they each have:
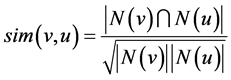
The more neighbors they both have in common, the greater their similarity will be; in the range of (0, 1). So Xu et al. uses a slightly modified version of the ε-neighborhood definition:

3.2. Core Nodes
A node that is considered a core node is one that contains an ε-neighborhood that has a size that satisfies a user-defined threshold of m nodes: |ε-Nei(v)| ≥ m. According to Xu et al., a m of 2 is recommended for analysis.
3.3. Direct Structure Reachability
A node u is directly reachable from node v, if v is a core node and u is in the epsilon-neighborhood of v:
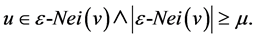
3.4. Structure Reachability
A node u is structurally reachable from node v if there is a chain of nodes that are all directly reachable from the previous until u is reached. This is only capable if the chain of nodes are core nodes, seen by the definition of directly reachable: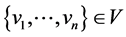 ;
;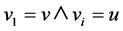 ;
;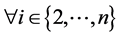 : Directly Reachable (vi-1, vi).
: Directly Reachable (vi-1, vi).
3.5. Structural Connectivity
Two nodes (v, u) are structurally connected if there exists a node x from which v and u are structurally reachable. The two nodes, in this case, can be border nodes, and the node that connects them is a core: ; Structure Reachable(x, v) ⋀ Structure Reachable(x, u).
; Structure Reachable(x, v) ⋀ Structure Reachable(x, u).
3.6. Hubs and Outliers
By SCAN, a node v is a hub node if it does not belong to any community, but it does have more than two neighbors belonging to different communities: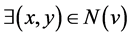 ; x ≠ y ⋀ Community(x) ≠ Community(y).
; x ≠ y ⋀ Community(x) ≠ Community(y).
A node v is an outlier if it does not belong to any community, and it does not contain more than one neigh- boring node that belongs to different communities: ~ ; x ≠ y ⋀ Community(x) ≠ Community(y).
; x ≠ y ⋀ Community(x) ≠ Community(y).
4. Community Structure Reformation Due to Network Changes
In this section, we will introduce the process of updating a dynamic network and the six scenarios that may arise.
4.1. Updating Similarity Value Between Nodes
A change in the structure of a network, such as an edge being added or removed, would affect the similarities between the two nodes that are incident to this edge. Instead of checking the similarity of all edges in the network, only those edges that are related to these two nodes need to be updated. Edge similarities to recalculate due to an edge change of nodes v and u are .
.
4.2. Effects of a Network Change
Falkowski [4] introduces six possible outcomes that a change in a network would produce. Each of these six scenarios is split into two groups by how that changes the community structure. There is the idea of a positive change, where a change will create a new community, a community will receive a new member, or two communities merge. Then there is a negative change, which could remove a community, remove a member from a community, or split a community into two [4] . These two groups with three scenarios within are the fundamental ideas for updating a dynamic network.
Within a positive change, a creation of a community, an addition to a community or a merge of two communities may occur. A creation of a new community would result when nodes become cores and have no ε-neighbors that were cores previously; these new core nodes would establish a new community with its ε-neighborhood. An addition to a community will occur when a node, which previously had not belonged to a community, obtains a similarity with a core that is greater than ε, thus it now belongs to the community of this core. Then a merging of two communities will happen when a core of one community obtains a similarity with a core of another community that is greater than ε, and then the communities of these cores will become one.
In a negative change, a split of a community, removal from a community, or removal of a community may occur. A split will occur when a node, that was once a core, now is no longer a core, and it creates a gap between the other cores of the community. This gap will create a division between two or more chains of cores causing each chain of cores to form separate communities. A removal from a community occurs when a node no longer has a strong connection, or high enough similarity, to a core of its community and is no longer labeled as a member of that community. A removal of a community happens when all cores of a community are reduced from their core status and the community is removed.
To determine whether a change will produce a positive or negative change to a network is not an easy task. Any change in a network will involve an addition or removal of an edge. Then by these two principles, [4] relates the two groups of scenarios with edge changes as: a new edge produces a positive scenario, and the removal of an edge produces a negative scenario. This idea may work for the distance-based approach for Falkowski, but according to our trials on a similarity based approach; this is not always the case. The next section illustrates our algorithm, which handles the edge changes of a network.
5. DSCAN: Improvements to SCAN
Our study is based on the algorithm SCAN [2] and applies improvements to its density based detection. Our modifications to SCAN allow it to form communities without the user-defined threshold of epsilon and can update a dynamic network of timestamps. We propose the algorithm DSCAN (Dynamic SCAN), which can handle these dynamic networks.
SCAN’s threshold of ε, in the range of (0, 1), defines the minimum similarity between two adjacent nodes that must exist for the two nodes to be ε neighbors. This ε-neighborhood is what defines the community structure. Having to rely on user specifications for ε can decrease performance if an incorrect ε is used, and performing multiple runs with different epsilons is costly. In our research with testing various networks, we have discovered that possible good epsilons for any network fall in the range of (0.4, 0.8). An ε too low will produce few large communities, while a larger ε will result many small communities. For our study, to calculate the ε-neighborhood of a node, we perform a check ε the range (0.4, 0.8) and take an average of those results. This approach produces comparable results and alleviates the need to run multiple times to check all ε values. Xu et al. found a good value of μ to be 2, which is the value that we have also used.
Algorithm 1 illustrates the dynamic updating of a network with DSCAN. Given a sequence of timestamps of a network, perform SCAN on the first timestamp. Then for all consecutive timestamps, obtain the difference in edges between the two timestamps. The network is updated from the nodes of each edge change of the networks, illustrated in Method 1. This update on the network handles a node that either becomes a core or was a core and now no longer is. When a change in the network is detected and needs to be updated, an existing cluster id or a new cluster id is propagated through all structurally connected nodes to form a new community. Method 2 explains the propagation of an id through this new community. One final change to the network is when a node no longer belongs to the cluster. Method 3 shows how to handle these nodes and make them either a hub or an outlier.