Gibbs-Donnan Potential as a Tool for Membrane Vesicles Polarization ()
1. Introduction
Membrane potential is a usual characteristic of all the living cells. It is created by ion gradient across the lipid bilayer and reaches values in range −90 ... −50 mV in the state of rest [1] -[4] depending on the cell type. Due to changes in magnitude of membrane potential, cells are able to transmit nerve pulses [5] [6] , couple excita- tion-contraction [7] , communicate [8] , proliferate [9] , and fertilize [10] . Goldman-Hodgkin-Katz voltage equa- tion can be used to calculate value of transmembrane potential (1):
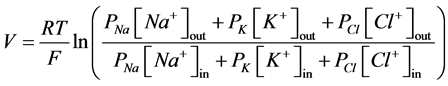 , (1)
, (1)
A simplified formula is used if the only one ion is permeable (K+ for example) (2):
 , (2)
, (2)
Change of membrane potential value can lead to changes in properties of transmembrane proteins (e.g., change in mobility of membrane component affects protein function [11] ) both in eukaryotic and prokaryotic cells [12] [13] . The most popular methods of using membrane vesicle include determining properties of mem- brane protein, characterization of transport system [14] - [21] , study of substrate transport and transporter drug binding kinetics, assign phase behavior of lipid mixtures in bilayers [22] [23] . It should be emphasized that all these processes are sensible to changes of membrane potential. Especially membrane transport and its kinetic parameters, e.g., rates of reactions involving translocation of charged species across the membrane [24] and binding to the membrane [25] , are influenced by membrane potential. In majority of works, polarization of membrane vesicles is achieved by ion gradients in the presence of ionophores as valinomycin-generated K+ dif- fusion potential [14] [16] - [20] . Such methods allow creation of unstable potential with decreasing or dissipating value. Thus, using potassium-valinomycin system provides sufficient but unstable potential that fully disappears in 3 - 5 minutes [26] .
The aim of this work was to find a tool for creating stable and sufficient value of transmembrane potential in membrane vesicles.
2. Methods
Plasma membrane vesicles of smooth muscle cell were prepared from swine myometrium as was described pre- viously [27] . Finally, membrane fraction was resuspended in medium that contain 300 mM KCl.
Protein quantity content in membrane fraction was determined by Bradford method [28] .
Transmembrane potential was measured by potential-sensitive fluorescent dyes and all fluorescent experi- ments were carried out in PTI spectrophotometer. To measure positive-inside membrane potential potential- sensitive dye DiOC6(3) (3,3’-Dihexyloxacarbocyanine Iodide) with final concentration 2.5 µM was used. The excitation wavelength was set to 452 nm (slit width 5 nm) and emission to 506 nm (slit width 5 nm). After the fluorescence signal was constant the aliquot of plasma membrane vesicle (66 µg) was added. Fluorescence changes was measured as coefficient τ = Fv/Fbase, where Fbase—fluorescence signal prior to membrane vesicle addition, Fv—florescence signal after membrane vesicle addition.
To measure negative-inside membrane spectrum shift of potential-sensitive dye oxonol VI was used. It final concentration was 1 µM, protein content was 200 µg/ml.
Results were analyzed by Wilcoxon signed-rank test, p < 0.01 (MS Excel).
Reagents used were as follows: DiOC6(3), Hepes, sucrose (Sigma, USA); Tris-hydroxymethyl-aminomethane (Reanal, Hungary); oxonol VI (Fluka, Switzerland). Other reagents were of domestic production of analytical and chemical purity.
3. Results
3.1. Calculations of Gibbs-Donnan transmembrane potential on membrane vesicle
Gibbs-Donnan equilibrium [29] is conceived when there are two compartments separated by half-permeable membrane and there are impermeable ions in one of the compartments and permeable salt in both ones. But ob- tained value of Donnan potential is not high, only about ±11 mV. However, earlier Prof. Kosterin predicted [30] that Donnan effect can be used for creation of stable, equilibrium membrane potential if compartments volumes significantly differ (3).
 (3)
(3)
where we and wi summary volume of each compartments. This work continues his studies.
In calculations electrochemical system contains two compartments which divided by half-permeable mem- brane. In one of the compartment there permeable salt, which is potassium chloride (b)—KCl, because it is one of the most ubiquitous ion in organism. At the beginning of our study we did not know what is better to use: salt of impermeable anion with potassium (x)—KA, or cation with chloride (z)—CatCl, and where it is better to be placed—inside (lower index i) or outside the vesicle (lower index e). So general formula and four special cases (Figure 1) of it was reviewed:
A) Impermeable anion inside vesicles.
B) Impermeable cation inside vesicles.
C) Impermeable anion outside vesicles.
D) Impermeable cation outside vesicles.
In calculation it is important to maintain condition for initial isotonicity (4):
 , (4)
, (4)
where b0,i—initial concentration of KCl inside vesicles, z0,i—initial concentration of CatCl inside vesicles, x0,i— initial concentration of KA inside vesicles, b0,e—initial concentration of KCl in incubation medium, z0,e—initial concentration of CatCl in incubation medium, x0,e—initial concentration of KA in incubation medium. Accord- ing to this sum over all the salts concentrations must be the same in two compartments. This principle is in- volved by the fact that osmotic power in two compartments should be equal.
To diverse general formula of Gibbs-Donnan potential several principles are used as input data.
1) Particles balance (5) (6). It describes particles balance before and after equilibrium between incubation me- dium (we) and vesicles (wi) and considering equality of salt and ions concentration.
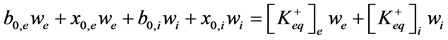 , (5)
, (5)
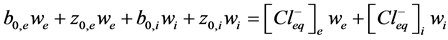 , (6)
, (6)
where ,
, 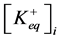 —concentration of potassium ions in equilibrium point in incubation medium and ve-
—concentration of potassium ions in equilibrium point in incubation medium and ve-
sicles correspondingly, 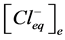 ,
,  —concentration of chloride ions in equilibrium point in incubation
—concentration of chloride ions in equilibrium point in incubation
medium and vesicles correspondingly.
2) Equality of electrochemical potentials (μ) in Equilibrium (7)-(12). Electrochemical potential created by every ion inside of vesicle is equal to potential formed on the external side of membrane.
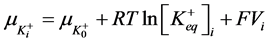 , (7)
, (7)
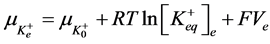 , (8)
, (8)
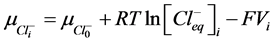 , (9)
, (9)
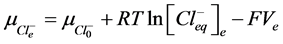 , (10)
, (10)
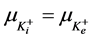 , (11)
, (11)
 , (12)
, (12)
3) Electrical neutrality (13) (14), which describes balance of positive and negative charge in each side of membrane:
![]() , (13)
, (13)
![]() (14)
(14)
Considering three principles mentioned above (4)-(14) and the calculation transmembrane potential equation (2), taking into account compartments size, a general formula for calculating transmembrane potentials caused by Gibbs-Donnan effect was obtained (14).
![]() , (15)
, (15)
where ![]() .
.
As it was predicted by Kosterin [30] , the higher difference between compartment volumes is, the higher Donnan potential can emerge. To validate this assumption, dependence of transmembrane potential on value of θ was visualized (Figure 2).
![]()
Figure 1. Gibbs-Donnan effect in polarization of membrane vesicle. There are four cases differing in impermeable ion charge and location. (a) There is potassium chloride in the medium and there are potassium chloride and salt of potassium with impermeable anion inside the vesicle. Concentrations of potassium chloride in the medium and sum of potassium chloride and potassium anion concentrations in vesicle are equal, in other words [KCl]I = [KCl]e + [KA]e. Since concen- tration of chloride ions in medium is higher, due to the concentration gradient chloride ions move into the vesicle. At the same time concentration of impermeable anions inside vesicle is higher than in medium, but membrane is not permeable for it, so anions cannot move outside vesicle. Taking all the points into account additional negative charge inside the vesicles is created. (b) There is potassium chloride in medium and there are potassium chloride and salt of impermeable cation with chloride inside vesicle. Concentrations of potassium chloride in medium and sum of potassium chloride and cation chloride concentrations in vesicle are equal, that means [KCl]I = [KCl]e + [CatCl]e. Due to the concentration gradient potassium ions move into the vesicle. Like in (a) concentration of impermeable ion inside vesicle is higher than in medium, but membrane is not permeable for it, so cations stay inside. Thus, additional positive charge inside the vesicles is created. (c) There is potassium chloride in vesicles and there are potassium chloride and salt of impermeable anion with potassium in medium. Concentrations of potassium chloride in vesicles and sum of potassium chloride and potassium anion concentrations in medium are equal, so [KCl]I + [KA]I = [KCl]e. Due to the concentration gradient chloride ions move out from the vesicles, and impermeable anions stay in medium because membrane is not permeable for them. Additional negative charge outside the vesicles is created. (d) There is potassium chloride in vesicles and there are potassium chloride and salt of impermeable cation with chloride concentrations in medium. Salts concentration must fit the following equation: [KCl]I + [CatCl]I = [KCl]e. Due to the concentration gradient potassium ions move out from the vesicles, and impermeable cations stay in medium because membrane is not permeable for them. Additional positive charge outside the vesicles is created.
![]()
Figure 2. Theoretically calculated increase of transmembrane Donnan poten- tial depending on internal/external compartment size ratio (θ). Some random salt concentrations were used.
From the Figure 2, it is clear that the lower θ is, the higher Donnan potential can be formed. It is known that size of vesicle is quite small, about 0.3 - 0.4 µm, which is confirmed in our laboratory by electron microscopy and hydrodynamic diameter measurement (data is not shown). Medium volume is two or three order of magni- tude as big as the sum over all the vesicle volumes, which means that volumes of compartments significantly differ as (3), thus, ![]() , so that expression 15 is simplified to (16):
, so that expression 15 is simplified to (16):
![]() . (16)
. (16)
It was mentioned that there are four cases depending on location and charge of impermeable ion. First one is when anions are located inside vesicle, in other words, in smaller compartment (Figure 1(a)). Due to the Don- nan effect negative charge appears inside vesicle. We considered it as a positive transmembrane potential, in other words, transmembrane potential is positive if internal side of membrane has bigger negative charge than external side has.
So when x0,e, z0,e, z0,i = 0, the value of Donnan potential can be obtained from the simplified Equations (16).
![]() . (17)
. (17)
So dependence of membrane potential on impermeable anion concentration was obtained (Figure 3).
Figure 3 shows that the higher concentration of impermeable salt is used the higher Donnan potential can emerge. Nevertheless value of it is insufficient for further investigation, because value of live cells transmem- brane potential is 6 times as big as the value that may be obtained. In real experimental conditions overall salt concentration higher than 0.3 mM cannot be used because it is far from real osmotic power in the tissue or cell.
Such a result is quite similar to what appears in the second case, whereas salt of impermeable cation is located inside vesicle (data is not shown) and x0,i, x0,e, z0,e = 0. There is only one difference—the charge inside the ve- sicles is opposite. Hence location of impermeable ions regardless to its charge cannot provide sufficient value of transmembrane potential. Yet there are two others cases, where impermeable ions are located in medium, in other words in a compartment which volume is much higher.
In third case, impermeable anions are located in medium, outside the vesicles (Figure 1(c)). The value of Donnan potential in conditions when x0,i, z0,i, z0,e=0 can be obtained from a quite simple formula (18):
![]() . (18)
. (18)
![]()
Figure 3. Calculations of influence of concentration salt of impermeable anion on the value of Donnan potential (ED) in case when initially salt of impermeable anion (x0,i) is located inside vesicle. Salts concentrations satisfy such demand x0,i + b0,i = b0,e = 300 mM.
Dependence of transmembrane potential on impermeable salt is like in the previous cases, the higher concen- tration is, the higher potential is. However, value of Donnan potential is higher comparing to cases where im- permeable ions are inside vesicle (Figure 4). Its value fits range observed in real cells, thus, it can be used as a tool in experiments for membrane polarization.
Both results with impermeable ions inside vesicles and results with ions in medium are quite similar (Figure 5) and have one difference—charge of polarization. In four case dependence on salt concentration in conditions when x0,e, x0,i, z0,i = 0 also resembles previous (19):
![]() . (19)
. (19)
3.2. Positive potential on vesicle Is proven by changing of DiOC6(3) fluorescence level
This dye was used for checking the polarization existence in case when in medium there is impermeable cation salt present. Due to our calculations negative charge should be accumulated inside vesicle (Figure 1(d), Figure 5). According to literature data the fluorescent signal of DiOC6(3) is drop if hyperpolarization occur and rise during depolarization [31] , thus in this case of vesicle polarization fluorescence signal should decrease.
As a control experiment the medium which contained only 300 mM KCl was used. In a sample probe medium contained 297 mM cholin chloride and 3 mM KCl (as some amount of it added with membrane vesicle aliquot). According to our calculation in such conditions transmembrane potential about −65 mV should appear.
When dye added to medium there was an initial period of slow decline in light emission. Vesicle was not added until a steady level was reached (about 5 minute). After vesicle addition rapid signal increase was ob- served, which level was stable during at least 10 minutes. Finally, SDS 0.005% was used and both signal as in control, so in sample reached one level of florescence (Figure 6).
Thus, Gibbs-Donnan potential is stable in time. Additional experiments show that equilibrium potential is sta- ble during at least 10 minutes.
To compare fluorescent signal in probe and control often base level of dye fluorescence was differ, so coeffi- cient τ was used (τ = Fv/Fbase, where Fbase—fluorescence signal prior to membrane vesicle addition, Fv—fluo- rescence signal after membrane vesicle addition). In Figure 7, there is comparison of average meaning of τ in con-
![]()
Figure 4. Calculated Donnan potential (ED) increase in membrane vesicles depending on salt concentration of impermeable anion (x0,e) initially located in medium. Salts concentrations satisfy such demand b0,i = b0,e + x0,e = 300 mM.
![]()
Figure 5. Calculated Donnan potential (ED) increase in membrane vesicles depending on salt concentration of impermeable cation (z0,e) initially located in medium. Salts concentrations satisfy such demand b0,i = b0,e + z0,e = 300 mM.
trol (2.71) and probe (1.74) experiment, which are statistically different (n = 15, p < 0.01).
Our results convincingly show that Gibbs-Donnan equilibrium can be used for formation of transmembrane potential in vesicle-like structure. However, the majority of vesicle during preparation is formed as “inside-out” structure and following experiment use vesicle for accumulation of ion, metabolites also of “inside-out” confi- guration. To simulate transmembrane potential of cell on membrane “inside-out” vesicle potential with negative charge should be created, in other word impermeable anion should be placed in incubation medium.
![]()
Figure 6. Dependence of fluorescent signal of potential-sensitive dye DiOC6(3) on plasma membrane vesicles potential: control (1)—medium contained 300 mM KCl, estimated poten- tial is 0 mV, probe (2)—medium contain 297 mM cholin chloride and 3 mM KCl, estimated potential is −65 mV. KCl concentration in vesicle was 300 mM. The result of typical ex- periment is shown.
![]()
Figure 7. Comparison of fluorescent signal coefficient of potential-sensitive dye DiOC6(3) for control (medium contain 300 mM KCl) and probe (297 mM cholin chloride and 3 mM KCl) measured on membrane vesicle (n = 15, p < 0.01).
3.3. Negative potential on vesicle Is proven by oxonol VI spectrum shift
According to literature data [32] oxonol VI have red-shift its absorbtion and emission peak when interact with liposomes and have a great red-shift if liposomes have inside-positive membrane potential.
In our results, oxonol VI also had red-shifted peak of absorbtion and emission (Figure 8, Figure 9), when ve- sicle was added, from 590 to 593 in absorption and from 620 to 623 in emission. However great shift from 590 to 602 ± 1 nm in absorption and from 620 to 632 ± 1 (n = 6) in emission was when vesicle was polarized (n = 6) as a
![]()
Figure 8. Changing exitation spectrum of oxonol VI after adding membrane vesicles (2) and polarized plasma membrane vesicles (3) comparetively with control in icubation medium (1). The result of typical experiment is shown (n = 6).
![]()
Figure 9. Changing emission spectrum of oxonol VI after adding membrane vesicles (2) and polarized plasma membrane vesicles (3) comparetively with control in icubation medium (1). The result of typical experiment is shown (n = 6).
result of Gibbs-Donnan effect. Control experiment as in previous case was performed in incubation medium which contained 300 mM KCl and 200 µg vesicles, which contained also 300 mM KCl. Sample probe contained 297 potassium citrate (as impermeable anion) and 3 mM KCl with vesicle of the same composition.
4. Conclusions
The influence of Donnan effect on membrane polarization when size of one compartment is very different from another has been reviewed in this research.
It should be emphasized that location of impermeable ion influences on the value of transmembrane potential that will be obtained. Impermeable ions location in incubation medium creates transmembrane potential 6 times as high as location of corresponding ions in membrane vesicles. It can be explained by the different particles number. However, salt concentration is equal but compartment volumes are significantly different, that means various numbers of available particles and load limit in each compartment. Concentration gradient directed out from the smaller compartment is better for higher polarization, as its load limit in equilibrium point is relatively low.
Therefore, location of impermeable ion in incubation medium creates stable Donnan potential which depends on 1) concentration of ion: the higher concentration is the higher membrane potential can be created; 2) charge of ion: impermeable anion creates a negative transmembrane potential and cation forms a positive transmem- brane potential. Different sign of polarization can be used for studying depolarization-hyperpolarization event during cell excitation.
Theoretical calculations were confirmed via using two different potential-sensitive probes in diverse incu- bation medium. It was expected that when impermeable cation (in this case choline) located in medium and vesicle contain equivalent concentration of permeable cation (potassium) positive transmembrane potential should be formed. This was confirmed by different fluorescence quantum yield of potential-sensitive probe DiOC6(3). In other case oxonol VI was used for verifying vesicle polarization where impermeable anion (citrate) placed in medium and vesicle was fulled by tantamount concentration of permeable anion (chloride). The shift of spectrum of specified probe in emission and excitation spectrum was noted in this case and according to Apell [32] testifies membrane vesicle polarization.
Thereby, Gibbs-Donnan effect can be used in vesicular method of investigation in order to form stable trans- membrane potential. In further investigation stable transmembrane potential in membrane vesicles can be used for analysis electrical-sensitivity of transmembrane ion transporters, for example, the plasma membrane Mg2+, ATP-dependent Ca2+-pump.