Compatibility of Quantum Entanglement with the Special Theory of Relativity ()
1. Introduction
The Einstein-Podolsky-Rosen paradox [1] stating that quantum mechanics is incomplete because it violates local realism is resolved by Bell’s theorem [2] , in which Bell’s inequality is violated by quantum mechanics as demonstrated experimentally by Freedman and Clauser [3] . A less abstract way of saying this is the following: although the deterministic description of causality as stated in Einstein’s special theory of relativity is violated, nevertheless causality cannot be violated by a physically correct quantum theory of electrons in which local realism is not observed due to the quantum nature of the motion. Such a physically correct theory is the quantum theory of a relativistic electron by Dirac [4] in which the principles of special relativity are incorporated in an equation of motion for a spin-1/2 particle. This statement must be true but yet there is a vagueness or highly abstract character to our understanding of quantum entanglement even after it has been sorted out by the Bell-Freedman-Clauser work. This abstract character, which likely underlies the early perplexity of Einstein, Schroedinger, and others concerning entangled states, exists for two reasons. First electron-electron correlation is not understood in a dynamical sense. We know that two electrons must correlate in space and time, but correlation is understood using time-independent or stationary-state quantum theory both nonrelativistically and relativistically. Second electron spin plays a fundamental role in quantum entanglement, but yet quantum entanglement is understood using Schroedinger theory, in which the electron’s spin degree of freedom is absent. In practical calculations the omission of spin in the equation describing electrons and their mutual interaction means that the quantum states for two or more electrons must be constructed empirically from experimental observation of how an aggregate of electrons behaves. In other words, there is no mathematical prescription in the many-electron Schroedinger equation itself for Fermi-Dirac statistics, and in fact in many-fermion numerical simulations, ad hoc procedures must be used to avert what is called bosonic collapse of the solution. Thus, a physically correct many-electron wave function must be constructed to obey the Pauli Exclusion Principle and Fermi-Dirac statistics. It is well known that a physically correct many-electron wave function in orbital and spin space must be antisymmetric with respect to electron exchange, which is a mathematical recipe to guarantee the Pauli Exclusion Principle and to reconstruct the dynamical information which is otherwise lost in stationary-state theory. The Pauli Exclusion Principle and Fermi-Dirac statistics have only recently been demonstrated on an ab initio basis using a dynamical quantum theory of electron exchange-correlation in space and time [5] [6] . In this paper, I show that the previous work [5] [6] also provides an understanding in a dynamical sense of quantum entanglement and disentanglement.
2. Dynamical Theory of Quantum Entanglement
The Pauli exclusion principle, which is fundamental for fermion structure and collision problems, states that each fermion in an ensemble must have a unique set of four quantum numbers three for space and one for spin. For example a pair of electrons can occupy the same spatial orbital only if they have opposite spin states. The canonical examples are the singlet and triplet states (for upper and lower signs respectively) of the helium atom or of the hydrogen molecule,
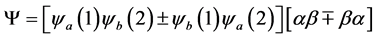 , (1)
, (1)
where the arguments refer to the 3-space position vectors of electrons 1 and 2. The second term in square brackets comprises up (alpha) and down (beta) spin states such that the 2-electron spin state is 0 (singlet state) or 1 (triplet state) for upper and lower signs respectively. This point is obvious if the orbitals labeled a and b are identical such that fermions 1 and 2 occupy the same spatial orbital for the singlet state (upper sign) while the first term in square bracket vanishes for the triplet state (lower sign) since the Pauli exclusion principle is violated for this case.
The singlet state is a canonical example of an entangled state since the two electrons cannot be separated spatially and appear therefore to transfer information between themselves instantaneously. In a way the mysterious nature of the entangled state is illusory due to the incompleteness of the physical theory itself. Firstly the theory is for stationary states with no dynamical information whatsoever between the two correlated electrons. Second Schroedinger theory is spinless such that the 2-electron state written in Equation (1) is an ad hoc construction based on experimental observation. It is true that the symmetry of the Schroedinger Hamiltonian with respect to the permutation of electron coordinates allows for pairs of spatial states in the first square bracket to have either even (upper sign) or odd permutation symmetry on the exchange of electrons. Nevertheless the spin dependence of the 2-electron wave function has a totally phenomenological origin such that no a priori physical theory exists to explain why the state with total spin angular momentum of 0 is an entangled state while the state with total spin angular momentum of 1 is an unentangled state.
Ironically the paradox is resolved by Einstein’s own theory of special relativity. Dirac discovered the correct quantum theory of special relativity for a fermion, which makes it possible to explain both the explicit dynamical nature of entanglement and its dependence on the spin state of a fermion. Figure 1 and Figure 2 show 2-electron entanglement and nonentanglement for singlet and triplet states respectively.
The form of Dirac theory which makes this detailed understanding possible is outlined below. First I postulate that a correct dynamical theory for a relativistic electron interacting with other relativistic electrons can be had by replacing the classical relativistic equation of motion for each electron by Dirac’s equation as follows [5] [6] .
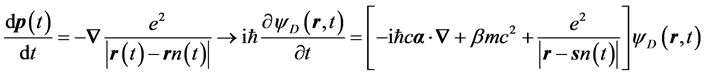 (2)
(2)
where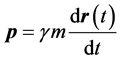 ,
, 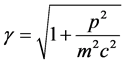 ,
, 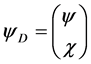 ,
, 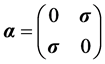 , and
, and 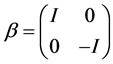 for Pauli’s spin vector
for Pauli’s spin vector 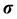 and the 2 × 2 identity matrix I. The generalization to many electrons is obvious. For example for any two
and the 2 × 2 identity matrix I. The generalization to many electrons is obvious. For example for any two
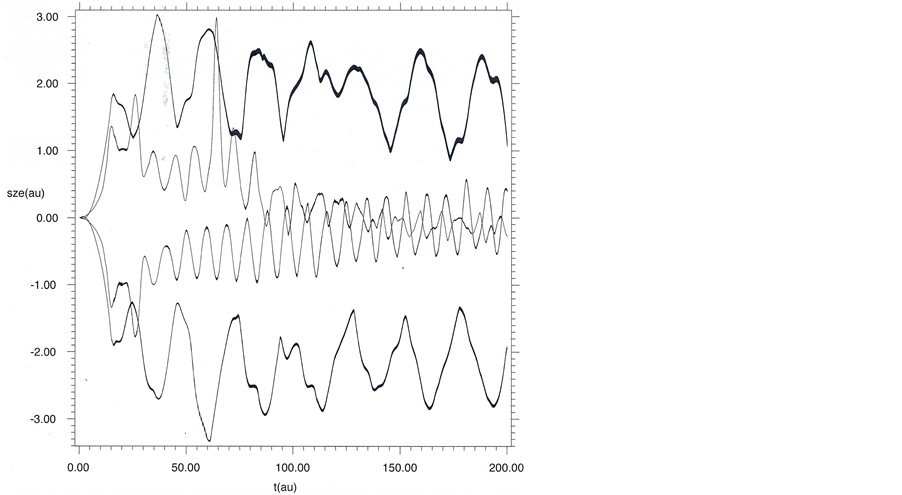
Figure 1. Quantum eigentrajectories in the z direction. Inner curves: R = 1.4 au (R is the internuclear distance). Outer curves: R = 3.0 au. The inner curves show how two electrons with opposite spin states correlate and entangle with increasing time and eventually find the region of covalent bonding located between the two protons fixed at 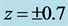 au, while the outer curves show that the electrons remain in the vicinity of the separated atoms for all times. The eigentrajectories are calculated from Equation (5) in the nonrelativistic limit using eigenfunctions for the up and down spin states for the
au, while the outer curves show that the electrons remain in the vicinity of the separated atoms for all times. The eigentrajectories are calculated from Equation (5) in the nonrelativistic limit using eigenfunctions for the up and down spin states for the 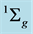 state of H2.
state of H2.
electrons equations of motion analogous to Equation (2) would be written for the primed-variable electron whose interaction with the other electron would now be expressed using the unprimed variable. Notice the passage from classical to quantum dynamics of Coulomb’s Law 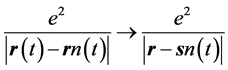 for the interaction of any two electrons whose trajectories are at
for the interaction of any two electrons whose trajectories are at 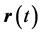 and
and 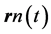 classically and at
classically and at 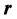 and
and 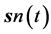 quantum mechanically.
quantum mechanically.
The quantum trajectory is calculated for the unprimed-variable electron as follows. First this electron’s velocity field 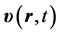 is inferred from its current,
is inferred from its current,
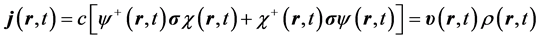 , (3)
, (3)
where 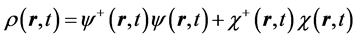 and from which a trajectory,
and from which a trajectory,  , can be calculated from the time integration of the velocity field to find a position field,
, can be calculated from the time integration of the velocity field to find a position field,
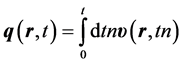 , (4)
, (4)
and finally by finding the quantum expectation value of the position field,
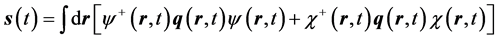 (5)
(5)
and similarly for the primed electron.
In the nonrelativistic regime of electron velocity the current is evaluated in the nonrelativistic limit using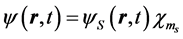 and
and 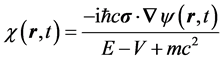 where
where
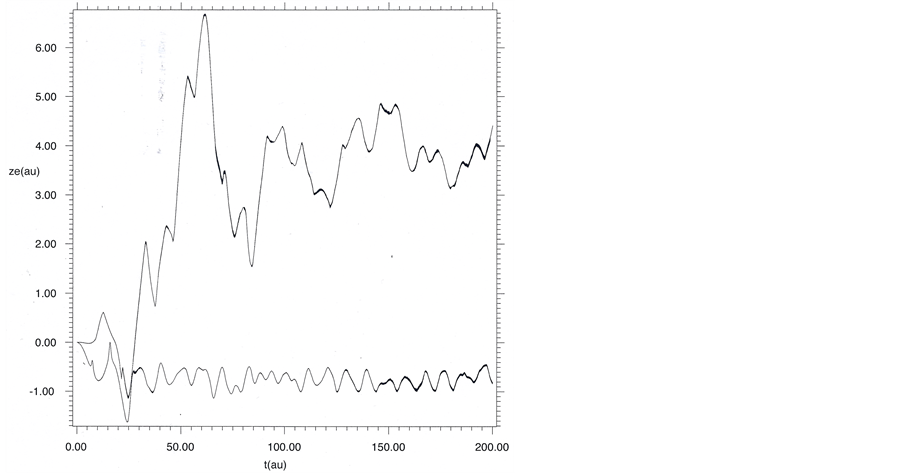
Figure 2. Quantum eigentrajectories showing how the two electrons of H2 correlate but remain unentangled with increasing time in the formation of an antibonding state. Solid: spin-up electron. Dotted: spinup electron. The eigentrajectories are calculated from Equation (5) in the nonrelativistic limit using eigenfunctions for two parallel spin states of the 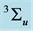 state of H2.
state of H2.
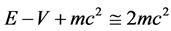 and
and  obeys the time-dependent Schroedinger equation,
obeys the time-dependent Schroedinger equation,
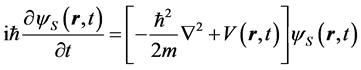 . (6)
. (6)
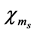 has up (plus sign) or down (minus sign) spin states denoted by
has up (plus sign) or down (minus sign) spin states denoted by 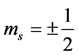 (i.e.
(i.e. 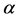 or
or 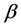 spin states) respectively. Written out explicitly in terms of the large component the current given by Eq. (3) becomes
spin states) respectively. Written out explicitly in terms of the large component the current given by Eq. (3) becomes
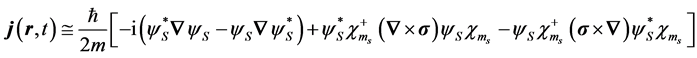 , (7)
, (7)
where we have used 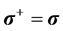 and the identity,
and the identity, 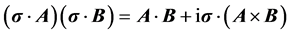
from which the identities useful in evaluating the current can be inferred,
 (8a)
(8a)
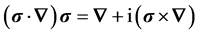 . (8b)
. (8b)
Written out explicitly for up (upper sign) or down (lower sign) spin states The current in the nonrelativistic regime is
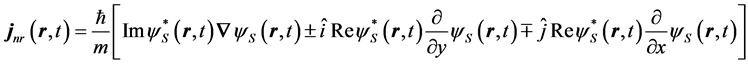 (9)
(9)
The first term on the right side of Equation (9), which is independent of spin, is contributed by Schroedinger theory, while the second and third terms are contributed uniquely by Dirac theory. Notice that the current and therefore a quantum trajectory scale like all of the other Schroedinger contributions, namely as c0 and not as c-2, which have been dropped in the Schroedinger limit of Dirac’s equation. It is found in [1] [2] that Pauli’s exclusion principle is satisfied automatically on using the spin-dependent quantum trajectories given by Equation (9) to calculate the electron-electron Coulomb potential. Hence one may conclude that electron exchange-correlation—it was recognized by the authors of early highly accurate variational calculations [7] that exchange is automatically satisfied when correlation is calculated exactly—and Pauli-Dirac statistics are relativistic effects which persist into the nonrelativistic regime. This is obvious on recognizing that spin is a property of a relativistic electron such that in Schroedinger theory the Pauli principle must be satisfied on an ad hoc basis from phenomenological observation requiring great mathematical labor to simulate the physical link between electron spin and electron correlation which is omitted in Schroedinger’s formulation of quantum theory.
Notice finally that the first-principles understanding of Fermi-Dirac statistics makes available to us a new highly practical computational methodology in which one needs an efficient, accurate solver for the 3D timedependent Schroedinger equation and an efficient, accurate, energy-conserving integrator for the quantum trajectories. Configuration interaction (CI) calculations are obviated since the time-dependent solution is a superposition of ground and excited states. One should not fuss that the electron-electron Coulomb potential has a mixed evaluation using an independent position variable for one electron and a dependent position variable for the other electron: quantum mechanics allows us latitude to calculate the inverse distance between two point particles as long as it is calculated wave mechanically and not deterministically. The mathematical bête noir of conventional time-independent many-electron quantum theory is of course the electron-electron Coulomb potential calculated as an inverse distance using independent position vectors for both electrons. Quantum mechanics does not require us to seek a single wave function for N electrons instead of N wave functions for N electrons, and the former appears to be an accident of the additivity of the Schroedinger Hamiltonian leading to a vast literature on independent-electron approximation methods and on scholastic research on density functionals in which angels are replaced by orbitals. Except for the Bethe-Salpeter equation for two fermions, relativistic invariance is satisfied by a one-body Dirac equation in 4-space: three spatial variables and the scaled time ct. Hence in Dirac theory it is natural to write N wave functions for N fermions as in Equation (2) instead of one wave function for N fermions. As long as the electron-electron potential is written as an exact instantaneous interaction in 3-space and the time, then both electron exchange-correlation and its corollary Fermi-Dirac statistics will be dynamically achieved.
3. Conclusion
In this paper, I have demonstrated quantum entanglement and disentanglement (Figure 1 and Figure 2 respectively) in time and space, thereby removing the abstract understanding of these phenomena based on nonrelativistic stationary-state quantum mechanics. This is achieved by inference of a dynamical theory of the electron correlation from Dirac’s theory for a relativistic electron such that Fermi-Dirac statistics is obeyed on an ab initio basis, thereby elucidating the physical relationship between electron correlation, electron spin, and entangled states.
Acknowledgements
The author is grateful to T. Scott Carman for supporting this work. He is grateful to Professor John Knoblock of the University of Miami for the seminal discussion. This work was performed under the auspices of the Lawrence Livermore National Security, LLC, (LLNS) under Contract No. DE-AC52-07NA27344.