The Features of Acoustic Bathymetry of Sludge in Oil Storage Tanks ()
1. Introduction
Large aboveground storage tanks (AST) are used as reservoirs for the storage of crude oil prior to processing. Typical construction is a steel cylinder (API 650) with a diameter up to 120 m and height up to 20 m. The tank is not pressurised and a pontoon roof with a rim seal floats on the oil surface to minimize the release of hazardous vapours to the atmosphere. When the crude oil is fully drained from the tank the pontoon roof is mechanically supported on evenly distributed leg supports. The height of the legs in the maintenance position is about 2.5 m. Crude oil is a very heterogenous raw material. Depending on the producing oilfield the composition can contain different fractions of water, gravel, sand and heavy asphaltenes, paraffin or wax hydrocarbons. Over time these mixed fractions become deposited on the bottom of the tank as a heavy viscous sludge. This sludge reduces the available tank volume, accelerates corrosion, traps water and may contain pockets of gas or other toxic impurities. On the other hand, the sludge has some value if processed, as it may contain up to 80% of usable hydrocarbons. Tank sludge cleaning is a very costly and time consuming operation, and it is therefore necessary to know not only the amount of sludge in the tank, but the spatial distribution. If in some places the local sludge height exceeds the height of the leg support then there is a risk of damage to the roof when lowered to the maintenance position. Measurement of the volume and its spatial distribution is typically performed manually using a special weighted metal tape measure. The sludge/oil interface is detected by the operator feeling the change in weight of the measurement tape as it makes contact with the higher density sludge surface. Manual measurement is time consuming, subjective and places the operator in a potentially hazardous area for long periods since H2S gas is typically present in crude oil. Manual measurements can be made only in a few entry points so the reliability of the measured volume and character of sludge distribution over the bottom are very poor. The error of the measured volume can be up to 35% - 45%. Note that a measurement error of a few centimeters can lead to an error in sludge volume of several hundred cubic meters.
Currently the most promising method of sludge evaluation in large storage tanks is acoustic profiling. Acoustic profiling is similar to acoustic bathymetry in Oceanography but the technical implementation of suitable devices differs from marine multi-beam echo sounders due to the specific conditions of sound propagation in crude oil and the characteristics of closed tank environments that significantly influence signal processing methods. In this article we will discuss the basic physical effects associated with sound propagation in the crude oil which has a major influence on the reliability of measurements of sludge distribution and the evaluation of its volume.
2. Parameters of Crude Oil
The properties important for acoustics are only well understood for pure refined oils. The acoustic properties of crude cannot be tabulated because of the wide variation of crude oil produced from different oilfields. The most important parameters are sound speed velocity in the crude oil, Ccr, attenuation, αcr and character and level of backscattering echo-signals from the boundary of the “oil-sludge”. In turn, the sound speed depends on the temperature of crude oil, its density, water content and dissolved gas. Sound attenuation is determined by the absorption and additional losses due to sound scattering caused by the dissolved gas, various suspensions and water-oil emulsion layer. Another important fact is that all these parameters can significantly vary both in time and in space, i.e. their distribution can be anisotropic. This in turn causes additional refraction effects of the acoustic rays. Furthermore the oil tank is an enclosed design and its metal walls and different internal metal constructions (roof supports, heaters, mixers, and pipes) perfectly reflect the sound waves. Such reflections are a source of strong reverberation, which has a negative impact on performance.
2.1. Specific Gravity of Crude Oil (Oil Density)
In accordance with the classification of API (American Petroleum Institute) all crude oil is divided into 4 types: the “light”, “medium”, “heavy” and “extra-heavy” [1] . To estimate the density of the oil industry uses specific units API0, which are associated with normal density SG = 
 (1a)
(1a)
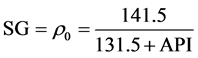 (1b)
(1b)
Light Crude has an API gravity higher than 31.1˚ API, Medium Crude has an API gravity between 22.3˚ API and 31.1˚ API and Heavy Crude has an API gravity below 22.3˚ API. This specification is for T = 16.5˚C. Figure 1 shows plots of the kinematic viscosity of oil versus temperature for different values of the API, the dotted line on these graphs shows the kinematic viscosity of crude versus density at temperature T = 20˚C. Many empirical relations are offered for the calculation of oil density versus temperature. A commonly used formula is:
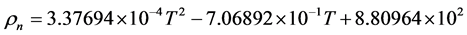 (2)
(2)
2.2. Sound Speed
Numerous measurements of sound speed in crude oil showed that it decreases with increasing temperature. This is opposite to the temperature dependence of sound speed in water. We will not discuss in detail the physical reasons for such behavior of sound speed especially since in the literature there are many often opposing points of view. Researchers have proposed many empirical formulas of which the following is widely used, [3] -[5] :
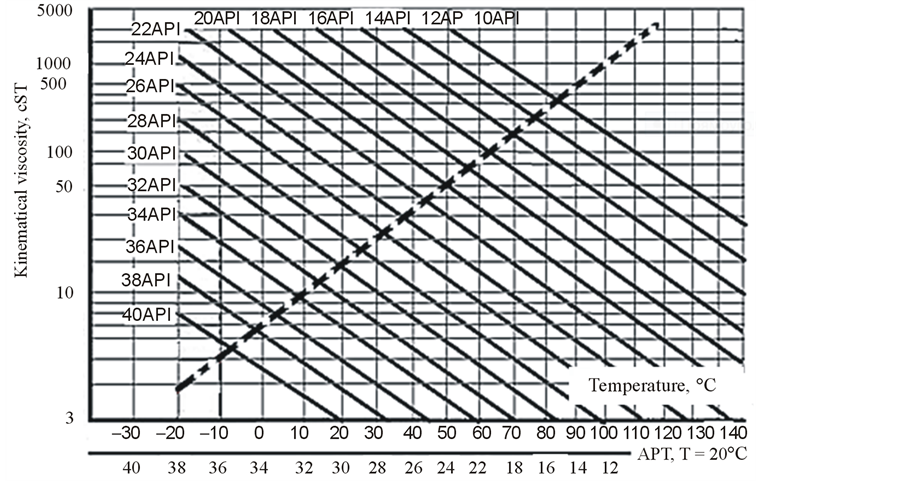
Figure 1. Oil viscosity versus gravity and temperature according ASTM Standard Viscosity Temperature Charts for Liquid Petroleum products (D34), (Courtesy of Paragon Engineering Service, Inc.).
 (3)
(3)
The dependence of the sound velocity versus temperature for oil with different API is presented in Figure 2.
In the presence of water in of crude in the form of a water emulsion then the sound speed increases with an increasing of amount of water, Figure 3.
As follows from these graphs, the sound speed decreases almost linearly with decreasing % of water. It is interesting to compare the calculated data of sound speed with real measurements of sound speed in different types of crude. Direct measurements of sound speed are presented on Figure 4. For each of six tanksthe sound speed data has been measured in 6 - 8 entry points. Four tanks contained light oil and two tanks were filled with medium oil. Since the measurements were performed at different temperatures (16 - 21)˚C, the experimental data is recalculated to the same temperature of 20˚C using the formula (3) for oil with API0 40.
It is seen from this data that formula (3) is a quite satisfactory approximation for the evaluation of sound speed, but in practical conditions it is better to measure sound speed directly in the actual tank environment, because possible errors of evaluated inclined distances can be meaningful.
2.3. Sound Attenuation and Absorption in Crude
The general weakening of the acoustic energy ofin sound waves propagating in crude (α∑-attenuation) is determined not only by classical absorption but also by scattering of sound by various irregularities that are always present in crude oil. Such irregularities are dissolved gas bubbles, water droplets and solid particles of sand and other minerals. Therefore general attenuation is [2]
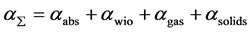 (4)
(4)
where
αabs—absorption coefficient, which depends on f2αg, αw, αp,—coefficients of sound attenuation due to scattering from gas bubbles, water droplets and solid particles, respectively.
It is difficult to quantify the level of scattering by the water droplets because it depends on many factors—the droplet’s size, pressure, temperature, frequency and type of crude oil. The presence of dissolved gas also leads to
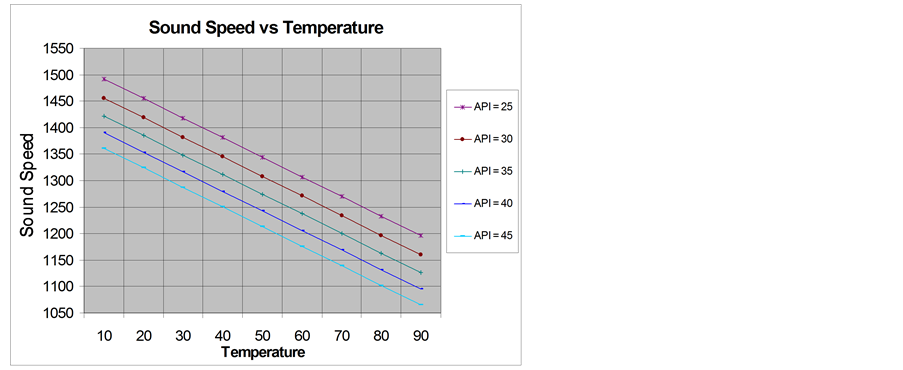
Figure 2. Sound speed in crude oil versus temperature for different API.

Figure 3. The speed of sound in the crude oil versus % of water content.

Figure 4. Experimental data of sound speed versus calculated value at T = 20˚C for API 40.
weakening of sound, and can be significant, if the operating frequency is the resonant frequency of the gas bubbles. The level of scattering due to bubbles also depends on their concentration, bubble size, temperature, pressure, frequency and type of oil. If it is assumed that in a crude tank, the relative concentration of the gas bubbles is not very big (τN < 10−5), where τN = τkN, then in accordance with [7] additional sound attenuation in oil containing N bubbles of radius rkin 1 cm3 radius, is equal to:
 (5)
(5)
where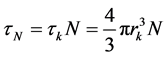 , and resonance frequency of gas bubble is determined from relation
, and resonance frequency of gas bubble is determined from relation 
For the frequency range 100 - 200 kHz the largest contribution comes from bubbles with a radius of 3.26 (2−10 - 3−10) mm. For example, if a 1 cm3 volume contains one resonant gas bubble at 150 kHz, the additional attenuation will be about 0.015 dB/m, which is quite significant. It should also be noted that small bubbles can “live” in the viscous oil for a very long time since their ascent rate is very low. For example, the ascent rate of a bubble with diameter 50 micron in water is less than 0.0005 m/sec, and in oil with a kinematic viscosity of 5 - 7 cSt this rate can be 100 - 1000 times less. The presence of solid particles suspended in the crude oil also leads to an additional attenuation due to the friction, scattering, and internal losses. We have no experimental data on the concentration of particles of various impurities in the crude oil and their size distribution. Therefore, for a rough estimation of the attenuation one can use the empirical formula for water and little concentrated suspensions [8]
 (6)
(6)
where 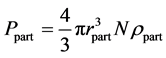 The dependence of the Ap on frequency and size of the particles is shown in Figure 5
The dependence of the Ap on frequency and size of the particles is shown in Figure 5
For example, for averaged particle with diameter of 30 microns, concentration of 0.025 to 0.7 kg/m3 and frequency 150 kHz the additional attenuation can be from (0.007 to 0.05) dB/m. Note that these irregularities are always present in the crude oil. Figure 6 shows the results of laboratory analysis of crude oil samples taken from 6 different storage tanks (different oil fields).
From these data it follows that the real attenuation of sound waves in crude will be always more than pure absorption and this feature should be considered in the design of acoustic tools for correct selection of their operating frequency and source level. Figure 7 confirms this thesis.
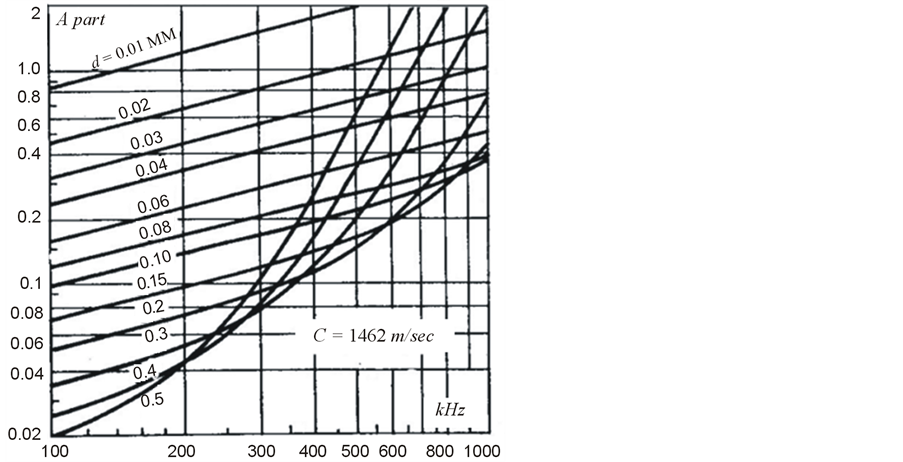
Figure 5. The frequency dependence of the coefficient Ap for particles of different size.
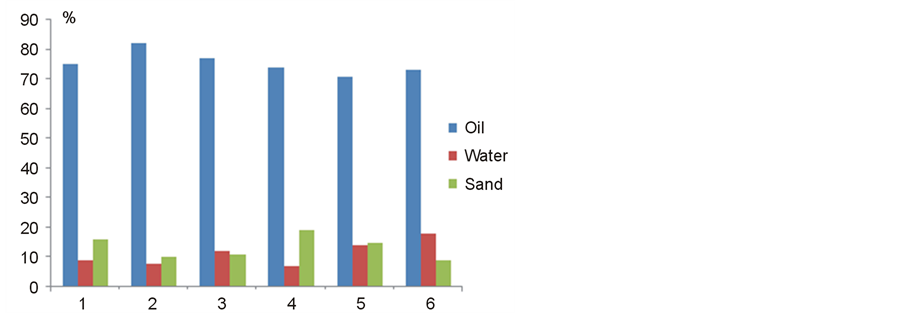
Figure 6. Content of crude in 6 different storage tanks.
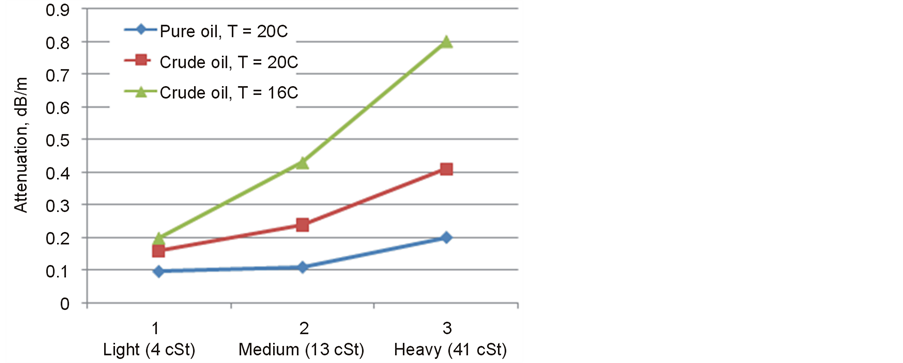
Figure 7. Attenuation on F = 150 kHz in pure oil and crude oil (experimental data).
2.4. Parameters of Sludge
Knowledge of sludge parameters is necessary for the correct selection of carrier frequency and evaluation of energy balance for the acoustic profiling tool, since the coefficient of backscattering from sludge is a very critical parameter depending on angle of illumination and differences in the acoustical impedances of oil and sludge. Oil sludge compositions are extremely varied and complex systems consisting of oil, water and mineral fraction (sand, clay, silt, etc., the ratio of which can vary over very a broad range. On average sludge can contain (by weight) oil (10 ... 60%), water (30 ... 85) % and solids (up to 45%). A more detailed analysis shows that the organic part of sludge, except for free oil hydrocarbons, contains asphaltenes, paraffin and nonorganic inclusions such as iron oxides, sulfides and so forth. Figure 8 presents the content of sludge from different storage tanks [6] .
Viscosity and density for these samples are presented on Figure 9.
We specially considered a large number of storage tanks to emphasize that the sludge composition always varies between tanks. It is seen that the density of sludge varies from 950 to 985 kg/m3 and its viscosity can reach 1750 MPa*sec. The solids content is up to 21%, water is up to 40%, Hydrocarbon part can contain 21% of paraffin, 19% of resins and 18% of asphaltenes. It should be noted that due to complex chemical reactions in oil tanks the sludge parameters may change over time, and if the oil tank wasis not in operation for a long time the sludge viscosity may increase so that its structure becomes almost solid and can include hard water scale deposits. This causes large differences in the acoustic impedances of crude and sludge, which of course, makes it easier for acoustic detection, but significantly hinders operations to remove such sludge. However, we shall note that in the crude oil tanks, the boundary between the crude oil and sludge is not sharp. Laboratory samples of sludge from tanks indicate that the sludge is composed of three layers: the first layer—is an actually crude itself but with some percentage of different suspensions. It is practically impossible to detect this layer on the frequencies which are used for acoustic sludge profiling. The second layer is the “transition layer”. It is also sludge, but its viscosity and density are less than the third sludge layer. The thickness of the transition layer can range from a few millimeters to ten centimeters or more. The acoustic impedances and backscatter coefficients of the transition layer are not known. But the very important issue is that the presence of the transition layer, if this layer is detected, can be the source of additional errors of in estimation of the sludge volume. The existence of the transition layer is illustrated in Figure 10, which shows the results of direct measurements of the density of the crude oil. It is evident that there is a transition layer with a thickness of more than 10 cm.
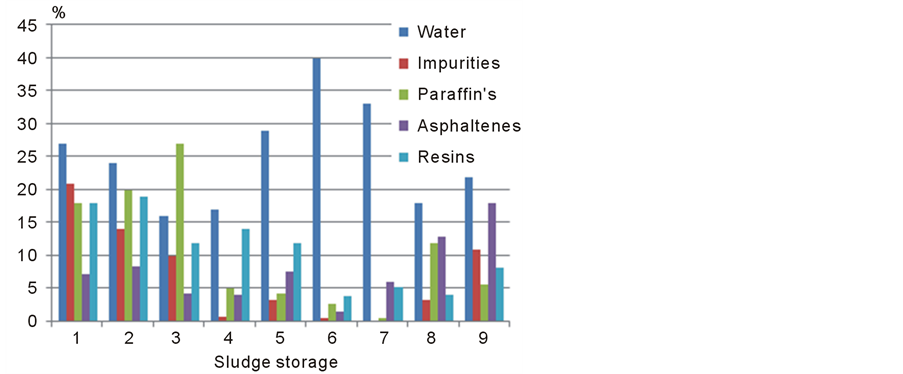
Figure 8. Content of sludge in 9 sludge storage tanks.
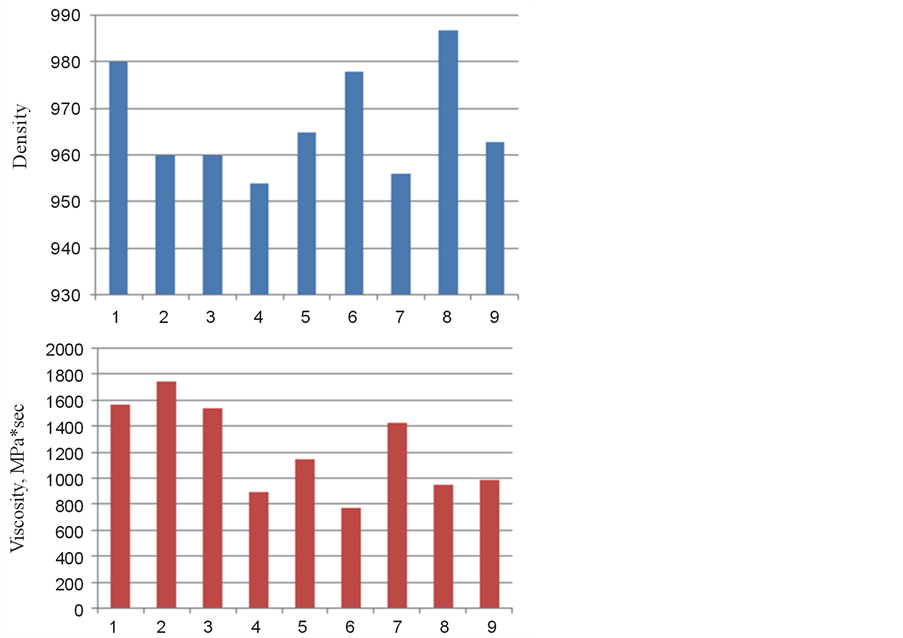
Figure 9. Density and viscosity of sludge in different sludge storages.
The problem in detecting the transition layer is closely related to the values of acoustic impedances for sludge and crude oil. We can directly measure the acoustic impedance of crude oil using measurements of sound speed and density. The problem is how to measure sound speed in the sludge? Unfortunately such data is not available in published literature. The simplest way is direct measurement. However, the realization of such measurements needs to have an echo-sounder with a low operating frequency, since the absorption in sludge is very high due to the very high viscosity. Then knowing the height of the tank, the level of oil, depth of immersion of tool, sound speed in oil and density of the sludge it is possible to measure sound speed in sludge using measured time of flight of forecho-signals reflected from the metal bottom and sludge surface. However, the need to have an additional lower-frequency measuring channel significantly complicates the equipment and increases its cost.
Therefore, we can proceed as follows. We can estimate the sound speed in sludge, using data on the density and viscosity of the sludge and comparing this with known experimental data for the refined petrochemical products of crude oil, which have similar viscosity and density to the analogous parameters of the sludge. Such products range between diesel oil and lubricating oils. Because the mentioned parameters are similar, it does not matter that chemically these substances are different. Experimental data for some petroleum products are presented in Table 1
Experimental data for sound speed versus viscosity for these products and an approximation curve are presented in Figure 11.
The approximation curve describes quite well the behavior of sound speed in high-viscosity oil products and it can be used for estimation of sound speed in sludge. Now, using the obtained data, we can estimate the acoustic impedances of oil and sludge, and calculate the coefficients of reflections from sludge, which in turn will allow the estimation of the levels of scattering echo signals and correct calculating the energy balance of the acoustic profiler.
2.5. Temperature Gradients
The temperature distribution inside the tank may not be uniform. Typically, vertical temperature gradients are the most significant, although in some conditions horizontal gradients can arise. The presence of vertical temperature gradients causes the refraction of sound waves, which in turn can lead to errors of measured slant ranges and, ultimately, errors of volume. Figure 12 shows measurements of the density and temperature of oil versus depth, for a small oil tank of about volume 3000 m3 and a height of 11 meters.
Calculated ray traces for this temperature profile are presented on Figure 13. It is clearly seen that the refraction of sound rays can be significant. Compare the position of two reflecting points (A and A¢) where the inclined distances differ on 25 meters! Therefore, when there is a significant vertical temperature profile, the resulting refraction of acoustic waves must be taken into account when calculating the surface and its shape corrected. It can be seen that for a given vertical temperature profile, refraction of rays can be substantial, and the position of the reflecting surface point can be evaluated properly and with great accuracy.

Table 1. Parameters of petrochemical products.

Figure 11. Experimental data on sound speed in petroleum products and approximation curve. (Data provided courtesy of G.M. Volk).

Figure 12. The vertical profile of temperature and density in 8 hours after filling the tank with heated oil.
3. Geometry of Measurements
Typically the height of large storage tanks does not exceed 15 - 18 meters, while their diameter may range from 35 to 120 meters and the oil level can be from 10 to 17 meters. Given that the number of possible entry points is limited, the problem of where to install the array arises. It is desirable to provide maximum coverage from one entry point; therefore the installation of the array parallel to the bottom of the tank is not appropriate since the illuminated area becomes very small. Therefore generally acoustic profilers use an inclined array at a certain vertical angle. However, the vertical inclination of the array creates two negative effects. Inclined illumination causes a weak level of backscattering signals from the sludge surface and the character of backscattering becomes close to isotropic, which in turn reduces the effectiveness of the correlation processing of complex broadband signals. The transmitter power and resulting source level is limited by the heat dissipation capability of the immersed array. The only way to increase the signal/noise ratio is to use complex signals with correlation processing. But the isotropic character of scattering leads to de-correlation of complex signals and gain of correlation processing becomes small compared with the radiation of a simple tone burst. There is no reliable data on backscattering levels of echo-signals from sludge. For rough estimations we will use published data for different bottom types in fresh water [7] , Figure 14.
Because the surface of sludge is more similar to irregular silt the design of the acoustic profiler should mostly focus on plots 1 and 2, therefore the averaged backscattering level can be estimated as about -(25 - 30) db.

Figure 13. Ray traces for uniform and vertical temperature profiles.

Figure 14. Levels of backscattering for different types of the bottom in fresh water versus sliding angle. 1. Fine sand. 2. Irregular silt 3. Large sand, gravel 4. Stones (10 × 10 × 10 cm in average).
4. Accuracy of Measurements
What could be the real measurement error of the sludge volume? Despite the fact that the technical (system) accuracy of the profiling tool can be very high, the actual error of a measured sludge volume may not reflect this. The operating frequencies used in these systems generally lies in the range from 120 kHz to 200 kHz and slant ranges, which determine the local heights of sludge, may be estimated with a very high accuracy using short pulses or complex signals. The range resolution for a simple pulse signal is equal to  or
or 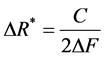
for complex signal and may be adjusted from 0.5 cm to 2.0 cm, where C—the sound speed in oil, τ—pulse length, ΔF—bandwidth. The mean-square error of measurements of slant range depends on output signal/noise ratio,
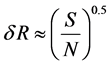 . Therefore the relative error
. Therefore the relative error 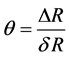 can be very small at high output signal/noise ratio, S/N.
can be very small at high output signal/noise ratio, S/N.
However, this small relative error does not guarantee the same error of measured volume. There are two types of errors—systematical and random. The nature of systematical errors is the errors of positioning of the tool, incorrect information on the co-ordinates of entry points and so on. We will not consider them. The main source of errors is errors in the measured sound speed and reverberation effects.
4.1. Refraction Errors
Let us review in short the principle of acoustic profiling to understand the influence of refraction errors, Figure 15.
Regardless of the type of array, it creates a narrow beam (or beams) which can scan in the vertical and horizontal planes. The width of beam determines the angle resolution and the covered partial area of the sludge surface. The principles of beamforming can be different—2D full sampled arrays, Mills cross, interferometry arrays and so on. Let us propose that the sludge surface has one reflecting point and the distribution of temperature in tank is uniform. Our goal is to estimate the height of this point. First of all we measure the slant distance to this point, knowing the time of flight τ of the echo signal.
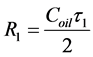 (7)
(7)
Because we know the vertical steering angle φ1 we can calculate ho as ho = R1Sin φ1 and the required height of sludge h1,
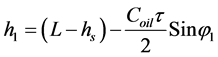 (8)
(8)
Acting similarly for all scanning horizontal and vertical angles we can define all theheights of a surface h(x,y). The result of such measurements is the cloud of points h(x,y) which describes the sludge surface in a discrete form, Figure 16. Interpolation procedures are then applied to get the final image of thesurface.
Note that thepartial volumes are presented as “cylinders”, though in reality they will have another form. The volume of sludge is the sum of all partial volumes but there is an unknown parameter—sound speed Coil..
Strictly speaking, system parameters such as phase shifts or time of delays which are used in beamforming procedures also depend on the speed of a sound. In particular, the volume of cylinder is equal to:
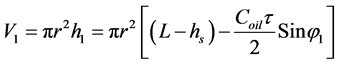 (9)
(9)
Total volume will be the sum of (9)
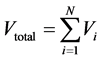 (10)
(10)
It follows from (8) that errors of volume ∆V are proportional to errors of sound speed ΔCoil,
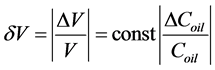 (11)
(11)

Figure 16. Discrete 3D sludge topography (no interpolation), values of heights are marked by conditional colors.
Note ΔC can be positive or negative. However, sound velocity also depends on the temperature (3). Therefore, when measuring the sound speed we must also measure the temperature.
Roughly the accuracy of sound speed in real conditions can be +/‒ 2% - 3% and the accuracy of measured sludge volume directly depends on this accuracy.
Now let us consider themore complex case when oil has a vertical temperature gradient like thedependence in Figure 7.
Because of thenon-uniform distribution of sound speed with depth thesound rays will refract. The presence of refraction can affect theaccuracy of themeasurements of heights and consequently, the error of volume, Figure 17.
Let us suppose that we formed a vertical beam with angle α0. In some time we receive a reflected signal from distance R = C0t. C0—is the speed of sound we have measured at point A.
Because of refraction the vertical beam generated with vertical angle α0 will be bent and result in the distance R = Ct, and (C ≠ C0!).We will get the reflection from point B and the image of this point is true. In other words, angle α is a true angle and angle α0 is the apparent angle. Therefore the height h0 is the apparent height. Its value is only true for a homogeneous environment. Since point B has a different height from point A, it means, that there is an error in the measurement of height h0.. An inhomogeneous environment will cause errors in the vertical angle that will result in errors in the estimation of heights.
The true height is equal to:
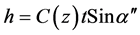 (12a)
(12a)
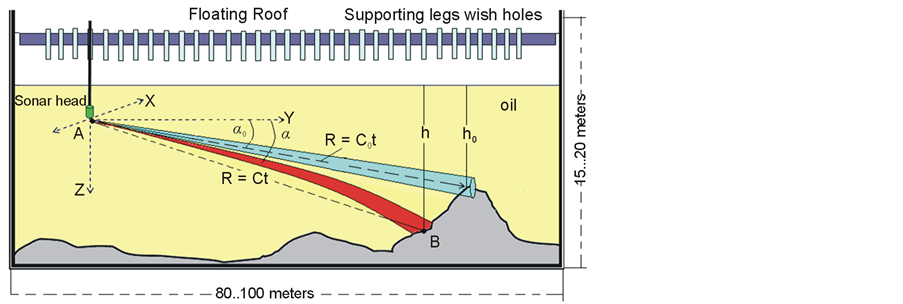
Figure 17. Errors of measured height in a vertical plane.
and the apparent height is equal to
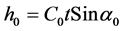 (12b)
(12b)
where C—some average sound speed on the line AO C0—sound speed in a point A t—double time of flight from array up to reflecting point.
The true height h can be calculated if we can calculate time of flight along the refracted ray knowing sound speed profile and angle α0 [7]
 (13)
(13)
In Equation (13) all parameters are known except the true height.
Because of complex function of n(z) for real environments integral (13) can be calculated by numerical methods. There is only one simple case where we can calculate (13) analytically.
If 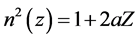 (14)
(14)
and 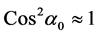 and
and 
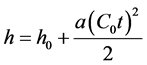 (15)
(15)
Therefore the correction factor is equal to
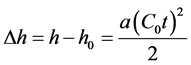 (16)
(16)
Note that the coefficient a can be positive or negative. Equation (16) is only true for small vertical angles. For arbitrary angles of vertical scanning
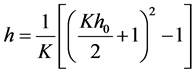 (17)
(17)
where
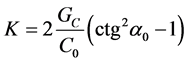 (18)
(18)
The results of calculations using (16) and the vertical profile in Figure 13 are presented in Figure 18. Note that this data is only to illustrate the influence of refraction on the accuracy of measurements.
Note that the height of the sludge surface is equal to
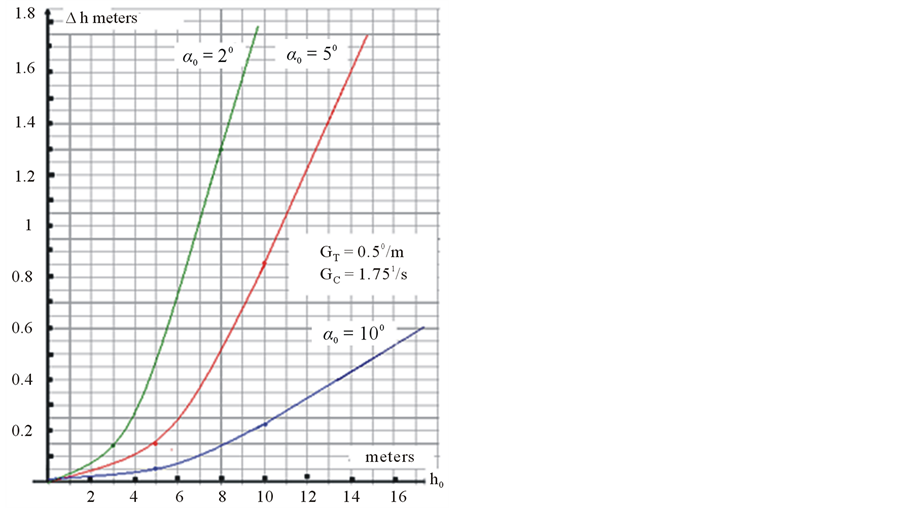
Figure 18. Errors on height versus seemed measured height at different angles of vertical scanning.
 .
.
From Figure 18 we can conclude that non-uniform distribution of temperature in the oil can lead to significant errors in measuring the form of a surface because of refraction. The error values depend on the vertical scanning angles sector and the values of gradients of temperature and sound speed.
4.2. Reverberation Errors
The second main source of errors is the reverberation of spurious signals received and generated by the main and side lobes of the transmitting and receiving arrays. These false signals appear as a result of the reflection of the pulses from metallic supports the roof, tank walls and various structures located on the bottom (heaters, pipes, etc.). Despite the fact that the arrays typically use apodization to decrease the side field, the levels of spurious side echo signals reflected from the metal structures can still exceed the useful weak echoes from sludge and, in addition, they can appear in unpredictable places. If such signals fall in the area of the sludge surface, they create additional “peaks” or “false” reflection points on the surface, which lead to an incorrect evaluation of heights and incorrect estimation of the volume. It usually leads to an over estimation of the sludge volume Figure 19 shows an example of a two-dimensional distribution of intensity echoes (in in a tank with a diameter of 60 meters).
The sludge surface looks like a cloud of non-uniform brightness; it is outlined by a closed curved red line. The strong echoes like “dashes” visible on the surface of the sludge and beyond it are generated by the reflections from the roof supports. Some of them are received by the main lobes of the array and some of them are generated by the side lobes. The presence of these signals leads to incorrect reproduction of the surface shape of the sludge; refer to the left image in Figure 20. It can be seen that the sludge surface has heights up to 6 m in some places, while the average height of sludge does not exceed 1.9 m. The presence of these spurious signals leads to an overestimation of sludge volume: 3262 m3 versus the real volume of 2764 m3.
This example implies that the development of acoustic sludge profiling systems should strive to minimize the level of side lobes in the arrays and use more sophisticated signal processing algorithms.
Accounting for these cumulative errors and the experience of making field measurements results in an error of the sludge volume in the range 3% to 5%. This value of the error is typically indicated by developers of similar equipment.
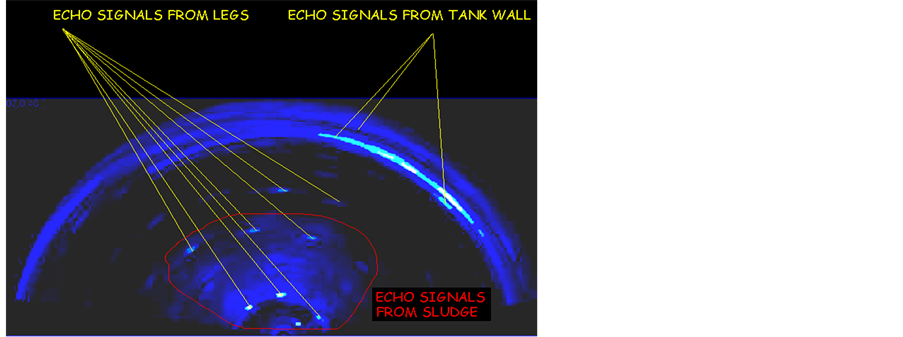
Figure 19. 2D distribution of intensities of echo-signals in tank.

Figure 20. Wrong and true image of sludge surface.
5. Conclusions
1). Considered features of sound propagation in the crude oil, located in large closed metal containers and their specific design can significantly affect both the structure of the arrays, and the signal processing algorithms, which may significantly differ from the usual methods of acoustic bathymetry in oceanography.
2). The description of the basic laws of propagation of acoustic signals in the crude oil and their dependence on various parameters can serve as a basis for the development of acoustic profiling systems, selection of the optimal frequency, size of the arrays and the required source level.
3). To minimize the possible errors in the calculated image of the sludge surface and its measured volume it is desirable to measure the vertical temperature profile and sound speed in all entry points.
4). In general, the signal processing algorithms should include procedures to compensate for refraction effects and suppression of false echo-signals caused by reverberation effects.
5). During inspection of crude oil tanks, the satisfaction of these conditions allow to obtain an error value of measured sludge volume in the range 3% to 5%.