Effects of Hall Current on MHD Boundary Layer Second-Order Viscoelastic Fluid Flow Induced by a Continuous Surface with Heat Transfer ()
1. Introduction
Most of the time Hall current was ignored in applying Ohm’s law because it has no extraordinary effect for small and average values of the magnetic field. The effects of Hall current are very important in the presence of a strong magnetic field [1] , because for strong magnetic field electromagnetic force is prominent. The recent research for the applications of MHD is towards a strong magnetic field, due to which study of Hall current is very important. Actually, in an ionized gas of low density subjected to a strong magnetic field, the conductivity perpendicular to the magnetic field is decreased by free spiral movement of electrons and ions about the magnetic lines of force before suffering collisions. A current produced in a direction at right angle to the electric and magnetic fields is called Hall current. The important engineering applications for MHD boundary layer flows with heat transfer including the effects of Hall current are encountered in MHD power generators and pumps, Hall accelerators, refrigeration coils, electric transformers, in flight MHD, solar physics involved in the sunspot development, the solar cycle, the structure of magnetic stars, electronic system cooling, cool combustors, fibre and granular insulation, oil extraction, thermal energy storage and flow through filtering devices and porous material regenerative heat exchangers. Some interesting studies regarding the effects of Hall current on MHD boundary layer flow are as follows:
Zaman [2] recently examined the effects of Hall current on the unsteady incompressible MHD fluid flow with slip conditions and porous walls. Ayub et al. [3] considered the effects of Hall current on hydromagnetic flow and heat transfer in a second grade fluid over a stretching sheet. The effects of Hall current on unsteady MHD flows of a second grade fluid are studied by Ahmad et al. [4] . Hall effects on hydromagnetic flow over a surface stretching with a power-law velocity and unsteady duct flow of a non-Newtonian fluid in a porous medium are investigated by Hayat et al. [5] [6] . The effects of Hall current and heat transfer on flow due to a pull of eccentric rotating disks are discussed by Asghar et al. [7] . Khan et al. [8] described the Hall effects on the pipe flow of a Burgers’ fluid. Abo-Eldahab et al. [9] [10] analyzed the effects of Hall current on the mixed convection and free convection boundary layer flows of non-Newtonian and micropolar fluids. Debnath et al. [11] investigated the effects of Hall current on unsteady hydromagnetic flow past a porous plate in a rotating fluid system. The study of boundary layer flows from a continuous surface is important because it is involved in a large number of engineering processes. Since in the remarkable work of Sakiadis [12] such flows are studied extensively through various aspects, the literature on the topic is quite rich.
The present paper is devoted to study the effects of Hall current on heat transfer and MHD boundary layer flow induced by a continuous surface in a parallel free stream of a second-order viscoelastic fluid. The resulting Hall current problem is solved by means of homotopy analysis method (HAM) [13] -[19] , which is very powerful and efficient in finding the analytic solutions for a wide class of nonlinear differential equations. The method gives more realistic analytic solution that converge very rapidly in physical problems. The convergence region for the complex nonsimilar series solution is found with the help of  -curves. The effects of Hall current on the real and imaginary parts of velocity and temperature are seen for suction/injection with the help of graphs. Tables are constructed to discuss the effects of Hall current on magnitude of shear stress at the surface and rate of heat transfer at the surface for suction/injection.
-curves. The effects of Hall current on the real and imaginary parts of velocity and temperature are seen for suction/injection with the help of graphs. Tables are constructed to discuss the effects of Hall current on magnitude of shear stress at the surface and rate of heat transfer at the surface for suction/injection.
2. The Problem and Its Solution with Convergence Check
The arising nonlinear problems for flow and heat transfer with effects of Hall current are [20] [21]
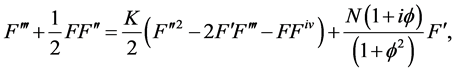 (1)
(1)
 (2)
(2)
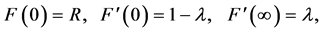 (3)
(3)
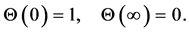 (4)
(4)
where prime indicates the differentiation with respect to 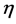 only, where
only, where 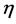 is the distance from the surface,
is the distance from the surface, 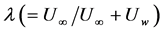 is the velocity ratio,
is the velocity ratio,  is the suction/injection parameter,
is the suction/injection parameter,  is the suction/ injection velocity,
is the suction/ injection velocity, 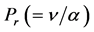 is the Prandtl number,
is the Prandtl number, 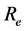 is the Reynold number,
is the Reynold number,  is the second grade fluid parameter,
is the second grade fluid parameter,  is the Eckert number,
is the Eckert number,  is the dimensionless temperature,
is the dimensionless temperature, 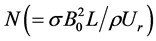 is magnetic parameter and
is magnetic parameter and 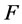 is the dimensionless stream function,
is the dimensionless stream function, 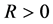 corresponds to suction and
corresponds to suction and 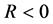 corresponds to injection. It is noticed that the nondimensional problems defined by above equations are nonsimilar. For analytic HAM solutions the initial approximations of
corresponds to injection. It is noticed that the nondimensional problems defined by above equations are nonsimilar. For analytic HAM solutions the initial approximations of  and
and 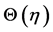 are
are
 (5)
(5)
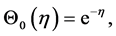 (6)
(6)
and the auxiliary linear operators are
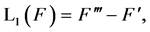 (7)
(7)
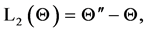 (8)
(8)
Following the HAM and trying higher iterations with the unique and proper assignment of the results converge to the exact solution:
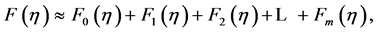 (9)
(9)
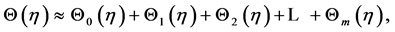 (10)
(10)
using the symbolic computation software such as MATLAB, MAPLE or MATHEMATICA successively obtain
 (11)
(11)
 (12)
(12)
The complete complex nonsimilar analytic solutions are
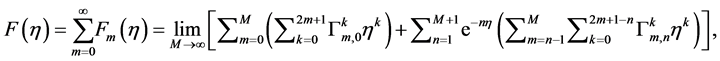 (13)
(13)
 (14)
(14)
The coefficients 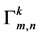 and
and  can be computed by using
can be computed by using
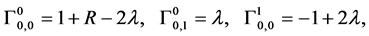 (15)
(15)
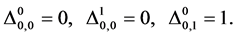 (16)
(16)
given by the initial guess approximations in Equations (5) and (6).
We know that convergence region and rate of approximation for the homotopy analysis method (HAM) depend upon homotopy parameters  and
and . Therefore the
. Therefore the  -curves are sketched for
-curves are sketched for 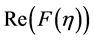 and
and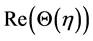 . Figure 1 and Figure 2 show that the range for the admissible values of
. Figure 1 and Figure 2 show that the range for the admissible values of 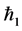 and
and 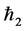 are
are 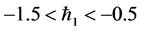 and
and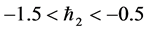 , respectively. The computations made show that the series of the dimensionless stream function in Equation (13) converges in the whole region of
, respectively. The computations made show that the series of the dimensionless stream function in Equation (13) converges in the whole region of 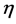 when
when 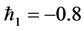 and series (14) converges in the whole region of
and series (14) converges in the whole region of 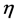 when
when 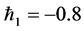 and
and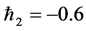 .
.
3. Graphs, Tables and Discussion
In order to discuss the effects of Hall current  on the flow field the graphs are drawn for the variation of the real and imaginary parts of the velocity profile
on the flow field the graphs are drawn for the variation of the real and imaginary parts of the velocity profile 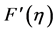 with distance from the surface
with distance from the surface  and for the real and imaginary parts of the shear stress at the wall for different values of the suction/injection parameter
and for the real and imaginary parts of the shear stress at the wall for different values of the suction/injection parameter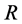 , velocity ratio
, velocity ratio , second grade fluid parameter
, second grade fluid parameter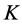 , magnetic field parameter
, magnetic field parameter  and the homotopy parameter
and the homotopy parameter 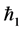 at constant wall temperature.
at constant wall temperature.
Figure 3 and Figure 4 elucidate the variation of the real and imaginary parts of the velocity profile 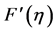 with
with  for suction respectively. Figure 3 shows that for fixed values of
for suction respectively. Figure 3 shows that for fixed values of ,
, 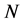 ,
,  ,
,  and
and 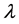 with increase in Hall current
with increase in Hall current 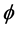 real part of the velocity increases for suction. Figure 4 describes that for fixed values of
real part of the velocity increases for suction. Figure 4 describes that for fixed values of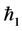 ,
, 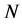 ,
, 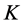 ,
, 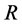 and
and 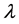 with increase in Hall current
with increase in Hall current 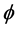 imaginary part of the velocity increases in magnitude for suction. Similar behavior is observed for injection. In Figure 3 and Figure 4 boundary layer structure is observed and the boundary layer thickness increases with increasing Hall current
imaginary part of the velocity increases in magnitude for suction. Similar behavior is observed for injection. In Figure 3 and Figure 4 boundary layer structure is observed and the boundary layer thickness increases with increasing Hall current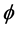 , which results in thick-
, which results in thick-
ening of the boundary layer. Hence, as expected, the velocity increases with increasing Hall current . This is due to the fact that the effective conductivity decreases with increasing Hall current
. This is due to the fact that the effective conductivity decreases with increasing Hall current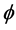 , which reduces the magnetic damping force on the velocity. Figure 5 shows the variation of the real part of the skin friction coefficient
, which reduces the magnetic damping force on the velocity. Figure 5 shows the variation of the real part of the skin friction coefficient  with
with 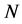 for several values of Hall current
for several values of Hall current 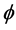 for suction. It is found that with increasing Hall current
for suction. It is found that with increasing Hall current 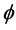 the skin friction coefficient decreases at all points for suction. Figure 6 indicates the variation of the real part of the skin friction coefficient
the skin friction coefficient decreases at all points for suction. Figure 6 indicates the variation of the real part of the skin friction coefficient 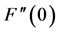 with suction / injection parameter
with suction / injection parameter  for several values of Hall current
for several values of Hall current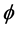 . From Figure 6 it is seen that with increase in Hall current
. From Figure 6 it is seen that with increase in Hall current 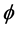 real part of the skin friction coefficient
real part of the skin friction coefficient 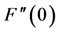 decreases. When magnetic field is applied perpendicular to the fluid velocity then it gives rise to a drag-like or resistive force which slow down or suppress the motion of the fluid on the surface. This leads to a reduction in the velocity of the fluid and flow rates. With the increase in the strength of the magnetic field the motion of the particulate suspension on the surface reduces due to which skin friction coefficient reduces as in Figure 5 and Figure 6.
decreases. When magnetic field is applied perpendicular to the fluid velocity then it gives rise to a drag-like or resistive force which slow down or suppress the motion of the fluid on the surface. This leads to a reduction in the velocity of the fluid and flow rates. With the increase in the strength of the magnetic field the motion of the particulate suspension on the surface reduces due to which skin friction coefficient reduces as in Figure 5 and Figure 6.
In order to discuss the effects of Hall current 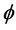 on the temperature field
on the temperature field 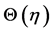 the graphs are plotted for different order of approximations for the variation of the real and imaginary parts of
the graphs are plotted for different order of approximations for the variation of the real and imaginary parts of 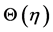 with distance from the surface
with distance from the surface 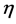 and for the real and imaginary parts of the local Nusselt number
and for the real and imaginary parts of the local Nusselt number 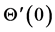 for different values of the seven dimensionless parameters (i) suction/injection parameter
for different values of the seven dimensionless parameters (i) suction/injection parameter 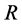 (ii) velocity ratio
(ii) velocity ratio  (iii) elastic parameter
(iii) elastic parameter 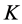 (iv) magnetic field parameter
(iv) magnetic field parameter 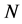 (v) homotopy parameters
(v) homotopy parameters ,
, 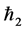 (vi) Prandtl number
(vi) Prandtl number  and (vii) Eckert number
and (vii) Eckert number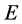 .
.
Figure 7 and Figure 8 depict the variation of the real and imaginary parts of the temperature profile  with
with 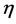 for several values of the Hall current
for several values of the Hall current 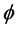 for suction. It is observed from Figure 7 that for fixed values of
for suction. It is observed from Figure 7 that for fixed values of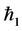 ,
, 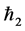 ,
, 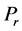 ,
, 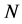 ,
, 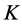 ,
, 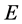 ,
, 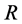 and
and  with increase in Hall current
with increase in Hall current 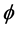 real part of the temperature distribution increases for suction. Figure 8 shows that imaginary part of the temperature
real part of the temperature distribution increases for suction. Figure 8 shows that imaginary part of the temperature 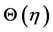 increases by increasing
increases by increasing . Same type of behavior is observed for injection. Figure 9 explains that for fixed values of
. Same type of behavior is observed for injection. Figure 9 explains that for fixed values of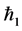 ,
,  ,
,  ,
, 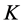 ,
, 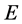 ,
, 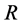 and
and 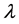 with increase in Hall current
with increase in Hall current 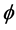 real part of the temperature gradient
real part of the temperature gradient 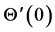 decreases at all points for suction and decreases for injection for all values of the Prandtl number
decreases at all points for suction and decreases for injection for all values of the Prandtl number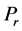 . Figure 10 elucidates that imaginary part of the temperature gradient
. Figure 10 elucidates that imaginary part of the temperature gradient 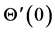 also decreases with increasing Hall current
also decreases with increasing Hall current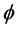 .
.
Table 1 shows the absolute values of skin friction coefficient 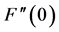 for Hall parameter,
for Hall parameter,
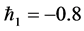
 . It is observed from Table 1 that a decrease in
. It is observed from Table 1 that a decrease in  leads to a reduction in the values of
leads to a reduction in the values of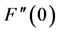 . It is also observed from Table 1 that for a fixed value of
. It is also observed from Table 1 that for a fixed value of 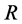 with increase in Hall current
with increase in Hall current 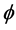 magnitude of shear stress at wall decreases. Table 2 indicates the absolute values of heat transfer rate
magnitude of shear stress at wall decreases. Table 2 indicates the absolute values of heat transfer rate 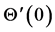 for
for
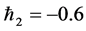

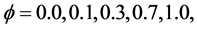
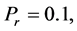 . We observed from Table 2 that for a fixed value of Hall current
. We observed from Table 2 that for a fixed value of Hall current 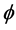 a decrease in the values of
a decrease in the values of 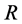 yields reduction in
yields reduction in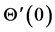 . Also for a fixed value of
. Also for a fixed value of 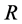 increase in Hall current
increase in Hall current 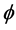 leads to a reduction in local Nusselt number
leads to a reduction in local Nusselt number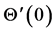 . It can be seen from Table 3 that for fixed values of
. It can be seen from Table 3 that for fixed values of 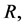
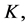

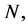
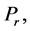

 and
and 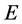 the magnitude of
the magnitude of 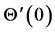 for suction decreases with an increase in Hall current
for suction decreases with an increase in Hall current 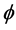 and for injection increases with an increase in
and for injection increases with an increase in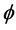 . Also for fixed values of
. Also for fixed values of 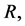
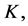
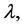

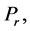
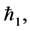
 and
and 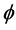 the magnitude of
the magnitude of 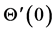 (for suction/injection) decreases by increasing Eckert number
(for suction/injection) decreases by increasing Eckert number .
.
4. Conclusions
In this study the Complex nonsimilar HAM solutions for the stream function and temperature are constructed on taking viscous dissipation and Hall currents into account. More significantly, the complex nonsimilar series solution clearly demonstrates how various physical parameters play their part in determining properties of the flow. The results are discussed under the effects of parameter 
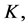
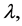
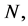

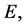
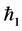 and
and  through graphs and tables. We have following observations:
through graphs and tables. We have following observations:
The Complex solution series for dimensionless stream function 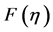 and dimensionless temperature function
and dimensionless temperature function 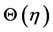 converges in the whole region of
converges in the whole region of 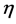 for
for 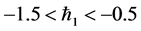 and
and .
.
Real and imaginary parts of the fluid velocity increases with increase in Hall current 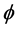 for suction/injection.
for suction/injection.
Real and imaginary parts of the fluid temperature increases with increase in Hall current 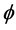 for suction/injection.
for suction/injection.
Boundary layer thickness increases for suction/injection with increasing Hall current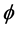 , which results in thickening of the boundary layer.
, which results in thickening of the boundary layer.
Absolute values of the skin friction coefficient decreases with increase in Hall current 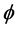 for suction/injection.
for suction/injection.
Increase in Hall current 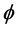 leads to a reduction in the absolute values of the local Nusselt number.
leads to a reduction in the absolute values of the local Nusselt number.