1. Introduction
Since the work of Black-Scholes in 1973 see [1] , the financial markets have expanded considerably and traded products are increasingly numerous and sophisticated. Most widespread of these products are the options. The basic options are the options to sell and purchase, respectively called put and call. If option can be exercised at any time until maturity, we speak about American option otherwise it is a European option.
The two researchers provide a method of evaluation of European options by solving a partial derivative equation called (black-Scholes’s equation). However, we cannot get explicit formula for pricing of American options, even the most simple. The formalization of the problem of pricing American options as variational inequality, and its discretization by numerical methods, appeared only rather tardily in the article of Jaillet, Lamberton and Lapeyre see [2] . A little later, the book of Wilmott, Dewynne and Howison see [3] has made it much more accessible the pricing by L.C.P from American Option problem. For the problems at free boundary several numerical results have been obtained for parabolic and elliptic variational and quasi-variational inequality see [4] -[8] .
For our part, we are interested to asymptotic behavior of V.I related to the American options problem. Where we adapted to our problem result obtained in [4] and we eliminated an additional factor
. We discretize the space 
by a space 
constructed from polynomials of degree 1 and the time by θ- scheme. Subsequently, we demonstrated the error estimate between the continuous solution and the discrete solution of the problem given by:
For
, we have
and for
, we have
We used the uniform norm, because it is a realistic norm, which gives us the approximation described above and which enables us to locate the free boundary, a crucial thing in practice of the American options.
The paper is organized as follows. In Section 2, we give the problem of American options as a parabolic variational inequality. In Section 3, we discretize by the finite elements method and we deal the stability of θ-scheme for our V.I. In Section 4, we adapt to our problem results obtained for similar problems see ([7] [9] ) namely a contraction associated with our problem which allows us to define an algorithm of Bensoussan-Lions [10] . Finally, in Section 5, we establish the estimate of the asymptotic behavior of θ-scheme by the uniform norm for American options problem.
2. Formulation of American Options Problem as Variational Inequality
In this section, we recall the context of our problem (see [11] -[13] ). An American option is a contract which gives the right to receive the payoff 
at some time
, where
. This payoff is then given as a function of the prices 
at the time t of n financial products constituting the underlying asset. Such as these prices are strictly positive, we set
(1)
and we express the payoff under the form
(2)
where
(3)
is a given regular function.
We assume that the following stochastic differential equation is satisfied by the logarithmic transformation of the prices
(4)
where 
is the interest rate, 
is invertible Volatility matrix and 
is a standard ndimensional Brownian motion defined on a probability space 
The Continuous Problem
Under some assumptions on financial markets (no-arbitrage principle) see [2] [14] and the above assumptions one can prove, that 
is a solution of the following parabolic inequality:
(5)
Now we will give the variational inequality related to American options problem in a more compact form, where we starts by giving new notations and imposed certain conditions.
By a change of variable
, the problem (5) becomes:
Find 
solution of
(6)
where K is a closed convex set defined as follows:
(7)
with
(8)
and 
is a bounded smooth domain in
, with boundary
.
A is an operator defined over 
by:
(9)
and the coefficients: 
where 
and 
are satisfy the following conditions:
(10)
(11)
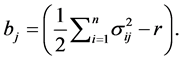(12)
f is a positive function.
For more detail on the parabolic inequality associated with American options problem (see [2] [13] [15] -[17] ).
We can reformulate the problem (6) to the following parabolic variational inequality:
(13)
where 
is a continuous bilinear form associated with operator A defined in (9). Namely,
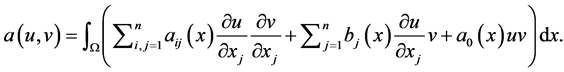(14)
Theorem 1 (Cf. [10] ): If
, the problem (13) has an unique solution 
Moreover, one has
(15)
3. Study of the Discrete Problem
We decomposed 
into triangles and let 
denotes the set of all those elements, where 
is the mesh size. We assume that the family 
is regular and quasi uniform. Let 
denote the standard piecewise linear finite element space, and 
be the matrix with generic coefficients 
where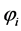
, 
, are the basis function of the space
, defined by 
where 
is a vertex of the considered triangulation.
We introduce the following discrete spaces 
of finite element constructed from polynomials of degree 1:
(16)
and
(17)
We consider rh be the usual interpolation operator defined by: 
(18)
The discrete maximum principle assumption (d.m.p): We assume that the matrix 
defined above is an M-matrix (Cf. [18] ).
Theorem 2 (Cf. [19] ): Let us assume that the bilinear form 
is weakly coercive in 
there exists two constants 
and 
such that
(19)
Notation:
3.1. Discretization
We discretize the space 
by a space discretization of finite dimensional 
constructed from polynomials of degree 1 and for the regularity of the solution see [20] . In a second step, we discretize the problem with respect to time using the θ-scheme. Therefore, we search a sequence of elements 
which approaches
, with initial data 
We apply the finite element method to approximate inequality (13), and the semi-discrete P.V.I takes the form of
(20)
Now, we apply the θ-scheme on the semi-discrete problem (20); for any 
and
, we have for 
(21)
where
(22)
(23)
We have 
that is admissible because
Thus we can rewrite (21) as: for 
and 
(24)
Thus, our problem (24) is equivalent to the following coercive discrete elliptic variational inequality:
(25)
Such that
(26)
3.2. Stability Analysis of θ-Scheme for the P.V.I
The study of the stability of θ-scheme for the American options problem is adapted to [4] .
It is possible to analyze stabilitytaking advantage of the structure of eigenvalues of the bilinear form 
and wecall that W is compactly embedded in 
since 
is bounded.
Let 
the eigenvectors of 
form a complete orthonormal basis of 
in the finite dimensional problem. At each time step
, can be expressed 
as well:
Moreover, let 
be the 
-orthogonal projection of 
into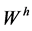
, that is, 
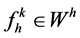, one has
We are now in a position to prove the stability for
, choosing in (21)
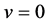, thus we have for 
(27)
For each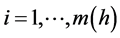
, the inequalities (27) is equivalent to
(28)
Since 
are the eigenfunctions means
(29)
If one solves relative to
, we find:
(30)
This inequality system stable if and only if
(31)
that is to say
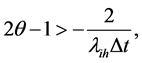(32)
means
(33)
So that this relation satisfied for all the eigenvalues 
of the bilinear form
, we have to choose their highest value, we take it for 
Lemma 1 (Cf. [4] ):
For 
the θ-scheme way is stable unconditionally i.e., stable 
And if 
the θ-scheme is stable unless
(34)
With
(35)
(spectral radius of
).
Notice that this condition is always satisfied if
. Hence, taking the absolute value of (30), we have
(36)
also we deduce that
(37)
Remark 1 (Cf. [4] ):
We assume that the coerciveness assumption (19) is satisfied with
, and for each
, we find
(38)
where
4. Existence and Uniqueness for Discrete P.V.I
We consider that 
and 
are respectively the stationary solutions of the following continue and discrete inequalities:
(39)
(40)
where the bilinear form 
satisfies the coercivity condition.
Theorem 3 (Cf. [9] ): Under the previous assumptions, and the maximum principle, there exists a constant C independent of h such that
4.1. A Fixed Point Mapping Associated with Discrete Problem
We consider the mapping
(41)
where 
is the unique solution of the following discrete coercive V.I: find 
Lemma 2 (Cf. [6] ): Under the d.m.p we have if 
then 
Proposition 1: Under the previous hypotheses and notations, if we set
, the mapping 
is a contraction in
, i.e.,
(42)
Therefore, Th admits a unique fixed point, which coincides with the solution of discrete coercive V.I (25).
Proof: For 
and
, we consider 
(respectively, 
solution to discrete coercive variational inequality (25) with right-hand side 
(respectively
).
Now, set
Since,
(because
).
So using Lemma 2 gives
On the other hand, one has
Indeed, 
is solution of
thus
Therefore
Similarly, interchanging the roles of 
and 
we also get
Consequently,
which is the desired result.
Remark 2: If we set
, the mapping 
is a contraction in
, i.e.,
(43)
Therefore, 
admits a unique fixed point, which coincides with the solution of discrete coercive V.I (25).
Proof: Under condition of stability, we have shown the θ-scheme is stable if and only if 
thus it can be easily show that
also it can be found that
which is the desired result.
4.2. Iterative Discrete Algorithm
We choose 
as the solution of the following discrete equation
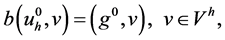(44)
where 
is a regular function given.
Now we give our following discrete algorithm
(45)
where 
is the solution of the problem (25).
Remark 3 cf. [7] : If we choose 
in (45) we get Bensoussan’s algorithm.
Proposition 2: Under the previous hypotheses and notations, we have the following estimate of convergence
(46)
And if 
(47)
Proof: We set a first case
, and we have
We assume that
so
thus
For a second case 
one can easily show that
which is the desired result.
5. Asymptotic Behavior
This section is devoted to the proof of principal result of the present paper, where we prove the theorem of the asymptotic behavior in 
-norm for parabolic variational inequalities.
Now, we evaluate the variation in 
between
, the discrete solution calculated at the moment 
and
, the continuous solution of (39).
Theorem 4: (The principal result). Under conditions of Theorem (3) and Proposition (2), we have for the first case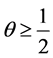 
(48)
and for the second case 
(49)
where C is a constant independent of h and k.
Proof: We have
thus
Then
Using the Theorem (3) and the Proposition (2), we have for 
and for 
we have
6. Perspective
In the following, we will consolidate our theoretical results by numerical simulation, which allows us to locate the free boundary, a very interesting thing in practice to calculate the price of the American options.
Acknowledgements
The authors would like to thank the editor and referees for her/his careful reading and relevant remarks which permit them to improve the paper.