Generalization of Uniqueness Theorems for Entire and Meromorphic Functions ()
1. Introduction
In this paper, the term “meromorphic” will always mean meromorphic in the complex plane C. Let a be a complex number and 
be a meromorphic function such that
. We say f and g share the value 
CM, if 
and 
assume the same zeros with the same multiplicities; if 
and 
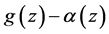assume the same zeros with the same multiplicities, then we say 
and 
share 
CM, especially we say that 
and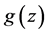 
have the same fixed-points when
. It is assumed that the reader is familiar with the notations of the Nevanlinna theory that can be found, for instance, in [1] . We denote by 
any function satisfying
as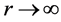
, possibly outside of finite measure.
Set
It is well known that if f and g share four distinct values CM, then f is a fractional transformation of g. In 1997, corresponding to one famous question of Hayman, C. C. Yang and X. H. Hua showed the similar conclusions hold for certain types of differential polynomials when they share only one value. They proved the following result.
Theorem A ([2] ). Let f and g be two non-constant meromorphic functions,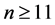 
be an integer and
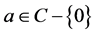. If 
and 
share the value a CM, then either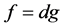 
for some 
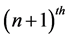root of unity d or 
and
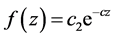, where 
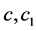and 
are constants and satisfy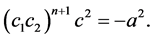 
In 2001, M. L. Fang and W. Hong obtained the following result.
Theorem B ([3] ). Let f and g be two transcendental entire functions,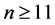 
an integer. If 
and 
share the value 1 CM, then
.
Recently, W. C. Lin and H. X. Yi extended the above theorem with respect to fixed point. They proved the following results.
Theorem C ([4] ). Let 
and 
be two transcendental meromorphic functions, 
an integer. If 
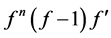and 
share z CM, then either 
or
where h is a nonconstant meromorphic function.
Theorem D ([4] ). Let 
and 
be two transcendental meromorphic functions, 
an integer. If 
and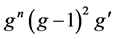 
share z CM, then
.
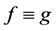We generalise the above results and prove the following Theorem.
Theorem 1.1 Let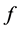 
and 
be two transcendental meromorphic functions, 
an integer. If 
and 
share 
CM then 
For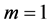
, we get Theorem C.
For
, we get Theorem D.
One may ask the following question, can the nature of the fixed point z be relaxed to IM in the above theorems?
In 2008, Meng Chao answered to the above question and proved the following theorems.
Theorem E ([5] ). Let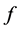 
and 
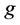be two transcendental meromorphic functions, 
an integer. If 
and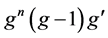 
share z IM, then either 
or
where h is a nonconstant meromorphic function.
Theorem F([5] ). Let 
and 
be two transcendental meromorphic functions, 
an integer. If 
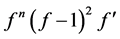and 
share z IM, then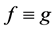
.
We generalise the above results and prove the following Theorem.
Theorem 1.2 Let 
and 
be two transcendental meromorphic functions, 
an integer. If 
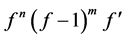and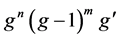 
share 
IM then 
For
, we get 
which improves Theorem E.
For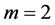
, we get
, we get Theorem F.
In 2002, Fang and Fang [6] proved that there exists a differential polynomial d such that for any pair of nonconstant entire functions f and g we can get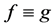
, if 
and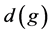 
share one value CM.
Theorem G ([6] ). Let 
and 
be two nonconstant entire functions, 
be a positive integer. If 
and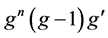 
share 1 CM, then
.
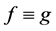In 2004, Lin-Yi [7] and Qiu-Fang [8] proved that Theorem G remains valid for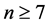
.
Theorem H ([7] [8] ). Let 
and 
be two nonconstant entire functions, 
be a positive integer. If 
and 
share 1 CM, then
.
We generalise the above results and prove the following theorem.
Theorem 1.3 Let f and g be two transcendental entire functions, 
an integer. If 
and 
share z CM then 
For
, 
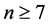we get Theorem H.
For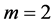
, 
, we get new result.
Fang-Fang discussed Theorem H by replacing CM with IM and proved the following Theorem.
Theorem I ([6] ). Let f and g be two nonconstant entire functions, n be a positive integer. If 
and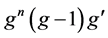 
share 1 IM and
, then
.
We generalise the above results and prove the following Theorem.
Theorem 1.4 Let f and g be two transcendental entire functions, 
an integer. If 
and 
share z IM then 
For
, 
which improves Theorem I.
For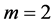
, 
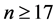, we get new result.
2. Some Lemmas
Lemma 2.1 ([9] ) Let f be a nonconstant meromorphic function, n be a positive integer. 
where ai is a meromorphic function satisfying 
. Then
Lemma 2.2 ([10] ) Let f be a non-constant meromorphic function k be a positive integer, then
where 
denotes the counting function of the zero’s of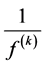 
where a zero of multiplicity m is counted m times if 
and p times if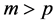
. Clearly
.
Lemma 2.3 ([11] [12] ) Let F and G be two nonconstant meromorphic functions sharing the value 1 IM. Let
If
, then
Lemma 2.4 ([5] ) Let f and g be two nonconstant meromorphic functions, 
, 
positive integers,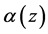 
denotes as in section 1 and
, and let
if F and G share 
IM, then 
Lemma 2.5 ([13] ) Let H be defined as above. If 
and
where 
and I is a set with infinite linear measure, then 
or
.
Lemma 2.6 ([14] ) Let 
then
where 
, which are distinct respectively.
3. Proofs of the Theorems
In this section, we present the proofs of the main results.
Proof of Theorem 1.2.
Lemma 2.4 implies that
.
Let
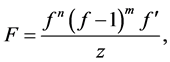(1)
(2)
and
(3)
(4)
where 
Thus we obtain that F and G share the value 1 IM. Moreover, by Lemma 2.1, we have
(5)
(6)
Noting that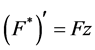
, we deduce
(7)
and by the First Fundamental Theorem,
(8)
Note that,
(9)
where 
are distinct roots of the algebraic equation
and
(10)
Since F and G share 1 IM, by Lemma 2.3, we have
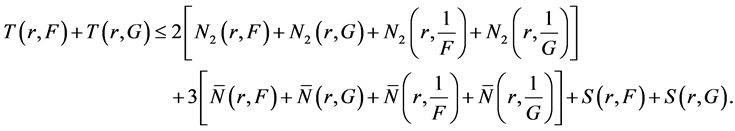(11)
Obviously, we have
(12)
(13)
So, we have
(14)
From (5) to (14), we have
(15)
We obtain that 
which contradicts
.
Therefore
, that is
(16)
By integration, we have
(17)
where 
and B are constants. Thus
(18)
Since,
(19)
we note that,
(20)
and
(21)
Similarly, we have
(22)
From (19) to (22) and applying Lemma 2.5, we get
or
.
We discuss the following cases.
Case (i) Suppose that
.
As in the proof of Theorem 1, in [5] we arrive at a contradiction.
Case (ii)
, thus
, that is,
Set
, we substitute 
in the above, it follows that
(23)
If h is not a constant, using Lemma 2.6 and (23), we conclude that
By (23), we get
where
Using Lemma 2.6, we get
where 
which are pairwise distinct.
This implies that every zero of 
has a multiplicity of at least n. By the Second Fundamental Theorem, we obtain that
, which is again a contradiction.
Therefore h is a constant. We have from (23) that
, which imply
, and hence
.
Proof of Theorem 1.1. Let F and G be given by (1) and (2). Suppose H is given as in Lemma 2.3, and
. Proceeding as in the proof of Theorem 1.2 we can obtain (3) to (10). Since F and G share 1 CM, by Lemma 2.3, we have
Hence from (3) to (10) and (12) to (14), we get
Hence
, which contradicts that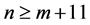
.
Proof of Theorem 1.4. Let F and G be given by (1) and (2). Suppose H is given as in Lemma 2.3, and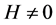
. Proceeding as in the proof of Theorem 1.2 we can obtain (3) to (10) and (11). Since F and G share 1 IM, by Lemma 2.3, obviously we have,
therefore (14) reduces to
Hence
, which contradicts that
. Proceeding in the same way as in Theorem 1.2 we get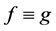
.
Proof of Theorem 1.3. Let F and G be given by (1) and (2). Suppose H is given as in Lemma 2.3, and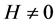
. Proceeding as in the proof of Theorem 1.2 we can obtain (3) to (10). Since F and G share 1 CM, by Lemma 2.3, we have
Hence from (3) to (10) and (12) to (14), we get
Hence
, which contradicts that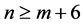
. Proceeding in the same way as in Theorem 1.2, we get
.
Acknowledgements
The author would like thank Prof. S. S. Bhoosnurmath for his valuable suggestions for the improvement of the paper. This research was supported by the UGC under MRP(S).