FDTD Modeling of Lorentzian DNG Metamaterials by Auxiliary Differential Equation Method ()
1. Introduction
Mediums having simultaneously negative permittivity and permeability known as left handed materials (LHM), as conceptualized by Veselago in 1968 [1] , has found numerous applications in microwave circuits and antenna. The LHMs provide some unfamiliar and noteworthy phenomena like negative refraction, reversal of Doppler Effect and Cerenkov radiation etc. This has initiated development of efficient numerical techniques to analyze electromagnetic wave propagation in such left-handed media. The Finite Difference Time Domain (FDTD) method [2] , is an efficient and robust technique which is widely used for modeling electromagnetic wave interaction with various frequency dispersive and non-dispersive materials successfully. The existing frequency dispersive FDTD methods can be broadly classified into three classifications: the Recursive Convolution (RC) method, the Auxiliary Differential Equation (ADE) method and Z-transform method.
In 1990, Luebbers et al. proposed the first frequency dependent FDTD formulation for the modeling of Debye media [3] using the RC method and also used to study wave propagation for Drude materials [4] and Nth order dispersive media [5] . In 2008, D. B. Ge analyzed electromagnetic propagation through dispersive [6] and lossy mediums [7] , implementing FDTD. The bi-isotropic or Chiral media was also investigated using RC-approach [8] in 2004.
Kashiwa and co-workers first used ADE method to formulate Debye media, Lorentz media and Cole-Cole dispersive media [9] -[12] in 1990. Joseph et al. [13] and Gandhi et al. [12] -[14] independently developed an ADE model of Debye media and Nth order dispersive media respectively. A nonlinear phenomenon of dispersive media was investigated by Taflove [15] at the same time.
Z-transforms [16] [17] based on dispersive FDTD formulation was studied first by Sullivan in 1992. Feise et al. [18] proposed Pseudo-Spectral Time Domain (PSTD) technique for the modeling of backward-wave metamaterial and Lee et al. [19] investigated the effective medium approach to modeling split ring resonator LHMs using PLRC method. Ziolkowski also investigated the wave propagation in Drude type [20] and Lorentz type [21] LHMs media in 2001. Chen et al. [22] implemented Z-transform to model Lorentzian DNG metamaterials in FDTD ground in 2004. Then a lot of work has been done in this field. At its very latest, in 2011, K.H. Lee implemented FDTD method on Lorentz-Drude Dispersive Model [23] .
For the truncation of computational domain, the MUR boundary condition and the Perfectly Matched layers (PMLs), invented by Berenger [24] could absorb waves at all frequencies as well as all angles for the linear, anisotropic and other complicated mediums. In 2000, Roden and Gedney invented the CPML (Convolution PML) [25] , which was applicable to complex media including anisotropic media. CPML can also be referred to as Complex frequency shifted PML (CFS-PML) as frequency shifting is accomplished in the argon plane. CPML boundary is also implemented for Lorentzian DNG Metamaterial formulation by Auxiliary Differential Equation Based ADI-FDTD [26] .
In this paper, the formulation of ADE scheme for FDTD formulation in normal DPS as well as DNG based materials is carried out. Section 2 deals with the formulation of ADE method for metamaterials media and followed by boundary condition of MUR and CPML formulation in Section 3; the numerical results of 1-D and 2-D case are discussed in Section 4. The concluding remarks are given in Section 5.
2. ADE Formulation of DNG Metamaterial
2.1. Discrete Maxwell’s Equations and FDTD
The time-dependent Maxwell’s curl equations that are indispensable in FDTD formulation are given in (1) and (2), respectively.
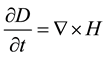 (1)
(1)
 (2)
(2)
For simplification of the problem, it is assumed that the wave propagates through a vacuum medium. Additionally, the cells of the domain have been assumed to be of the same size. The electromagnetic-field components are arranged on the cells in the same way as that using the conventional FDTD method. Taking the central difference approximations, for both the time and space co-ordinates, we get the FDTD formulations.
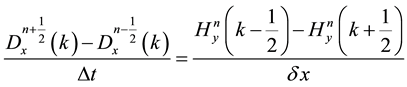 (3)
(3)
 (4)
(4)
where  is the space increment and
is the space increment and  the time step.
the time step.
The equations shown above allow updating of both the electric and magnetic field in the DPS region; however the formulation changes in the DNG region.
 (5)
(5)
 (6)
(6)
 and
and  are such chosen so that at a certain frequency, these parameters become negative, hence modeling the layer DNG.
are such chosen so that at a certain frequency, these parameters become negative, hence modeling the layer DNG.
2.2. The Metamaterial Region
The equation governing the formulation of the metamaterial region are given as in [13]
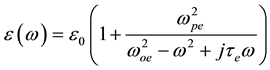 (7)
(7)
 (8)
(8)
where 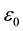 and
and  are the free space permittivity and permeability,
are the free space permittivity and permeability, 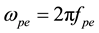 and
and  are the electric and magnetic plasma frequency,
are the electric and magnetic plasma frequency, ![]() and
and ![]() are the low frequency edge of electric and magnetic forbidden band,
are the low frequency edge of electric and magnetic forbidden band, ![]() and
and ![]() are the electric and magnetic collision frequency.
are the electric and magnetic collision frequency.
Now, for calculation of fields in this layer, an inverse Fourier Transform (IFT) to change the s-domain equations into time domain auxiliary differential equations is used. It is further reduced to recursive formulations by the central difference approximation method and hence the fields are updated by time marching algorithm. A new parameter ![]() is introduced in the formulation.
is introduced in the formulation.
![]() (9)
(9)
where![]() (10)
(10)
or ![]() (11)
(11)
By using the conversion ![]() and
and![]() , and by denoting
, and by denoting
![]() as
as![]() , by recursion in time domain we finally get the updated equations,
, by recursion in time domain we finally get the updated equations,
![]() (12)
(12)
Arranging like terms, we get,
![]()
or,![]() (13)
(13)
Thus, we obtain ![]() by this formulation.
by this formulation.
Similarly converting (9) into time domain by IFT method we get,
![]() (14)
(14)
Finally, by the above formula we obtain the electric field in the time domain for the DNG slab region.
3. Boundary Conditions for 1-D and 2-D
To deal with open domain sources, some boundaries are needed as mentioned above to restrict the reflection of the outgoing source waves.
3.1. Absorbing Boundary Conditions (Mur’s ABC)
The ABCs have been used for their easier implementation in the 1-D problem space. At the boundaries, it takes double time steps for a wave front to cross the cell. Since boundaries have been given at both ends, need both upper and lower boundary conditions in order to implement the above situation. The fields are updated accordingly keeping in mind that consistency is maintained throughout the Yee cell. The formulation code used is
![]() (15)
(15)
3.2. Convolution Perfectly Matched Layer (CPML)
The Mur’s ABC is inefficient and inaccurate for 2-D problem space simulation. In such situations an improve version of Beranger’s PML, the CPML (Convolution PML) is introduced by Roden and Gedney in 2000. CPML is applicable to general media including anisotropic media, while implementing the splitting field technique also. CPML can also be referred to as Complex frequency shifted PML (CFS-PML) as frequency shifting is accomplished in the argon plane. The final electric field components can be expressed as:
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
These codes are implemented in MATLABTM and simulated to obtain the results for both 1-D and 2-D cases. The code contains various parameters, iterations and matrices that are needed to update the necessitated fields. The simulation was performed in an Intel Core I3 processor, 300 GB Memory, 3 GB RAM using MATLABR2010 version.
4. Numerical Results and Discussions
In this section the 1-D and 2-D numerical results of the above formulation are represented.
4.1. One Dimensional Case
In case of one dimensional, the medium is considered as Figure 1; where the DNG slab is inserted between the two DPS (ε > 0, μ > 0) layer. To formulate the DNG layer, the following data are considered.
![]()
The negative unity value arises for permittivity and permeability when![]() . The problem space is considered to be of 300 cells.
. The problem space is considered to be of 300 cells. ![]() is chosen as 0.0377,
is chosen as 0.0377, ![]() from the Courant condition, where c denotes speed of light.
from the Courant condition, where c denotes speed of light.
The DNG slab is interjected from cell no. 120 to cell no. 180, between two DPS slabs each of 120 cells. The rest of the problem space consider as free space. Mur’s Absorbing Boundary condition (ABC), which is very efficient for the case of 1-D problem, is applied at the ends to truncate the problem space.
The Gaussian modulated pulse, whose central frequency equal to ωpeak , parameters spread as 30 and delay as 5, is launched 5 cells from the left boundary of the DPS 1 region.
Comparative study is made between DNG and DPS region where the DNG region of the Figure 1 is replace by DPS (actually it is DPS2 as shown in Figure 2(a)) region with permittivity of 2 which is basically normal dielectric region. The snap shot of electric field distribution at 4995th time step for DPS-DPS-DPS interface and DPS-DNG-DPS interface are shown in Figure 2(a) and Figure 2(b) respectively. A distinguishable comparison from the snap shot is observed for the normal incident of wave. The amplitude of the electric field gradually increases when the wave approach towards the DNG region. It signifies that the DNG medium has a capability to increase the energy of the wave compared to normal DPS region.
![]()
Figure 1. Geometry of 1-D DPS-DNG-DPS problem space where wave propagation along x direction.
![]() (a)
(a)![]() (b)
(b)
Figure 2. Wave electric field distribution at time step t = 4995th (a) the DPS-DPS-DPS interface (b) the DPS-DNG- DPS interface.
The time histories of the electric field recorded at two specific points within the DNG medium, one at the center of the DNG medium (x = 150∆x) and another at 20 cells ahead (x = 130∆x) from the center. The electric field profile ![]() and
and ![]() are recorded for early time and delay time as shown in Figure 3(a) and Figure 3(b) respectively. It is observed that the early time response at point 1 is occurs before the point 2. This shows that causality in the direction of the wave propagation is preserved in the DNG medium, which is in agreement with the results presented in [20] . Another interesting property observed in Figure 3 is that the response at the second point leads the one at the first point in the delay time
are recorded for early time and delay time as shown in Figure 3(a) and Figure 3(b) respectively. It is observed that the early time response at point 1 is occurs before the point 2. This shows that causality in the direction of the wave propagation is preserved in the DNG medium, which is in agreement with the results presented in [20] . Another interesting property observed in Figure 3 is that the response at the second point leads the one at the first point in the delay time
4.2. Two Dimensional Case
![]() (a)
(a)![]() (b)
(b)
Figure 3. Time histories of FDTD electric field at the x = 150∆x center of the DNG slab and at x = 130∆x, 20 cells ahead from the center (a) for early-time results; (b) for delay-time results.
![]()
Figure 4. Geometry of DNG embedded 2-D problem space implementing CPML.
The interaction of TM wave with DNG slab is display in Figure 5 at different time instants. The wave is launch from DPS region, 3 cells before the CPML boundary. The wave is incident normally to the DNG slab and after entering the DNG region, the backward wave propagation is observed, which is one of the characteristics of left-handed metamaterial. Again forward propagation of the wave is observed when it reaches at the second DPS region.
5. Conclusion
The FDTD formulations incorporated with auxiliary differential equation method is presented for modeling the Lorentzian DNG metamaterial. The effectiveness of ADE method is established for the case of complex media. Mainly two properties of the metamaterial are discussed in 1-D and 2-D FDTD formution. The DNG metamaterial has capability to increase the amplitude of field component, compared to normal dielectric media, when the wave is passed through it which is observed from 1-D simulations. The causality is also maintained throughout the metamaterial layer and the energy gets absorbed in DNG medium from the surrounding media and hence behaves as a secondary energy source. The 2-D results demonstrate the backward propagation of wave in DNG media. An improvement over the conventional PML, CPML has been used here as efficient boundary conditions. As, the PML is inefficient in absorbing evanescent waves, the source must be placed faraway from the
![]() (a) (b)
(a) (b)![]() (a) (b)
(a) (b)
Figure 5. Electric field distribution at different time step of 2-D DPS-DNG DPS interface (a) at t = 75∆t, (b) at t = 250∆t, (c) at t = 359∆t, (d) at t = 855∆t.
boundary. This increases the number of cells and hence computational requirements and memory. Our results demonstrate that CPML performs very well even with the source being introduced close to the boundaries. Also PML recoreds late time reflections due to its weak causal nature. Specially, the 2-D implemention for a metamaterial is very difficult for PML as PML takes into account a continous function all throughout the region. CPML being strictly causal has no problem regarding evanescent waves and hence, source is placed very close to the boundaries, thus saving memory [8] .