Fine Structure Analysis of the Configuration System of V II. Part I: Even-Parity Levels ()
1. Introduction
The early successful fs analysis of the V II spectrum was due to Meggers and Moore [1] . According to their classification, all except two of the terms were known in the configurations 3d34s and 3d4, but 3d24s2 was altogether unknown. Later, Sugar and Corliss compiled the energy levels of vanadium in its 23 stages of ionization, which were analysed from atomic spectra [2] . Iglesias [3] added 30 new levels to those already published for the 3d34d configuration, using 149 lines, classified as 3d34p - 3d34d transitions. Up to now, no parametric analysis of hfs exists for any even or odd configurations of V II. We propose to fill this absence, as we did previously for many singly ionized atoms: Hf II, Zr II, Ta II, Ti II and Nb II [4] - [8] in an aim to complete previous works and to eliminate erroneous level assignments. The background and motivation of this work should present high interest for astrophysical investigations, very useful in the study of the history of nucleosynthesis, chemically peculiar stars and the sun.
2. Accurate Fine and Hyperfine Structure Analysis
As only a few lowest energy configuration even-parity levels were available from experimental data, in our previous works regarding the fs of transition metal elements much of our analyses of model spaces were restricted to (3d + 4s)4, (4d + 5s)4 and (5d + 6s)4. Fortunately, the energy levels of the five lowest configurations for V II are determined experimentally [1] [3] . We also know that there is poor isolation of the configurations (3d + 4s)4 from other configurations in the 3d-elements since some of their levels are located above the levels belonging to other even-parity configurations whose centers of gravity positions are higher.
Therefore, we use a configuration basis set, called the extended model space, which consists of the following six configurations: (3d + 4s)4 + 3d35s + 3d34d + 3d35d. The interactions between particular states are determined quantitatively by this analysis. The complete details of fs analysis were already given in our previous papers: see for instance [8] .
The fs least squares fitting procedure has been carried out for over 170 energy levels attributed to the extended model space. Table 1 lists the observed energy levels, calculated eigenvalues, and percentages of the largest and next largest wave function components with the corresponding LS term designations. A set of 37 parameters selected among a total of 157, requisite for fs analysis, treated as free, concern only configurations with known experimental levels, i.e. 3d24s2, 3d34s, 3d4, 3d34d and 3d35s in this work.
The fitted values of these parameters are given in Table 2 and Table 3 with their uncertainties in parentheses; the agreement was improved by taking into account the interactions between all known configuration energy levels. For comparison we have inserted also ab initio calculations using the Cowan code [9] . A fit with a standard deviation of 55 cm−1 has been achieved. This fit may be considered as good, considering the large number of degrees of freedom: 132 = 169 − 37. The other parameters with significant values are fixed to their weighted ab initio values while those expected to be small, although predicted by theory, are fixed to zero and then are not listed in these two tables. We confirm on the whole the attributions to term designations given previously [1] - [3] except in two cases: two triplet positions, 3d3( 2 F )4s c 3F and 3d4d 3F , located at 30,300 cm−1 and 30600 cm−1. We propose to invert these two triplet positions as we did in Table 1. It has been brought immediately to our attention by experimental hfs data given in Table 1 of Ref. [10] since when comparing A values for J = 2 and J = 3 one can notice A values for 3d3( 2 F )4s c 3F are smaller than those of 3d4 d 3F and 3d4 b 3F which means broadly that the magnetic contribution of an s-contact-electron is less important than that of a d-electron. We propose moreover to correct the wrong position of the singlet 3d24s2 1D2 which must be rather lower than 3d34s 2D; 3D, i.e. 44,104 (40) cm−1 instead of 44,657 cm−1.
Let us point out that all parameters except spin-orbit ζnd and energies of configuration centers of gravity Eav
are weighted by a factor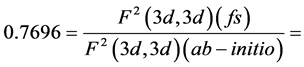 , i.e. the ratio between Slater integrals F2(3d, 3d)
, i.e. the ratio between Slater integrals F2(3d, 3d)
for the 3d34s configuration obtained thanks to the fs study and ab initio calculations, as we did previously [4] - [8] . In Table 4 we give up to 100,000 cm−1 our predicted data for missing experimental energies for these five configurations, analysed in [1] - [3] . This will surely help further experimental V II work to complete this ion study.
Concerning the hfs analysis we follow the many-body parametrisation method [11] which allows us to take advantage of similarities between configuration interaction effects observed independently in spin-orbit and hyperfine splitting. The radial parameters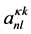 ,
,  , ai and bi have been evaluated by fitting them to experimentally determined hfs constants A and B using the theoretical expressions (Equations (4) and (5) of [12] for instance).
, ai and bi have been evaluated by fitting them to experimentally determined hfs constants A and B using the theoretical expressions (Equations (4) and (5) of [12] for instance).
In 2011, Armstrong, Rosner and Holt applied fast-ion-beam laser-fluorescence spectroscopy to measure with good accuracy the magnetic dipole hfs A constants of 24 even levels and 31 odd levels of 51V II [10] which are the first published data for hfs of this ion.
A: 3d24s2 configuration; B: 3d34s configuration; C: 3d4 configuration; K: 3d35s configuration; L: 3d36s configuration; M: 3d34d configuration; N: 3d35d configuration; *See text.
![]()
Table 2. Fine structure fitted parameters values (in∙cm−1) for the even-parity levels of V II (Fit) with their uncertainties in parentheses and for comparison their corresponding ab initio values computed by means of the Cowan code (C.C.). See also text.
aFixed to the fitted value.
![]()
Table 3. Fine structure configuration interaction parameters and for comparison their corresponding ab initio values computed by means of the Cowan code (C.C.).
![]()
![]()
![]()
Table 4. Predicted singlet, triplet and quintet positions for missing experimental energy levels of the configurations mentioned in Table 2.
A.G.E.: already given experimentally.
A good fit, with a root mean square uncertainty of 6.2 MHz was obtained. The values of the model space hfs parameters, quoted with their uncertainties, are presented in Table 5. In order to check the validity of these fitted parameters we have compared some of them to those computed using values obtained by means of the Cowan
code. For example one can use the well-established relation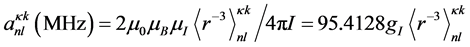 .
.
Using the values of line 2 of Table 6, knowing that the nuclear spin and magnetic dipole moment of 51V are equal respectively to 7/2 and 5.1485 μn one gets the  values of line 3 of Table 6 which are on the whole close to the experimental ones, located in line 1 of the same Table. This confirms the well-founded basis of our work.
values of line 3 of Table 6 which are on the whole close to the experimental ones, located in line 1 of the same Table. This confirms the well-founded basis of our work.
To check the value of the most influential hfs-deduced parameter,  , it is interesting to compare the ratio
, it is interesting to compare the ratio ![]() relative to V I [13] and V II (this work) with
relative to V I [13] and V II (this work) with ![]() relative to Ti I [14] and Ti II [7] . Since these ratios are very close for these two neighbour elements in the Peri-
relative to Ti I [14] and Ti II [7] . Since these ratios are very close for these two neighbour elements in the Peri-
odic Table, we can conclude that the deduced ![]() value for V II is really satisfactory. To extract magnetic dipole A-values from experimental hfs splitting the electric quadrupole hfs B factors preferably were fixed deliberately to zero in [12] because the electric quadrupole moment of 51V is small: −0.05b. In this case it is not useful to compute
value for V II is really satisfactory. To extract magnetic dipole A-values from experimental hfs splitting the electric quadrupole hfs B factors preferably were fixed deliberately to zero in [12] because the electric quadrupole moment of 51V is small: −0.05b. In this case it is not useful to compute ![]() values since it is not possible to make comparisons between experimental and theoretical
values since it is not possible to make comparisons between experimental and theoretical ![]() values.
values.
In Table 7 we have listed the measured hfs constants A given in MHz, used in our fitting procedure. In this
![]()
Table 5. The fitted hfs many-body parameter values in MHz for the model space (3d + 4s)4. The uncertainties given in parentheses are the standard deviations.
a4 = a5 = a6 = a7 = a8 = a10 = 0.00 (fixed).
![]()
Table 6. Comparison between fitted and calculated hfs many-body parameter ![]() in MHz. Radial integrals are computed by means of the pseudo-relativistic Cowan code.
in MHz. Radial integrals are computed by means of the pseudo-relativistic Cowan code.
![]()
![]()
Table 7. Our computed hfs A-constants of V II (in MHz), compared with those obtained experimentally by Armstrong et al. [10] .
*: See text.
Table we inserted also our computed values which confirm totally the Armstrong, Rosner and Holt experimental data [12] which are sometimes different from those of Arvidsson [15] . As regards the 3d24s2 e 3F4 (38517.06 cm−1) hfs value we reject A= −351.28 and we keep A= 276.67 MHz since two values were proposed in [12] (owing to an unavoidable ambiguity in ΔJ = 0 transitions).
3. Conclusion
Parametric fs studies including configuration interactions have been carried out for five interacting configurations of V II. We furthermore propose predicted energy level values for missing experimental ones up to 100,000 cm−1 for further investigations. One can also note that calculated Landé gJ-factors were also in good agreement with the experimental ones. Unfortunately the latter are not as numerous as we might have expected and thus our work to check level assignments became more difficult. We give for the first time the hfs many- body parameter values with good accuracy for the model space (3d + 4s)4, taking advantage of the accurate work done in [10] . This provides better predictions for still unknown levels. The conclusive comparison between the experimental and calculated hfs A-constants, given in Table 7, provides a good check on the quality of the wave functions obtained by the least squares fit of the fine structure, used to determine the expansions of hfs A-constants in intermediate coupling. Very recently the spectrum of V II has been recorded by FTS and thirty- nine of the additional eighty-five high levels published by Iglesias et al. [3] have been confirmed or revised, and four of their missing levels have been found [16] as regards even-parity levels. One can note in our Table 1 a total agreement with the assignments of these four new levels given in this interesting work.