Some Fixed Point Results of Ciric-Type Contraction Mappings on Ordered G-Partial Metric Spaces ()
1. Introduction and Preliminary Definitions
The Banach contraction principle has been generalized and extended in many directions for some decades. Of all the generalizations, Ciric [1] [2] generalizations seem outstanding. Cho Song Wong [3] dealt with a pair of operators in which the control functions in the generalized contraction maps are upper semi-continuous, while Ciric considered a single operator and took the control function to be a constant. If the control function is an upper semi-continuous, then the result of Ciric [1] is invalid. In Kiany and Amini-Harandi [4] , a condition is imposed on the control function and the mapping is termed a Ciric generalized quasi-contraction mapping. In this work, we introduce the concept of generalized quasi-contraction mappings in the new framework of G-partial metric spaces.
Rodriguez-Lopez and Nieto [5] , Ran and Reuring [6] presented some new results for the existence of the fixed point for some mappings in partially ordered metric spaces. The main idea in [5] [6] involves combing the ideas of an iterative technique in the contraction mapping principle with those in the monotone technique. In this work, the existence of a unique fixed point for generalized contraction mappings in ordered G-partial metric spaces is proved.
Matthew [7] generalized the notion of metric spaces by introducing the concept of nonzero self-distance and thus, defined a generalized metric space known as partial metric space, as follows:
Definition 1.1. [7] . A partial metric space is a pair (X, p), where X is a nonempty set and  such that:
such that:
(p1) 
(p2) if  then
then 
(p3) 
(p4) 
He was able to establish a relationship between partial metric spaces and the usual metric spaces when
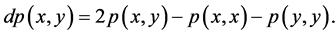
Mustafa and Sims [8] also extended the concepts of metric to G-metric by assigning a positive real number to every triplet of an arbitrary set as follows:
Definition 1.2. [8] . Let X be a nonempty set, and let
 be a function satisfying:
be a function satisfying:
(G1) 
(G2)  for all
for all 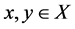 with
with 
(G3) 
(G4)  (symmetry in all three variables)(G5)
(symmetry in all three variables)(G5)  for all
for all  (rectangle inequality).
(rectangle inequality).
Then, the function G is called a generalized metric, or more specifically, a G-metric on X, and the pair  is a G-metric space.
is a G-metric space.
Mustafa [8] gave an example to show the relationship between G-metric spaces and ordinary metric spaces as: For any G-metric G on X, if  then
then  is a metric space.
is a metric space.
In this work, the idea of the nonzero self-distance of partial metric spaces and the rectangle inequality of G-metric spaces are combined to develop a new generalized metric space which is defined as the following:
Definition 1.3. Let X be a nonempty set, and let 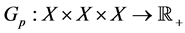 be a function satisfying the following:
be a function satisfying the following:
(Gp1)  (small self-distance)(Gp2)
(small self-distance)(Gp2) 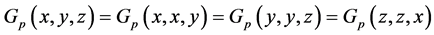 iff
iff 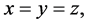 (equality)(Gp3)
(equality)(Gp3)  (symmetry in all three variables)(Gp4)
(symmetry in all three variables)(Gp4)  (Rectangle inequality).
(Rectangle inequality).
The function  is called a G-partial metric and the pair
is called a G-partial metric and the pair  is called a G-partial metric space.
is called a G-partial metric space.
Definition 1.4. A G-partial metric space is said to be symmetric if  for all
for all .
.
In this work, we will assume that  is symmetric. The following proposition establishes the relation between G-partial metric spaces and (partial) metric spaces.
is symmetric. The following proposition establishes the relation between G-partial metric spaces and (partial) metric spaces.
Definition 1.5. Let  be a G-partial metric space. Define the functions
be a G-partial metric space. Define the functions  and
and  by
by  and
and  Then 1) (X, p) is a partial metric space.
Then 1) (X, p) is a partial metric space.
2) (X, d) is a metric space.
Proof 1) From (Gp1), we have that for all 

hence (p1) is satisfied.
If 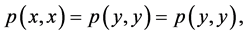 then
then

By (Gp1), it must follow that 
From the symmetry of  and by (Gp2),
and by (Gp2), 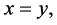 hence (p2) is satisfied.
hence (p2) is satisfied.
(p3) follows from (Gp3) and the triangle inequality (p4) is easily verifiable using (Gp4).
2) Since (X, p) is a partial metric space, then

defines a metric on X and so  also defines a metric on X.
also defines a metric on X.
Example 1.6. Let 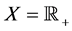 and define the function
and define the function  as
as 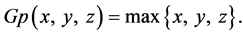 Then
Then 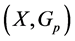 is a G-partial metric space.
is a G-partial metric space.
We state the following definitions and motivations.
Definition 1.7. A sequence  of points in a G-partial metric space
of points in a G-partial metric space  converges to some
converges to some  if
if 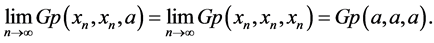
Definition 1.8. A sequence  of points in a G-partial metric spaces
of points in a G-partial metric spaces  is Cauchy if the numbers
is Cauchy if the numbers  converges to some
converges to some  as n, m, l approach infinity.
as n, m, l approach infinity.
The proof of the following result follows from the above definitions:
Proposition 1.9. Let  be a sequence in G-partial metric space X and
be a sequence in G-partial metric space X and . If
. If  converges to
converges to  then
then 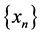 is a Cauchy sequence.
is a Cauchy sequence.
Definition 1.10. A G-partial metric space 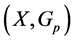 is said to be complete if every Cauchy sequence in
is said to be complete if every Cauchy sequence in  converges to an element in
converges to an element in .
.
Definition 1.11. [6] . If 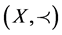 is a partially ordered set and T: X → X, then T is monotone non-decreasing if for every
is a partially ordered set and T: X → X, then T is monotone non-decreasing if for every ,
,  implies
implies .
.
Definition 1.12. Let 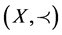 be a partially ordered set. Then two elements
be a partially ordered set. Then two elements  are said to be totally ordered or ordered if they are comparable, i.e.
are said to be totally ordered or ordered if they are comparable, i.e.  or
or .
.
Gordji et al. [9] proved the existence of a unique fixed point for contraction type maps in partially ordered metric spaces using a control function. Kiany and Amini-Harandi [4] proved the existence of a unique fixed point for a generalized Ciric quasi-contraction mapping in what they tagged a generalized metric space. The map they considered extend that of Gordji et al., albeit the space they considered was not endowed with an order. Saadati et al. [10] considered the concept of Omega-distances on a complete partially ordered G-metric space and proved some fixed point theorems. Turkoglu et al. [11] and Sastry et al. [12] proved some fixed point theorems for generalized contraction mappings in cone metric spaces and metric spaces respectively.
In this work, the existence of unique fixed points of the two generalized contraction mappings below is proved in ordered G-partial metric spaces, extending thus the results in [2] [4] [9] [11] .
Definition 1.13. Let  be a G-partial metric space. The self-map T: X→ X is said to be a generalized Ciric quasi-contraction if
be a G-partial metric space. The self-map T: X→ X is said to be a generalized Ciric quasi-contraction if
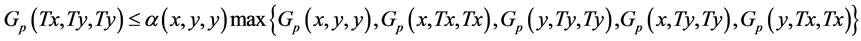 (1)
(1)
for any  where
where  is a mapping.
is a mapping.
Definition 1.14. Let  be a G-partial metric space. The self-map T: X→ X is said to be a generalized G-contraction if for all
be a G-partial metric space. The self-map T: X→ X is said to be a generalized G-contraction if for all 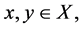
 (2)
(2)
where  are functions such that
are functions such that

2. Main Results
Theorem 2.1. Let  be a partially ordered set and suppose there exists a G-partial metric
be a partially ordered set and suppose there exists a G-partial metric 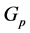 in X such that
in X such that 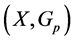 is a complete G-partial metric space. Let
is a complete G-partial metric space. Let  be a self-mapping in X such that for each
be a self-mapping in X such that for each  satisfying
satisfying 
 (3)
(3)
where  are functions such that
are functions such that
 (4)
(4)
Suppose T is a non-decreasing map such that there exists an 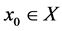 with
with . Also suppose that X is such that for any non-decreasing sequence
. Also suppose that X is such that for any non-decreasing sequence  converging to x,
converging to x, 
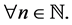
 for all
for all 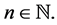
Then T has a fixed point. Moreover, if for each , there exists
, there exists  which is comparable to u and v, then T has a unique fixed point.
which is comparable to u and v, then T has a unique fixed point.
Proof. Fix 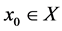 Let
Let 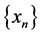 be defined by
be defined by  ,
,  , ···,
, ···, . Since
. Since 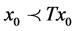 and T is non-decreasing, then
and T is non-decreasing, then 
This implies that  for each
for each .
.
Since 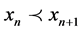 for each
for each  then by (3) we have
then by (3) we have

Thus, with  evaluated at
evaluated at , we have
, we have
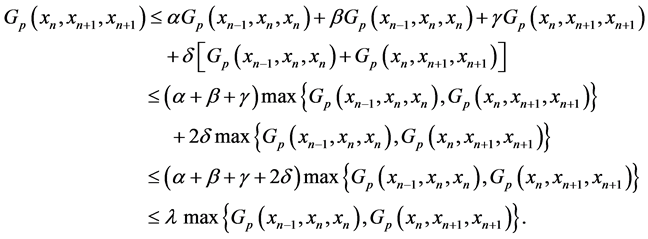 (5)
(5)
Since  then (5) becomes
then (5) becomes 
Consequently, 
For 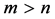 we get,
we get,
 (6)
(6)
Take the limit as  in (6) yields
in (6) yields  which implies that
which implies that  is a Cauchy sequence. Since X is a complete space then there exists
is a Cauchy sequence. Since X is a complete space then there exists  such that
such that  converges to
converges to  and
and

Next we prove that  is the fixed point of T. From (3) and (4), since
is the fixed point of T. From (3) and (4), since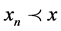 , for all
, for all ,
,

where  are evaluated at
are evaluated at 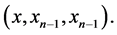
Take limit as 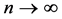 yields
yields

Since  then
then  Hence
Hence 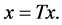
For uniqueness, suppose  and
and 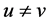 are two fixed points of T, and there exists
are two fixed points of T, and there exists 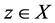 which is comparable to
which is comparable to 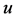 and
and  Monotonicity of T implies that
Monotonicity of T implies that  is comparable to
is comparable to 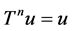 and
and 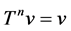 for
for .
.
Moreover

where  are evaluated at
are evaluated at 
Taking the limit as  and by symmetry we get,
and by symmetry we get,
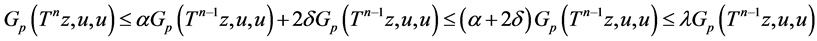 (7)
(7)
Consequently, 
Similarly, 
Finally for all  with
with  where
where  we have,
we have,
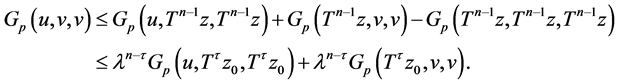
Letting  yields
yields 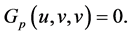 Hence
Hence 
Theorem 2.1 can be viewed as an extension of results of Turkoglu et al. ([11] , Theorem 2.1) to the setting of G-partial metric spaces endowed with an order. The following corollary can be obtained:
Corollary 2.2. Let  be a partially ordered set and let there exist a G-partial metric
be a partially ordered set and let there exist a G-partial metric  in X such that
in X such that  is a complete G-partial metric space. Let
is a complete G-partial metric space. Let  be a self-mapping in X such that for each
be a self-mapping in X such that for each  satisfying
satisfying 
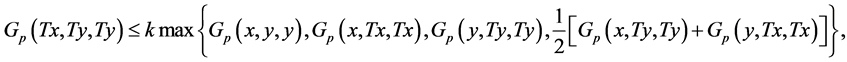
where 
Suppose T is a non-decreasing map such that there exists an  with
with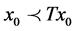 . Also suppose that X is such that for any non-decreasing sequence
. Also suppose that X is such that for any non-decreasing sequence  converging to
converging to ,
,  for all
for all  Then T has a fixed point. Moreover, if for each
Then T has a fixed point. Moreover, if for each 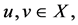 there exists
there exists  which is comparable to
which is comparable to  and
and 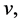 then T has a unique fixed point.
then T has a unique fixed point.
Proof: Observe that

where  and
and  are chosen such that for any
are chosen such that for any 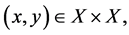 one and only one of
one and only one of  is non-null. In such case,
is non-null. In such case,

Thus, the proof of the corollary follows from Theorem 2.1.
Theorem 2.3. Let  be a partially ordered set and suppose there exists a G-partial metric
be a partially ordered set and suppose there exists a G-partial metric  in X such that
in X such that  is a complete G-partial metric space. Let
is a complete G-partial metric space. Let 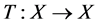 be a generalized Ciric quasi-contraction map such that
be a generalized Ciric quasi-contraction map such that  satisfies
satisfies  for each
for each  for any
for any  with
with 
Assume that there exists an  with the bounded orbit, that is the sequence
with the bounded orbit, that is the sequence  defined by
defined by  for all n, is bounded. Furthermore, if T is an increasing map such that there exists an
for all n, is bounded. Furthermore, if T is an increasing map such that there exists an  with
with 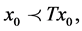 and if any non-decreasing sequence
and if any non-decreasing sequence  satisfies
satisfies 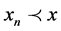 for all n, then T has a fixed point. Moreover, if for each
for all n, then T has a fixed point. Moreover, if for each  there exists
there exists  which is comparable to
which is comparable to  and
and  then T has a unique fixed point.
then T has a unique fixed point.
Proof. Starting with  such that
such that  and with T non-decreasing, we have
and with T non-decreasing, we have

We prove that there exists 0 < c < 1 such that
 (8)
(8)
On the contrary, assume that

for some subsequence  of
of  Since by our assumption the sequence
Since by our assumption the sequence  is bounded, then the subsequence
is bounded, then the subsequence  is bounded too. Since the sequence is monotonic and bounded then it converges. Let
is bounded too. Since the sequence is monotonic and bounded then it converges. Let  From our assumption,
From our assumption, 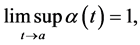 a contradiction. Thus (8) holds.
a contradiction. Thus (8) holds.
Now, we show that  is a Cauchy sequence. To prove the claim, we show by induction that for each
is a Cauchy sequence. To prove the claim, we show by induction that for each 
 (9)
(9)
where K is a bound for the bounded sequence 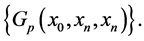 When
When 

From the axiom (Gp1),  Thus
Thus

Thus (9) holds for 
Suppose that (9) holds for each k < n; let us show that it holds for k = n. Since T is a generalized Ciric quasicontraction map,
 (10)
(10)
From axiom (Gp1), 
Hence (10) becomes

From the induction hypothesis,  Thus,
Thus,
 (11)
(11)
We also have from the definition of T and the induction hypothesis,

The inequality (11) becomes
 (12)
(12)
Repeating the same process,

Thus (9) holds for each  From (9) we deduce that
From (9) we deduce that  is a Cauchy sequence.
is a Cauchy sequence.
Since X is complete then there exists  such that
such that  and
and

Now we prove that q is the fixed point of T. To show that, we claim that there exists 0 < b < 1 such that 
On the contrary, we assume 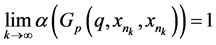 for some subsequences
for some subsequences 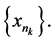 Since
Since  then
then 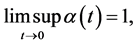 a contradiction.
a contradiction.
Since T is a generalized quasi-contraction mapping we have

Letting  we have,
we have, 
Also . Hence
. Hence  Since b < 1, q = Tq.
Since b < 1, q = Tq.
The uniqueness of the fixed point follows from the quasicontractive condition.
Theorem 2.3 is an extension of Theorem 2.3 of Gordji et al. [4] to G-partial metric space in the sense that, if

in (1), then we get

which is the G-partial metric version of the map of Gordji [9] .
The proof of Corollary 2.4 follows from Theorem 2.3.
Corollary 2.4. Let 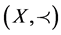 be a partially ordered set such that there exists a G-partial metric on X such that
be a partially ordered set such that there exists a G-partial metric on X such that  is a complete G-partial metric space. Let
is a complete G-partial metric space. Let  be an increasing mapping such that there exists
be an increasing mapping such that there exists 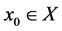 with
with  Suppose that there exists
Suppose that there exists  such that
such that

for all comparable 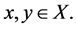 If T is continuous and if for each
If T is continuous and if for each 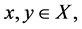 there exists
there exists  which is comparable to x and y. Then T has a unique fixed point.
which is comparable to x and y. Then T has a unique fixed point.
Example 2.5. Let 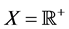 and a G-partial metric defined by
and a G-partial metric defined by 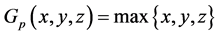 for all
for all  On the set X, we consider the usual ordering
On the set X, we consider the usual ordering  Clearly,
Clearly,  is a complete G-partial metric space and
is a complete G-partial metric space and
 is a partially ordered set. Define a function
is a partially ordered set. Define a function  as follows:
as follows: 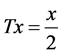 for all
for all  Define
Define 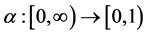 by
by  for each
for each  Then we have,
Then we have,
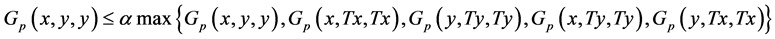
for each  Thus, all of the hypotheses of Theorem 2.3 are satisfied and so T has a unique fixed point (0 is the unique fixed point of T).
Thus, all of the hypotheses of Theorem 2.3 are satisfied and so T has a unique fixed point (0 is the unique fixed point of T).