Bayesian Estimation of Shrubs Diversity in Rangelands under Two Management Systems in Northern Syria ()
1. Introduction
The arid Mediterranean rangelands are known for their high plant species diversity [1] . Due to increased human and livestock population pressure and technological development for exploitation of natural resources, these rangelands are under tremendous threat. The rangelands, established historically as common property resources, are used for grazing by small ruminants, especially sheep and goats. Overgrazing of rangelands by these small ruminants causes degradation [2] -[4] . This results in reduced performance and a gradual reduction in biodiversity and its spatial distribution [5] -[7] . In addition to overgrazing, wind and irregular rainfall make rangelands fragile and vulnerable to top-soil and plant bio-diversity loss. Suitable rangeland management approaches can be implemented to restore or rehabilitate the diversity [8] [9] . Above ground vegetation replenishment depends on aerial seed, rain and viable soil seed banks [10] -[12] . It is essential to study the status of plant biodiversity in the rangelands under various management practices in order to develop recommendations on the preservation of plant diversity.
A study was undertaken at two sites in the Syrian arid rangelands to investigate the effect of range rehabilitation methods on above ground vegetation density and species diversity. Standard diversity indices such as Shannon index of diversity and Simpson reciprocal diversity index are commonly used instead of the observed plant population density and richness [13] -[16] . In context of partitioning the diversity into that at sub-divisions of a larger area, a new weighted Gini-Simpson index which behaves well for partitioning of biodiversity when the number of species is large is introduced in [17] . These measures are based on the frequentist approach. Several factors, which underlie the rangeland environment, affect the emergence, reproduction and identification of the emerged plant species and the diversity of the species in that area. With climate change, the biophysical aspects and weather - especially the drought behavior of the environment - are changing and these changes affect the diversity. Therefore, it is more realistic to consider the prevalence or abundances of the species as random variable rather than assuming a fixed constant. A Bayesian approach, as it is based on distribution of parameters as prior information, is thus more suitable for estimation of the diversity indices. For a set of chosen priors, the objectives of this study were to: 1) describe the diversity in the study regions; 2) estimate the diversity using Bayesian method; and 3) compare the rangeland grazing management treatments for the changes in the diversity.
2. Materials and Methods
2.1. Study Locations
A study was undertaken at two sites located within the Aleppo province between the 35.657372˚N and 37.612917˚E, and 35.611903˚N and 37.499980˚E geographical coordinates. The study was conducted in 2006/ 07 and 2007/08 using the modified Daubenmire quadrat method [18] and the point intercepts method [19] . The areas studied were located within range rehabilitation areas in which continuous, rotational and full protection from grazing methods had been implemented for about 20 years. We present the analysis of data from the two sites and two grazing managements implemented by the Syrian Steppe Directorate, using halophyte shrub transplanting and rotational grazing. At each site and grazing management combination, a representative macro-plot of 3 ha was used for 9 soil samples and grow-out tests were carried out to identify the shrub species and their abundances. The details of the procedures are described by [20] [21] . Table 1 presents the observed distribution of the number of individuals per plant species found at the two sites, Hammam and Obeisan, in Syria and under two contrasting management practices (closed and open system) in 2007.
2.2. Diversity Indices
We estimate the diversity using Shannon and Simpson indices [13] given in the following. In a given year, site (community) and a management system, let there be 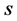 plant species with
plant species with 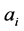 the observed abundance of
the observed abundance of 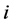 -th species, and
-th species, and 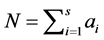 be the observed total number of individual plants of all the species
be the observed total number of individual plants of all the species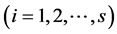 . Further, denote by
. Further, denote by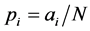 , the proportion of plants belonging to
, the proportion of plants belonging to 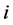 -th species. Let
-th species. Let 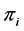 be the true but unknown proportion in the population of the
be the true but unknown proportion in the population of the 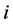 -th species at the site/environment under study
-th species at the site/environment under study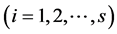 .
.
The Shannon index of diversity is given by 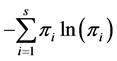 and is estimated by
and is estimated by 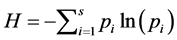 and has a
and has a

Table 1. Distribution of species abundance using growing out method in 2007.
standard error of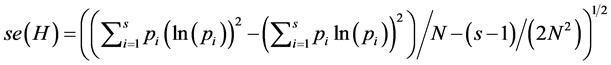 . H can alternately be computed as,
. H can alternately be computed as, 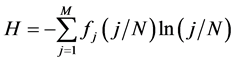 where
where 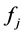 is the number of species appearing
is the number of species appearing 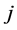 times; M is the maximum number of appearance of any species. Also,
times; M is the maximum number of appearance of any species. Also,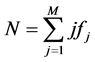 .
.
Another measure, Simpson index of diversity (SID) is given in terms of an index called Simpson’s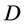 , as
, as 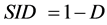 where
where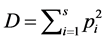 . Standard error of SID,
. Standard error of SID, 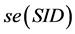 , can be obtained by estimating the square-root of the variance:
, can be obtained by estimating the square-root of the variance:

In the above, the variance and expected values can be expressed in terms of multinomial distribution parameters [22] . The estimates, shown as caps, of various expected values can be given by:

where 
2.3. Bayesian Method and Estimation of Diversity Index
The Bayesian setting requires an estimation of parameters of the proportion of abundance of each species within a system of given number of species and the total abundance (N). Distribution of 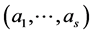 can be seen as multinomial distribution with
can be seen as multinomial distribution with 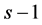 components with
components with 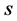 proportions
proportions 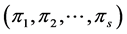 where
where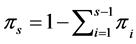 . We briefly describe a Bayesian method for estimation of a single parameter say
. We briefly describe a Bayesian method for estimation of a single parameter say 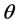 using an observed data vector say
using an observed data vector say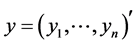 . In our case, e.g.,
. In our case, e.g., 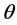 may stand for
may stand for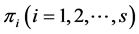 . Let the probability in case of discrete distribution or the likelihood of observing
. Let the probability in case of discrete distribution or the likelihood of observing 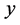 based on a value of the parameter
based on a value of the parameter 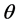 be given by
be given by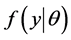 , called likelihood of
, called likelihood of  which is a function of
which is a function of . In Bayesian framework, one introduces a degree of belief in the parameter
. In Bayesian framework, one introduces a degree of belief in the parameter  in terms of its probability distribution function say
in terms of its probability distribution function say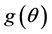 , called a priori distribution of
, called a priori distribution of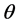 , or, simply a prior for
, or, simply a prior for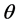 . The inference about
. The inference about 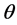 is obtained in terms of the probability distribution of
is obtained in terms of the probability distribution of 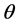 given the data
given the data 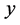 and is expressed as
and is expressed as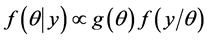 , and called the a posteriori, or simply a posterior, density function of
, and called the a posteriori, or simply a posterior, density function of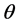 , which is obtainable from the famous Bayes’ Theorem available in standard texts [23] -[25] . Using this a posteriori density, one can obtain the expected value of
, which is obtainable from the famous Bayes’ Theorem available in standard texts [23] -[25] . Using this a posteriori density, one can obtain the expected value of 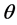 as an estimate of
as an estimate of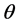 , standard error and its confidence intervals. In case of multiple parameter situation, say
, standard error and its confidence intervals. In case of multiple parameter situation, say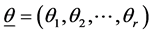 , as is the present case, the generalization of the a posteriori distribution of
, as is the present case, the generalization of the a posteriori distribution of 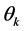 say, based on an assumed joint prior
say, based on an assumed joint prior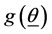 , is given by
, is given by

There are numerical challenges in the evaluation of the multiple integral required in Bayesian estimation, and these challenges are addressed in vast resources of algorithmic tools and computational codes; see, for example, [23] [25] [26] .
In the present context, we proceed as follows. For a fixed N, we assume a multinomial distribution of 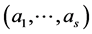 with parameter vector
with parameter vector 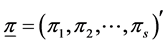 where
where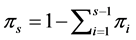 . The probability function of these is given by
. The probability function of these is given by

The marginal distribution of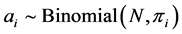 . A Dirichlet distribution is commonly used as a prior for proportions in components of a system. We assume that
. A Dirichlet distribution is commonly used as a prior for proportions in components of a system. We assume that 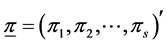 follow
follow 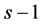 dimensional Dirichlet distribution with parameter vector
dimensional Dirichlet distribution with parameter vector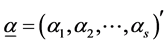 , where
, where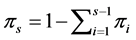 . The a priori probability density function (pdf) of the Dirichlet distribution of the random proportions
. The a priori probability density function (pdf) of the Dirichlet distribution of the random proportions 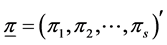 of the i-th species is
of the i-th species is

In above, the random variable and its assumed value is denoted by the same symbol. In this case, it is easy to see that the posterior of 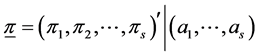 is also a Dirichlet distribution with parameter vector
is also a Dirichlet distribution with parameter vector
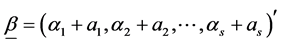 with the pdf given by
with the pdf given by

Thus, the above prior is a conjugate prior. A frequentist estimate of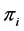 , based on maximum likelihood estimate or method of moments is given by
, based on maximum likelihood estimate or method of moments is given by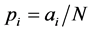 , while an a priori estimate would be
, while an a priori estimate would be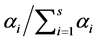 . Using the above prior on
. Using the above prior on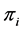 ’s, the a posteriori estimate/expectation of
’s, the a posteriori estimate/expectation of 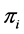 is given by
is given by 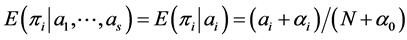 , where
, where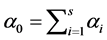 . While the a posteriori distribution of
. While the a posteriori distribution of 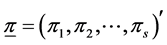 is available in exact form, the a posteriori distribution of H or SID is not. However, its distribution can be simulated using the random values of
is available in exact form, the a posteriori distribution of H or SID is not. However, its distribution can be simulated using the random values of 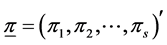 using the Dirichlet distribution with parameter vector
using the Dirichlet distribution with parameter vector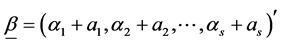 . The expressions for exact mean and variance of the Shannon index has been given by [27] where
. The expressions for exact mean and variance of the Shannon index has been given by [27] where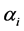 ’s are kept constant. Realizing the fact that a posteriori estimates of
’s are kept constant. Realizing the fact that a posteriori estimates of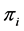 ’s depend on
’s depend on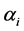 ’s also, it may be worthwhile to allow variation in
’s also, it may be worthwhile to allow variation in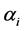 ’s. Since the
’s. Since the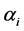 ’s are predetermined known values, we can have various models to choose from. There are many theoretical models for
’s are predetermined known values, we can have various models to choose from. There are many theoretical models for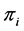 ’s such as random uniform model, geometric series, logarithmic series, broken stick model, Zipf-Mandelbrot model etc. [13] [28] . We therefore take the following three classes of priors for choosing
’s such as random uniform model, geometric series, logarithmic series, broken stick model, Zipf-Mandelbrot model etc. [13] [28] . We therefore take the following three classes of priors for choosing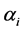 ’ s: 1) constant (
’ s: 1) constant (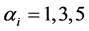 or 10 for all the species), 2)
or 10 for all the species), 2) 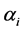 unequal derived as a random sample from uniform (0.5, k) where k = 1, 3, 5, 10, and 3) geometric series and kept within a chosen range given by
unequal derived as a random sample from uniform (0.5, k) where k = 1, 3, 5, 10, and 3) geometric series and kept within a chosen range given by 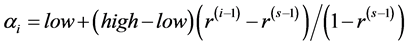 , where the four sets of values (low, high,
, where the four sets of values (low, high,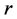 ) were (1, 2, 0.2), (1, 3, 0.2), (1, 3, 0.8), (5, 10, 0.5). The number of simulation runs was taken as 10,000. The computations were carried out using R-language [29] and the codes used are available on request.
) were (1, 2, 0.2), (1, 3, 0.2), (1, 3, 0.8), (5, 10, 0.5). The number of simulation runs was taken as 10,000. The computations were carried out using R-language [29] and the codes used are available on request.
2.4. The Estimates of Diversity Indices
Using the selected values of 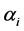 in the Dirichlete distribution as prior parameters to obtain the resulting a posteriori distribution of H and SID, simulations were used to obtain the required probability density function and summary statistics such as mean, median and 95% confidence limits.
in the Dirichlete distribution as prior parameters to obtain the resulting a posteriori distribution of H and SID, simulations were used to obtain the required probability density function and summary statistics such as mean, median and 95% confidence limits.
3. Results
For the four combinations of the sites (Hammam and Obeisan) and grazing methods (Closed, Open), observed number of shrub species were: 23 under the closed area (no grazing), referred to as “Closed”, and 13 under an area open for grazing at Hammam, referred to as “Open”, while at Obeisan, the number of species found were 21 and 20 under Closed and Open grazing systems, respectively (Table 1). The maximum number of abundances varied from 55 to 445 over the four combinations. We simulated the distributions of H and SID based on the prior distribution and posterior distribution of 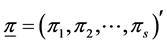 in terms of density plots and mean, standard deviation, skewness, kurtosis and quantiles (data and figures not included). For
in terms of density plots and mean, standard deviation, skewness, kurtosis and quantiles (data and figures not included). For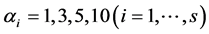 , the a posteriori distributions of H and SID at Hammam showed a shift to the left of their a priori distributions. For
, the a posteriori distributions of H and SID at Hammam showed a shift to the left of their a priori distributions. For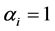 , the a priori distributions covered the range of values of the diversity indices under the a posteriori distribution. The distribution patterns were similar for both the grazing management methods. Thus
, the a priori distributions covered the range of values of the diversity indices under the a posteriori distribution. The distribution patterns were similar for both the grazing management methods. Thus 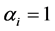 was chosen for the a priori distribution of H and SID. The a priori and a posteriori distributions of the diversity indices were obtained when
was chosen for the a priori distribution of H and SID. The a priori and a posteriori distributions of the diversity indices were obtained when 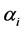 were chosen from as a sample from Uniform (0.5, k) where k = 1, 3, 5, 10. For this site, Hamman, the two distribution curves overlapped reasonably well for all these choices of k. Similarly for values of
were chosen from as a sample from Uniform (0.5, k) where k = 1, 3, 5, 10. For this site, Hamman, the two distribution curves overlapped reasonably well for all these choices of k. Similarly for values of 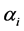 from the geometric series, in majority of cases, the overlap between the a priori and the a posteriori distribution took place for the range of the indices. A wider spread in the a priori distributions was noticed in comparison with the a posteriori distributions.
from the geometric series, in majority of cases, the overlap between the a priori and the a posteriori distribution took place for the range of the indices. A wider spread in the a priori distributions was noticed in comparison with the a posteriori distributions.
3.1. The Choice of αi
Although any of the parameters determining the a priori distribution could be taken, however, to determine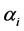 , we identified those parameter values for which the density graphs showed a high degree of overlap with the a priori distribution. Although the data need not determine the a priori distribution, the overlap consideration pointed to the information for choosing a more reasonable prior than taking arbitrarily from a much wider range of priors. The a posteriori probability density of diversity indices are presented for the selected priors in Figures 1-3 and their mean, standard deviation, skewness, kurtosis, quantiles at 2.5%, median and 97.5% in Table 2. Figures 1-3 show that a priori distribution of H/SID has larger skewness and kurtosis compared to the a posteriori distributions. As can be expected, there is a difference between the a priori and a posteriori distributions based on the selected values of
, we identified those parameter values for which the density graphs showed a high degree of overlap with the a priori distribution. Although the data need not determine the a priori distribution, the overlap consideration pointed to the information for choosing a more reasonable prior than taking arbitrarily from a much wider range of priors. The a posteriori probability density of diversity indices are presented for the selected priors in Figures 1-3 and their mean, standard deviation, skewness, kurtosis, quantiles at 2.5%, median and 97.5% in Table 2. Figures 1-3 show that a priori distribution of H/SID has larger skewness and kurtosis compared to the a posteriori distributions. As can be expected, there is a difference between the a priori and a posteriori distributions based on the selected values of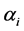 . However, the three a posteriori distributions also showed differences. For Hammam under the Closed grazing system, the mean H and SID varied, over the three priors, in the range 2.60 - 2.62 and 0.91 - 0.92, respectively (Table 2). The 95% confidence intervals for H were (2.51, 2.69), (2.53, 2.61) and (2.53, 2.70) for the three priors
. However, the three a posteriori distributions also showed differences. For Hammam under the Closed grazing system, the mean H and SID varied, over the three priors, in the range 2.60 - 2.62 and 0.91 - 0.92, respectively (Table 2). The 95% confidence intervals for H were (2.51, 2.69), (2.53, 2.61) and (2.53, 2.70) for the three priors 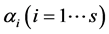 from Uniform (0.5, 3), geometric series (rate = 0.2, low = 1, high = 3) and equal value fixed at 1, respectively.
from Uniform (0.5, 3), geometric series (rate = 0.2, low = 1, high = 3) and equal value fixed at 1, respectively.
3.2. Best Prior
Since the H is a sum of random variables, the central limit theorem supports a normal approximation for its distribution for a large number of species classes. Each a priori distribution results in a posteriori distribution. To provide an estimate, a criterion is needed to select the most suitable distribution out of the posterior distributions considered for a given site and management combination. We took the sum of squares of skewness 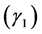 and kurtosis
and kurtosis 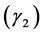 (SSSK) as a criterion,
(SSSK) as a criterion,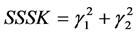 . In case the SSSK is equal for any two posteriors, the preference was given to the low skewness model followed by a low kurtosis. Table 3 summarizes the Bayesian estimates, selected using the SSSK criterion and frequentist estimates of the two diversity estimates for the site and grazing system combinations. Of the four cases, only for one case of Obeisan and Closed system, the same prior, i.e.
. In case the SSSK is equal for any two posteriors, the preference was given to the low skewness model followed by a low kurtosis. Table 3 summarizes the Bayesian estimates, selected using the SSSK criterion and frequentist estimates of the two diversity estimates for the site and grazing system combinations. Of the four cases, only for one case of Obeisan and Closed system, the same prior, i.e. 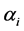 from Uniform (0.5, 1), was found most suitable for the estimation of H and SID indices. In each case, the Bayesian estimates of diversity were slightly higher than their frequentist counterparts and with lower standard error.
from Uniform (0.5, 1), was found most suitable for the estimation of H and SID indices. In each case, the Bayesian estimates of diversity were slightly higher than their frequentist counterparts and with lower standard error.
The two grazing management options were compared for diversity at each of the sites, and the sites were compared for each management using the indices estimated by the Bayesian and frequentist approach. To compare the two indices, we computed p-values based on the normal approximation of the difference of their esti-
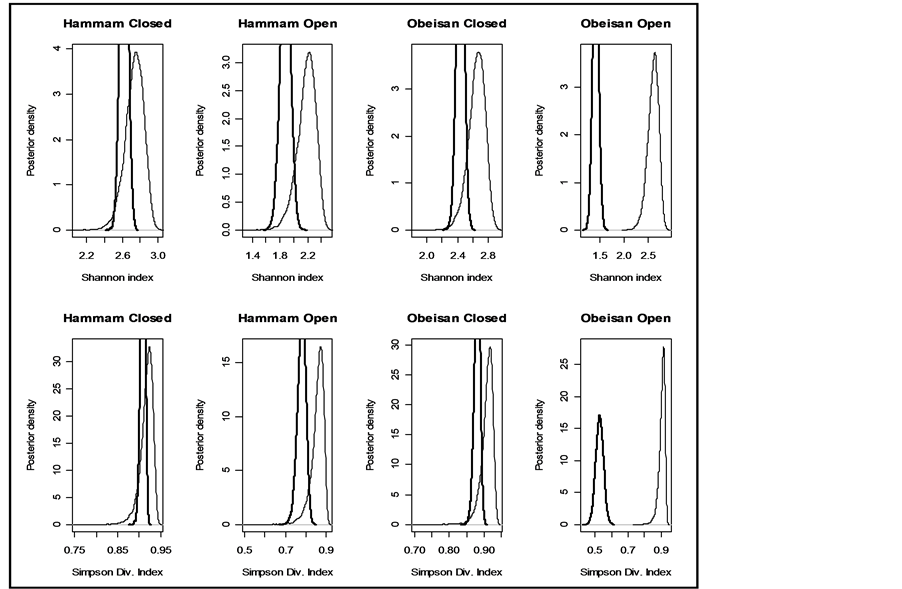
Figure 1. Prior and posterior density of Shannon and Simpson indices for various flattening parameters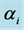 (equal) = 1.
(equal) = 1.
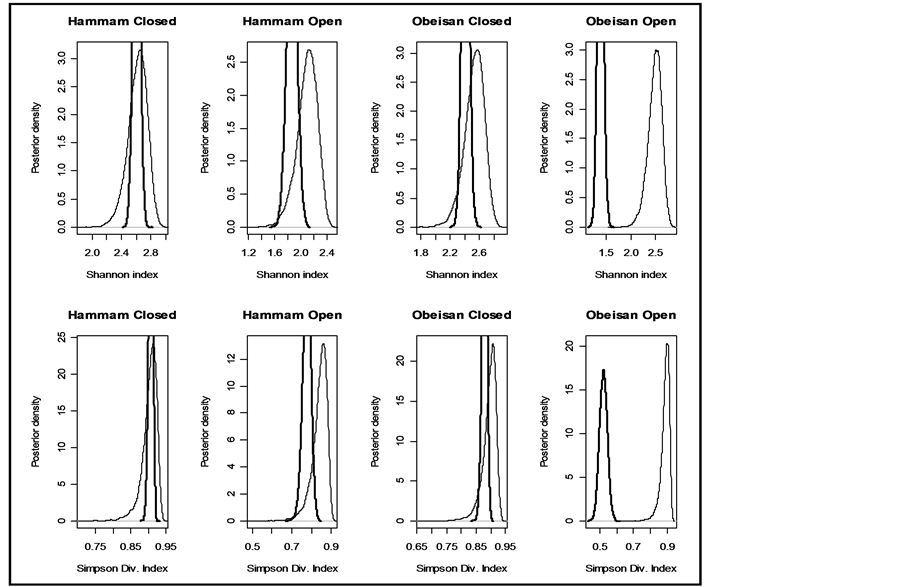
Figure 2. Prior and posterior density of Shannon and Simpson indices for various flattening parameters  (unequal) generated as a random sample from uniform (0.5, k = 1).
(unequal) generated as a random sample from uniform (0.5, k = 1).
Figure 3. Prior and posterior density of Shannon and Simpson indices for various flattening parameters 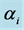 (unequal) generated as a random sample from geometric distribution and restricted in the range (lower = 1, upper = 3, r = 0.2).
(unequal) generated as a random sample from geometric distribution and restricted in the range (lower = 1, upper = 3, r = 0.2).

Continued

Table 3. Estimates and standard errors of diversity indices under frequentist and selected Bayesian models. H: Shannon index. SID: Simpson index of diversity. SE: standard error.
mates (Table 4). The two methods and the two sites show statistically significant differences at 1%, the commonly used level of significance. In most of the cases the p-values were extremely small. However, for the comparison of the two sites under no-grazing (closed), the p-values under the Bayesian approach were lower than those under the frequentist approach. This indicates that use of prior information can result in higher power for the comparisons.
4. Discussion
Bayesian approach is a more general and realistic framework for drawing a statistical inference which utilizes the prior information about the parameters involved. With the availability of computing power, a posteriori distributions of parameters of interest can be obtained in general practice even when involving large number of nuisance parameters. This study, examined the a posteriori distributions of two measures of diversity commonly used in practice. Choice of the prior is an issue that would normally be subjective. However, if the a priori distribution and the a posteriori distribution overlap with high probability on axis of indices then it would be a desirable feature just like a conjugate prior is desirable one in practice. If the probability of their overlap is very low then this indicates that our assumed prior is drifting too much away from the observed reality. The sets of priors used in this study for proportion of species as parameters of the Dirichlet distribution covered a wide range of distribution of diversity indices. The a priori distribution of resulting diversity measures provided a reasonable envelope for their a posteriori distributions.
The selection of the best prior favoured those for which the resulting posterior distribution is close to normality. Since the indices are sums of random variables, their asymptotic distribution could be approximated by normal distribution. One way to examine an effective closeness to normal distribution is in terms of skewness and kurtosis, therefore, a combined index of skewness and kurtosis, as their sum of squares, was introduced. Other ways or methods of creating indices may be worthwhile.
Further, the diversity measures are based on the fact that the number of species was fixed and equal to the same as that which has been observed. There are methods which estimate the number of species using the sample data on the abundances of observed species [30] [31] . Therefore, it would be more realistic to allow for random distribution of not only the proportion or abundance of a given species, but also of the number of species in a given geographical region during a given period of time.
5. Conclusion
A number of priors for the proportion of species were used in obtaining the Bayesian estimates and confidence interval of the two diversity indices. The Bayesian estimates of the diversity were larger, with smaller standard errors, compared to the estimates based on the frequentist approach which ignores any prior information. Significant differences were observed between the diversities of the two sites under each system of grazing management, and also between the two grazing managements at each site. At least in two comparisons, the Bayesian approach resulted in lower p-values. It is recommended that the use of Bayesian approach should be exploited in the estimation of diversity.
Acknowledgements
Authors thank Drs. Mounir Louhaichi and Abdallah Bari, ICARDA for their helpful suggestions on an earlier

Table 4. P-values for comparing the grazing methods and sites for the diversity. H: Shannon index. SID: Simpson index of diversity.
version of the manuscript.
NOTES
*Corresponding author.