IV-VI semiconductors such as Pb1−xSnxSe offer high sensitivity similar to MCT [2]. Until the end of the 1970s, both materials were intensively developed with comparable effort for mid-IR detector applications. MCT became predominantly the material of choice mainly because the permittivity of IV-VI materials is lower than that of MCT, which leads to slow RC response time. At that time, the concerns pertaining to the single-element detector were legitimate. However, this argument does not apply to staring imaging systems that contain a large number of sensors. The large dielectric constant, which is more than 10 times that of MCT, becomes advantageous because coulomb scattering by ionized impurities is strongly suppressed. Consequently, the electric field caused by such defects is shielded within a very short distance. Therefore, IV-VI Pb-salt materials are much more tolerant to defects in comparison to MCT. Due to this effect, Pb-salt materials could have approximately one order of magnitude higher performance than MCT for the same dislocation density [3].
It has been demonstrated that high quality IV-VI semiconductors can be grown on Si substrate. The mismatch of the thermal expansion coefficient was well addressed by a thin CaF2 buffer layer. Dislocation gliding on (111)oriented substrate reduces the threading dislocation density caused by lattice and thermal expansion mismatch [4]. Recently, we have developed a growth method for IV-IV materials on Si substrate that reduces the etch pit density down to 105 cm−2 [5]. These advantages make IVVI materials promising candidates for large-format long wave infrared FPA [6].
In this paper, we present a theoretical investigation for IV-VI Pb1−xSnxSe in the long wavelength spectral range (8 - 11 μm). The influences of different generation-recombination mechanisms to the carrier lifetime are discussed. The resistant-area product (R0A) is divided into three parts for the discussion: diffusion, recombination in junction area, and tunneling. The optimized doping concentration and layer thickness are calculated. The optimized detectivity is over 1012 cm Hz1/2/W.
2. Theory
2.1. Carrier Lifetime
The carrier generation-recombination mechanisms in detector devices are distinguished as band to band Auger’s, radiative and Shockley-Read-Hall’s (SRH) generationrecombination mechanisms. Among them, SRH’s mechanism is determined by the material quality. Auger’s and radiative mechanisms are determined by energy band structures. Therefore, those two are fundamentally limiting factors for the overall generation-recombination processes. In this paper, we consider only Auger’s and radiative mechanisms to exam the PbSnSe material system. More realistic simulation can be performed by considering SRH’s mechanism for a given material quality.
For the radiative process, in case of the Boltzmann statistics, the carrier lifetime is determined by [7]:
 where
where
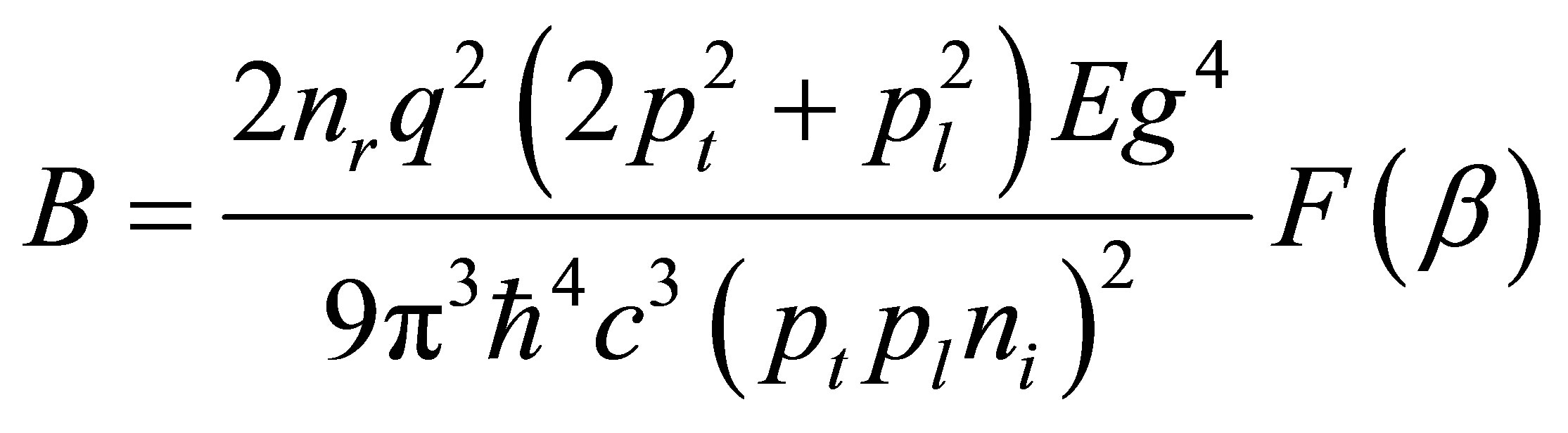 NA is the acceptor concentration which is assumed to be equal to the major carrier concentration in p-type layer, and ni is the intrinsic carrier concentration. The function F(β) is defined as:
NA is the acceptor concentration which is assumed to be equal to the major carrier concentration in p-type layer, and ni is the intrinsic carrier concentration. The function F(β) is defined as:

in which , nr is the refractive index, pt and pl are the momentum matrix elements, Eg is the band gap energy. Based on the experimental data, it is reasonable to assume that the doping concentration
, nr is the refractive index, pt and pl are the momentum matrix elements, Eg is the band gap energy. Based on the experimental data, it is reasonable to assume that the doping concentration , consequently, the corresponding carrier lifetime leads to
, consequently, the corresponding carrier lifetime leads to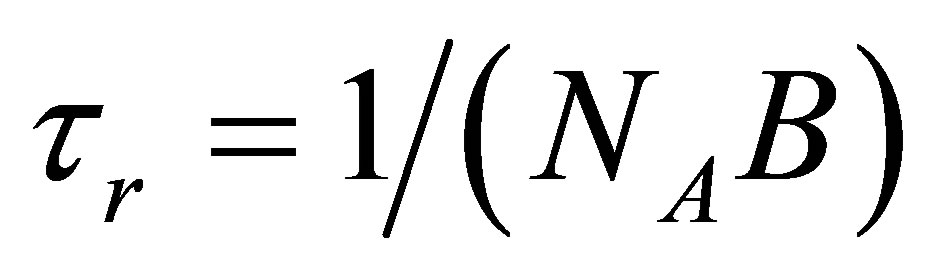 . For the carrier lifetime depending on Auger’s process, the relationship is given by
. For the carrier lifetime depending on Auger’s process, the relationship is given by
 [8]. In the case of
[8]. In the case of , the simplified Auger’s carrier lifetime equation is derived as
, the simplified Auger’s carrier lifetime equation is derived as . The Auger’s recombination coefficient CA is defined as [9]:
. The Auger’s recombination coefficient CA is defined as [9]:
 where
where 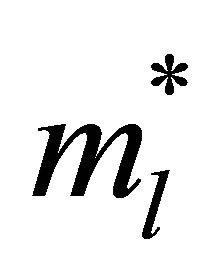 and
and  are the longitudinal and transverse effective masses.
are the longitudinal and transverse effective masses.
2.2. Resistant Area Product (R0A)
For the R0A calculation, we made following assumptions in our model. Firstly, the photodiode in this model is N+-p hetero-structure (the capital letter means the material has larger band gap energy, symbol “+” denotes high doping concentration). The lightly doped p-type layer is sandwiched between the substrate silicon and highly doped, wider band gap N+ layer. The wider band gap N+ layer has smaller absorbance and lower intrinsic carrier concentration. In such a structure, the p-type absorption layer determines both dark current Id and photocurrent Ip of the diode. Secondly, the carrier lifetime is only determined by Auger and radiative mechanisms. Thirdly, we assume the carrier mobility at 77 K is a constant value of 2 × 104 cm2/Vs. Fourthly, the dark current is determined by diffusion-drift, generation-recombinetion and tunneling mechanisms. Finally, we assume that the front side surface is well passivated. Due to the backside illumination mode (light incident through substrate side) and the wider-gap layer, influence of surface recombination on the top surface can be eliminated. The schematic band diagram of epitaxial N+-p Pb1−xSnxSe hetero-junction photodiode is presented in Figure 1.
The R0A product is contributed by diffusion-drift (R0ADD), generation-recombination (R0AGR) and tunneling (R0AT) processes: . The R0A product derived from diffusion current is given by
. The R0A product derived from diffusion current is given by
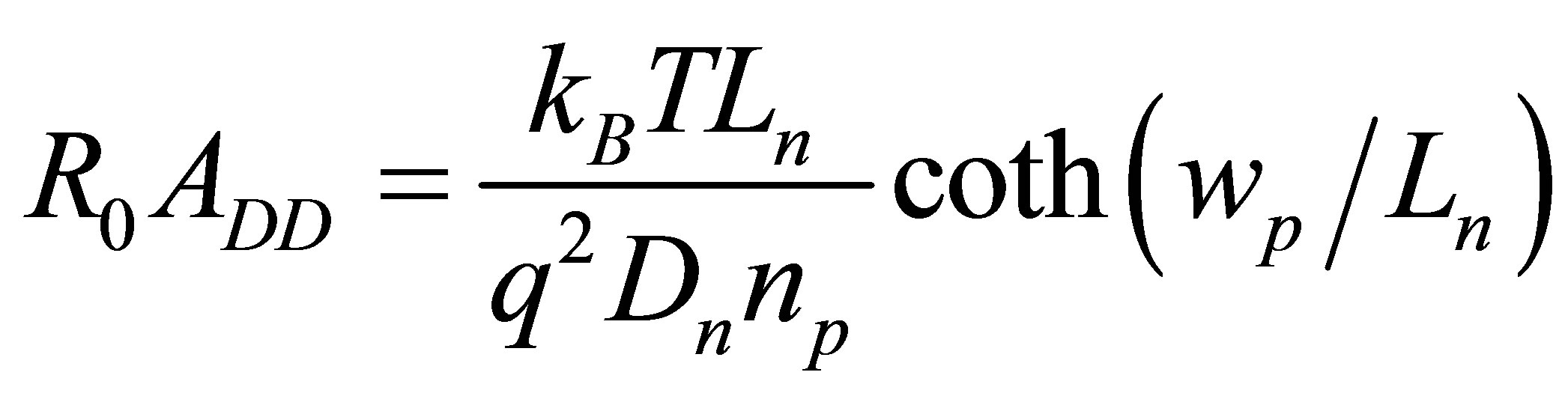 [10]where Dn is the diffusion coefficient, Ln is the electron diffusion length which is equal to
[10]where Dn is the diffusion coefficient, Ln is the electron diffusion length which is equal to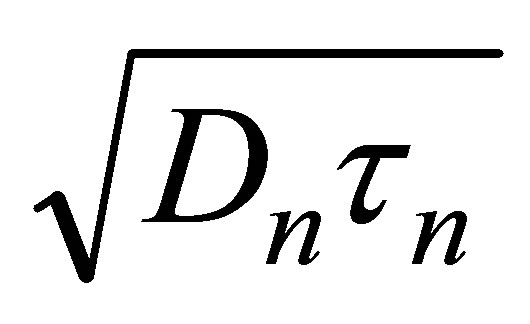 , wp is the thickness of p layer, np is the minority concentration in p layer. The generation-recombination R0AGR determined by the depletion area current is expressed by the equation
, wp is the thickness of p layer, np is the minority concentration in p layer. The generation-recombination R0AGR determined by the depletion area current is expressed by the equation
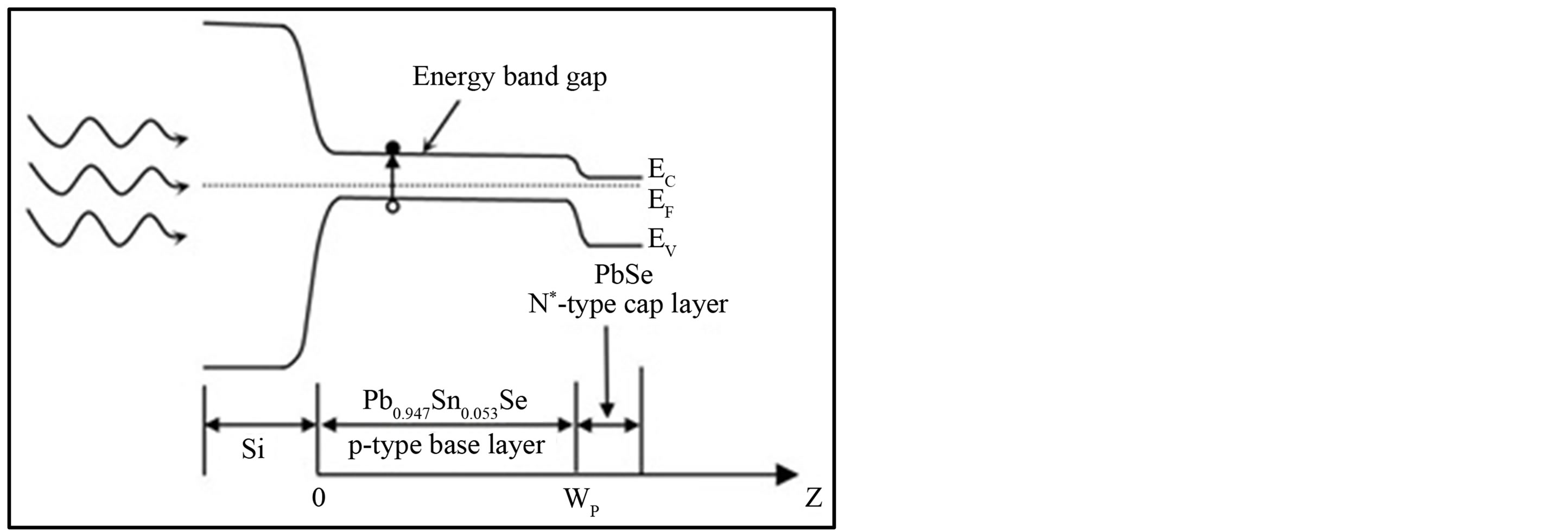
Figure 1. Schematic energy band diagrams of epitaxial N+-p Pb1−xSnxSe hetero-structure.
 [11]where εs is the static dielectric constant. We assume that the lifetime in junction and neutral area is the same. The contribution to R0A by the tunneling mechanism is given by
[11]where εs is the static dielectric constant. We assume that the lifetime in junction and neutral area is the same. The contribution to R0A by the tunneling mechanism is given by
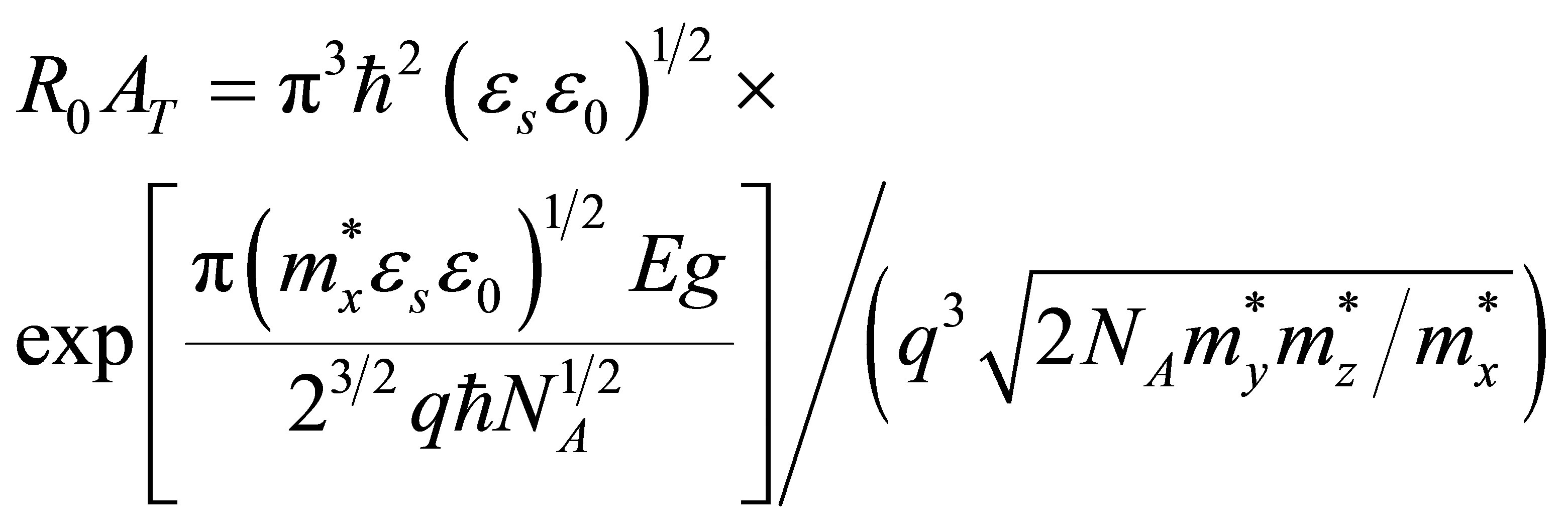 [12]where
[12]where ,
,  , and
, and  are the orientation dependent effective mass components. For IV-VI materials, they are given in Table 1.
are the orientation dependent effective mass components. For IV-VI materials, they are given in Table 1.
2.3. Quantum Efficiency
The reflectivity of radiation is a limiting factor for quantum efficiency. IV-VI group materials have very large dielectric constants. As a result, for the frontside illumination mode, the reflection loss can be more than 50%, for the backside illumination mode, the loss just decreases down to 30% due to the lower dielectric constant of the substrate Si. However, antireflection coating can be used to increase transimission close to unity. In this work, we assume the light incidence is 100% transmission.
In the hetero-junction structure, Rosenfeld etc. used one dimensional model to derive the net quantum efficiency. Its formula is slightly modified in this work and shown as follows [14]:
 where
where
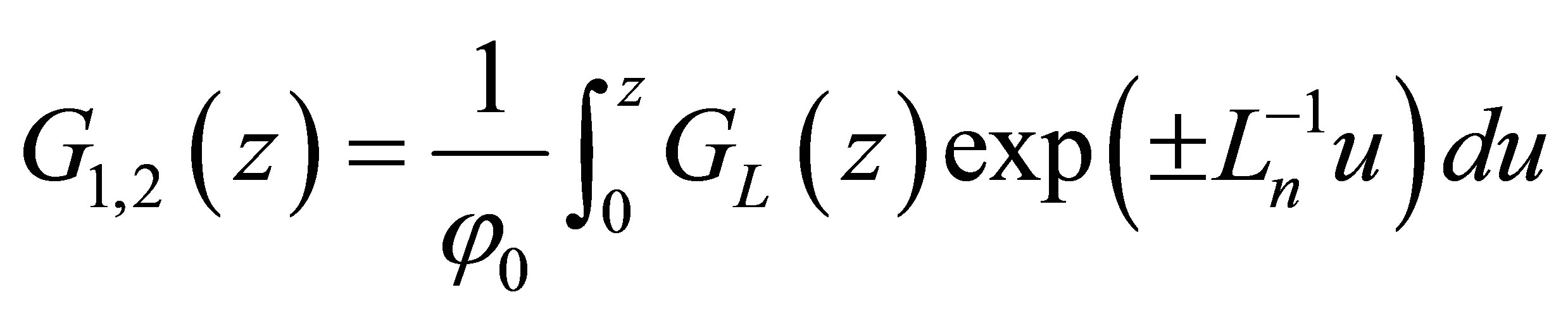 ,
,
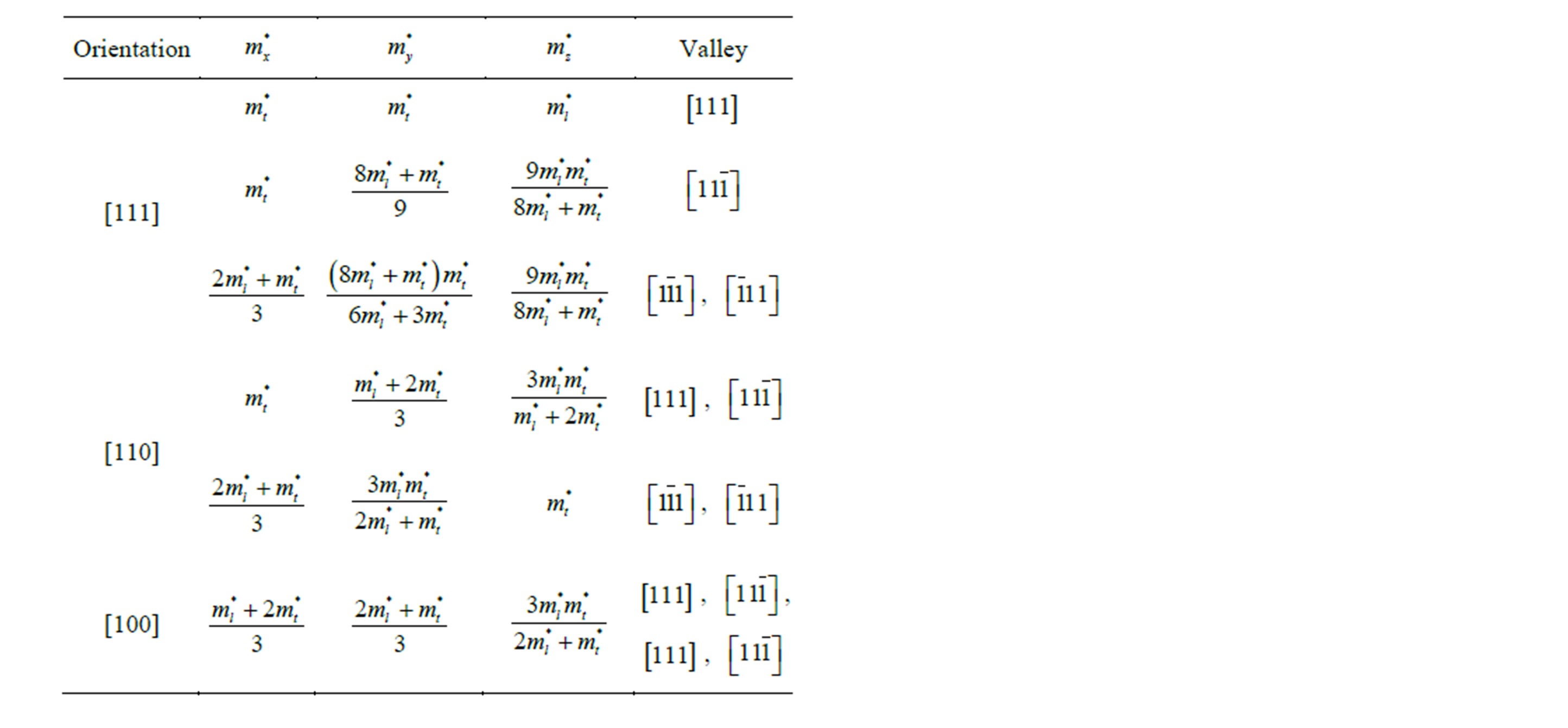
Table 1. Orientation dependent effective mass [13].
where the monochromatic backside illumination generation rate GL(z) is defined as
 in which
in which  is the photon flux at the edge of the absorption layer (z = 0) and
is the photon flux at the edge of the absorption layer (z = 0) and  is the absorption coefficient which is dependent on Sn composition. It is given by the two band model relation
is the absorption coefficient which is dependent on Sn composition. It is given by the two band model relation
 [15]in which ω stands for the angle frequency of the incident light.
[15]in which ω stands for the angle frequency of the incident light.
The quantum efficiency described above is associated with the monochromatic photon flux. However, the detectors are normally exposed to a wide spectral range flux as described by Plank’s radiation law. Consequently, the weighted average of the quantum efficiency can be given by
 where n(λ) is the spectral radiant photon emittance of the target.
where n(λ) is the spectral radiant photon emittance of the target.
2.4. Detectivity
The detectivity is the most important figure of merit for detectors. The Johnson-Nyquist noise dependent detectivity is given by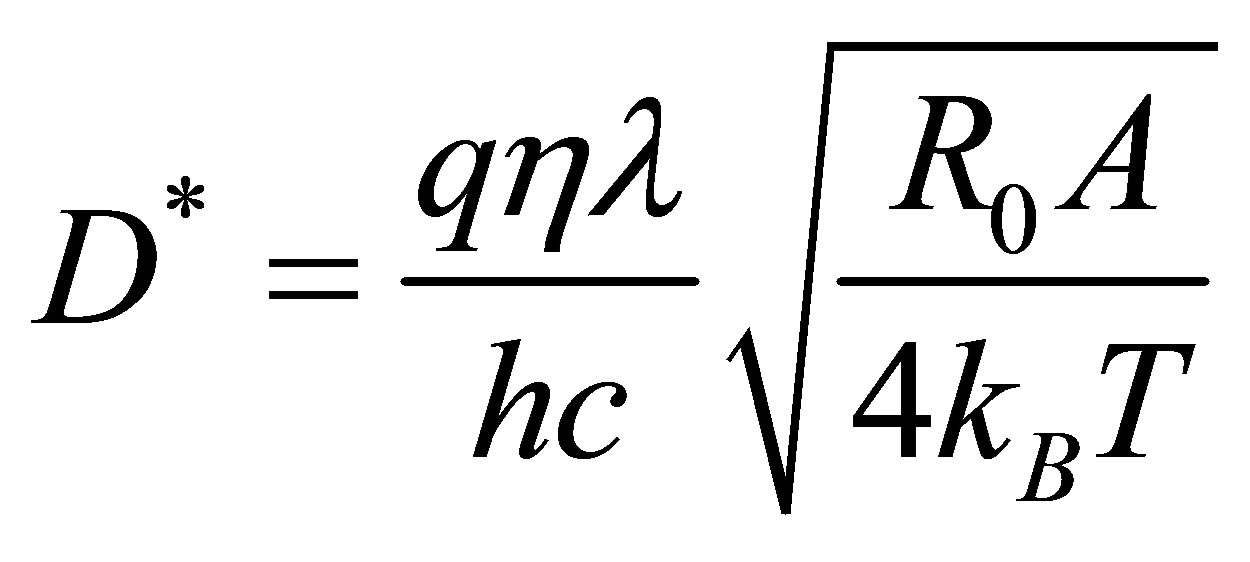 . From this formulait is denoted that D* is associated with both resistant area product R0A and quantum efficiency η. Shot noise dependent detectivity is not discussed in our model.
. From this formulait is denoted that D* is associated with both resistant area product R0A and quantum efficiency η. Shot noise dependent detectivity is not discussed in our model.
3. Results and Discussions
3.1. Optimization of Doping Concentration
The parameters for the simulation are listed in Table 2. As can be seen, all of the parameters except mobility and εs are dependent on Sn composition and the temperature. In terms of this condition, the simulated results should be convincible in Pb1−xSnxSe system. The Sn compositions of 0.053 and 0 are used for p-type Pb0.947Sn0.053Se layer and N+PbSe layer, respectively.
Figure 2 shows Auger’s lifetime (solid dot), radiative lifetime (solid square) and the total lifetime (solid line) with acceptor concentration in p layer of Pb0.947Sn0.053Se. While NA is larger than 1 × 1017 cm−3, Auger’s mechanism dominates the material lifetime. The lifetime is less than 10 ns when the doping concentration is 2 × 1017 cm−3. When NA is lower than 1 × 1017 cm−3, lifetime influenced by the radiative mechanism is increasing more slowly than the Auger’s one. The lifetime is over 100ns when concentration is 3 × 1016 cm−3. This is because Auger’s lifetime is proportional to  and radiative lifetime is proportional to
and radiative lifetime is proportional to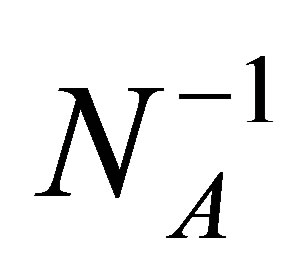 . In all, total lifetime decreases rapidly with the increase of NA.
. In all, total lifetime decreases rapidly with the increase of NA.
Figure 3 shows the R0A for different doping concentrations NA at 77 K. The thickness of p layer is 16 μm. Three mechanisms are taken into consideration. The resistant area product R0A caused by the tunneling process is proportional to exponential , as a result, R0A drops dramatically as NA is over 1 × 1017 cm−3. Overall, R0A decreases with the increase of NA, and the value varies slightly when NA is under 1 × 1017 cm−3.
, as a result, R0A drops dramatically as NA is over 1 × 1017 cm−3. Overall, R0A decreases with the increase of NA, and the value varies slightly when NA is under 1 × 1017 cm−3.
Therefore, both lifetime and R0A increase as the acceptor concentration NA decreases. Since the typical NA for Pn1 − xSnxSe is between 1 × 1016 cm−3 and 1 × 1017 cm−3 at 77 K, we use NA of 3 × 1016 cm−3. The corresponding lifetime is approximately 100 ns. The diffusion length Ln is 36.4 μm. In this case, the diffusion length is twice as long as the absorption thickness. Thus, all carriers generated in this layer will be collected.
3.2. Optimization of the Thickness of Absorption Layer
The quantum efficiency is sensitive to the thickness of the absorption layer. Based on the discussion above, we use a lifetime of 100 ns and NA of 3 × 1016 cm−3, and the energy band gap of 0.115 eV. (Corresponding wavelength is 11 μm). Figure 4 shows the relationship between

Table 2. Physics properties of Pb1−xSnxSe [11], [16], [17].
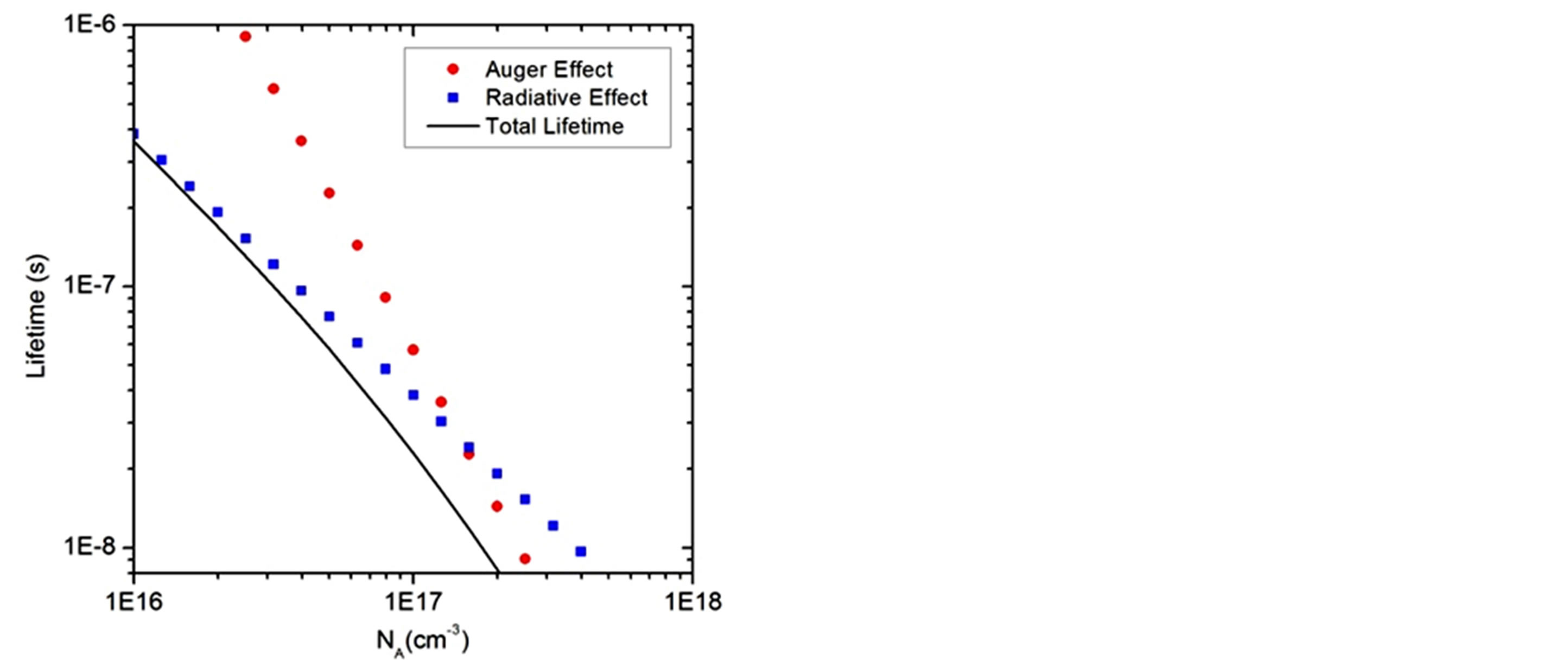
Figure 2. Lifetime versus acceptor concentrations at 77 K.

Figure 3. The resistant area product R0A versus acceptor concentration NA at 77 K.
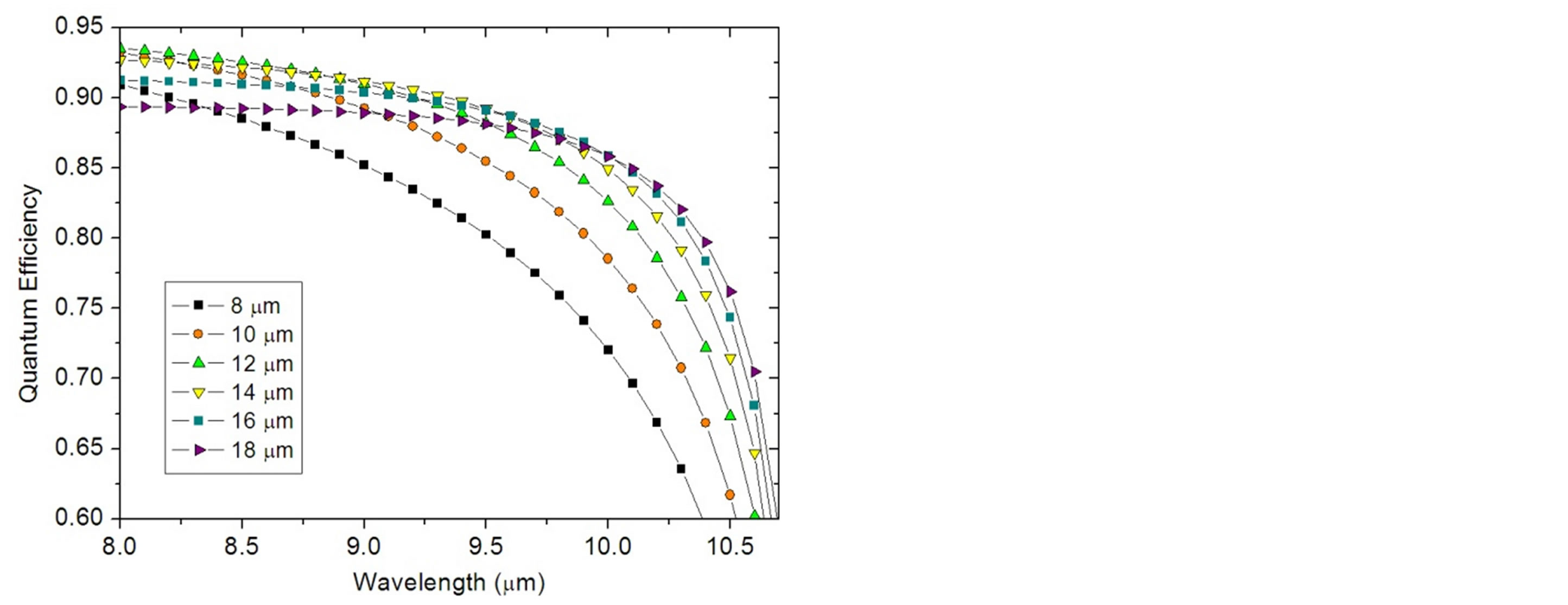
Figure 4. Quantum efficiency with different thicknesses in long wavelength range at 77 K.
quantum efficiency and absorption thickness in the long wavelength spectral range 8 to 11 μm. In this figure, quantum efficiencies decrease as incident wavelength increases. As can been seen, 12 μm thickness gives the highest value of about 95% at 8 μm.
We apply weighted average of quantum efficiency to define the optimal thickness with the best performance. The background radiation temperature is at 300 K. The simulation result is given in Figure 5. It denotes average quantum efficiency rising rapidly from 8 µm to 14 µm. And around 16 µm thickness, the quantum efficiency value reaches the peak.
3.3. Detectivity
With the calculated quantum efficiency and lifetime value. Figure 6 shows the simulated D* for different Pb1−xSnxSe p-type layer thickness at 77 K. For thickness between 10 to 18 µm, D* value is over 1012 cm Hz1/2/W.
To our knowledge, the highest reported theoretical D* for HgCdTe N+-p photodiode in long wavelength spectral range (8 - 11 μm) is 9 × 1010 cm Hz1/2/W at 77 K [18]. We would like to point out that their simulation included the surface recombination process with a surface recombination velocity (SRV) of 104 cm/s. When we consider surface recombination using the same SRV the R0A changed slightly from 41 to 40 ohm·cm2. Since quantum efficiency depends weakly on SRV our simulated D* value remains almost the same. This D* value of Pb1−xSnxSe is more than one order of magnitude larger than the simulated D* of MCT’s in reference [18].
4. Conclusion
The one dimensional Pb1−xSnxSe photovoltaic diode simulation model has been discussed in this work. We calculated the lifetime, R0A, absorption, quantum efficiency and detectivity for structure N+-p heterojunction on Si
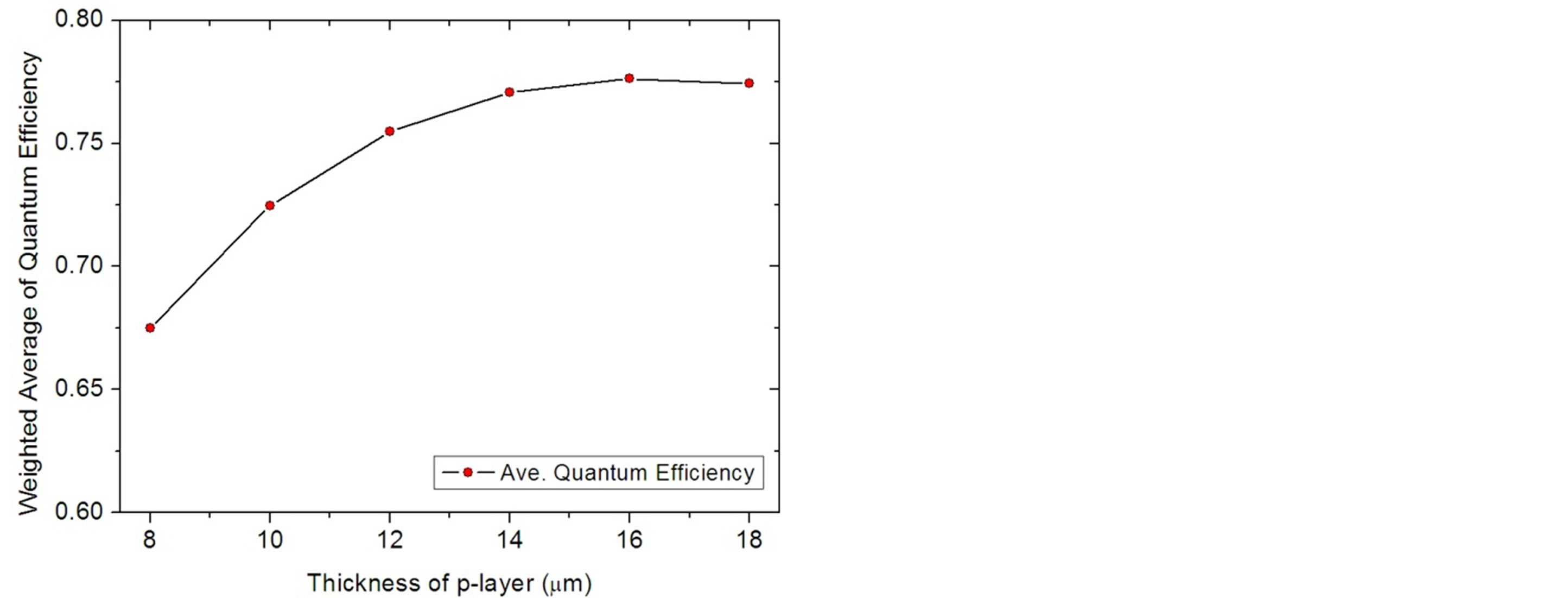
Figure 5. The weighted average of quantum efficiency versus the thickness of player at 77 K.

Figure 6. Detectivity D* versus absorption thickness in 8 - 11 µm spectral range at 77K.
substrate. The optimized D* value obtained is over 1012 cm Hz1/2/W. This result indicates a great potential for PbSnSe detector with superior detectivity to be fabricated.
Acknowledgements
We acknowledge financial supports from the DoD AFOSR under Grant No. FA9550-12-1-0451, DoD ARO Grant No. W911NF-07-1-0587, and Oklahoma OCAST program under Grant No. AR112-18 and No. AR132-003.