Numerical Solutions for the Time-Dependent Emden-Fowler-Type Equations by B-Spline Method ()
1. Introduction
In recent years, a lot of attentions have been devoted to the study of B-spline method to investigate various scientific models. The efficiency of the method has been formally proved by many researchers [1] -[7] .
Spline functions have some attractive properties. Due to the being piecewise polynomial, they can be integrated and differentiated easily. Since they have compact support, numerical methods in which spline functions are used as a basis function lead to matrix systems including band matrices. Such systems have solution algorithms with low computational cost.
In this paper, we employ the B-spline method to solve the time dependent partial differential equations. For clarity, the method is presented for the heat equation
 (1)
(1)
subject to the boundary conditions
 (2)
(2)
and the initial condition
 (3)
(3)
Some forms of the above equations model several phenomena in mathematical physics and astrophysics such as the diffusion of heat perpendicular to the surface of parallel planes, theory of stellar structure, the thermal behavior of a spherical cloud of gas, isothermal gas sphere and theory of thermionic currents [8] -[10] .
The solution of the time-dependent Emden-Fowler equation as well as a variety of linear and nonlinear singular IVPs in quantum mechanics and astrophysics is numerically challenging because of singularity behavior at the origin. The singularity behavior that occurs at the point  is the main difficulty in the analysis of Equations (1)-(3).
is the main difficulty in the analysis of Equations (1)-(3).
The approximate analytical solutions to the Lane-Emden equations were presented by Shawagfeh [11] and Wazwaz [12] -[14] using the Adomian decomposition method (ADM). Very recently, Chowdhury and Hashim [15] applied the homotopy-perturbation method (HPM) and the variational iteration method (VIM) [16] to obtain approximate analytical solutions of the time-dependent Emden-Fowler-type equations.
The paper is organized as follows. In Section 2, we review some basic facts about the B-spline that are necessary for the formulation of the discrete linear and nonlinear system. In Section 3, the error analysis of the method is described. In Section 4, we formulate our B-spline collocation method to the solution of (1)-(3). In Section 5, numerical experiments are tested to demonstrate the viability of the proposed method.
2. Some Properties of B-Spline
B-splines are mathematically more sophisticated than other types of splines, so we start with a gentle introduction. We first use basic assumptions to derive the expressions for the cubic uniform B-splines directly and without mentioning knots. We then show how to extend the derivations to uniform B-splines of any order. Following this, we discuss a different, recursive formulation of the weight functions of the uniform B-splines.
The third-degree B-spline is used to construct numerical solutions to a given problem (1). A detailed description of third-degree B-spline functions can be found in [13] [17] . The third-degree B-splines are defined as
 (4)
(4)
 (5)
(5)
We can simply check that each of the function  is twice continuously differentiable on the entire real line. Also,
is twice continuously differentiable on the entire real line. Also,
 (6)
(6)
Similarly, we can show that:
 (7)
(7)
and
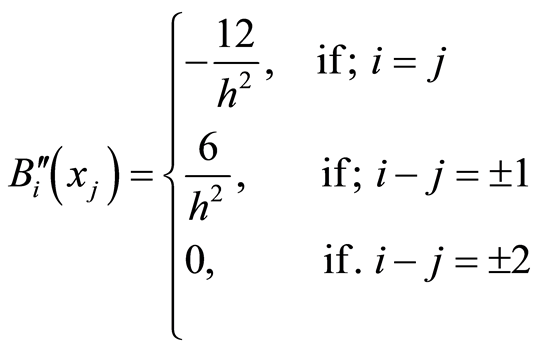 (8)
(8)
3. Error Analysis
3.1. Governing Equation
Since  is singular point of Equation (1), we first modify Equation (1) at
is singular point of Equation (1), we first modify Equation (1) at  By L’Hospital rule, the boundary value problem (1) is transform into
By L’Hospital rule, the boundary value problem (1) is transform into
 (9)
(9)
where

Let , we consider the linear non-homogeneous Emden-Fowler differential Equation (9), difference schemes for this problem considered as following:
, we consider the linear non-homogeneous Emden-Fowler differential Equation (9), difference schemes for this problem considered as following:
 (10)
(10)
or
 (11)
(11)
Suppose  is the cubic B-spline interpolating
is the cubic B-spline interpolating  at the
at the 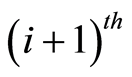 time level then
time level then
 (12)
(12)
Theorem 3.1. Let the collocation approximation  to the solution
to the solution  of the boundary value problem (1) is (12) then the following relation is hold
of the boundary value problem (1) is (12) then the following relation is hold
 (13)
(13)
3.2. Truncation Error of Time Dependent Emden-Fowler Equation
Theorem 3.2. By using the combination of the finite difference approximation and cubic B-spline method, the truncation error is .
.
Proof: Consider the Equation (10) when apply finite difference

apply taylor expansion for L.H.S


if

we can calculate the truncation error which is defined as  as:
as:

4. B-Spline Solutions for Time-Dependent Emden-Fowler
In this section, we shall introduce a reliable algorithm based on B-spline method to handle singular initial value problems (IVPs) in a realistic and efficient way considering Emden Fowler equation as a model problem.
4.1. Linear Time-Dependent Emden-Fowler
Let
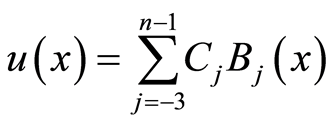 (14)
(14)
be an approximate solution of Equation (1), where  are unknown real coefficients and
are unknown real coefficients and  are thirddegree B-spline functions. Let
are thirddegree B-spline functions. Let  be
be  grid points in the interval
grid points in the interval  so that
so that

We can deduce the following
 (15)
(15)
Theorem 4.1. If the assumed approximate solution of the problem (10) is (14), then the discrete collocation system for the determination of the unknown coefficients  is given by
is given by
 (16)
(16)
Proof: If we replace each term of (10) with its corresponding approximation given by (14) and (15) and substituting  and applying the collocation to it.
and applying the collocation to it.
The boundary conditions (3) can be written as
 (17)
(17)
Then use them with the system of Equation (16), which can be written in the matrix form
 (18)
(18)
where

Also the matrix  can be written as
can be written as

where

It is easily seen that the matrix  is strictly diagonally dominant and hence nonsingular. Now we have a linear system of
is strictly diagonally dominant and hence nonsingular. Now we have a linear system of  equations for the
equations for the  unknown coefficients, namely,
unknown coefficients, namely, . We can obtain the coefficient of the approximate solution by solving this linear system by Q-R method.
. We can obtain the coefficient of the approximate solution by solving this linear system by Q-R method.
4.2. Non-Linear Time-Dependent Emden-Fowler
Let , we consider the nonlinear non-homogeneous Emden-Fowler differential equation
, we consider the nonlinear non-homogeneous Emden-Fowler differential equation
 (19)
(19)
We can use finite difference method
 (20)
(20)
Theorem 4.2. If the assumed approximate solution of the problem (20) is (14), then the discrete collocation system for the determination of the unknown coefficients is given by
 (21)
(21)
Then the boundary condition (17) with the system of Equation (21). Now we have a nonlinear system of  equations in the
equations in the  unknown coefficients. We can obtain the coefficients of the approximate solution by solving this nonlinear system by Newton’s method.
unknown coefficients. We can obtain the coefficients of the approximate solution by solving this nonlinear system by Newton’s method.
5. Examples and Comparisons
In this section, we will present three of our numerical results of time dependent problems using the method outlined in the previous section. The performance of the B-spline method is measured by the maximum absolute error 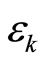 which is defined as
which is defined as

Example 1: [18] Consider the problem

subject to boundary conditions

and the initial condition

whose exact solution is

The maximum absolute errors at different  and different time
and different time  with
with  is given in Table 1.
is given in Table 1.
Example 2: [18] Consider the linear problem

subject to boundary conditions

and the initial condition

whose exact solution is

Table 1. Maximum absolute errors for Example 1.

The maximum absolute errors at different  and different time
and different time  with
with  is given in Table 2.
is given in Table 2.
Example 3: [18] Now we turn to a singular nonlinear problem

subject to boundary conditions

and the initial condition

whose exact solution is

The maximum absolute errors at different  and different time
and different time  with
with  is given in Table 3.
is given in Table 3.
6. Conclusions
We have presented a B-spline collocation method for the solution of time-dependent Emden Fowler type Equations (1)-(3). This method produces a spline function which is useful to obtain the solution at any point of the interval, whereas the finite difference method gives the solution only at selected nodal points. The numerical results given in tables show that the present method approximates the exact solution very well.
This present analysis exhibits the reliable applicability of B-spline method to solve linear and nonlinear problems with singular feature. In this work, we demonstrate that this method can be well suited to attain solution to the type of examined equations, linear and nonlinear as well. The difficulty in this type of equations

Table 2. Maximum absolute errors for Example 2.

Table 3. Maximum absolute errors for Example 3.
due to the existence of singular point at  is overcome here. Finally, we conclude that the B-spline method is a promising tool for both linear and nonlinear singular time-dependent Emden-Fowler-type equations.
is overcome here. Finally, we conclude that the B-spline method is a promising tool for both linear and nonlinear singular time-dependent Emden-Fowler-type equations.