Theoretical Modeling and Experimental Analysis of Drying Process in Electromagnetic Field ()
1. Introduction Main building components of all fruit and vegetables are foreboded to be water. Per contra, microorganisms absolutely need the water for metabolisms. The life of microorganisms causes deterioration of fruit and vegetables. For this reason, the amount of water in their composition is required to reduce or totally eliminate for prolonged storage of fruit and vegetables. Prolonged protection method by means of reduction of the water contained in foods is one of the oldest methods practiced by people in food preservation . In drying of food production, dehydration process with the aid of solar energy or the heat obtained from other sources is under way. In the second method, impending “convection drying”, “contact drying” and “radiation drying” according to the methods to move heat required in order to remove the water from the product dried, three drying methods are mainly used - . In addition, two speared “dielectric drying” and “discontinuous drying” methods are used in the construction and textile industry. The heat in dielectric drying, “dipoles” of the dielectric materials in high-frequency electric field composed as a result of friction obtained the displacement. The heat in discontinuous vacuum drying is obtained by bringing light of hidden energy in matter. In 1970-1980 of the last century, tobacco drying in magnetic field has been tried . In this method, eddy currents occur depending on the frequency of the magnetic field and these currents cause the formation of heat. That should be taken into consideration throughout drying fruits and vegetables varying both color and chemical structure - . Optimal drying conditions in order to reduce to the lowest level of these changes should be selected. The accelerating method of classical drying systems for the creation of optimal drying conditions can be more important. In practice for this purpose, sulfur dioxide gas (SO2), the implementation of electrical and magnetic field and blushing of fruit and vegetables , - are used for management. Magnetic and electric fields are widely used in recent years in order to accelerate the drying process of fruit, vegetables, and food materials. Under the influence of the magnetic field in drying process, events arise such as the increase of the temperature permeability of medium, temperature increasing due to the formation of electric field throughout closed-loop in the liquid medium and fragmentation of heterogeneous environments because of diversity of magnetic permeability of different phases. The effect of the electrical field in dried environment leads to the emergence of many physic-chemical phenomena. Because of different characteristics of phases dried in electrical operation, the environment of heterogeneous is performing fragmentation. In electrophoresis processes, heating of the material is performed by creating a current in the electrical field with the effect of marked electrical loads in hard and liquid phases. In addition, temperature in this medium due to electrical current passing in dried environment can be created.
In literature, study results and information belonging to drying materials in the electric field , , magnetic field , and electromagnetic field , are presented. In this study, the results of experiments under the influence of constant magnetic field , high-frequency and high-voltage electric fields , , high-frequency (microwave) fields , , and the results from the use of their different theoretical methods are presented. In other study , determination of the effective diffusion coefficient of humidity considering the effect of low-frequency magnetic field and deformation of dried material is determined, such as the solution of the inverse problem. In reference , drying porous-capillary layer of glazing spheres is taken into consideration, and the effect of drying kinetics parameters of the particles moistness and electromagnetic fields are experimentally examined. As a result of investigations, calculation of humidity transport current in porous surroundings, as the sum of resultant moving current induced by diffusion and magnetic field is proposed. All components of the theory and practice of these events including many physical and chemical changes are not possible after enough examination.
In this study, accelerating the drying processes’ events effects of electromagnetic wave (EMW) of materials having different physical and chemical properties are investigated theoretically and experimentally. Experimental investigations without EMW effect and EMW effect in drying system designed especially for this purpose have been carried. EMWs having a certain frequency have been identified as accelerating the effective drying process. The creation of the theoretical model for drying effect of EMW has been attempted. Two-port circuit which is widely used and examined in detail in electric circuit theory has offered a suggestion for the determination of the basic diffusion coefficients that assess the mass transfer events in drying process. Theoretical and experimental results which have been obtained are identified as a well adaptation.
2. Problem Formulation and Mathematical Model In the analysis of the electromagnetic field effect problems in mass transfer events occurred porous environment or drying process in material, provided that the fallowing conditions are assumed.
• The solid material sample which is examined composed of porous layer shaped a rectangular or circular of finite dimension in the thickness 2δ.
• Opposed surface of the porous material has heat and mass transfer by the effect of air flow and electromagnetic field. Velocity of the air which is blown off constant during the drying process and air flow is speared over homogeneously on the surface of the material.
• The effect of the electromagnetic field generated with electrical (E) and magnetic (B) fields affecting in the direction perpendicular to each other. Electromagnetic field is an alternative field.
• Heat and mass transfer formed are a one-dimensional process.
• Chemical reaction does not occur in material during the drying and the chemical structure of the material does not change. Material has a homogeneous structure.
Take into consideration these circumstances, surface of the sheet of material which dimensions L and b, thickness 2δ is exposed to a laminar air flow in the T∞ = const initial temperature (Figure 1). M0 is initial moisture concentration. Material is composed of capillary porous and this material undergoes changes in volume during drying. Due to the air flow that direction of y-axis, maximum transmission of air temperature will be in this direction. Instantly t = 0, electromagnetic field which have been created from electric (E) and magnetic (B) fields towards perpendicular to each other to layer has shown an impact. This field generates an electromagnetic wave (EMW) in the direction of z-axis. This EMW, in layer of material which is examined will give rise to additional heat source. Temperature created by the source will spread as a homogeneous in layer. According to the amount of moisture contained in the dried material changed during drying, the resistance exhibited to EMW of this medium or wave impedance that determines the spread in this environment of EMW will change. Heat and mass transfer are considered in mathematical model of the drying process. This process is performed by the following approach.
In general, all of the parameters that affect the process of drying of porous materials have a non-linear change according to time and temperature. Therefore a general theoretical model creation of these processes is considerably difficult. In the literature, different empirical expressions and experimental curves are presented for the parameters that determine these processes. These expressions obtained considering the local conditions are not sufficient to create a general approach to the solution of the problem. On the other hand considering some of the conditions and assumptions, simple relationships between these parameters can be obtained.
Cross-section of layer of drying material is demonstrated in Figure 2. As can be seen in Figure 2, material layer in drying process has contracted, deformed all surfaces and dimension of the layer has decreased. In other words, the maximum deformation of material layer comes into the existence in the z-axis. Considering the assumption above, the mass change in the z-axis (mass conservation) can be written as following according to the second law of Fick’s equation.
 (1)
(1)
Here Delm refers to diffusion consisting by the effect of electromagnetic field and gets the name of electromagnetic diffusion coefficient; U is shrinkage velocity of material surface. In general, heat diffusion coefficient of Deff and Delm have the different structure because of the dissimilar physical process of EMW events. For this reason the analytic solution of equation (1) is difficult or impossible. Thus solution of this equation can be obtained by either numerical methods or a difficult mathematical approach. In this study, equation (1) is shown as follows convective, diffusion and superposition of diffusion process comprising the impact of EMW.
 (2)
(2)
 (3)
(3)
In this place, M' resulting from convective diffusion, M'' emerging a result of diffusion consisting the effect of EMW refer to the amount of mass transfer. In this case, the amount of exact mass transfer;
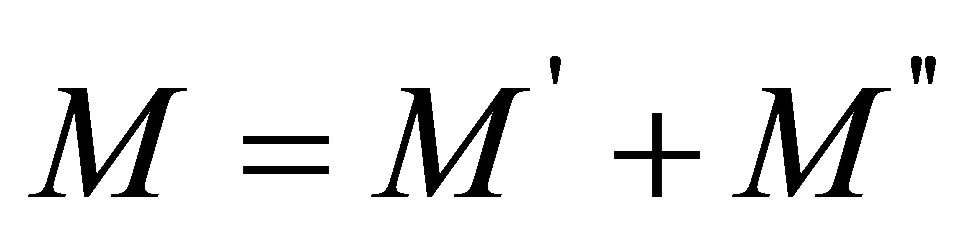 (4)
(4)
Determine by the expression.
In general, equations of heat and mass transfer are presented numerous solutions and methods in the literature

Figure 1. The general scheme of the dried sample material.

Figure 2. The geometry of dried material sample.
- , , - . Selecting the different coefficients, determination and the implementation of approximately solution methods in these solutions has been made. The results obtained consist of complex mathematical expression in many cases and are not apply handy in the practice of engineering. However taking into consideration the similarity of process flow, heat and mass transfer equations can be easily modeled with the different physical processes.
Equations expressed in many process similar to equation (2) and equation (3) used in electrical circuits and systems, and the electromagnetic theory. For example, processes expressed in similar to equation (2) and equation (3) can be modeled with the theory of two-port widely used in electrical circuit theory. The main advantages of this model are a comprehensive study of the theory of two-port in electrical circuit theory and simple analytical connections in between the parameters of the two-port.
2.1. Modeling of diffusion equations with electric circuit theory Principle diagram of simple two-port system is shown in Figure 3. Events occurring in a system according to the theory of the two-port are determined corresponding relation between input (two-ports) and output (current-voltage) parameters of this system. Flow type of processes in the two-port are insignificant and the characteristic of the system is determined with the relationship between them and its input and output parameters. In generally, drying process of materials can be modeled the fallowing approach according to two-port electrical circuit theory.
Material which has dried and having a certain geometry and volume is assumed that a two-door. Input and output parameters that determine the drying process of these two-doors are as follow;
ρ—Density together with water mass of material (kg/m3);
ρ0—Density of liquid mass resulting volume of material by the effect of diffusion (kg/m3);
Q—Heat current (y) entering volume of material;
Q0—Heat current (y) emerging with the vapor of liquid from the volume of material.
In these conditions, the following equations can be written according to the theory of a two-port in accordance with the Figure 3.

Figure 3. Diagram of a simple two-port circuit.
 (5)
(5)
 (6)
(6)
Here, A11, A12, A21, A22 are the coefficient of the two-ports. These coefficients are dependent on geometry and dimension, internal structure, physical and chemical properties of the two-door or the volume of material. According to the schema of equivalent two-pole shown in Figure 3, A11, A12, A21, A22 coefficients are determined as follows.
 (6)
(6)
 (7)
(7)
When π theorem applied to take into consideration the second equation in equation (5) and equation (6) and after making some mathematical operations, rate of moisture concentration can be determined as follow on convective diffusion in drying process,
 (8)
(8)
Here, k1 and k2 are constant of the system and are determined according to equation (7). In this equation, T, T∞, t, t∞ represent to expression temperature, the blown air temperature, time, reference time respectively and Bi is Biot number.
 (9)
(9)
Dmol is molecular diffusion coefficient in equation (9) and according to Einstein formula is generally written as follows;
 (10)
(10)
Here, m—mass of liquid vapor separated as a result of diffusion, k—Boltzmann constant, µd—move capability. Mass transfer coefficient (hm) can be determined from equation (13) as Equation (9),
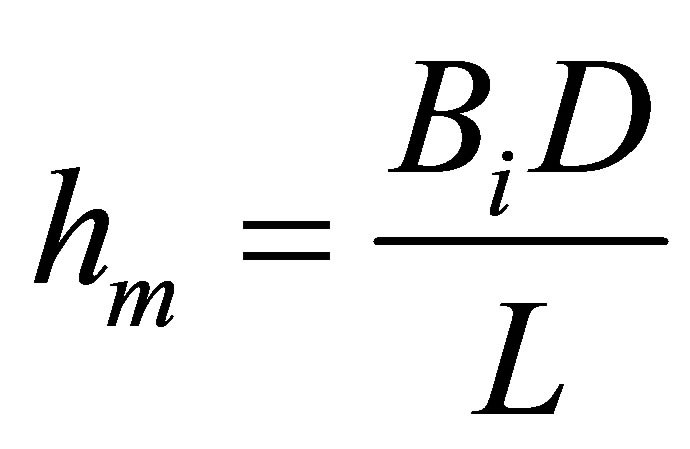 (11)
(11)
As seen in the above expression, Biot number (Bi) varies depending porous material, time and temperature. Whereas porous of material dried is not easy to determine both theoretically and experimentally. Thus, exchange porous of material in drying process can be taking into account. Due to the possibility of measuring time and temperature during the experiment,
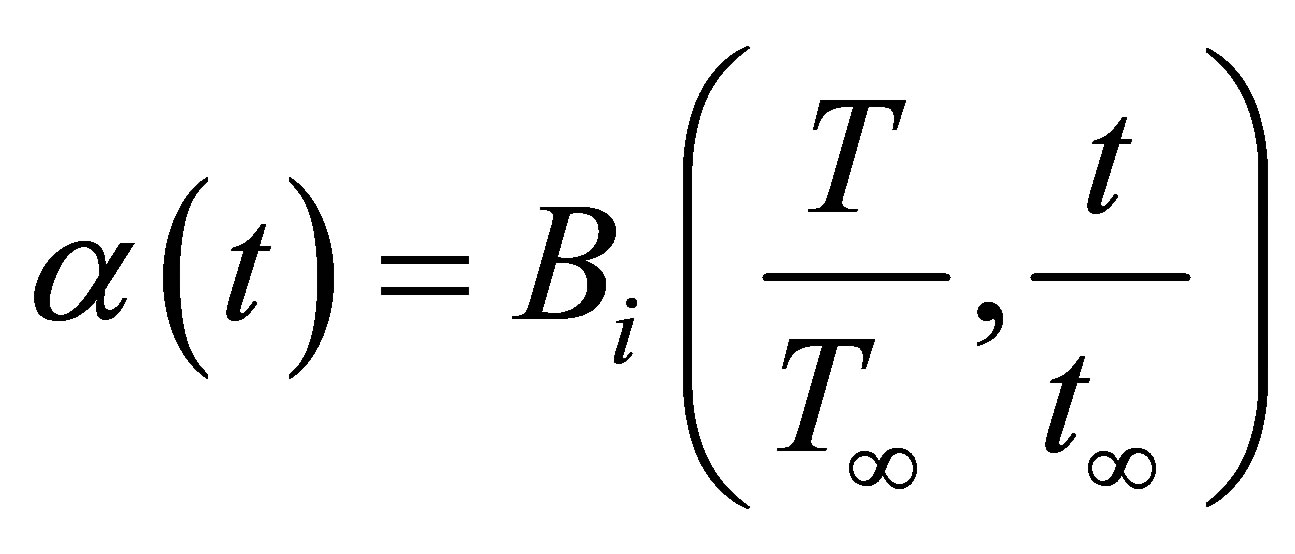 (12)
(12)
Making the transformation, equation (8) can be written the simplest possible manner.
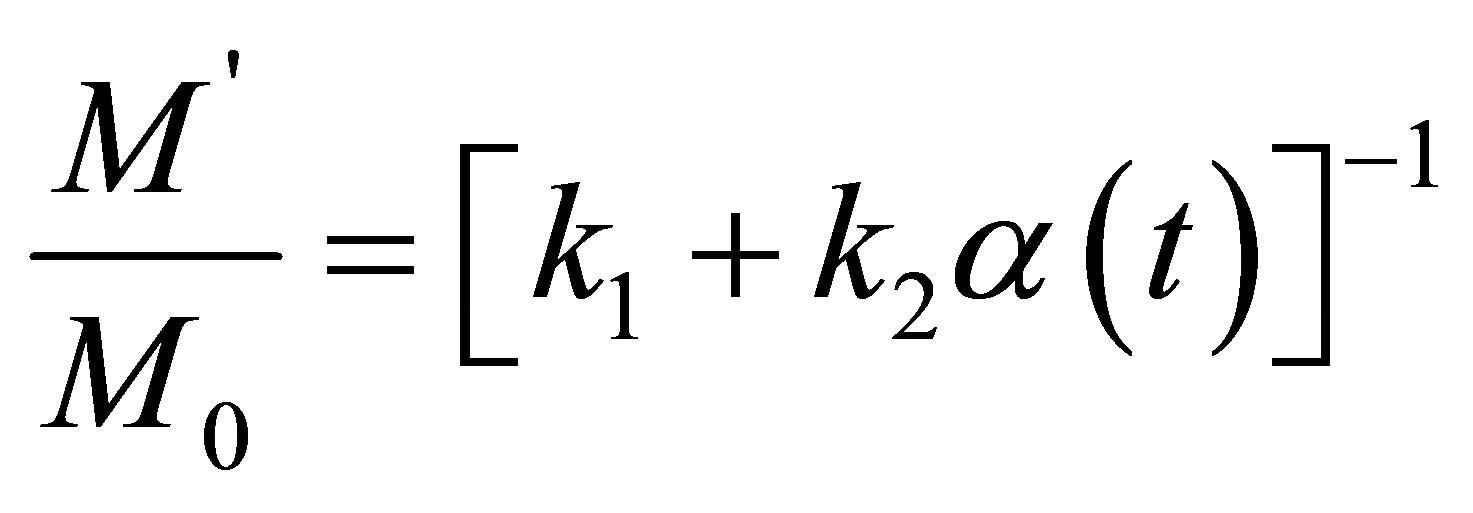 (13)
(13)
Therefore, taking advantage of a two-port theory (equation (5) and equation (6)), moisture proportion of convection drying process according to equation (13) can easily calculate by determining k1 and k2 coefficients taking into account physical and chemical properties, dried material structure. In this approach,  is a function that determines the variation of drying process in the material and time-varying. This function is identifying by empirical method depending on the character of drying process. The effect of EMW in drying process can achieve the fallowing approach.
is a function that determines the variation of drying process in the material and time-varying. This function is identifying by empirical method depending on the character of drying process. The effect of EMW in drying process can achieve the fallowing approach.
2.2. Analysis of the effect of EMW’s drying process If we have taking into account that water is essentially chemical composition of the dried materials, we can assumed that these materials are essentially non-magnetic or very weak magnetic (diamagnetic). Hence, magnetic permeability of the dried material becomes  H/m. The other hand, since they have a certain electrical conductivity, dried material can be assumed that a partially conductive ambient. In this instance, Maxwell’s equations are written as follows by assuming
H/m. The other hand, since they have a certain electrical conductivity, dried material can be assumed that a partially conductive ambient. In this instance, Maxwell’s equations are written as follows by assuming  [5-9].
[5-9].
 (14)
(14)
 (15)
(15)
 (16)
(16)
In the event of (z-dimension) one-dimension propagation of electromagnetic waves, charges in fields of E and H in these equations are obtained as follows;
 (17)
(17)
 (18)
(18)
EMW’s wave impedance ZD sprawling in the z direction in dried ambient and diffusion coefficient γ,
 (19)
(19)
 (20)
(20)
as are determined. Here, α is wave extinction coefficient and β is phase constant. If these expressions taken into consideration, solution of the wave equation (equation (17) and equation (18)) is written as follows .
 (21)
(21)
 (22)
(22)
Here,
 (23)
(23)
Propagation velocity of the electromagnetic wave and wave length is calculated as follows.
 (24)
(24)
According to wave parameters contained in equation (21) is dependent on the physical characteristics of dried material, these parameters will have different values in distinct process. For this reason, the corrected values of these parameters should be determined according to the measurement taken from drying experiments. For this purpose, drying power formed by the electromagnetic wave must be measured. This process can be done using a special cell designed in drying mechanism (Figure 4).
In this drying cell given in description of the next section can readily be determined change over time the electrical conductivity of the dried material. According to these results, the proportion of ( ) in dried system can be evaluated and cut-off frequency fc required by drying system can be determined. Cut-off frequency and physical properties of the dried material, blow out and phase constant can be easily calculated,
) in dried system can be evaluated and cut-off frequency fc required by drying system can be determined. Cut-off frequency and physical properties of the dried material, blow out and phase constant can be easily calculated,
 (25)
(25)
 (26)
(26)
After calculating these parameters, changes in areas of E and H from equation (12) can be easily determined. After determination of the E and H fields, the contribution of EMW in drying process and proportion of the change in moisture by the effect of this contribution can be calculated. The contribution of the heat shown the drying process of EMW can be evaluated by Poynting vector.
 (27)
(27)
Calculated from the real component of this vector producing the effects of thermal drying process is part of the active power.
 (28)
(28)
Here, H* is the complex conjugate of the H magnetic field strength. Heat energy generated the dried materials of EMW,
 (29)
(29)
as determined. Where E and H* fields are determined according to the calculated values in Equation (21).
Heat generated by the induction in dried material,

It can be calculated according to the power. Wherein B is the magnetic field density and is calculated accord

Figure 4. Block diagram of the cell designed for the determination of drying power.
ing to equation (29). Taking into consideration parameters of EMW, proportion of the change in moisture by the effect of EMW using the π theorem can be modeled as follows,
 (30)
(30)
Here f = 100 kHz is cut-off frequency of wave. Thus take into consideration Equation (13) and Equation (30), variation of total moisture concentration in drying process is obtained in the following format from M in (4).
 (31)
(31)
3. Experiments Examine the effect of drying process of electromagnetic wave has been made in laboratory drying machine specially designed . The main elements of drying cell and drying system has been shown in Figure 5.
Material sample 4 dried in drying regions which has cylindrical form has been placed. Drying pipe 1 has been made from insulator and non-magnetic material (plastic). Electrodes of 2 have been placed in the inner walls of the pipe. The geometry of electrodes and dimensions has been selected so that; electric field E that these electrodes are formed get a homogeneous spread on the dried material. The magnetic field (B) in drying region is created by solenoid 3 wrapped on the drying pipe. Dried sample and solenoid 3 according to dimensions of the drying system be considered as a long solenoid. Therefore, B field formed in drying pipe of solenoid 3 has been evaluated as homogenous area. The effect of electromagnetic field on the dried sample 4 has been implemented as electric (E) and magnetic fields (B) that direction perpendicular to each other due to the structure of 2’s electrodes and 3’s solenoid. The air which have capable maintaining constant temperature (T = constant) within the drying pipe during drying has been blow as a laminar at a constant speed (V = constant). Dried sample 4 which have dimensions of 2δ × b × L are placed on the center axis x of drying pipe and right in the middle. Thus, the dried sample 4 remains under the influence of E and B fields of air blown continuously during the drying. E and B fields and acting on EMW can be controlled and adjusted by the external electric circuit. The geometry of sample 4 dried periodically during drying is examined and mass change is measured.
The power of drying system to assess the effect of EMW is determined by measurement of the drying cell shown in figure 4. For this purpose, sample dried in drying process is measured resistance and permeability. Drying cell in figure 3 has been created that two electrodes thickness of 1 mm, ohmmeter which is connected to copper conductor wire of these electrodes. Copper electrodes have been combined with springs to provide the flexibility of drying cell volume. Dried sample 2 is placed between the copper electrodes. Varying resistance and permeability with volume change as a result of drying process of dried material can be continuously measured by ohmmeter 4.
4. Result and Discussion Drying of different materials have been made for assess the impact of the drying events of electromagnetic wave and comparisons of the results obtained from theoretical models. The role of the effect of EMW in drying process has been determined by changing the temperature of the environment. Potato slices as the dried material sample has been used. Potato slice which have dimensions (1 mm × 3.6 mm × 5.2 mm) is placed in drying pipe 1 as shown in figure 5. The drying process has been made both under the influence of EMW and without EMW. The parameters of external search which are constitute of EMW have been taken U = 30 V, I = 0.275 A, f = 30 kHz. Rate and temperature of the blown air have been Va = 2 m/s, T = 40˚C respectively. Resistance or permeability change of sample that is periodically dried during the drying has been measured by the cell schema in figure 3 and the results obtained are provided in Table 1.
Cut-off frequency of EMW in drying process,
 (32)
(32)

Figure 5. Principle diagram of drying mechanism; 1—non-magnetic cylindrical drying pipe, 2—electrodes, 3—swathe-solenoid, 4—dried material sample.

Table 1. Measurement of resistance and permeability changes in drying of potato samples.
Taking into consideration the inequality, cut-off frequency determined as,
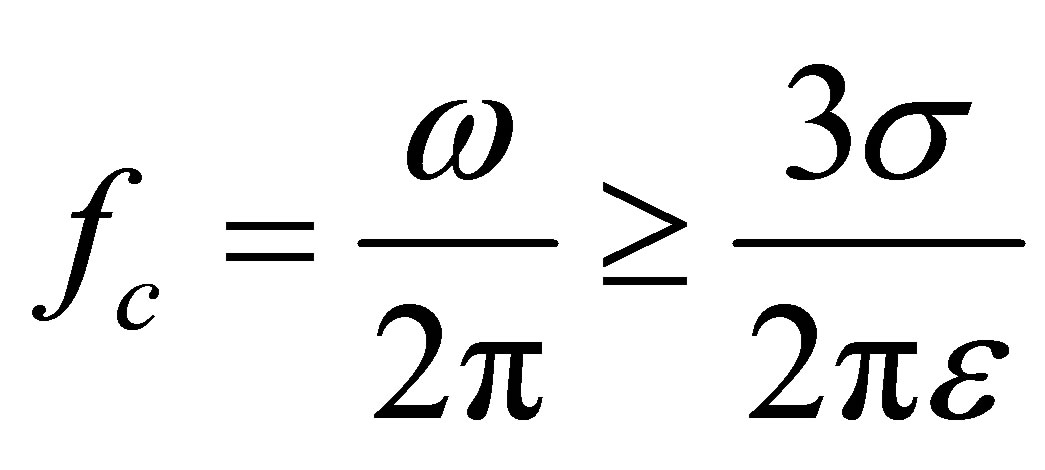 (33)
(33)
Cut-off frequency values stemming from the change permeability of the dried material with time has been shown in Table 2. Here, for a slice of wet potato, εr = 140, ε0 = 8.854 × 10−12 F/m, ε = εrε0 = 1.24 × 10−9 F/m, µ =µ0 = 4π × 10−7 H/m are assumed.
The effect of frequencies over f = 17 Hz after 4 hours of drying process, the effect of frequencies over f = 4 kHz after than 4.5 hours become zero. In other words, potato slice dried under the above conditions indicate a very weak conductivity in order to EMW in frequencies above approximately f = 17 kHz. In this event, the effects on drying process of EMW enough to be neglected weak. According to permeability of dried material is relatively high at the inception of drying material, EMW varying with frequency have an active part in drying process. Thought drying process is formation by the influence of both wave frequency and heat, wave frequency affecting the drying process may be selected around f = 15 kHz or less than f = 17 kHz.
Due to the E and H fields are E = 300 V/m, H = 200 A/m in the absence of the dried sample in the drying pipe at 313 K, characteristic impedance or wave impedance of the media is become as fallow,
 (34)
(34)
Change over time of wave impedance of potato slice such as the default partially the conducting medium calculated making use of Table 1 are shown in Table 3.
In consideration of these changes, extinction and phase coefficients of the EMW calculated according to min (29) are presented in Table 4. As shown in table 2 after the time t = 4.5 hours, extinction coefficient (α) reaches the negligible lower values. This result means that the resistance to the effect of EMW-dried material.
Change over time of moisture content obtained from drying the potato slice in figure 6 has been shown. In figure 6, the absence of action by EMW in the first curve (f = 0) and the effect of EMW in drying process in the second curve (f = 5 kHz) have been shown. a(t) coefficients which is characterizing the change with time of dif .

Table 2. Cut-off frequency changes over with the time in drying of potato slice.

Table 3. Change over time of wave impedance.

Table 4. Change over time of extinction and phase constant of EMW.

Figure 6. Moisture and inner temperature profiles of potato during drying (T = 313 K˚, Va = 2 m/s) (1—without EMW, 2—with EMW, 3—change of the inner temperature in drying sample; continuous lines are theoretical and symbols are experimental results).
fusion coefficient in these process have been modeled as follows;
 (35)
(35)
 (36)
(36)
α1(t) and α(t) at issue in equation (35) and equation (36) are expressions that takes into account changes with over time of diffusion coefficient. α1(t) is diffusion coefficient of convection drying and α(t) is considers both the effect of convection and the effect of electromagnetic fields. These parameters are varying depending on nonlinear with time and temperature. In generally, determination of these parameters is virtually impossible in theory. Therefore, these parameters are experimentally obtained from the analysis of experimental data as dependently on the character of the drying process.
As shown in figure 6, drying process began to develop more rapidly from the first moment the effect of EMW. For example, although for the reduction %50 of humidity ratio in classical drying process need t = 5 h, this period time has been shortened as t = 4 h by the application of EMW. Therefore, drying process of potato slice by the effect of EMW has been effectively accelerated. As shown in figure 6, the results obtained from experiments in drying process provide good agreement with theoretical model presented in this study. This result also shows that the presented theoretical model can be used to model in the drying process. The curve which is number three is shown the heat exchange in this example in the drying process of potato slice.
In figure 7, the results of drying process without the influence and influence of the EMW at T = 313 K of potato slice are provided. The parameters of EMW have been selected the same as the ones used in figure 6. But the wave frequency have been adjusted as f = 10 kHz. As shown in figure, moisture content of potato slice has been decreased more rapidly with increasing temperature and drying process has decelerated. The effect of EMW on drying process under the same conditions remains approximately the same. Despite this the effect of EMW on drying process with increasing frequency has provided to be faster of this process. Although 4 hours needed to decrease fifty percent according to the first position of humidity ratio in classic drying process, this process with the effect of EMW which f = 10 Hz has been around t = 3.2 hours.
The results of the drying process with the effect of EMW and without the influence of EMW of potato slice has been presented in figure 8. As a result of the increase in the frequency of EMW along with increasing of heat, drying process has been accelerated. Although it should at t = 3.4 h by the classical method for the reduction of %50 moisture rate, this process is reduced as t = 2.5 h by the effect of EMW having f = 100 kHz frequency.
In other words, drying time in all conditions by the effect of EMW has been visibly decreased. This result proves that advantage and an effective role in drying process of EMW. On the other hand, exchange 20-fold of drying frequency by the effect of EMW have provided about 1.8-fold reduction in drying process. Therefore, in drying process by the effect of EMW as predicted expectations according to results in theoretical reviewers, wave frequency is located in an effective factor. In case of further raise the frequency of the EMW (MHz-GHz at around), conversion of microwave heating process rather than drying of this process will be caused.
5. Conclusions The theoretical and experimental investigations of the effect of the electromagnetic wave in the solid material drying have been able to arrive at the following conclusions.
1) The effect of electromagnetic fields in drying process remains as an important issue of the agenda and the results of theoretical and experimental investigations are presented in the literature. Microwave electromagnetic fields are influenced by the structure of substance, so the use of this model is limited in drying process of the food. For this reason, use of the weak and medium-frequency of electromagnetic waves is foreseen to accelerate the drying process of porous food materials.
2) Experimental investigations of heat transfer in the dried material allow obtaining approximately the expression of mass conservation equation for accelerating the drying process under the influence of electromagnetic wave. The equation obtained from correction of empirical coefficients contained in this equation according to characteristic of the drying process and the physical structure of the material can be used for drying process

Figure 7. Moisture and inner temperature profiles of potato during drying (T = 323 K˚, Va =2 m/s) (1—without EMW, 2—with EMW, 3—change of the inner temperature in drying sample; continuous lines are theoretical and symbols are experimental results).
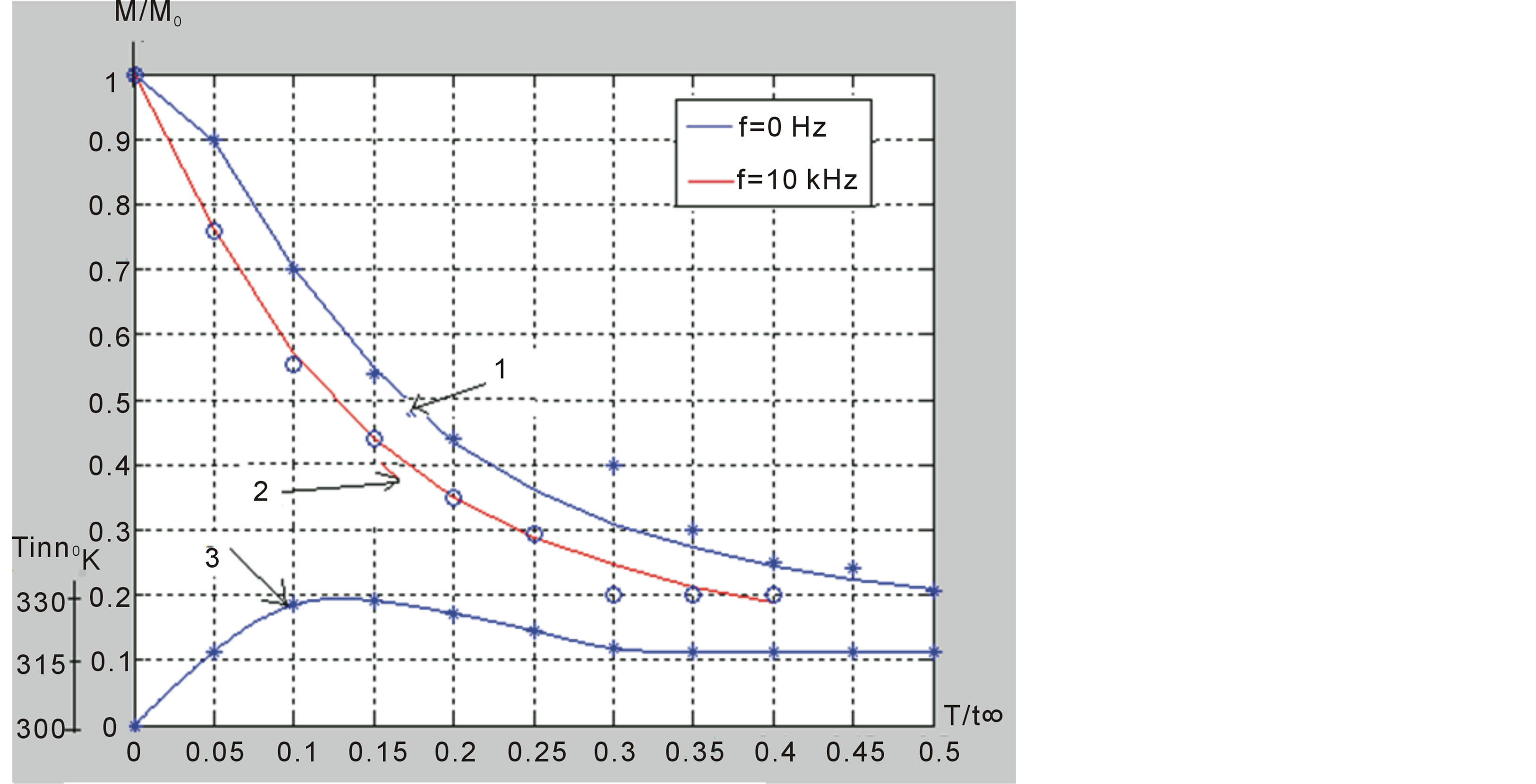
Figure 8. Moisture and inner temperature profiles of potato during drying (T = 333 K˚, Va=2 m/s) (1—without EMW, 2—with EMW, 3—change of the inner temperature in drying sample; continuous lines are theoretical and symbols are experimental results).
for many different food materials.
3) The use of model and concepts well researched in various areas of science to examine the effect of electromagnetic waves in drying process can provide a lot of advantages. The use of electrical circuit theory and π theorem enables to easily model the event of heat and mass transfer in drying process.
4) According to the results of theoretical and experimental investigations, the frequency of electromagnetic wave which is accelerating the drying process of dried material is found to be 10 - 11 kHz and low frequencies. The effects of electromagnetic waves which have f = 20 kHz and higher values at low frequencies have been observed to be effective in the first stage of drying process.
5) Theoretical and experimental results which are obtained have shown a minor disagreement. The cause of these errors occurs from being the different structure and physical properties of dried material. Therefore, the theoretical model which is presented allows taking into account a good enough approach to the effect of electromagnetic waves in drying process.
6) The mechanism of action of the drying process with the electromagnetic field and waves in experiments is foreseen to complete removal of moisture rate in the material in order to evaluate all aspects. Drying the certain humidity of the material in industry environment is required. The graphs which are obtained allow determining the moisture content of material at the different stages of the drying process having regards to the initial mass of dried material. For this purpose, it is useful to be preferred as the diffusion coefficient is time-varying function.
7) Theoretical and experimental results which are presented in accordance with a good adaptation of the model taking into account the drying conditions also contemplate the use and considerations for drying of a broad spectrum of foods.
References
Cemeroglu, B. and Acar, J. (1986) Fruit and vegetable processing technology. Ankara.
Arthur, J.C. and McLe More, T.A. (1955) Sweet potato dehydration. Effect of processing conditions and variety of dehydrated products. Journal of Agricultural Food Chemistry, 3, 782-787. http://dx.doi.org/10.1021/jf60055a007
Cording, J., Willard, M., Eskew, R.K. and Sullivan, J.F. (1957) Advanced in the dehydration of mashed potatoes. Food Technology, 11, 236-240.
Molatson, L.J., Spadaro, L.J., Roby, M.T. and Lee, F.H. (1962) Dehydrated diced sweet potatoes a pilot plant process and product evaluation. Food Technology, 16, 101-104.
Aladjadjyan, A. and Vlieva, T. (2003) Influence of stationary magnetic field on the early of the development of tobacco seeds. Journal of European Agriculture, 4, 131-137.
Tayaraman, K. and Gupta, D.K. (2005) Drying of fruits and vegetables. In: Handbook of Industrial Drying, Merket-Dekker, New York, 643-690.
Mc Minn, W.A. and Magee, T.R. (1997) Physical characteristics of dehydrated potatoes. Journal of Food Engineering, 33, 37-48. http://dx.doi.org/10.1016/S0260-8774(97)00039-3
Vilkov, G.A. and Zabelina, T.N. (1996) Diffusion in a porous system in grossed electric and magnetic fields. Journal of engineering Physics and Thermophysics, 31, 1295-1300.
Kelbaliyev, G.I. and Memmedov, A. (2009) The time depending distribution function and sedimentation properties of dispersion particles. Journal of Dispersion Science and Technology, 30, 1073-1078. http://dx.doi.org/10.1080/01932690802598762
Sadek, S.E., Fax, R.G. and Hurwitz, M. (1972) The influence of electrical fields on convective heat and mass transfer from a horizontal surface under forced convection. Journal of Heat Transfer, 94, 144-148. http://dx.doi.org/10.1115/1.3449885
Knorr, D. and Angebach, A. (1998) Impact of high electric field pulses on plant membrane permecabilisation. Trend in Food Science and Technology, 9, 185-191. http://dx.doi.org/10.1016/S0924-2244(98)00040-5
Jezek, D., Tripalo, B., Karlovic, D., Vikic-Topic, D. and Herceg, Z. (2006) Modeling of convective carrot drying. Croatuca Chemica Acta, 79, 385-395.
Karim, M.A. and Hawlader, M.N.A. (2005) Drying characteristics of banana: Theoretical modeling and experimental validations. Journal of Food Engineering, 70, 35-45. http://dx.doi.org/10.1016/j.jfoodeng.2004.09.010
Rotanadechoab, P., Aokib, K. and Akahoreb, M.A. (2001) Numerical and experimental study of microwave drying using a rectangular waveguide. Drying Technology, 19, 2209-2234. http://dx.doi.org/10.1081/DRT-100107495
Fortes, M. and Okos, M.R. (1980) Drying theories: Their bases and limitations as applied to foods and grains. In: Mujumder, A.S., Ed., Advances in Drying, 1, Hemisphere, Washington DC, 119-154.
Luikov, A.V. (1975) Systems of differential equations of heat and mass transfer in capillary-porous bodies (review). International Journal of Heat and Mass Transfer, 18, 1-14. http://dx.doi.org/10.1016/0017-9310(75)90002-2
Rossen, T.L. and Hayakawa, K. (1977) Simultaneous heat and mass transfer in dehydrated food: A review of theoretical models. AICHE Symposium, 73, 71-86.