Uniqueness of Meromorphic Functions of Differential Polynomials Sharing Two Values IM ()
of the meromorphic function  and by
and by  any quantity satisfying
any quantity satisfying  as
as 
possibly outside a set of finite linear measure.  denotes the truncated counting function bounded by
denotes the truncated counting function bounded by . Moreover,
. Moreover,  denotes the greatest common divisor of positive integers
denotes the greatest common divisor of positive integers .
.
For the sake of simplicity, let  be a nonnegative integer,
be a nonnegative integer,  be complex constants. Define
be complex constants. Define
 (1.1)
(1.1)
In 1929, Nevanlinna [1] proved the following well-know result which is the so called Nevanlinna five values theorem.
Theorem A Let  and
and  be two non-constant meromorphic functions. If
be two non-constant meromorphic functions. If  and
and  share five distinct values IM, then
share five distinct values IM, then .
.
Moreover, he got.
Theorem B Let  and
and  be two distinct non-constant meromorphic functions and
be two distinct non-constant meromorphic functions and  be four distinct values. If
be four distinct values. If  and
and  share
share  CM, then
CM, then  is a Mobius transformation of
is a Mobius transformation of .
.
In 1976, L. Rubel asked the following question:
Whether CM can be replaced by IM in the hypothesis of Theorem A with the same conclusion or not?
In 1979, G. G. Gundersen [2] gave a negative answer for this question by the following counterexample:
 ,
,
where  is a non-constant entire function. It is easy to verify that
is a non-constant entire function. It is easy to verify that  and
and  share the four values
share the four values , where none of the four values are shared CM, and
, where none of the four values are shared CM, and  is not a Mobius transformation of
is not a Mobius transformation of .
.
On the other hand, G. G. Gundersen [3] proved the following result which is an improvement of Theorem B. Theorem C. If two distinct non-constant meromorphic functions share two values CM and share two other values IM, then the functions share all four values CM (hence the conclusions of Theorem B hold).
In this paper, we shall show that similar conclusions hold for certain types of differential polynomials when they share two values IM.
Theorem 1.1 Let  and
and  be two non-constant meromorphic functions,
be two non-constant meromorphic functions,  , and
, and  be
be
three integers with  and
and  be defined as in (1.1). If
be defined as in (1.1). If  and
and 
share 1 and  IM, then
IM, then
1) when ,
, ;
;
2) when , one of the following two cases holds:
, one of the following two cases holds:
3)  for a constant
for a constant  such that
such that ,
,
4) , where
, where 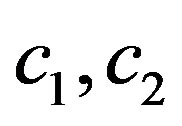 and
and  are three constants satisfying
are three constants satisfying
 .
.
Remark 1.1 “ and
and  share
share  IM”
IM” 
 and
and  share
share  IM”. Moreover,
IM”. Moreover,
from , one cannot get
, one cannot get  for some constant
for some constant . For example, let
. For example, let ,
,
 , then
, then  where
where  is a non-constant meromorphic function. Obviously,
is a non-constant meromorphic function. Obviously,  for some canstant
for some canstant  but
but .
.
Now we give some corollaries of Theorem 1.1. Corollary 1.2 and Corollary 1.3 improve Theorems D and E, respectively.
Corollary 1.2 Let  and
and  be two non-constant meromorphic functions, and let
be two non-constant meromorphic functions, and let  be two positive
be two positive
integers with . If
. If  and
and  share 1 IM,
share 1 IM,  and
and  share
share  IM, then either
IM, then either , where
, where  and
and  are three constants satisfying
are three constants satisfying , or
, or
 for a constant
for a constant  such that
such that .
.
Corollary 1.3 Let  and
and  be two non-constant meromorphic functions satisfying
be two non-constant meromorphic functions satisfying , and let
, and let  be two positive integers with
be two positive integers with . If
. If  and
and  share 1 IM,
share 1 IM, 
and  share
share  IM, then
IM, then .
.
Corollary 1.4 Let  and
and  be two non-constant meromorphic functions, and let
be two non-constant meromorphic functions, and let  be two positive integers with
be two positive integers with ,
,  be a nonzero constant. If
be a nonzero constant. If  and
and 
share 1 IM,  and
and  share
share  IM, then
IM, then  for some constant
for some constant  such that
such that , where
, where
 .
.
Theorem 1.1 generalizes the following result that was obtained by Zhang, Chen and Lin [4].
Theorem D Let  and
and  be two non-constant entire functions. Let
be two non-constant entire functions. Let , and
, and  be three positive integ-
be three positive integ-
ers with  and let
and let  or
or , where
, where  are complex constants. If
are complex constants. If  and
and  share 1 CM, then
share 1 CM, then
1) when , either
, either  for a constant
for a constant  such that
such that , where
, where ,
,  for some
for some , or
, or  and
and  satisfy the algebraic
satisfy the algebraic
equation ,
,
where ;
;
2) when , either
, either , where
, where  and
and  are three constants satisfying
are three constants satisfying , or
, or  for a constant
for a constant  such that
such that .
.
Corollaries 1.2-1.4 greatly improve the following result that was obtained by Liu [5] by reducing the lower bound of . Moreover, the proofs of Corollaries 1.2 - 1.4 fill some gaps appeared in the proof of Theorem E.
. Moreover, the proofs of Corollaries 1.2 - 1.4 fill some gaps appeared in the proof of Theorem E.
Theorem E Let  and
and  be two non-constant meromorphic functions, and let
be two non-constant meromorphic functions, and let , and
, and  be three
be three
positive integers with , and
, and ,
,  be two constants such that
be two constants such that . If
. If
 and
and  share 1 IM,
share 1 IM,  and
and  share
share  IM, then\\
IM, then\\
1) when , If
, If  and
and , then
, then .
.
If  and
and , then
, then ;
;
2) when , if
, if  and
and , then either
, then either , where
, where  is a constant satisfying
is a constant satisfying , or
, or , where
, where  and
and  are three constants satisfying
are three constants satisfying
 or
or  Here,
Here,  , where
, where
 if
if ,
,  if
if .
.
2. Preliminary Lemmas
Let
 (2.1)
(2.1)
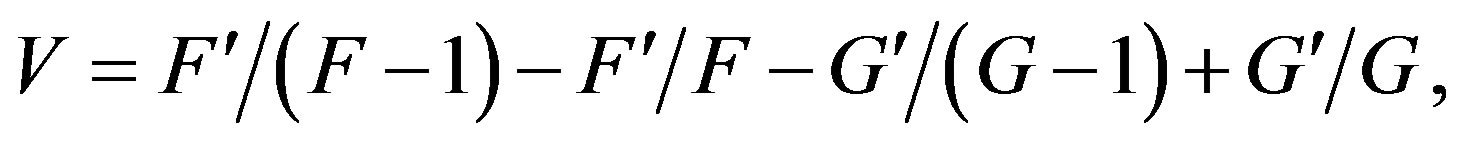 (2.2)
(2.2)
where  and
and  are meromorphic functions.
are meromorphic functions.
Lemma 2.1 [6] Let  be a non-constant meromorphic function and let
be a non-constant meromorphic function and let  be
be
small functions with respect to . Then
. Then

Lemma 2.2 [7] Let  be a non-constant meromorphic function,
be a non-constant meromorphic function, 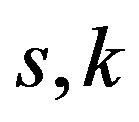 be two positive integers. Then
be two positive integers. Then


Lemma 2.3 [8-10] Let  be a non-constant meromorphic function, and let
be a non-constant meromorphic function, and let  be a positive integer. Suppose that
be a positive integer. Suppose that , then
, then

By using the similar method to Banerjee [11, Lemma 2.14], we can prove the following Lemma.
Lemma 2.4 Let ,
,  and
and  be defined as in (2.1). If
be defined as in (2.1). If  and
and  share 1 CM and
share 1 CM and  IM, and
IM, and , then
, then , and
, and

the same inequality holding for .
.
Lemma 2.5 [12] Let ,
,  and
and  be defined as in (2.2). If
be defined as in (2.2). If  and
and  share
share  IM, and
IM, and , then
, then .
.
Lemma 2.6 [13] If  and
and  share 1 IM, then
share 1 IM, then
 .
.
Lemma 2.7 Let ,
,  be two non-constant meromorphic functions,
be two non-constant meromorphic functions,  be defined as in (2.2), where
be defined as in (2.2), where
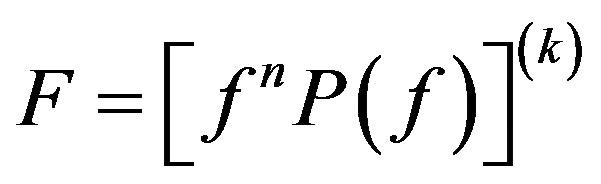 ,
,  ,
,  is defined as in (1.1),
is defined as in (1.1),  ,
,  and
and  are three in-
are three in-
tegers. If ,
,  and
and  share 1 CM and
share 1 CM and  IM, then
IM, then
 (2.3)
(2.3)
Proof Since ,
,  and
and  share
share  IM, suppose that
IM, suppose that  is a pole of
is a pole of  with multiplicity
with multiplicity , a pole of
, a pole of  with multiplicity
with multiplicity , then
, then  is a pole of
is a pole of  with multiplicity
with multiplicity , a pole of
, a pole of  with
with
multiplicity , thus
, thus  is a zero of
is a zero of  with multiplicity
with multiplicity
 , and
, and  is a zero of
is a zero of 
with multiplicity , hence
, hence  is a zero of
is a zero of  with multiplicity at least
with multiplicity at least
 . So
. So
 (2.4)
(2.4)
By the logarithmic derivative lemma, we have . Note that
. Note that  and
and  share 1
share 1
IM, by Lemma 2.6, so we have
 (2.5)
(2.5)
From (2.4) and (2.5) we get (2.3). This proves Lemma 2.7.
Lemma 2.8 [14] Let  and
and  be two non-constant meromorphic functions, and
be two non-constant meromorphic functions, and  be two
be two
positive integers. If , then
, then  for a constant
for a constant  such that
such that .
.
By the same reason as in Lemma 5 of [8], we obtain the following lemma.
Lemma 2.9 Let  and
and  be two non-constant meromorphic functions. Let
be two non-constant meromorphic functions. Let  be defined as in (1.1),
be defined as in (1.1),
and , and
, and  be three integers with
be three integers with . If
. If , then
, then .
.
Lemma 2.10 [15] Let  and
and  be non-constant meromorphic functions,
be non-constant meromorphic functions,  be two positive integers with
be two positive integers with , and let
, and let  be defined as in (1.1),
be defined as in (1.1),  be a small function with respect to
be a small function with respect to 
with finitely many zeros and poles. If ,
,  and
and  share
share  IM, then
IM, then 
is reduced to a nonzero monomial.
Use the proof of Theorem 3 in [15] and we obtain.
Lemma 2.11 Let  and
and  be non-constant meromorphic functions,
be non-constant meromorphic functions,  be two positive integers with
be two positive integers with
 . If
. If ,
,  and
and  share
share  IM, then
IM, then , where
, where  and
and  are three constants satisfying
are three constants satisfying .
.
Lemma 2.12 [16] Let  and
and  are relatively prime integers, and let
are relatively prime integers, and let  be a complex number such that
be a complex number such that . Then there exists one and only one common zero of
. Then there exists one and only one common zero of  and
and .
.
3. Proof of Theorem 1.1
Let ,
,  ,
,  ,
,  , then
, then  and
and  share 1 IM and
share 1 IM and 
IM. Suppose that , then
, then , and
, and .
.
Case 1. . By Lemma 2.4 we have
. By Lemma 2.4 we have
 (3.1)
(3.1)
By Lemma 2.2 with , we obtain
, we obtain
 (3.2)
(3.2)
and
 (3.3)
(3.3)
Combining (3.1) - (3.3) gives

It follows from Lemma 2.1 and the above inequality that
 (3.4)
(3.4)
Similarly we have
 (3.5)
(3.5)
Note that . . From (3.4) and (3.5) we deduce that
. From (3.4) and (3.5) we deduce that
 . (3.6)
. (3.6)
Note that  and we get (2.3). By Lemma 2.2 with
and we get (2.3). By Lemma 2.2 with , we obtain
, we obtain
 (3.7)
(3.7)
and
 (3.8)
(3.8)
From (2.3), (3.7) and (3.8) we get
 (3.9)
(3.9)
Combining (3.6) - (3.9) gives
 (3.10)
(3.10)
which is a contradiction since . Thus
. Thus . Similar to the proof of [17, Lemma 3], we obtain
. Similar to the proof of [17, Lemma 3], we obtain
1) , or
, or
2) .
.
By Lemma 2.10, the case of 1) is impossible. By Lemma 2.9, we get  from 2).
from 2).
Case 2. . Similar to the proof of Case 1, we get
. Similar to the proof of Case 1, we get
 , (3.11)
, (3.11)
which is a contradiction since . Thus
. Thus . and we have
. and we have
3) , or
, or
4) .
.
For 3), by Lemma 2.11, we get , where
, where  and
and  are three con-
are three con-
stants satisfying .
.
For 4), By Lemma 2.8, we get  for a constant
for a constant  such that
such that . This completes the proof of Theorem 1.1.
. This completes the proof of Theorem 1.1.
4. Proof of Corollaries 1.2 - 1.4
The proof of Corollary 1.2 is the same to the proof of Case 2 of Theorem 1.1, we only need to let . Thus we omit the proof here.
. Thus we omit the proof here.
Now we prove Corollary 1.3, Let , similar to (3.10), we get
, similar to (3.10), we get
 , (3.12)
, (3.12)
which is a contradiction since . Thus
. Thus  and we have
and we have
1) , or
, or
2) .
.
By Lemma 2.10, the case of (i) is impossible. By Lemma 2.9, we get  from 2).
from 2).
Similar to the proof of Theorem 2 in [14], we get . This proves Corollary 1.3.
. This proves Corollary 1.3.
Next we prove Corollary 1.4.
According to the proof of Case 1 in Theorem 1.1, we have
1) , or
, or
2) .
.
By Lemma 2.10, the case of 1) is impossible. By Lemma 2.9, we get  from 2).
from 2).
Let . If
. If  is not a constant, then substitute
is not a constant, then substitute  into
into  and we get
and we get

where  are distinct roots of the algebraic equation
are distinct roots of the algebraic equation ,
,  are distinct roots of the algebraic equation
are distinct roots of the algebraic equation .
.
Suppose that , then
, then ,
,  , where
, where ,
,  are co-prime integers and
are co-prime integers and ,
,
thus , which implies
, which implies . By Lemma 2.12, there exists one and only one common zero of
. By Lemma 2.12, there exists one and only one common zero of  and
and , namely
, namely . Therefore, there exists at least
. Therefore, there exists at least  of
of  different from
different from . Suppose that
. Suppose that  are different from
are different from , then all zeros of
, then all zeros of  have order of at least m. Applying the second fundamental theorem to
have order of at least m. Applying the second fundamental theorem to  gives
gives

Note that  and we get a contradiction. Thus
and we get a contradiction. Thus  is a constant. From (4.2) we have
is a constant. From (4.2) we have  and
and , thus
, thus  for some constant
for some constant  such that
such that , where
, where . This proves Corollary 1.4.
. This proves Corollary 1.4.
5. Open Problem
For further study, we pose the following. Problem: What form of  implies
implies  for some constant
for some constant ?
?
Let  and
and  be two non-constant meromorphic functions defined in the open complex plane
be two non-constant meromorphic functions defined in the open complex plane . Let
. Let , we say that
, we say that  and
and  share
share  CM (counting multiplicities) if
CM (counting multiplicities) if ,
,  have the same zeros with the same multiplicities and we say that
have the same zeros with the same multiplicities and we say that  and
and  share
share  (ignoring multiplicities) if we do not consider the multiplicities. We denote by
(ignoring multiplicities) if we do not consider the multiplicities. We denote by  the Nevanlinna characteristic function of the meromorphic function
the Nevanlinna characteristic function of the meromorphic function  and by
and by  any quantity satisfying
any quantity satisfying  as
as 
possibly outside a set of finite linear measure.  denotes the truncated counting function bounded by
denotes the truncated counting function bounded by . Moreover,
. Moreover,  denotes the greatest common divisor of positive integers
denotes the greatest common divisor of positive integers .
.
For the sake of simplicity, let  be a nonnegative integer,
be a nonnegative integer,  be complex constants. Define
be complex constants. Define
 (1.1)
(1.1)
In 1929, Nevanlinna [1] proved the following well-know result which is the so called Nevanlinna five values theorem.
Theorem A Let  and
and  be two non-constant meromorphic functions. If
be two non-constant meromorphic functions. If  and
and  share five distinct values IM, then
share five distinct values IM, then .
.
Moreover, he got.
Theorem B Let  and
and  be two distinct non-constant meromorphic functions and
be two distinct non-constant meromorphic functions and  be four distinct values. If
be four distinct values. If  and
and  share
share  CM, then
CM, then  is a Mobius transformation of
is a Mobius transformation of .
.
In 1976, L. Rubel asked the following question:
Whether CM can be replaced by IM in the hypothesis of Theorem A with the same conclusion or not?
In 1979, G. G. Gundersen [2] gave a negative answer for this question by the following counterexample:
 where
where  is a non-constant entire function. It is easy to verify that
is a non-constant entire function. It is easy to verify that  and
and  share the four values
share the four values , where none of the four values are shared CM, and
, where none of the four values are shared CM, and  is not a Mobius transformation of
is not a Mobius transformation of .
.
On the other hand, G. G. Gundersen [3] proved the following result which is an improvement of Theorem B. Theorem C. If two distinct non-constant meromorphic functions share two values CM and share two other values IM, then the functions share all four values CM (hence the conclusions of Theorem B hold).
In this paper, we shall show that similar conclusions hold for certain types of differential polynomials when they share two values IM.
Theorem 1.1 Let  and
and  be two non-constant meromorphic functions,
be two non-constant meromorphic functions,  , and
, and  be three integers with
be three integers with  and
and  be defined as in (1.1). If
be defined as in (1.1). If  and
and 
share 1 and  IM, then 1) when
IM, then 1) when ,
, ;
;
2) when , one of the following two cases holds:
, one of the following two cases holds:
3)  for a constant
for a constant  such that
such that 4)
4) , where
, where 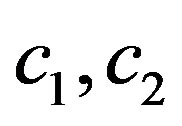 and
and  are three constants satisfying
are three constants satisfying
 .
.
Remark 1.1 “ and
and  share
share  IM”
IM” 
 and
and  share
share  IM”. Moreoverfrom
IM”. Moreoverfrom , one cannot get
, one cannot get  for some constant
for some constant . For example, let
. For example, let ,
,
 , then
, then  where
where  is a non-constant meromorphic function. Obviously,
is a non-constant meromorphic function. Obviously,  for some canstant
for some canstant  but
but .
.
Now we give some corollaries of Theorem 1.1. Corollary 1.2 and Corollary 1.3 improve Theorems D and E, respectively.
Corollary 1.2 Let  and
and  be two non-constant meromorphic functions, and let
be two non-constant meromorphic functions, and let  be two positive integers with
be two positive integers with . If
. If  and
and  share 1 IM,
share 1 IM,  and
and  share
share  IM, then either
IM, then either , where
, where  and
and  are three constants satisfying
are three constants satisfying , or
, or
 for a constant
for a constant  such that
such that .
.
Corollary 1.3 Let  and
and  be two non-constant meromorphic functions satisfying
be two non-constant meromorphic functions satisfying , and let
, and let  be two positive integers with
be two positive integers with . If
. If  and
and  share 1 IM,
share 1 IM, 
and  share
share  IM, then
IM, then .
.
Corollary 1.4 Let  and
and  be two non-constant meromorphic functions, and let
be two non-constant meromorphic functions, and let  be two positive integers with
be two positive integers with ,
,  be a nonzero constant. If
be a nonzero constant. If  and
and 
share 1 IM,  and
and  share
share  IM, then
IM, then  for some constant
for some constant  such that
such that , where
, where
 .
.
Theorem 1.1 generalizes the following result that was obtained by Zhang, Chen and Lin [4].
Theorem D Let  and
and  be two non-constant entire functions. Let
be two non-constant entire functions. Let , and
, and  be three positive integers with
be three positive integers with  and let
and let  or
or , where
, where  are complex constants. If
are complex constants. If  and
and  share 1 CM, then 1) when
share 1 CM, then 1) when , either
, either  for a constant
for a constant  such that
such that , where
, where ,
,  for some
for some , or
, or  and
and  satisfy the algebraic equation
satisfy the algebraic equation where
where ;
;
2) when , either
, either , where
, where  and
and  are three constants satisfying
are three constants satisfying , or
, or  for a constant
for a constant  such that
such that .
.
Corollaries 1.2-1.4 greatly improve the following result that was obtained by Liu [5] by reducing the lower bound of . Moreover, the proofs of Corollaries 1.2 - 1.4 fill some gaps appeared in the proof of Theorem E.
. Moreover, the proofs of Corollaries 1.2 - 1.4 fill some gaps appeared in the proof of Theorem E.
Theorem E Let  and
and  be two non-constant meromorphic functions, and let
be two non-constant meromorphic functions, and let , and
, and  be three positive integers with
be three positive integers with , and
, and ,
,  be two constants such that
be two constants such that . If
. If
 and
and  share 1 IM,
share 1 IM,  and
and  share
share  IM, then\\
IM, then\\
1) when , If
, If  and
and , then
, then .
.
If  and
and , then
, then ;
;
2) when , if
, if  and
and , then either
, then either , where
, where  is a constant satisfying
is a constant satisfying , or
, or , where
, where  and
and  are three constants satisfying
are three constants satisfying
 or
or  Here,
Here,  , where
, where
 if
if ,
,  if
if .
.
2. Preliminary Lemmas
Let
 (2.1)
(2.1)
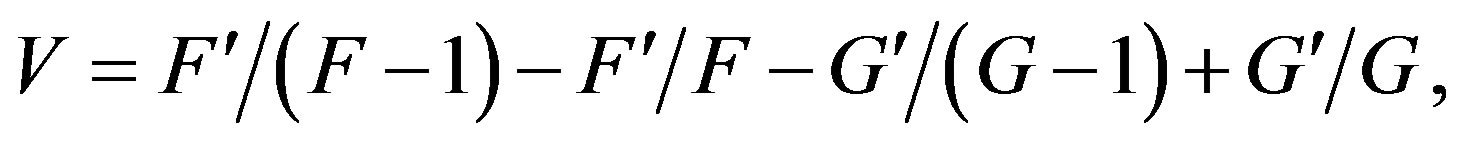 (2.2)
(2.2)
where  and
and  are meromorphic functions.
are meromorphic functions.
Lemma 2.1 [6] Let  be a non-constant meromorphic function and let
be a non-constant meromorphic function and let  be small functions with respect to
be small functions with respect to . Then
. Then

Lemma 2.2 [7] Let  be a non-constant meromorphic function,
be a non-constant meromorphic function, 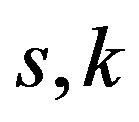 be two positive integers. Then
be two positive integers. Then


Lemma 2.3 [8-10] Let  be a non-constant meromorphic function, and let
be a non-constant meromorphic function, and let  be a positive integer. Suppose that
be a positive integer. Suppose that , then
, then

By using the similar method to Banerjee [11, Lemma 2.14], we can prove the following Lemma.
Lemma 2.4 Let ,
,  and
and  be defined as in (2.1). If
be defined as in (2.1). If  and
and  share 1 CM and
share 1 CM and  IM, and
IM, and , then
, then , and
, and

the same inequality holding for .
.
Lemma 2.5 [12] Let ,
,  and
and  be defined as in (2.2). If
be defined as in (2.2). If  and
and  share
share  IM, and
IM, and , then
, then .
.
Lemma 2.6 [13] If  and
and  share 1 IM, then
share 1 IM, then
 .
.
Lemma 2.7 Let ,
,  be two non-constant meromorphic functions,
be two non-constant meromorphic functions,  be defined as in (2.2), where
be defined as in (2.2), where
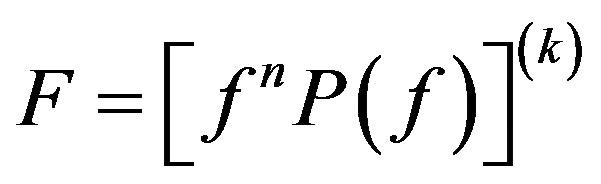 ,
,  ,
,  is defined as in (1.1),
is defined as in (1.1),  ,
,  and
and  are three integers. If
are three integers. If ,
,  and
and  share 1 CM and
share 1 CM and  IM, then
IM, then
 (2.3)
(2.3)
Proof Since ,
,  and
and  share
share  IM, suppose that
IM, suppose that  is a pole of
is a pole of  with multiplicity
with multiplicity , a pole of
, a pole of  with multiplicity
with multiplicity , then
, then  is a pole of
is a pole of  with multiplicity
with multiplicity , a pole of
, a pole of  with multiplicity
with multiplicity , thus
, thus  is a zero of
is a zero of  with multiplicity
with multiplicity
 , and
, and  is a zero of
is a zero of 
with multiplicity , hence
, hence  is a zero of
is a zero of  with multiplicity at least
with multiplicity at least
 . So
. So
 (2.4)
(2.4)
By the logarithmic derivative lemma, we have . Note that
. Note that  and
and  share 1 IM, by Lemma 2.6, so we have
share 1 IM, by Lemma 2.6, so we have
 (2.5)
(2.5)
From (2.4) and (2.5) we get (2.3). This proves Lemma 2.7.
Lemma 2.8 [14] Let  and
and  be two non-constant meromorphic functions, and
be two non-constant meromorphic functions, and  be two positive integers. If
be two positive integers. If , then
, then  for a constant
for a constant  such that
such that .
.
By the same reason as in Lemma 5 of [8], we obtain the following lemma.
Lemma 2.9 Let  and
and  be two non-constant meromorphic functions. Let
be two non-constant meromorphic functions. Let  be defined as in (1.1)and
be defined as in (1.1)and , and
, and  be three integers with
be three integers with . If
. If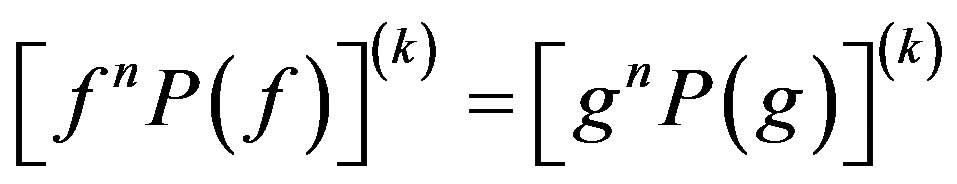 , then
, then .
.
Lemma 2.10 [15] Let  and
and  be non-constant meromorphic functions,
be non-constant meromorphic functions,  be two positive integers with
be two positive integers with , and let
, and let  be defined as in (1.1),
be defined as in (1.1),  be a small function with respect to
be a small function with respect to 
with finitely many zeros and poles. If ,
,  and
and  share
share  IM, then
IM, then 
is reduced to a nonzero monomial.
Use the proof of Theorem 3 in [15] and we obtain.
Lemma 2.11 Let  and
and  be non-constant meromorphic functions,
be non-constant meromorphic functions,  be two positive integers with
be two positive integers with
 . If
. If ,
,  and
and  share
share  IM, then
IM, then , where
, where  and
and  are three constants satisfying
are three constants satisfying .
.
Lemma 2.12 [16] Let  and
and  are relatively prime integers, and let
are relatively prime integers, and let  be a complex number such that
be a complex number such that . Then there exists one and only one common zero of
. Then there exists one and only one common zero of  and
and .
.
3. Proof of Theorem 1.1
Let ,
,  ,
,  ,
,  , then
, then  and
and  share 1 IM and
share 1 IM and 
IM. Suppose that , then
, then , and
, and .
.
Case 1. . By Lemma 2.4 we have
. By Lemma 2.4 we have
 (3.1)
(3.1)
By Lemma 2.2 with , we obtain
, we obtain
 (3.2)
(3.2)
and
 (3.3)
(3.3)
Combining (3.1) - (3.3) gives

It follows from Lemma 2.1 and the above inequality that
 (3.4)
(3.4)
Similarly we have
 (3.5)
(3.5)
Note that . . From (3.4) and (3.5) we deduce that
. From (3.4) and (3.5) we deduce that
 . (3.6)
. (3.6)
Note that  and we get (2.3). By Lemma 2.2 with
and we get (2.3). By Lemma 2.2 with , we obtain
, we obtain
 (3.7)
(3.7)
and
 (3.8)
(3.8)
From (2.3), (3.7) and (3.8) we get
 (3.9)
(3.9)
Combining (3.6) - (3.9) gives
 (3.10)
(3.10)
which is a contradiction since . Thus
. Thus . Similar to the proof of [17, Lemma 3], we obtain 1)
. Similar to the proof of [17, Lemma 3], we obtain 1) , or 2)
, or 2) .
.
By Lemma 2.10, the case of 1) is impossible. By Lemma 2.9, we get  from 2).
from 2).
Case 2. . Similar to the proof of Case 1, we get
. Similar to the proof of Case 1, we get
 , (3.11)
, (3.11)
which is a contradiction since . Thus
. Thus . and we have 3)
. and we have 3) , or 4)
, or 4) .
.
For 3), by Lemma 2.11, we get , where
, where  and
and  are three constants satisfying
are three constants satisfying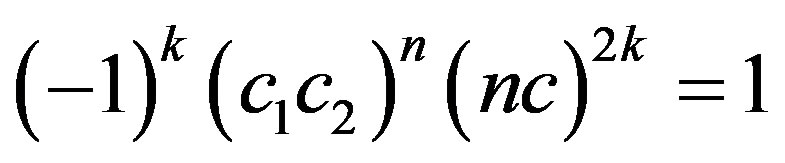 .
.
For 4), By Lemma 2.8, we get  for a constant
for a constant  such that
such that . This completes the proof of Theorem 1.1.
. This completes the proof of Theorem 1.1.
4. Proof of Corollaries 1.2 - 1.4
The proof of Corollary 1.2 is the same to the proof of Case 2 of Theorem 1.1, we only need to let . Thus we omit the proof here.
. Thus we omit the proof here.
Now we prove Corollary 1.3, Let , similar to (3.10), we get
, similar to (3.10), we get
 , (3.12)
, (3.12)
which is a contradiction since . Thus
. Thus  and we have 1)
and we have 1) , or 2)
, or 2) .
.
By Lemma 2.10, the case of (i) is impossible. By Lemma 2.9, we get  from 2).
from 2).
Similar to the proof of Theorem 2 in [14], we get . This proves Corollary 1.3.
. This proves Corollary 1.3.
Next we prove Corollary 1.4.
According to the proof of Case 1 in Theorem 1.1, we have 1) , or 2)
, or 2) .
.
By Lemma 2.10, the case of 1) is impossible. By Lemma 2.9, we get  from 2).
from 2).
Let . If
. If  is not a constant, then substitute
is not a constant, then substitute 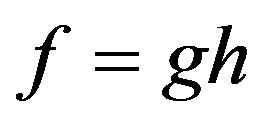 into
into  and we get
and we get

where  are distinct roots of the algebraic equation
are distinct roots of the algebraic equation ,
,  are distinct roots of the algebraic equation
are distinct roots of the algebraic equation .
.
Suppose that , then
, then ,
,  , where
, where ,
,  are co-prime integers and
are co-prime integers and thus
thus , which implies
, which implies . By Lemma 2.12, there exists one and only one common zero of
. By Lemma 2.12, there exists one and only one common zero of  and
and , namely
, namely . Therefore, there exists at least
. Therefore, there exists at least  of
of  different from
different from . Suppose that
. Suppose that  are different from
are different from , then all zeros of
, then all zeros of  have order of at least m. Applying the second fundamental theorem to
have order of at least m. Applying the second fundamental theorem to  gives
gives

Note that  and we get a contradiction. Thus
and we get a contradiction. Thus  is a constant. From (4.2) we have
is a constant. From (4.2) we have  and
and , thus
, thus  for some constant
for some constant  such that
such that , where
, where . This proves Corollary 1.4.
. This proves Corollary 1.4.
5. Open Problem
For further study, we pose the following. Problem: What form of 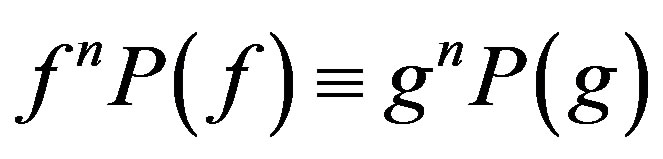 implies
implies  for some constant
for some constant ?
?
Acknowledgements
The author would like to thank the referee for his valuable suggestions.
[1] R. Nevanliana, “Le Theoreme de Picard-Borel at la Theorie des Fonctions Meromorph,” Gauthier-Villars, Paries, 1929.
[2] G. G. Gundersen, “Meromorphic Functions That Share Three or Four Values,” Journal of the London Mathematical Society, Vol. 20, No. 2, 1979, pp. 457-466. http://dx.doi.org/10.1112/jlms/s2-20.3.457
[3] G. G. Gundersen, “Meromorphic Functions That Share Four Values,” Transactions of the American Mathematical Society, Vol. 277, No. 2, 1983, pp. 545-567.
[4] X. Y. Zhang, J. F. Chen and W. C. Lin, “Entire or Meromorphic Functions Sharing One Value,” Computers & Mathematics with Applications, Vol. 56, No. 7, 2008, pp. 1876-1883. http://dx.doi.org/10.1016/j.camwa.2008.04.008
[5] L. P. Liu, “Uniqueness of Meromorphic Functions and Differential Polynomials,” Computers & Mathematics with Applications, Vol. 56, No. 12, 2008, pp. 3236-3245. http://dx.doi.org/10.1016/j.camwa.2008.09.020
[6] C. C. Yang, “On Deficiencies of Differential Polynomials II,” Mathematische Zeitschrift, Vol. 125, No. 2, 1972, pp. 107-112. http://dx.doi.org/10.1007/BF01110921
[7] W. C. Lin and H. X. Yi, “Uniqueness Theorems for Meromorphic Functions,” Indian Journal of Pure and Applied Mathematics, Vol. 35, No. 2, 2004, pp. 121-132.
[8] W. K. Hayman, “Meromorphic Functions,” Clarendon Press, Oxford, 1964.
[9] C. C. Yang and H. X. Yi, “Uniqueness Theory of Meromorphic Functions,” Kluwer Academic Publication, Dordrecht, 2003. http://dx.doi.org/10.1007/978-94-017-3626-8
[10] L. Yang, “Value Distribution Theory,” Springer-Verlag, Berlin, 1993.
[11] A. Banerjee, “Meromorphic Functions Sharing One Value,” International Journal of Mathematics and Mathematical Sciences, Vol. 2005, No. 22, 2005, pp. 3587-3598. http://dx.doi.org/10.1155/IJMMS.2005.3587
[12] H. X. Yi, “Meromorphic Functions That Share Three Sets,” Kodai Mathematical Journal, Vol. 20, No. 1, 1997, pp. 22-32. http://dx.doi.org/10.2996/kmj/1138043717
[13] H. X. Yi, “Meromorphic Functions That Share One or Two Values. II,” Kodai Mathematical Journal, Vol. 22, No. 2, 1999, pp. 264-272. http://dx.doi.org/10.2996/kmj/1138044046
[14] J. F. Xu, F. Lv and H. X. Yi, “Fixed-Points and Uniqueness of Meromorphic Functions,” Computers & Mathematics with Applications, Vol. 59, No. 1, 2010, pp. 9-17. http://dx.doi.org/10.1016/j.camwa.2009.07.024
[15] X. B. Zhang and J. F. Xu, “Uniqueness of Meromorphic Functions Sharing a Small Function and Its Applications,” Computers & Mathematics with Applications, Vol. 61, No. 3, 2011, pp. 722-730. http://dx.doi.org/10.1016/j.camwa.2010.12.022
[16] Q. C. Zhang, “Meromorphic Functions Sharing Three Values,” Indian Journal of Pure and Applied Mathematics, Vol. 30, No. 7, 1999, pp. 667-682.
[17] C. C. Yang and X. H. Hua, “Uniqueness and Value-Sharing of Meromorphic Functions,” Annales Academice Scientiarum Fennicæ Mathematica, Vol. 22, No. 2, 1997, pp. 395-406.