Tests for Two-Sample Location Problem Based on Subsample Quantiles ()
1. Introduction
Two-sample location problem is one of the extensively studied problems in the literature. There are many nonparametric tests available in literature for the above problem, their relative efficiency and suitability depending on the nature of the (unknown) underlying distribution F. For this problem, for example there is a whole class of locality asymptotically most powerful (distribution free) linear rank tests for each specified distribution F, which included the well known Mann-Whitney, normal score and median tests among many others ([1], Ch-III, 1.1). While the median test is particularly effective for heavy tailed symmetric distributions, the normal score and Mann-Whitney tests are relatively even handed and reasonably effective for moderately heavy tailed bell shaped distributions. During the last decade or so, new classes of tests based on the so called subsample approach have been proposed for the above problem, notable among them being Deshpande and Kochar [2], Stephenson and Gosh [3], Shetty and Govindarajulu [6], Shetty and Bhat [7] and Ahmad [8]. While Shetty and Govindarajulu [6] and Shetty and Bhat [7] based their tests on subsample medians which tend to emphasize the centre of the underlying distributions, the other two are based on statistics involving subsample extrema with the object of gaining more information from the tails of sampled distributions. The results of these papers demonstrate that the subsample approach, applied selectively, does help to improve upon the efficiency performance of the tests mentioned in the preceding paragraph in an overall sense. For example, in consonance with the efficiency results noted in the last paragraph, Shetty and Govindarajulu [6] test performs on one hand better than the MannWhitney test for heavy-tailed distributions, while performing better than the median test for light-tailed distributions on the other. Deshpande and Kochar [2] test, on the other hand, being sensitive to light-tailed distributions, performs substantially better than Mann-Whitney test for such underlying distributions and some what better for normal, while maintaining reasonable level of efficiency under heavy-tailed distributions. Stephenson and Ghosh [3] and Ahmad [8] tests are also relatively more sensitive than the Mann-Whitney test but less than the Deshpande and Kochar [2] test to the light-tailed distributions. Recently, Xie and Priebe [9] proposed a generalization of Mann-Whitney test which includes many existing tests as its members. They studied the asymptotic relative efficiencies of the members of the proposed class of tests and investigated the optimum member (having maximum efficacy) in the class of tests.
Let 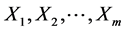 and
and 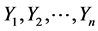 be two independent random samples of i.i.d. observations from two populations with continuous distribution functions (d.f’s), from
be two independent random samples of i.i.d. observations from two populations with continuous distribution functions (d.f’s), from 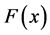 and
and 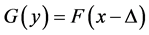 respectively, and consider the standard two-sample (non parametric) location problem of testing
respectively, and consider the standard two-sample (non parametric) location problem of testing 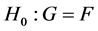 versus the alternatives
versus the alternatives 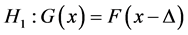 with
with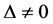 , for some unknown continuous d.f. F and a real (shift) parameter
, for some unknown continuous d.f. F and a real (shift) parameter . In the above testing problem we may also consider one sided say, right sided alternatives
. In the above testing problem we may also consider one sided say, right sided alternatives . In this paper, we proposed a class of tests for two-sample location problem based subsample quantiles and investigated the properties such as asymptotic normality, asymptotic efficiencies etc.
. In this paper, we proposed a class of tests for two-sample location problem based subsample quantiles and investigated the properties such as asymptotic normality, asymptotic efficiencies etc.
2. Materials and Methods
The study here is intended to propose new class of tests for two-sample location problem and study the properties of the test statistics. The performance of few members of the class of test statistics is also studied.
The Proposed Class of Tests
Let 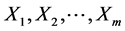 and
and 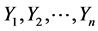 be two independent random samples of i.i.d. observations from two populations with continuous distribution functions (d.f’s), from
be two independent random samples of i.i.d. observations from two populations with continuous distribution functions (d.f’s), from 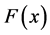 and
and 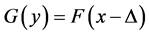 respectively. Consider the problem, of testing is to test the null hypothesis
respectively. Consider the problem, of testing is to test the null hypothesis 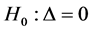 and
and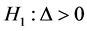 . Let c and d be any fixed positive integers such that
. Let c and d be any fixed positive integers such that 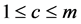 and
and 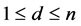 with
with 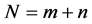 and consider all possible subsample of sizes c and d from
and consider all possible subsample of sizes c and d from 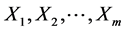 and
and 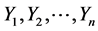 respectively. Based on the subsample, define kernel
respectively. Based on the subsample, define kernel
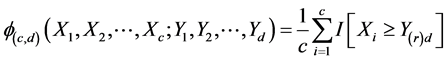 where
where  smallest among
smallest among 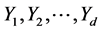 and
and .
.
Then, the U-statistics based on h1 is
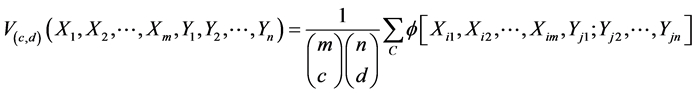
where C is the set of all possible integers 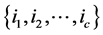 taken out of the set
taken out of the set 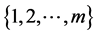 without replacement and all possible integers
without replacement and all possible integers 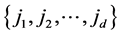 taken out of the set
taken out of the set 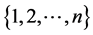 without replacement.
without replacement.
Asymptotic Distribution of the class of tests: Next we consider the asymptotic distribution of the test statistic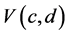 . For that we consider the expectation of
. For that we consider the expectation of  is
is
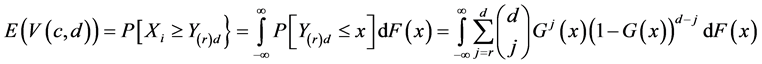
Under H0,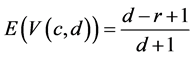 .
.
From the generalized U-statistics theorem due to Lehman (1951), it follows that the limiting distribution of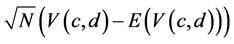 , as
, as 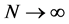 in such a way that
in such a way that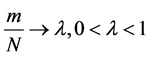 , is normal with mean zero and variance
, is normal with mean zero and variance

where
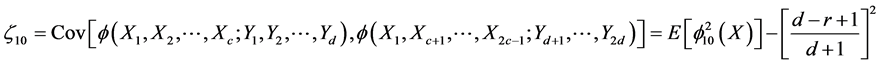
and
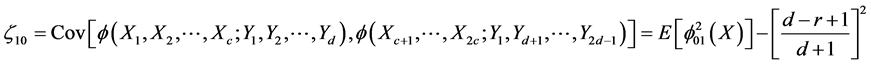
Now,
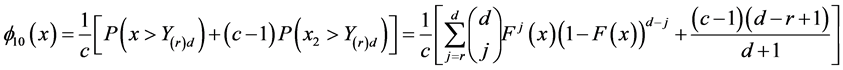
and
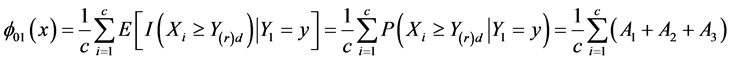
where
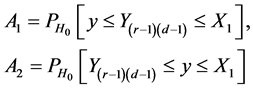 and
and
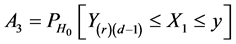 .
.
3. Results and Discussions
Pitman defined the asymptotic relative efficiency of one test S relative to another test T as the limiting ratio of sample sizes required to obtain the same limiting power for a sequence of alternatives converging to null hypothesis. By Noether’s theorem it follows that
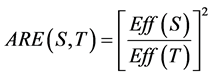 where
where
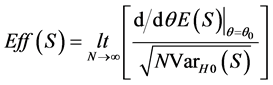 .
.
For asymptotic relative efficiency comparisons, two members of the class, 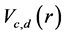 , namely,
, namely, 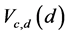 and
and 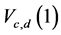 are considered.
are considered.
The mean of 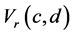 under
under 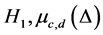 is given by
is given by

Then,
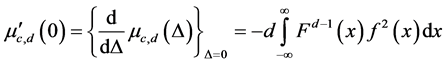
The ARE’s of 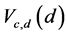 and
and 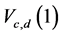 relative to the test due to a member of Xie and Priebe [9], which has maximum efficiency are computed for various distributions, namely, Cauchy, Laplace, Logistic, Normal, Uniform and Exponential distributions.
relative to the test due to a member of Xie and Priebe [9], which has maximum efficiency are computed for various distributions, namely, Cauchy, Laplace, Logistic, Normal, Uniform and Exponential distributions.
We present ARE’s of 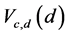 and
and 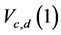 for various values of c, d in the Tables 1 and 2 respectively with respect to GMWW of Xie and Priebe [9].
for various values of c, d in the Tables 1 and 2 respectively with respect to GMWW of Xie and Priebe [9].
4. Conclusions
From the results and discussion section, we conclude as below:

Table 1. The ARE’s 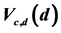 of various distributions w. r. to GMWW, when
of various distributions w. r. to GMWW, when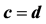 .
.

Table 2. The ARE’s 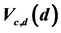 of various distributions w. r. to GMWW, when
of various distributions w. r. to GMWW, when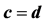 .
.
1) From the above investigation, we observe that for Cauchy, Logistic, uniform distribution and exponential distribution, the performance of the newly proposed test is better than the GMWW-test when 2 ≤ c = d ≤ 10.
2) The performance of the new test is better as compared to GMWW-test for Normal distribution, Power distribution (a = 2) and Power distribution (a = 3) when c = d and c = 2, 3, …, 10.
3) We also observed that for Normal distribution and uniform distribution, the performance of the newly proposed test 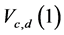 increases with d for fixed c and is better than the GMWW-test for c = 2 when 3 ≤ d ≤ 10.
increases with d for fixed c and is better than the GMWW-test for c = 2 when 3 ≤ d ≤ 10.
4) However, the performance of new test is better than GMWW-test for Normal and uniform distribution c ≤ d ≤ 10, and c = 3, 4, …, 10.
5) For Laplace distribution, the performance of the newly proposed test 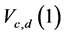 is better than the GMWWtest when c ≤ d ≤ 10 and c = 3, 4, 5. However, for Cauchy distribution, Laplace distribution and exponential distribution the newly proposed class of tests is not better than the GMWW-test for all values of c and d.
is better than the GMWWtest when c ≤ d ≤ 10 and c = 3, 4, 5. However, for Cauchy distribution, Laplace distribution and exponential distribution the newly proposed class of tests is not better than the GMWW-test for all values of c and d.
Acknowledgements
Authors thank the editor and the reviewers for their useful comments. The first author thank the UGC for its support through a grant F.No.41-807/2012(SR).
[2] J. Hajek and Z. Sidak, “Theory of Rank Tests,” Academic Press, New York, 1967.
[3] J. V. Deshpande and S. C. Kochar, “Some Competitors of Wilcoxon-Mann Whitney Test for the Location Alternatives,” Journal of Indian Statistical Association, Vol. 19, 1982, pp. 9-18.
[4] W. R. Stephenson and M. Gosh, “Two Sample Non-Parametric Tests Based on Subsamples,” Communications in Statistics— Theory and Methods, Vol. 14, No. 7, 1985, pp. 1669-1684. http://dx.doi.org/10.1080/03610928508829003
[5] E. L. Lehmann, “Consistency and Unbiasedness of Certain Nonparametric Tests,” Annals of Mathematical Statistics, Vol. 22, No. 2, 1951, pp. 165-179. http://dx.doi.org/10.1214/aoms/1177729639
[6] H. B. Mann and D. R. Whitney, “On a Test of Whether One of Two Random Variables Is Stochastically Larger than the Other,” Annals of Mathematical Statistics, Vol. 18, No. 1, 1947, pp. 50-60. http://dx.doi.org/10.1214/aoms/1177730491
[7] I. D. Shetty and Z. Govindarajulu, “A Two-Sample Test for Location,” Communications in Statistics—Theory and Methods, Vol. 17, No. 7, 1988, pp. 2389-2401. http://dx.doi.org/10.1080/03610928808829752
[8] I. D. Shetty and S. V. Bhat, “A Note on the Generalization of Mathisen’s Median Test,” Statistics & Probability Letters, Vol. 19, No. 3, 1994, pp. 199-204. http://dx.doi.org/10.1016/0167-7152(94)90105-8
[9] I. A. Ahmad, “A Class of Mann-Whitney-Wilcoxon Type Statistics,” The American Statistician, Vol. 50, No. 4, 1996, pp. 324-327.
[10] J. Xie and C. E. Priere, “Generalizing the Mann-Whitney Wilcoxon Statistic,” Journal of Non-Parametric Statistics, Vol. 12, No. 5, 2000, pp. 661-682. http://dx.doi.org/10.1080/10485250008832827