1. Introduction
Mixed monotone operators were introduced by Dajun Guo and V. Lakshmikantham in [1] in 1987. Thereafter, many authors have investigated these kinds of operators in Banach spaces and obtained a lot of interesting and important results. They are used extensively in nonlinear differential and integral equations. In this paper, without any compact and continuous assumption, we obtained some new existence and uniqueness theorems of positive fixed point of e-concave-convex mixed monotone operators in Banach spaces partially ordered by a cone.
Let the real Banach space 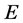 be partially ordered by a cone
be partially ordered by a cone 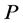 of
of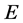 , i.e.,
, i.e.,  iff
iff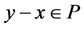 .
. 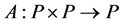 is said to be a mixed monotone operator if
is said to be a mixed monotone operator if 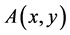 is increasing in
is increasing in 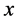 and decreasing in
and decreasing in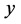 , i.e.,
, i.e., 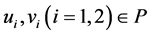 ,
, 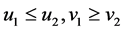 implies.
implies. . Element
. Element 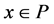 is called a fixed point of
is called a fixed point of 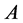 iff
iff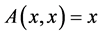 .
.
Recall that cone  is said to be solid if the interior
is said to be solid if the interior 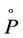 is nonempty and we denote
is nonempty and we denote  if
if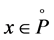 .
. 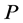 is normal if there exists a positive constant N, such that
is normal if there exists a positive constant N, such that 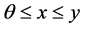 implies
implies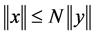 ,
, 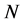 is called the normal constant of
is called the normal constant of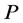 .
.
For all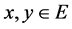 , the notation
, the notation  means that there exist
means that there exist 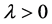 and
and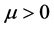 , such that
, such that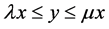 . Clearly,
. Clearly,  is an equivalence relation. Given
is an equivalence relation. Given , we denote by
, we denote by 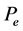 the set
the set . It is easy to see that
. It is easy to see that 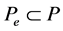 is convex and
is convex and  for all
for all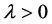 . If
. If 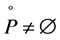 and
and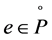 , it is clear that
, it is clear that .
.
All the concepts discussed above can be found in [2-4]. For more facts about mixed monotone operators and other related concepts, the reader could refer to [5-7] and some of the reference therein.
2. Main Results
In this section, we present our main results. To begin with, we give the definition of e-concave-convex operators.
Definition 2.1. We say an operator 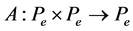 is an e-concave-convex operators if there exist one positive function
is an e-concave-convex operators if there exist one positive function  such that
such that
 (2.1)
(2.1)
Remark 2.1. (2.1) implies that
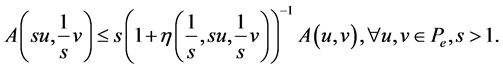 (2.2)
(2.2)
Theorem 2.1. Let 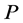 be a normal cone of
be a normal cone of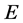 , and let
, and let 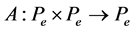 be a mixed monotone and e-concave-convex operator. In addition, suppose that there exist
be a mixed monotone and e-concave-convex operator. In addition, suppose that there exist 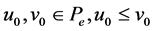 (Since
(Since , we can choose a sufficiently small
, we can choose a sufficiently small 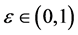 such that
such that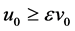 ) such that
) such that
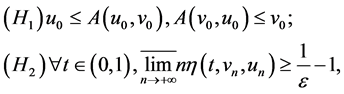
hold, where . Then
. Then 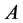 has exactly one fixed pint x* in
has exactly one fixed pint x* in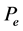 . Moreover, constructing successively the sequence
. Moreover, constructing successively the sequence
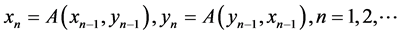 for any initial
for any initial , we have
, we have
 (2.3)
(2.3)
Proof. We divide the proof into 3 steps.
Step 1. We prove A has a fixed point in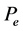 .
.
Construct successively the sequences
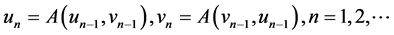 .
.
It follows from 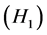 and the mixed monotonicity of
and the mixed monotonicity of 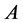 that
that
 . (2.4)
. (2.4)
Let
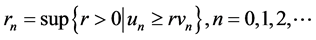 .
.
Thus we have , and then
, and then
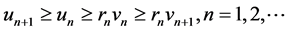 .
.
Therefore, 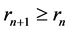 , i.e.,
, i.e., 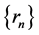 is increasing with
is increasing with .
.
Suppose 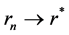 as
as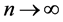 . Then
. Then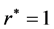 . Indeed, suppose to the contrary that
. Indeed, suppose to the contrary that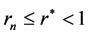 . By
. By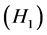 , (2.1) and the mixed monotonicity of
, (2.1) and the mixed monotonicity of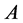 , we have
, we have
 .
.
Therefore
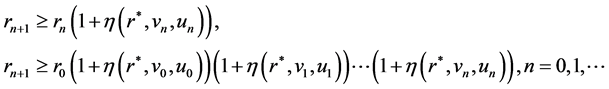 (2.5)
(2.5)
By (2.1) and the mixed monotonicity of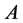 , we know that
, we know that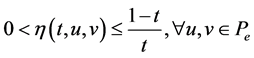 , and thus
, and thus
 exists. We distinguish two cases.
exists. We distinguish two cases.
Case 1: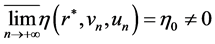 . In this case we know that
. In this case we know that  So, we have
So, we have
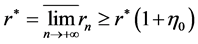 , which is a contradiction.
, which is a contradiction.
Case 2: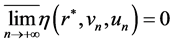 . In this case, it is easy to see that
. In this case, it is easy to see that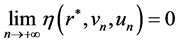 . For convenience’s sake, let
. For convenience’s sake, let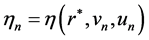 . Since
. Since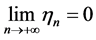 , there is a nonincreasing subsequence
, there is a nonincreasing subsequence 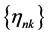 of
of 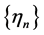 such that
such that
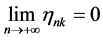 . Without loss of generality, we may still use
. Without loss of generality, we may still use 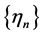 to stand for
to stand for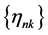 . From (2.5), we obtain
. From (2.5), we obtain
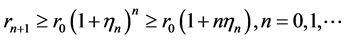 .
.
Hence
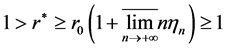 which is also a contradiction. Thus
which is also a contradiction. Thus .
.
For any natural number 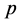 we have
we have
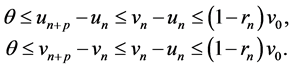
Since 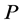 is normal, we have
is normal, we have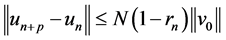 ,
,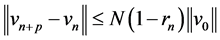 . Here N is the normality constant.
. Here N is the normality constant.
So 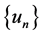 and
and 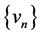 are Cauchy sequences. Because E is complete, there exist
are Cauchy sequences. Because E is complete, there exist  such that
such that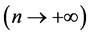
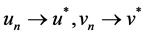 , By (2.4) we know that
, By (2.4) we know that  and
and
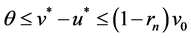 .
.
Further
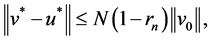
And thus . Let
. Let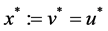 , we obtain
, we obtain

Let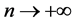 , we get
, we get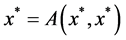 . That is, x* is a fixed point of
. That is, x* is a fixed point of 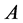 in
in .
.
Step 2. We prove that x* is the unique fixed point of  in
in .
.
In fact, suppose 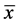 is another fixed point of
is another fixed point of 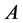 in
in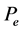 . Since
. Since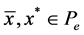 , there exist positive numbers
, there exist positive numbers 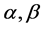 such that
such that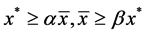 . Let
. Let
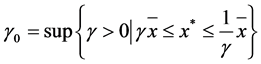 . (2.6)
. (2.6)
Evidently,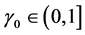 . We now prove
. We now prove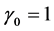 . If otherwise,
. If otherwise,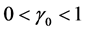 . From (2.1), we obtain
. From (2.1), we obtain

Which contradicts the definition of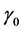 . Hence
. Hence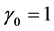 , thus
, thus . Therefore A has a unique fixed point x* in
. Therefore A has a unique fixed point x* in .
.
Step 3. We prove (2.3).
For any , we can choose a small number
, we can choose a small number 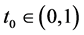 such that
such that
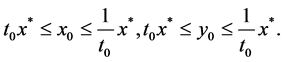 (2.7)
(2.7)
Let
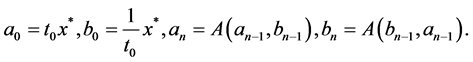 (2.8)
(2.8)
Using (2.7), (2.8) and the mixed monotonicity of A, we have
 (2.9)
(2.9)
Let
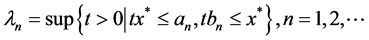 . (2.10)
. (2.10)
From (2.8) and (2.9), we obtain
 (2.11)
(2.11)
In what follows, we will prove that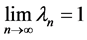 . If not, that is,
. If not, that is, 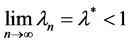 , then from (2.8) and (2.11), we have
, then from (2.8) and (2.11), we have
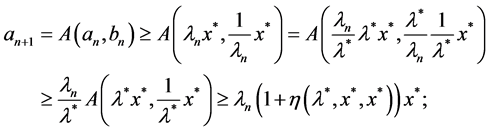 (2.12)
(2.12)
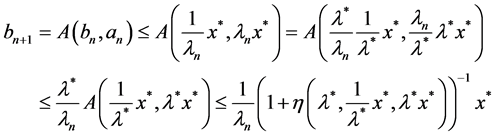 . (2.13)
. (2.13)
Let . It follows from (2.11), (2.12) and (2.13) that
. It follows from (2.11), (2.12) and (2.13) that
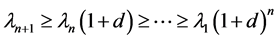 , which is a contradiction. That is
, which is a contradiction. That is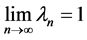 .
.
From (2.9) and (2.11), we have
 .
.
Thus,
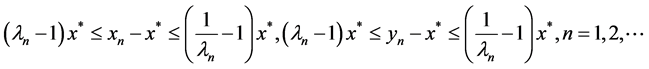 .
.
By using the normality of , we know that (2.2) holds.
, we know that (2.2) holds.
3. Concerned Remarks and Corollaries
Using Theorem 2.1, we have the following corollaries.
Corollary 3.1. Let P be a normal cone of E, and let 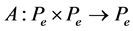 be a mixed monotone and e-concaveconvex operator. In addition, suppose that there exist
be a mixed monotone and e-concaveconvex operator. In addition, suppose that there exist 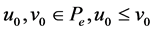 (Since
(Since , we can choose a sufficiently small
, we can choose a sufficiently small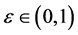 , such that
, such that ), such that
), such that
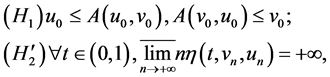
hold, where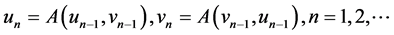 . Then A has exactly one fixed pint x* in
. Then A has exactly one fixed pint x* in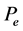 . Moreover, constructing successively the sequence
. Moreover, constructing successively the sequence
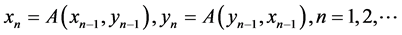 for any initial
for any initial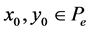 , we have
, we have
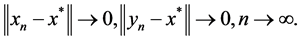
Corollary 3.2. Let P be a normal cone of E, and let 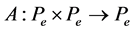 be a mixed monotone and e-concaveconvex operator. In addition, suppose that
be a mixed monotone and e-concaveconvex operator. In addition, suppose that
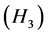 there exist
there exist 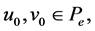 such that
such that 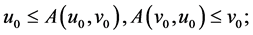
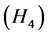 for all
for all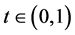 , there exist
, there exist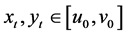 , such that
, such that 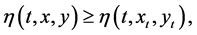
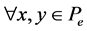 hold.
hold.
Then  has exactly one fixed pint
has exactly one fixed pint 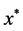 in
in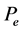 . Moreover, constructing successively the sequence
. Moreover, constructing successively the sequence
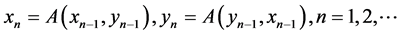 for any initial
for any initial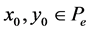 , we have
, we have
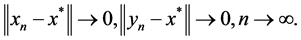
Corollary 3.3. Let P be a normal cone of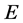 , and let
, and let  be a mixed monotone and e-concaveconvex operator. In addition, suppose that
be a mixed monotone and e-concaveconvex operator. In addition, suppose that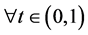 ,
, 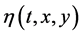 are monotone on
are monotone on 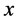 and
and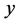 . Then a necessary and sufficient condition for
. Then a necessary and sufficient condition for 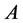 to have exactly one fixed pint
to have exactly one fixed pint 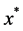 in
in  is that
is that 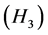 holds. Moreover, constructing successively the sequence
holds. Moreover, constructing successively the sequence
 for any initial
for any initial , we have
, we have
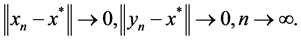
Proof. Corollary 3.1 ensures the sufficiency of Corollary 2.3, so we have only to prove the necessity of Corollary 2.3.
Suppose that x* is the unique fixed point of 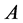 in
in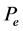 . For any
. For any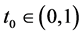 , let
, let
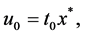 . It follows from (1.1), (1.2) and the mixed monotonicity of A that
. It follows from (1.1), (1.2) and the mixed monotonicity of A that
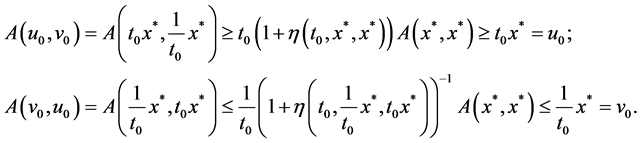
Therefore, 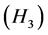 holds.
holds.
Corollary 3.4. Let 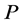 be a normal cone of
be a normal cone of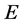 , and let
, and let 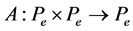 be a mixed monotone operator. In addition, suppose that
be a mixed monotone operator. In addition, suppose that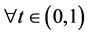 , there exists
, there exists 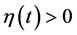 such that
such that
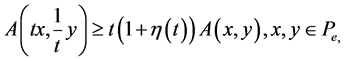 (3.1)
(3.1)
holds. Then a necessary and sufficient condition for  to have exactly one fixed pint
to have exactly one fixed pint 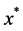 in
in 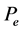 is that
is that  holds. Moreover, constructing successively the sequence
holds. Moreover, constructing successively the sequence
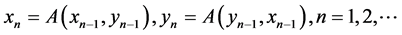 for any initial
for any initial , we have
, we have

Corollary 3.5. Let 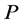 be a normal cone of
be a normal cone of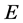 , and let
, and let 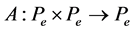 be a mixed monotone operator with property (2.1). In addition, suppose that
be a mixed monotone operator with property (2.1). In addition, suppose that 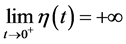 holds. Then
holds. Then 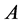 has exactly one fixed pint x* in
has exactly one fixed pint x* in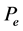 .
.
Proof. In fact, by corollary 2.4, we have only to prove that 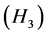 holds.
holds.
For any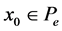 , it follows from
, it follows from 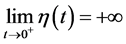 that there exists
that there exists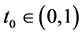 , such that
, such that
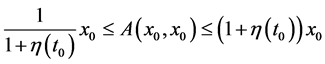 . Let
. Let . Following from (3.1) and the mixed monotonicity of A, we get
. Following from (3.1) and the mixed monotonicity of A, we get
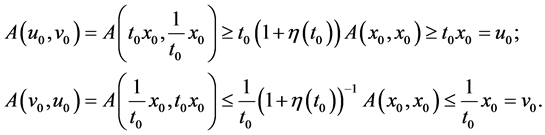
The Corollary 3.5 is thus proved.
Acknowledgements
The author thanks the referee for his valuable comments and suggestions. This paper was supported by SRFDP (NO. 20103705120002).