A Polynomial Algorithm of Optimum Cutting a Rectangle into Rectangles with Two Heights ()
Keywords: Cutting; Convex Hull; Polynomial Algorithms
1. Introduction
The problems of rectangular packing and cutting are difficult problems of discrete optimization (for references see [1]). For example, the computational complexity of the problem of packing in a rectangular sheet  the maximum number of equal small rectangles
the maximum number of equal small rectangles  (pallet loading problem (PLP)) is unknown. Fast polynomial algorithms [2,3] are known for the problem of optimally guillotine cutting a rectangle
(pallet loading problem (PLP)) is unknown. Fast polynomial algorithms [2,3] are known for the problem of optimally guillotine cutting a rectangle  into rectangles
into rectangles  where 90˚ rotations are allowed. In [4,5] the problem of guillotine cutting a rectangular sheet
where 90˚ rotations are allowed. In [4,5] the problem of guillotine cutting a rectangular sheet  into rectangles
into rectangles  with a minimal trim loss is considered and polynomial algorithms for its solution are presented for the case when the number of occurrences of small rectangles in a cutting pattern is not restricted and rectangles cannot be rotated. Adding a constraint on the number of occurrences of rectangles
with a minimal trim loss is considered and polynomial algorithms for its solution are presented for the case when the number of occurrences of small rectangles in a cutting pattern is not restricted and rectangles cannot be rotated. Adding a constraint on the number of occurrences of rectangles  complicates the problem. It is not known whether the problem of guillotine cutting a rectangular sheet
complicates the problem. It is not known whether the problem of guillotine cutting a rectangular sheet 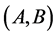 into
into 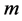 rectangles
rectangles  and
and 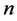 rectangles
rectangles  belongs to
belongs to 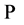 (the class of the problems which are solvable in polynomial time). The general problem of packing is strongly NP-hard, and in a guillotine case it has pseudopolynomial algorithm of dynamic programming. For integer variant of a problem, from polynomial algorithm of Lenstra [6] for a problem of integer linear programming, it follows a polynomial algorithm for optimum packing of rectangles
(the class of the problems which are solvable in polynomial time). The general problem of packing is strongly NP-hard, and in a guillotine case it has pseudopolynomial algorithm of dynamic programming. For integer variant of a problem, from polynomial algorithm of Lenstra [6] for a problem of integer linear programming, it follows a polynomial algorithm for optimum packing of rectangles 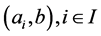 in a rectangle
in a rectangle 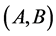 with the fixed set
with the fixed set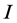 . When there are constraints on number of rectangles, the existence of polynomial algorithm is problematic. The matter is that the problem about optimum packing
. When there are constraints on number of rectangles, the existence of polynomial algorithm is problematic. The matter is that the problem about optimum packing 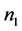 rectangles
rectangles ,
, 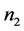 of rectangles
of rectangles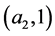 ,
,  of rectangles
of rectangles  into a rectangle
into a rectangle  is equivalent to a problem MSP3 (the problem of packing bins with three lengths), for which the existence of polynomial algorithm is an unsolved problem of the schedulling theory so far [7]. We consider the problem of optimum (i.e with the minimum trim lost) guillotine cutting a rectangle
is equivalent to a problem MSP3 (the problem of packing bins with three lengths), for which the existence of polynomial algorithm is an unsolved problem of the schedulling theory so far [7]. We consider the problem of optimum (i.e with the minimum trim lost) guillotine cutting a rectangle  into rectangles with two heights
into rectangles with two heights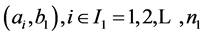 ,
, 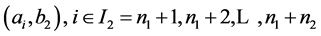 without restrictions on the number of copies of each rectangle. Let’s designate this problem
without restrictions on the number of copies of each rectangle. Let’s designate this problem
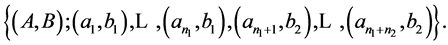
This paper is organized as follows: In Section 2, we consider the properties of a knapsack polygon (the convex hull of the set of feasible solutions of a 2-dimensional knapsack problem). Section 2 is auxiliary for Section 3 but it is self-interesting for the theory of knapsack problems. In Section 3, we prove the main results about the existence of polynomial algorithm for considered cutting problem.
2. Some Properties of a Knapsack Polygon
The set of feasible solutions of a knapsack problem plays an important role for problems of guillotine cutting. In a 2-dimensional case, this set is presented as:

where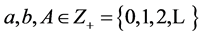 . The convex hull of this set refers to as a knapsack polygon denoted by
. The convex hull of this set refers to as a knapsack polygon denoted by
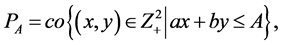
where co denote the convex hull operation.
Let’s show, that a knapsack polygon 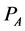 can be presented as
can be presented as
 (1)
(1)
where  is a right triangle with vertices
is a right triangle with vertices ,
,  is a number of nonzero vertices of
is a number of nonzero vertices of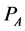 , the symbol
, the symbol  denotes an algebraic sum (the Minkowski sum) of sets:
denotes an algebraic sum (the Minkowski sum) of sets:
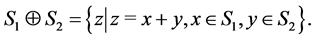
If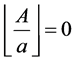 , then it is easy to see, that
, then it is easy to see, that
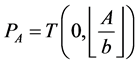
is a singular triangle—an interval, connecting points . Similarly, if
. Similarly, if , then
, then
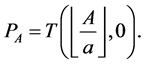
Let’s consider the case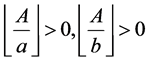 . Let nonzero vertices of
. Let nonzero vertices of  are sorted by increasing x-coordinates. Then the first vertex is
are sorted by increasing x-coordinates. Then the first vertex is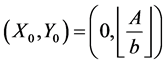 . Let
. Let  be the second nonzero vertex of
be the second nonzero vertex of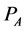 . Then
. Then

where  is defined as:
is defined as:

and all nonzero vertices of 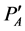 are translation of vertices of
are translation of vertices of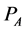 , excepting the first, by
, excepting the first, by . Applying an induction, we obtain required representation.
. Applying an induction, we obtain required representation.
Remark. This representation follows from a well-known representation of a convex polygon up to translation by the set of its sides sorted in counter-clockwise or clockwise order [8]. Note also that the Minkowski sum of two polygons can be presented by the union of their sides up to translation.
It is easy to establish the following recurrent equations, connecting coordinates of vertices and parameters of right triangles in the above representation:
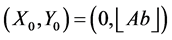
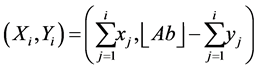

Note the following properties of this representation:
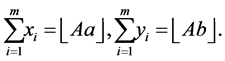
If triangles are sorted by increasing 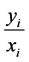 order, then only one triangle can be singular: the first
order, then only one triangle can be singular: the first  , if
, if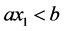 then
then , and the last
, and the last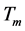 , if
, if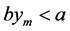 , then
, then . If in (1), where right triangles
. If in (1), where right triangles 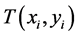 are sorted by increasing
are sorted by increasing  order, there are no singular triangles, then it is possible to add singular the first and last triangles
order, there are no singular triangles, then it is possible to add singular the first and last triangles
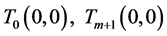 . Thus, from the beginning we may assume, that
. Thus, from the beginning we may assume, that 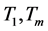 are singular triangles
are singular triangles 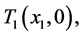
 .
.
Among other properties note the following property. If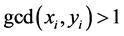 , then
, then
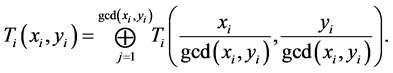
The similar possibility of further decomposition appears in the case, when boundary of a knapsack polygon besides vertices contains also other points of an integer lattice 
Consider an example of a knapsack polygon:
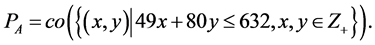
It has 6 non zero vertices (0,7), (1,7), (3,6), (8,3), (11,1), (12,0) and can be presented by the Minkowski sum of right triangles:

where  is a singular triangle.
is a singular triangle.
Remark. If we denote by  the set of integer points in
the set of integer points in :
:

then we have the next formula for the set of feasible solutions in a 2-dimensional knapsack problem:

where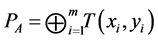 .
.
A knapsack polygon is characterized by a triplet of integer non-negative numbers .
.
Definition 1 A triplet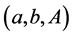 , describing a knapsack polygon, is equivalent to a triplet
, describing a knapsack polygon, is equivalent to a triplet 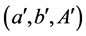
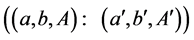 if the sets of feasible solutions of corresponding knapsack problems are equal:
if the sets of feasible solutions of corresponding knapsack problems are equal:
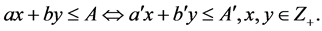
We say that a triplet 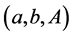 can be decreased, if there exists an equivalent triplet
can be decreased, if there exists an equivalent triplet 

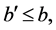
 , and
, and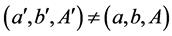 .
.
Neighboring Farey fractions of  [9]:
[9]:
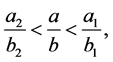

play an important role for a possibility of decreasing a triplet 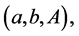
 .
.
It is easy to show, that if 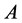 is replaced by the optimum value of a knapsack problem:
is replaced by the optimum value of a knapsack problem:

then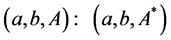 . If in addition,
. If in addition, 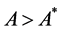 , then the triplet
, then the triplet  can be decreased. Thus, we can assume that
can be decreased. Thus, we can assume that 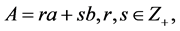
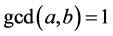 . If
. If 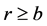 or
or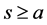 , then the triplet
, then the triplet 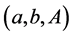 can not be decreased. Let’s show, that the triplet
can not be decreased. Let’s show, that the triplet 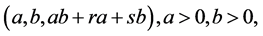
 can not be decreased. Suppose on the contrary that there exists a triplet
can not be decreased. Suppose on the contrary that there exists a triplet :
:
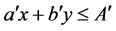 (2)
(2)
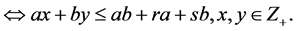 (3)
(3)
Because points
 they also belong to
they also belong to
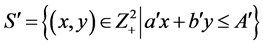 .
.
From here follows, that
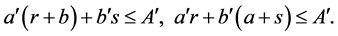
Let’s consider two cases: a) , b)
, b) .
.
a). Let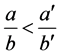 . By virtue of properties of Farey series
. By virtue of properties of Farey series

Consider a point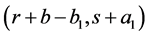 . It satisfies (2), because
. It satisfies (2), because

At the same time, this point does not satisfy (3):

That is, triplets 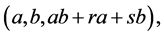
 are not equivalent.
are not equivalent.
b). Similarly, if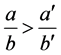 , then by the properties of Farey series
, then by the properties of Farey series

Consider a point . It satisfies (2), because
. It satisfies (2), because

On the other hand, it does not satisfy (3):

That is, in this case triplets 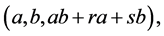
 are not equivalent too.
are not equivalent too.
Thus, a question about decreasing a triplet  is interesting only if
is interesting only if 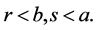
Lemma 1 Let be given a knapsack problem, the set of feasible solutions of which is given by an inequality

The triplet  c an not be decreased if and only if
c an not be decreased if and only if 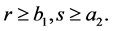
Proof. We prove this lemma by contradiction. Let, for example, . We shall show, that the triplet
. We shall show, that the triplet  can be decreased. Let’s show, that the following inequalities
can be decreased. Let’s show, that the following inequalities
 (4)
(4)
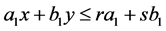 (5)
(5)
are equivalent.
1) Let . Let’s show, that
. Let’s show, that
 .
.
Inequality (4) is equivalent to . Consider three cases: a)
. Consider three cases: a) , b)
, b) , c)
, c) .
.
a). If , then
, then 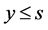 and
and .
.
b). If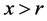 , then
, then . Because
. Because , then
, then . By the properties of Farey series, in interval
. By the properties of Farey series, in interval 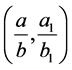 there are no numbers with denominator smaller than
there are no numbers with denominator smaller than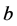 , therefore
, therefore , i.e.,
, i.e., .
.
c). Let . Then
. Then . Especially,
. Especially, . That is
. That is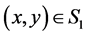 .
.
2) Let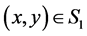 . We shall show, that
. We shall show, that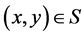 . Inequality (5) can be rewritten as
. Inequality (5) can be rewritten as . Consider three cases: a)
. Consider three cases: a) , b)
, b)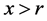 , c)
, c) .
.
a). If , then
, then . From here follows, that
. From here follows, that .
.
b). Let . Then
. Then . Especially,
. Especially,  , i.e.,
, i.e.,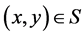 .
.
c). Let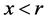 . Then
. Then  and
and . Because an interval
. Because an interval  does not contain rational numbers with a denominator smaller than
does not contain rational numbers with a denominator smaller than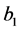 ,
, 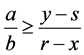 , i.e.,
, i.e., .
.
The equivalence of Inequalities (4) and (5) shows a possibility of decreasing the parameters of Inequality (4) if .
.
A possibility of decreasing the parameters of Inequality (4) if 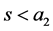 can be shown similarly.
can be shown similarly.
Let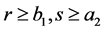 . We shall show, that it is impossible to decrease parameters. Let, on the contrary, the triplet
. We shall show, that it is impossible to decrease parameters. Let, on the contrary, the triplet 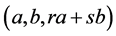 can be decreased. Then there is a triplet
can be decreased. Then there is a triplet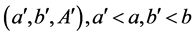 :
:
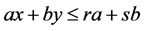 (6)
(6)
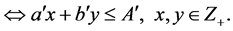 (7)
(7)
First of all,  , as
, as 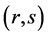 is a solution of (6), (7). Consider two possible cases: a)
is a solution of (6), (7). Consider two possible cases: a)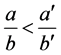 , b)
, b)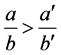 .
.
a). Let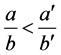 . By the property of numbers of Farey series
. By the property of numbers of Farey series

But the point 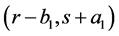 does not satisfy (6) because
does not satisfy (6) because
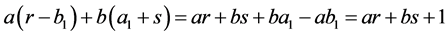
and satisfies (7) because  and
and
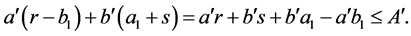
That is, in this case decreasing of parameters is impossible.
b) Let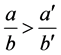 . By the property of numbers of Farey series
. By the property of numbers of Farey series

and 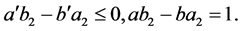 Take a point
Take a point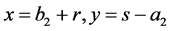 . Then (7) is carried out:
. Then (7) is carried out:

At the same time, (6) is not carried out because
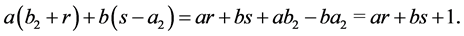
The lemma is proved.
3. Main Results
It appears that considered problem of optimum guillotine cutting can be decomposed into two subproblems. The following theorem is valid.
Theorem 1 Let . Then among optimum cuttings of a problem
. Then among optimum cuttings of a problem

there exists cutting the side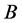 , such that we have the reduction of an initial problem to two subproblems
, such that we have the reduction of an initial problem to two subproblems
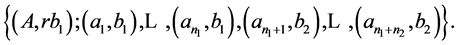
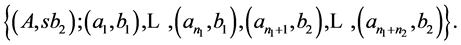
Proof. Let’s prove the theorem by contradiction. Let 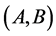 be a rectangle of the minimal area, for which the theorem is not correct. If the first cut for optimum cutting divides the side
be a rectangle of the minimal area, for which the theorem is not correct. If the first cut for optimum cutting divides the side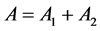 , the theorem will be fair for rectangles
, the theorem will be fair for rectangles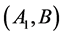 ,
,  and for both of them the first cut divides the side
and for both of them the first cut divides the side . Let the first cut divides the side
. Let the first cut divides the side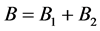 . Replace
. Replace 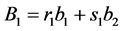 ,
, . If
. If 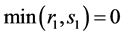 or
or , the contradiction easily follows from the reasons, that for rectangles
, the contradiction easily follows from the reasons, that for rectangles ,
, 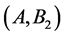 the theorem is valid. Let, for example,
the theorem is valid. Let, for example,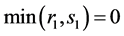 . Then
. Then 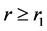 or
or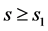 . If
. If , we have the first cut
, we have the first cut 
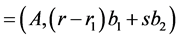 and according to the theorem the second rectangle is cut into rectangles
and according to the theorem the second rectangle is cut into rectangles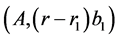 ,
,
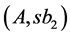 . By glueing together rectangles
. By glueing together rectangles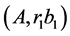 ,
,  we can receive optimum cut
we can receive optimum cut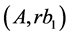 ,
,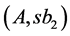 . Thus, the desired contradiction can be received only if
. Thus, the desired contradiction can be received only if . If
. If , or
, or , the contradiction again can be received easily. Really, let we have the first cut
, the contradiction again can be received easily. Really, let we have the first cut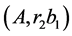 ,
, . Because
. Because , then
, then  or
or . Let the optimum cut is
. Let the optimum cut is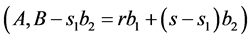 ,
,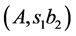 . Then according to the theorem we have the cut
. Then according to the theorem we have the cut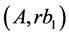 ,
,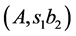
 . By sticking together the second and third rectangles we have the optimum cut
. By sticking together the second and third rectangles we have the optimum cut ,
,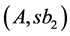 . It is necessary to consider the case
. It is necessary to consider the case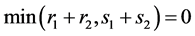 . Let, for example,
. Let, for example, . That is, the optimum cutting has a form
. That is, the optimum cutting has a form ,
,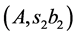 . If
. If  and
and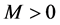 , then
, then 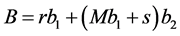 and
and , as
, as  and it is easy to receive the contradiction. Let, for example,
and it is easy to receive the contradiction. Let, for example, . For a rectangle
. For a rectangle 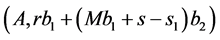 the theorem is validtherefore we have cutting into rectangles
the theorem is validtherefore we have cutting into rectangles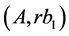 ,
,  ,
,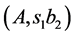 . It is possible to glue this cutting together with the cutting
. It is possible to glue this cutting together with the cutting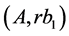 ,
,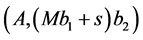 . That is, the contradiction results to
. That is, the contradiction results to . If it is possible to reduce the triplet
. If it is possible to reduce the triplet 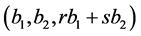 to the triplet
to the triplet , by means of the theorem of equivalence [3] then the cutting for a rectangle
, by means of the theorem of equivalence [3] then the cutting for a rectangle  is decomposed, but then the cutting for a rectangle
is decomposed, but then the cutting for a rectangle  is decomposed into rectangles
is decomposed into rectangles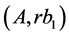 ,
, 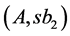 too. Therefore, the triplet
too. Therefore, the triplet 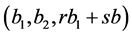 cannot be reduced and from the lemma 1 we have
cannot be reduced and from the lemma 1 we have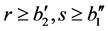 , where
, where

are three consecutive members of the Farey series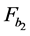 . That is, we have optimum cutting into rectangles
. That is, we have optimum cutting into rectangles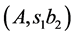 ,
,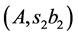 . But cutting into rectangles
. But cutting into rectangles ,
, 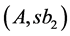 will not be optimum. Because
will not be optimum. Because 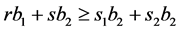 and the equality is not valid as
and the equality is not valid as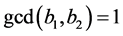 , that is
, that is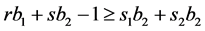 . Let’s consider rectangle
. Let’s consider rectangle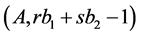 . If
. If 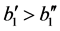 (and therefore
(and therefore ), we shall receive cutting into
), we shall receive cutting into  by presenting
by presenting 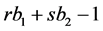 as
as . Because
. Because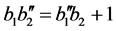 , we have cutting
, we have cutting . Then by gluing together first two rectangles we have required optimum cutting
. Then by gluing together first two rectangles we have required optimum cutting ,
,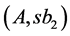 . The case
. The case 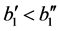 is considered similarly. The theorem is proved.
is considered similarly. The theorem is proved.
Now the polynomial algorithm for a considered rectangular cutting problem follows from the following reasons. Let’s consider the set of feasible solutions for the side 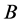

The convex hull of this set can be presented as the algebraic sum (Minkowski sum) of elementary triangles
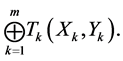
Application of the proved theorem and a the theorem 1 of equivalence [3] reduces the initial problem of optimum cutting to the set of problems of optimum cutting the rectangles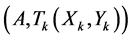 .
.
The next lemma follows from area estimations.
Lemma 2 Optimum cutting of a rectangle 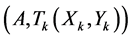 can be reduced to the decision of the following knapsack problem
can be reduced to the decision of the following knapsack problem
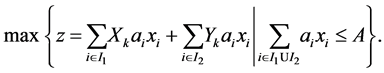 (8)
(8)
Proof. The proof is standard and can be omitted.
Knapsack problem (8) in the case of fixed sets 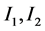 can be solved by the well known polynomial algorithm of Lenstra [6] for integer linear programming. Therefore, next lemma is valid.
can be solved by the well known polynomial algorithm of Lenstra [6] for integer linear programming. Therefore, next lemma is valid.
Lemma 3 For a problem of cutting 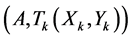 into rectangles
into rectangles 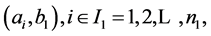
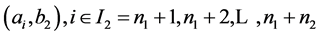 , with the fixed sets of indexes
, with the fixed sets of indexes  there exists a polynomial algorithm of optimum cutting.
there exists a polynomial algorithm of optimum cutting.
Proof. If the first cut divide the side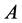 , i.e. we have cutting
, i.e. we have cutting ,
, 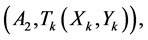
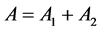 , then by applying an induction one would receive, that for
, then by applying an induction one would receive, that for ,
,  the lemma is valid and consequently the validity of the lemma for
the lemma is valid and consequently the validity of the lemma for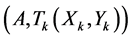 . Let the first cut divides
. Let the first cut divides . Then we have cutting into two rectangles
. Then we have cutting into two rectangles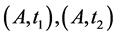 . But then by presenting the side
. But then by presenting the side  as the Minkowski sum of elementary triangles we can transform this cutting into cutting with the first cut dividing the side
as the Minkowski sum of elementary triangles we can transform this cutting into cutting with the first cut dividing the side . The lemma is proved.
. The lemma is proved.
Uniting all results we obtain the following theorem.
Theorem 2 For a problem of optimum cutting 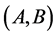 into rectangles
into rectangles 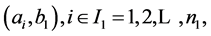
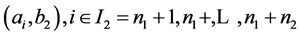 , with the fixed sets of indexes
, with the fixed sets of indexes  there exists a polynomial algorithm.
there exists a polynomial algorithm.
4. Conclusion
As it is said in introduction, the problems of guillotine rectangular cutting belong to the set of problems with pseudopolynomial algorithms. Intuition makes the hypothesis of existence of polynomial algorithm for the problem of optimum guillotine cutting into fixed number of small rectangles probable. In this paper, this hypothesis is justified for the problem of guillotine cutting a rectangular sheet into rectangular pieces with two heights.
[2] H. Dyckhoff, “A Typology of Cutting and Packing Problems,” European Journal of Operational Research, Vol. 44, No. 2, 1990, pp. 145-159. http://dx.doi.org/10.1016/0377-2217(90)90350-K
[3] A. G. Tarnowski, J. Terno and G. Scheithauer, “A Polynomial Time Algorithm for the Guillotine Pallet Loading Problem,” INFOR, Vol. 32, 1994, pp. 275-287.
[4] M. Z. Arslanov, “A Polynomial Algorithm for One Problem of Guillotine Cutting,” Operations Research Letters, Vol. 35, No. 5, 2007, pp. 636-644. http://dx.doi.org/10.1016/j.orl.2006.12.003
[5] A. G. Tarnowski, “Advanced Polynomial Time Algorithm for Guillotine Generalized Pallet Loading Problem,” In: The International Scientific Collection: Decision Making under Conditions of Uncertainty (Cutting-Packing Problems), Ufa State Aviation Technical University, 1997, pp. 93-124.
[6] E. Girlich and A. G. Tarnowski, “On Polynomial Solvability of Two Multiprocessor Scheduling Problems,” Mathematical Methods of Operations Research, Vol. 50, No. 1, 1999, pp. 27-51.
[7] H. W. Lenstra Jr., “Integer Programming with a Fixed Number of Variables,” Mathematics of Operations Research, Vol. 8, No. 4, 1983, pp. 538-548.
[8] S. T. McCormick, S. R. Smallwood and F. C. R. Spieksma, “A Polynomial Algorithm for Multiprocessor Scheduling with Two Job Lengths,” Mathematics of Operations Research, Vol. 26, No. 1, 2001, pp. 31-49.
[9] L. A. Lyusternik, “Convex Figures and Polyhedra,” Dover Publications, New York, 1963.
[10] R. K. Guy, “The Book of Numbers,” Springer-Verlag, New York, 1996.