Keywords: Heat Conduction; Inclusions; Defect; Heterogeneous Medium; Inverse Problem
1. Introduction
Under analysis is a nonclassical problem on heat conduction, with the known body’s surface temperature and surface heat flow. It is assumed that the medium is heterogeneous and contains inclusions. Coefficients of heat conductivity of the medium and inclusions are assumed by constants and differ among themselves. The problem is formulated as the problem on finding heterogeneities (flaw detection problem) by overdetermined surface conditions. On the boundary surface, the condition of continuity of the temperature and heat flow is fulfilled. Such problems belong to the nonclassical problems of mathematical physics.
Stationary problems of heat conduction are described by Equation , where
, where  is the temperature of a body and
is the temperature of a body and  is the Laplace operator. On an interface of two mediums conditions are satisfied
is the Laplace operator. On an interface of two mediums conditions are satisfied
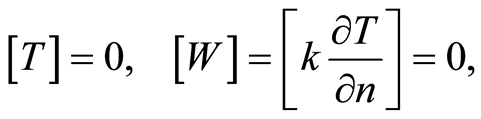 (1)
(1)
where 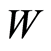 is the heat flow;
is the heat flow;  is the coefficient of the thermal conductivity.
is the coefficient of the thermal conductivity.
Hereinafter  is the coefficient of the host medium. It follows from (1) that the normal derivative of
is the coefficient of the host medium. It follows from (1) that the normal derivative of  becomes discontinuous at the boundary of two surface.
becomes discontinuous at the boundary of two surface.
Essentially overdefined condition for the Laplace equation mean assignment of values of  and
and  on
on , or, in our case, the values of
, or, in our case, the values of  and
and 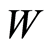 on
on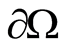 .
.
For a homogeneous medium, evidently, the essentially overdetermined conditions cannot be arbitrary, i.e.,  and
and 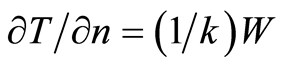 are functionally connected on
are functionally connected on . Let’s receive conditions of coordination for the last and consequences following from them.
. Let’s receive conditions of coordination for the last and consequences following from them.
Consider a body with volume  and surface
and surface . Let the functions
. Let the functions
 (2)
(2)
be potentials of the simple layer and double layer, respectively. Here,  is the fundamental solution of the Laplace equation [1];
is the fundamental solution of the Laplace equation [1];  and
and  are the densities of the layers, and n is a vector of external normal to
are the densities of the layers, and n is a vector of external normal to . It is assumed that
. It is assumed that  is piecewise-smooth according to Lyapunov and
is piecewise-smooth according to Lyapunov and 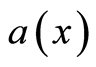 and
and  fulfill the Holder condition. Let
fulfill the Holder condition. Let , then
, then
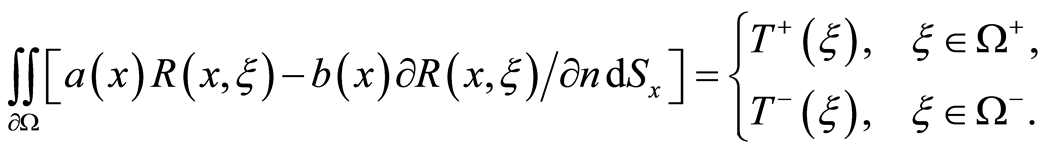 (3)
(3)
Here,  and
and  are, respectively, the exterior and interior of
are, respectively, the exterior and interior of , the boundary surface not included. It is stated that the densities
, the boundary surface not included. It is stated that the densities 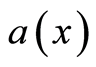 and
and  are concordant if
are concordant if  is continuous in
is continuous in  and is equal to
and is equal to 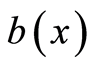 on
on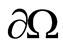 . The consistency of the densities can be interpreted as correspondence of
. The consistency of the densities can be interpreted as correspondence of  and
and  to the values of a harmonic potential
to the values of a harmonic potential 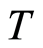 and its normal derivative on
and its normal derivative on 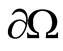 in the homogeneous medium. By the uniqueness of the Dirichlet and Neumann problem, the use of the densities
in the homogeneous medium. By the uniqueness of the Dirichlet and Neumann problem, the use of the densities 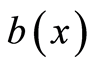 and
and  unequivocally recovers the concordant
unequivocally recovers the concordant 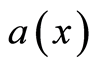 and
and , respectively. Hereinafter, the set
, respectively. Hereinafter, the set  of the concordant densities is denoted in terms of the class
of the concordant densities is denoted in terms of the class .
.
Statement 1. The densities b and a are concordant, i.e.  when and only when the equality below holds true
when and only when the equality below holds true
 (4)
(4)
where
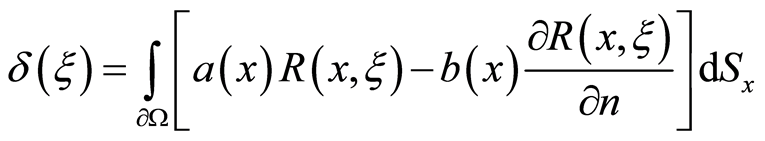 .
.
Proof. The necessity follows apparently from Green’s formula for harmonic functions [1]. Proving of the sufficiency uses equivalent of Sokhotsky-Plemeli’s formula
 (5)
(5)
where , and
, and  and
and  are the internal and external limit points relative to
are the internal and external limit points relative to , respectively. It follows from (4) that
, respectively. It follows from (4) that  from whence, considering (5), appears
from whence, considering (5), appears 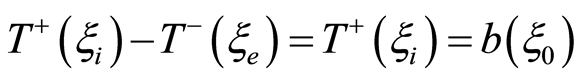 which is to be proved.
which is to be proved.
Statement 1 is similar to the theorem on boundary values of analytic function in the complex-variable function theory where conditions of continuous extension of analytical function from the closed contour to a domain are defined.
It is worth pointing at one property of the functions belonging to the class . Let
. Let  and
and  and
and  be the values of densities, found from (3), at the boundary of an area on
be the values of densities, found from (3), at the boundary of an area on ; then
; then . In addition, the condition of the Neumann problem resolvability is fulfilled at
. In addition, the condition of the Neumann problem resolvability is fulfilled at  and
and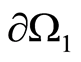 , which means that the heat flows through
, which means that the heat flows through  and
and  are zero.
are zero.
Subsequently, the potentials  and the flow
and the flow 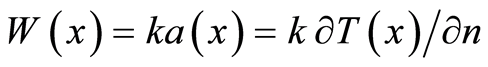 on
on  are assumed known. Then, the concordance conditions (4) are written as
are assumed known. Then, the concordance conditions (4) are written as  For
For , we also use
, we also use .
.
Let’s prove the statement following from the statement 1.
Statement 2. Let on the boundary  of the domain
of the domain 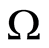 with the coefficient of the thermal conductivity coefficient
with the coefficient of the thermal conductivity coefficient  the temperature
the temperature 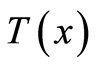 and the heat flow
and the heat flow 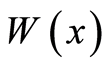 (
(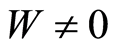 on
on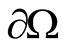 ) be assigned such that
) be assigned such that  Then
Then 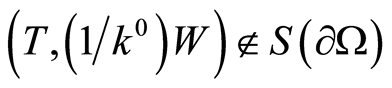 for any
for any  it has to be executed.
it has to be executed.
Proof. On  a function
a function  is introduced such that
is introduced such that  and
and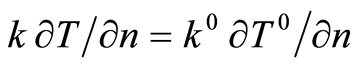 . Assume, that
. Assume, that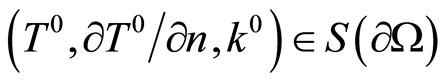 , i.e., in accord with (4)
, i.e., in accord with (4)
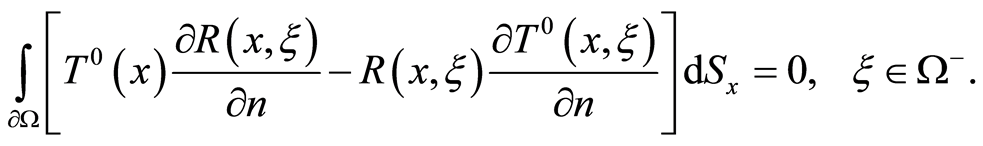 . (6)
. (6)
In the same way, from the condition  we have
we have
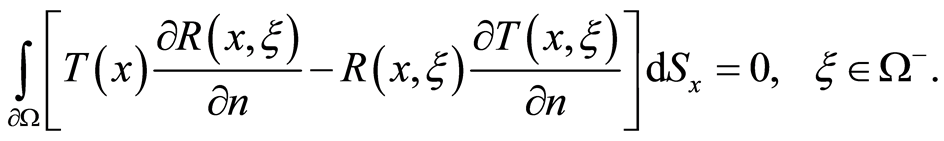 (7)
(7)
The flow condition  on
on  yields
yields
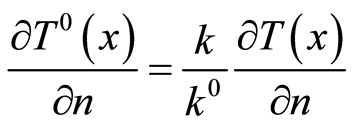 .
.
Placing the expression above in (6) and, then, its deduction from (7), considering 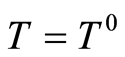 on
on , produces
, produces
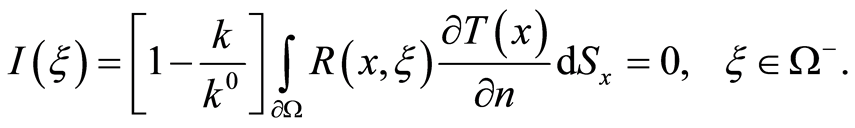
For the simple layer potential , it appears that the external normal derivative
, it appears that the external normal derivative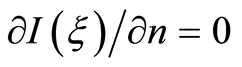 . Then, according to [1]
. Then, according to [1]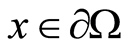
 , i.e. we come to a contradiction with a condition the statement. That is to say, the statement has been proved.
, i.e. we come to a contradiction with a condition the statement. That is to say, the statement has been proved.
Statement 3 (The theoremof the coefficient problem uniqueness). Let  and
and 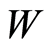 be assigned on
be assigned on 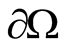 (
( on
on ). Then
). Then 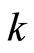 of the medium is uniquely found from the condition
of the medium is uniquely found from the condition .
.
Proof. Inasmuch as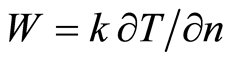 , the uniform medium concordance condition (4) can be written as
, the uniform medium concordance condition (4) can be written as
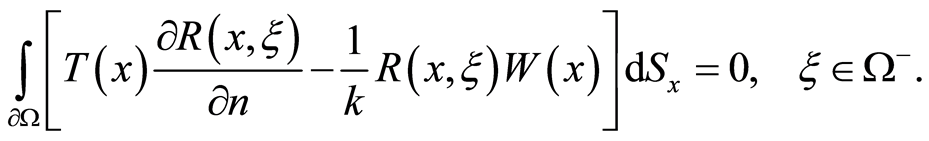 (8)
(8)
Let there exist  for which the condition (8) holds true, too. Rewrite (8) for
for which the condition (8) holds true, too. Rewrite (8) for  and diminish then (8) by
and diminish then (8) by
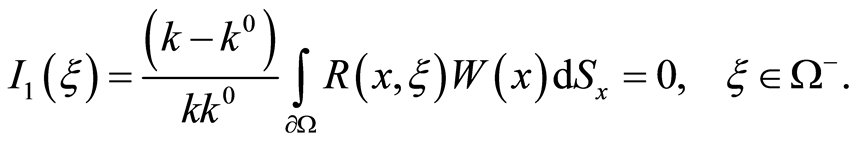
For the simple layer potential , it appears that the external normal derivative
, it appears that the external normal derivative . Then, according to [1],
. Then, according to [1], 
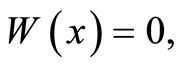 , i.e. we come to a contradiction with a condition the statement. That is to say, the statement has been proved.
, i.e. we come to a contradiction with a condition the statement. That is to say, the statement has been proved.
Consequence 1. If  and
and 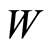
 are assigned on
are assigned on  and
and  and
and 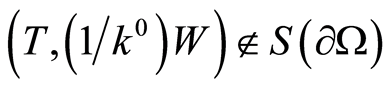 hold true, then
hold true, then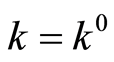 .
.
The condition (8) produces the formula for the coefficient of the thermal conductivity coefficient
 .
.
Let's notice that in [3] conditions for determination of the thermal conductivity coefficient for a non-stationary problem of heat conductivity are received.
Based on the introduced definitions and statements, there are a few inferences for a heterogeneous medium. A heterogeneous medium is understood to be the medium containing inclusions (defects), with the conjugacy condition (1) satisfied at their boundaries. Solving the problem on an extent from 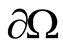 to an inclusion boundary
to an inclusion boundary  defines T and
defines T and  on.
on.  . The problem on the extent from
. The problem on the extent from  belongs to the known problems on the harmonic extension, i.e., Cauchy problem for the Laplace equation [2]. These problems belong to conditionally correct problems of mathematical physics and have the unique solution. Geophysics has many methods of solving such problems. One of methods is offered in [3-6].
belongs to the known problems on the harmonic extension, i.e., Cauchy problem for the Laplace equation [2]. These problems belong to conditionally correct problems of mathematical physics and have the unique solution. Geophysics has many methods of solving such problems. One of methods is offered in [3-6].
It is assumed that the condition 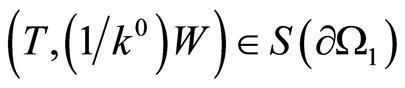 is fulfilled on the boundary
is fulfilled on the boundary  of the inclusion with
of the inclusion with . This condition is assumed to be the condition for the inclusion, which means continuity of the solution inside the inclusion, i.e., the inclusion is considered as a homogenous medium. Let us prove the following statement.
. This condition is assumed to be the condition for the inclusion, which means continuity of the solution inside the inclusion, i.e., the inclusion is considered as a homogenous medium. Let us prove the following statement.
Statement 4 (condition of existence of defect in a body). Let  and
and  be assigned on
be assigned on 
 . If the body contains an inclusion
. If the body contains an inclusion  with the thermal conductivity coefficient
with the thermal conductivity coefficient  (
( is the coefficient of the thermal conductivity coefficient of the host medium), then
is the coefficient of the thermal conductivity coefficient of the host medium), then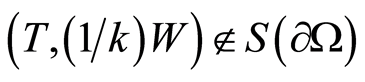 .
.
Proof. Assume . Continuing the decision from
. Continuing the decision from  to
to  on
on  we will find T,
we will find T,  and, consequently,
and, consequently, . According to the above mentioned property of
. According to the above mentioned property of  on
on , the condition
, the condition 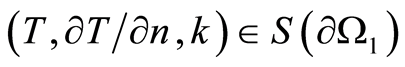 or, which is the same kind of thing,
or, which is the same kind of thing, 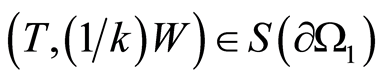 is to be fulfilled. On the other hand, the solution in the inclusion is continuous, i.e.
is to be fulfilled. On the other hand, the solution in the inclusion is continuous, i.e. . Thus, we have that
. Thus, we have that  and
and 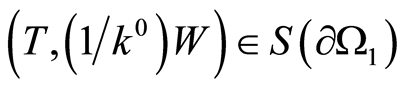 on
on . Under consequence 1, this is only possible when
. Under consequence 1, this is only possible when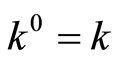 , which is a contradiction a statement condition. So, the statement has been proved.
, which is a contradiction a statement condition. So, the statement has been proved.
As follows from Statement 4, an inclusion as though initiates features of a field ; this means that in construction of the solution in
; this means that in construction of the solution in 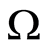 via the extent from
via the extent from , the potential is not expressed in terms of finite functions.
, the potential is not expressed in terms of finite functions.
The introduced definitions and proved statements allow stating the uniqueness of finding the inclusion boundary and the heat conductivity coefficient under fulfillment of the conjugacy condition (1).
Statement 5 (Theorem of the unique definition of inclusion boundary). Let in the medium  with
with ,
, 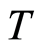 and
and  on
on  be known (
be known ( on
on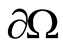 ) and let
) and let  contain an inclusion
contain an inclusion  with
with 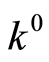
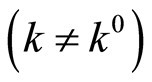 . Let the solution of the problem on the extent from
. Let the solution of the problem on the extent from  to
to , i.e. define
, i.e. define  and
and 
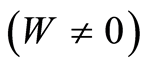 on
on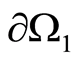 . Then the condition
. Then the condition  uniquely defines the boundary of the inclusion
uniquely defines the boundary of the inclusion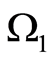 .
.
Proof. We extent the solution from  in
in . Let there be two surfaces
. Let there be two surfaces  and
and  in
in , and
, and  and
and  hold true at these surfaces. Below we consider three cases.
hold true at these surfaces. Below we consider three cases.
1) Let , Figure 1. Assign an arbitrary function
, Figure 1. Assign an arbitrary function  on
on  and
and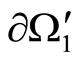 . Use the value of
. Use the value of 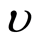 on
on  to plot a harmonic function in
to plot a harmonic function in  and find
and find 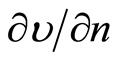 on
on  for this function. Likewise, assign
for this function. Likewise, assign  at
at  and find
and find  at
at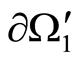 .
.
For the harmonic 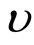 and T we will write down Green’s formula
and T we will write down Green’s formula
 (9)
(9)
Likewise, write Green’s function for 
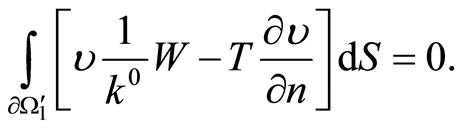 (10)
(10)
Summing up (9) and (10) yields a Green formula for the domain 
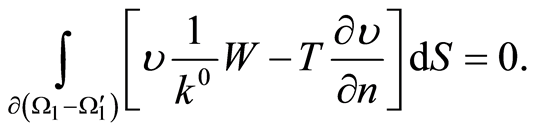 (11)
(11)
On the other hand, once the solution is continuously extendable from  in the domain
in the domain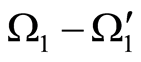 , i.e.
, i.e. , then this solution has its Green’s formula, too
, then this solution has its Green’s formula, too
 (12)
(12)
Diminution of (12) by (11) produces
 (13)
(13)
The integral (13) equals zero for the arbitrary function  whence it follows that
whence it follows that 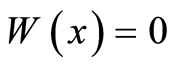 and therefore
and therefore  on
on , then
, then  in the domain. It follow from the harmonicity of
in the domain. It follow from the harmonicity of  in
in 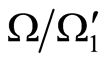 that
that  on
on , i.e.
, i.e. 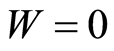 on
on . Thus and so, we arrive at contradiction with the condition of our statement.
. Thus and so, we arrive at contradiction with the condition of our statement.
2) Let ,
, 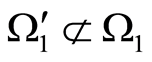 and
and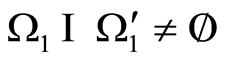 , Figure 2. It can readily be understood that
, Figure 2. It can readily be understood that . Then, inasmuch as
. Then, inasmuch as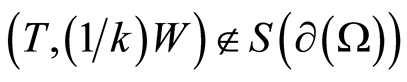 , it is evident that
, it is evident that , i.e., there is an inclusion inside
, i.e., there is an inclusion inside . Let this domain be denoted as
. Let this domain be denoted as . For the inclusion
. For the inclusion  we have
we have  and
and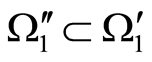 . Then,
. Then,  , on the one hand, and
, on the one hand, and , on the other hand; besides,
, on the other hand; besides, 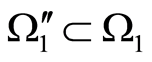 , which agrees with the conditions of paragraph 1 of Statement 5. Thus we come to a contradiction.
, which agrees with the conditions of paragraph 1 of Statement 5. Thus we come to a contradiction.
3) Let , Figure 3. The domain
, Figure 3. The domain  is conditionally divided into two subdomains, one containing
is conditionally divided into two subdomains, one containing , the other containing
, the other containing . The domains are denoted by
. The domains are denoted by  and
and , respectively. Let an inclusion be inside
, respectively. Let an inclusion be inside . Then
. Then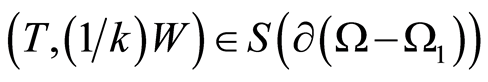 . In this case,
. In this case,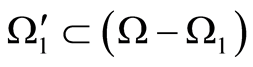 . Whereupon
. Whereupon  is to be fulfilled alongside with
is to be fulfilled alongside with  on
on , which contradicts consequence 1. In case that the inclusion is inside
, which contradicts consequence 1. In case that the inclusion is inside , the relevant considerations will result in the same contradiction.
, the relevant considerations will result in the same contradiction.

figure 1. conditions when one inclusion contains in other.

figure 2. conditions when two inclusions have the general area, i.e. are crossed.

figure 3. conditions when inclusions aren’t crossed.
With the known thermal conductivity coefficient of the host medium, it is possible to find the thermal conductivity coefficient of the inclusion.
Statement 6 (Theory of the unique definition of the thermal conductivity coefficient of inclusion). Let  and
and  be pre-set on
be pre-set on 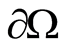 (
( at
at ). Let the medium
). Let the medium  with the thermal conductivity coefficient
with the thermal conductivity coefficient
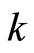 contain an inclusion
contain an inclusion  with the thermal conductivity coefficient
with the thermal conductivity coefficient  and
and  (
( on
on ). Then the condition
). Then the condition 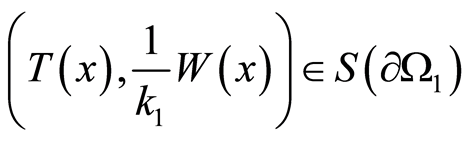 uniquely defines
uniquely defines  for the inclusion.
for the inclusion.
Proof. Assume that  contains two surfaces
contains two surfaces 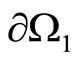 and
and 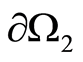 where the settings of the theorem are fulfilled and
where the settings of the theorem are fulfilled and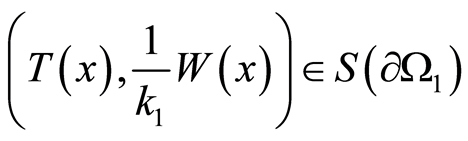 ,
,  ,
, . Likewise Statement 5, a few cases are considered below.
. Likewise Statement 5, a few cases are considered below.
1) Let 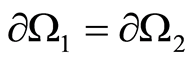 and
and . But if the settings are fulfilled on
. But if the settings are fulfilled on 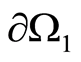 and
and , then, according to consequenceСписок сокращений 1, it must be that
, then, according to consequenceСписок сокращений 1, it must be that . We have arrived at the contradiction.
. We have arrived at the contradiction.
2) Let  Figure 3. The domain
Figure 3. The domain  is conditionally divided into two subdomains, one containing
is conditionally divided into two subdomains, one containing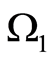 , the other containing
, the other containing . The domains are denoted by
. The domains are denoted by 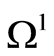 and
and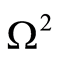 , respectively. Let an inclusion be inside
, respectively. Let an inclusion be inside
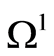 . Accordingly, the domain
. Accordingly, the domain 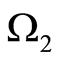 belongs to
belongs to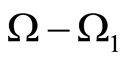 . Under the theorem settings,
. Under the theorem settings,  , then, since
, then, since , we have that
, we have that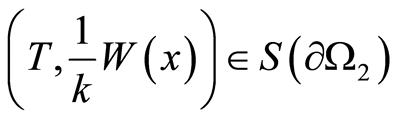 . On the other hand, the condition
. On the other hand, the condition 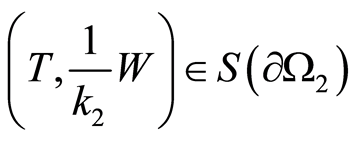 holds true at
holds true at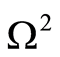 , too. Then, in pursuance to consequence 1, we get
, too. Then, in pursuance to consequence 1, we get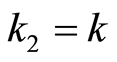 , which is the contradiction. In case that the inclusion is inside
, which is the contradiction. In case that the inclusion is inside , the relevant considerations will reach to the same contradiction.
, the relevant considerations will reach to the same contradiction.
3) Let  or
or  Figure 1. Then
Figure 1. Then  and
and . In other words, we consider the domain
. In other words, we consider the domain 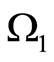 with the inclusion
with the inclusion  and
and . According to the statement 4 we come to a contradiction.
. According to the statement 4 we come to a contradiction.
4) Let ,
,  and
and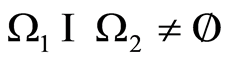 , Figure 2. Continuing the decision with the
, Figure 2. Continuing the decision with the  on
on 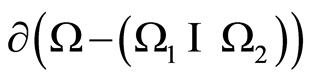 we have
we have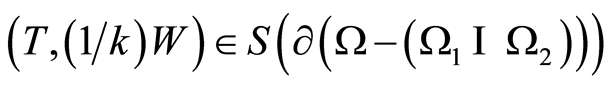 . Then according to the statement 4 inclusion is in
. Then according to the statement 4 inclusion is in . Denoted this domain by
. Denoted this domain by . The domain
. The domain  belongs to
belongs to 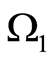 and
and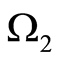 . It follows whereof that
. It follows whereof that 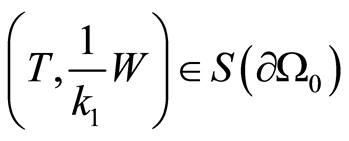 and
and . According to consequence 1, we arrive at
. According to consequence 1, we arrive at , which is the contradiction. The statement has been proved.
, which is the contradiction. The statement has been proved.
The credibility of the criterion 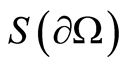 was tested in the two-dimensional calculations. At the side of a unit square
was tested in the two-dimensional calculations. At the side of a unit square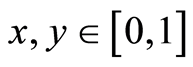 , the values of
, the values of  and
and  in a medium enclosing a circular inclusion were pre-set. The field of the inclusion was modeled by the potentials in the form of
in a medium enclosing a circular inclusion were pre-set. The field of the inclusion was modeled by the potentials in the form of  and
and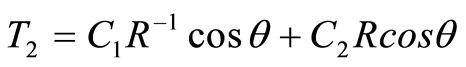 . The field inside the inclusion was described by
. The field inside the inclusion was described by 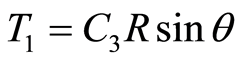 or
or where
where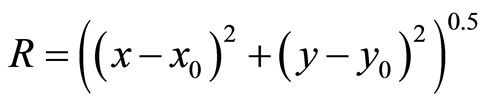 ,
,  are coordinates of the inclusion;
are coordinates of the inclusion; 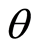 is angle between the vector
is angle between the vector  and axis
and axis . The constant
. The constant  were found from the conjugacy condition (1). The calculations used
were found from the conjugacy condition (1). The calculations used
 ,
, 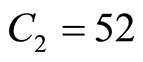 ,
,  ,
,  , where
, where 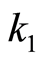 and
and  were the thermal conductivity coefficients of the host medium and inclusion, respectively, and
were the thermal conductivity coefficients of the host medium and inclusion, respectively, and  was the inclusion radius. In a figure 4 calculations for inclusion in the field
was the inclusion radius. In a figure 4 calculations for inclusion in the field 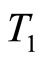 and in a figure 5 in the field
and in a figure 5 in the field  are presented.
are presented.
Figures 4 and 5 show the curves 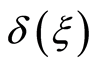 for
for ,
,  , i.e. the point
, i.e. the point  moves over the square side
moves over the square side 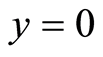 at distance 0.015. Curves 1 and 2 correspond to the values of
at distance 0.015. Curves 1 and 2 correspond to the values of 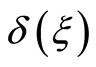 at the distances
at the distances  and
and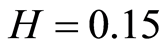 . Values H corresponds to a defect depth under the square side
. Values H corresponds to a defect depth under the square side .
.
As the calculations by the criterion  showed, the inclusion at the occurrence depth
showed, the inclusion at the occurrence depth 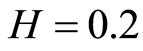 was not revealed; whereas at
was not revealed; whereas at 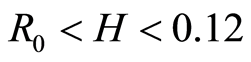 the inclusion was located at high reliability.
the inclusion was located at high reliability.
2. Conclusions
1) The criterion  allows locating inclusions in a body upon the conjugacy condition (1) at the boundary surface.
allows locating inclusions in a body upon the conjugacy condition (1) at the boundary surface.
2) Based on the criterion , both the boundary of the inclusion and its thermal conductivity are uniquely defined.
, both the boundary of the inclusion and its thermal conductivity are uniquely defined.
3) The criterion  is reliable for near-surface inclusions.
is reliable for near-surface inclusions.
The study was supported by the Russian Foundation for Basic Research, Project No. 11-01-00522.
[1] L. S. Sobolev, “Equations of Mathematical Physics,” Nauka, Moscow, 1966.
[2] D. Lesnic, “The Determination of the Thermal Properties of Homogeneous Heat Conductors,” International Journal of Computational Methods, Vol. 1, No. 3, 2004, pp. 431-443. http://dx.doi.org/10.1142/S0219876204000228
[3] M. M. Lavrentiev, “Ill-Posed Problems in Mathematical Physics,” Novosibirsk, 1962.
[4] D. Lesnic, J. R. Berger and P. A. Martin, “A Boundary Element Regularization Method for the Boundary Determination in Potential Corrosion Damage,” Inverse Problems in Engineering, Vol. 10, No. 2, pp. 163-182.
[5] A. A. Schwab, “Computer Tomography Problem Based on the Hologram Interferometry Method,” In: Studies into Conditionally Ill-Posed Problems of Mathematical Physics, Institute of Mathematics SB AS USSR, Novosibirsk, pp. 157-162.
[6] A. A. Schwab, “Boundary Integral Equations for Inverse Problems in Elasticity Theory,” Journal of Elasticity, Vol. 41, No. 3, 1995, pp. 151-160. http://dx.doi.org/10.1007/BF00041872
NOTES
*Corresponding author.