Keywords:CPT; M’PT; Phase Velocity; Travelling Wave Group; Uncertainty Principle; Antiparticle; Pseudo Mass
1. Introduction
This paper was given to the California-Nevada section of the American Physical Society. The subject is a continuation of two preliminary papers [1,2]. These have established the travelling wave group (TWG) as a stable wave packet that contradicts earlier beliefs that the packet is unstable [3]. Operation of the relativistic version of the Klein-Gordon equation on the TWG provides a second order algebraic equation with more than one solution. Dirac assigned his negative eigenvalue for his first order relativistic equation to the positron. However, we find contradictions in his subsequent insistence on its positive mass and positive kinetic energy. However, we preserve the superstructure of quantum electrodynamics by preserving the ratio of charge to mass, e/m, in the antiparticle. This ensures a regular response to electromagnetic fields. It also leads to a new derivation for antiparticle wave functions and to new descriptions for annihilation, creation, mass etc. A sufficiently profound change in method can have surprising consequences.
In particular, it is prima facie anomalous that CPT (Charge, Parity and Time reversal) symmetry violations should be recorded on uncharged particles [4]. CPT symmetry is a consequence of the Principle of Relativity, of the homogeneity of space-time, and of the isotropy of space [5,6]. Time reversal has special significance in antiparticle interactions as expressed in Feynman diagrams and in the Stueckelberg [7]-Feynman [8] “switching principle”: “Negative-energy objects travelling forward in time do not exist; any negative-energy object  travelling backwards in time can and must be described as its anti-object
travelling backwards in time can and must be described as its anti-object  going in the opposite way in space (but endowed with positive energy and motion forward in time)”. This principle, as a function of time, cannot be relegated to the spin part of the wave function; but is naturally incorporated into the TWGs to be described.
going in the opposite way in space (but endowed with positive energy and motion forward in time)”. This principle, as a function of time, cannot be relegated to the spin part of the wave function; but is naturally incorporated into the TWGs to be described.
Quantum mechanics has been chronically debated by the best known names. Einstein [9], Schroedinger and de Broglie employed wavelike models, and the first of these was “led to conclude that the description of reality as given by a wave function is not complete”. Their view contrasts with the more standard methods of Heisenberg and Bohr [10]. Previously, we have shown how Maxwell’s equations, applied to electromagnetic waves, can be quantized by means of a TWG [1]. This wave group satisfies the requirements for Heisenberg’s Uncertainty Principle [3,11] for the case of the massless photon. The group is consistent with Planck’s law, with the de Broglie hypothesis, and with corresponding energy and momentum operators. The wave group is extended to massive particles by adding the conditions derived by special relativity. The same conditions were used by Dirac in his first-order, relativistic equation. His theory has been extraordinarily successful in many ways. Notable examples are the explanation for spin and the prediction of the positron, beside ubiquitous application in high energy elementary particle physics, and in electrodynamics. Nevertheless, the wave packet exists: it can be measured in several ways even while the carrier wave crests appear, move through the wave group, and disappear like “will o’ the wisp”, since the carrier transmits not energy, but phase. It is time for a type of analysis that expounds the consequences of a stable wave packet.
Part of this explanation was already described in the earlier papers, while for clarity, key results are repeated here. Notice that the Dirac equation is a single particle theory and as such does not account for many fundamental processes, such as pair creation and annihilation. However, collisions are made between single particles, and he found that the application of Heisenberg’s dynamics to the free electron gave the unphysical result that its speed is equal to the speed of light c 1. He explained this by noting the velocity with two components: one a lower velocity as measured in the laboratory; and the second a very high frequency oscillation. By use of the TWG, we find that the latter is the phase velocity, the ratio of angular frequency/wave vector, vp = w/|k|; while the former is the group velocity, vg = dw/d|k|. The phase velocity is measurable either through the relation vp = 1/vg 2 in units c = 1, the speed of light in vacuo, or through the ratio w/|k|, corresponding to energy/momentum, where numerators and respective denominators are independently measurable. The identification of properties that break the light barrier provides a simple explanation for what has been called zitterbewegung. This concept has been more useful in developing theories of spin [12,13] than for understanding the spatial part of the wave function. The developments are not used here because we are considering free particles. In free particles, the spin factor in the wave function is independent of the spatial factor and is left to a later time.
2. The Travelling Wave Group
For convenience we use units with the reduced Planck constant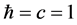 . Write the TWG for the wave function
. Write the TWG for the wave function  of a free particle or photon:
of a free particle or photon:
 (1)
(1)
where A is a normalizing factor found after integration over all space ; and the imaginary argument, in the direction of local propagation k = |k|, represents the Rest Frame Localizer (RFL):
; and the imaginary argument, in the direction of local propagation k = |k|, represents the Rest Frame Localizer (RFL):
 , (2)
, (2)
where X = 0 locates the rest frame3. The equations describe a plane wave travelling with mean wave vector k, mean angular frequency , and therefore with phase velocity vp = ω/|k| and group velocity vg = dω/d|k| 4. The wave vector is the negative gradient of the three dimensional wave function. The second argument in the bracket of equation (1) describes oscillating real and imaginary waves that are enveloped by the Gaussian distribution in the first argument. The envelope is spread by the denominator
, and therefore with phase velocity vp = ω/|k| and group velocity vg = dω/d|k| 4. The wave vector is the negative gradient of the three dimensional wave function. The second argument in the bracket of equation (1) describes oscillating real and imaginary waves that are enveloped by the Gaussian distribution in the first argument. The envelope is spread by the denominator , which is a constant that is set by the initial condition, being an experimental parameter for a free particle. This denominator is related to uncertainty (appendix 6.2) and determines A. The amplitude modulation provided by the envelope causes spreading of k' and ω'—in space and time respectively—about their respective mean values,
, which is a constant that is set by the initial condition, being an experimental parameter for a free particle. This denominator is related to uncertainty (appendix 6.2) and determines A. The amplitude modulation provided by the envelope causes spreading of k' and ω'—in space and time respectively—about their respective mean values,  and k. Notice that the group profile depends only on the envelope, Aexp(−X2/2s2), which in turn varies only with
and k. Notice that the group profile depends only on the envelope, Aexp(−X2/2s2), which in turn varies only with  and t. The Gaussian distribution is constant, covering all
and t. The Gaussian distribution is constant, covering all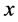 ; all t; and all combinations. The TWG therefore is perfectly stable.
; all t; and all combinations. The TWG therefore is perfectly stable.
In electromagnetism, the real or imaginary parts of the travelling wave represent propagating electric or magnetic fields. With Planck’s law, these fields define in turn the probability for a quantum event, sometimes expressed through perturbation theory. The TWG is adapted to particles as the probability for an event, by operating with the relativistic version of the Klein-Gordon equation. For a free particle the result is the same as in special relativity where:
 . (3)
. (3)
where, by substituting for Planck’s law and for the de Broglie hypothesis, the equation is written:
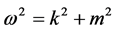 , (4)
, (4)
m now being a quantity similar to rest mass5, by dropping the subscript 0. The fact that the equation is second order has implications for the nature of mass and elementary particles as we shall see. Each of the three variables may be positive or negative, but they are constrained. Consider the differential:
 (5)
(5)
which may be written:
 . (6)
. (6)
So special relativity defines the phase velocity. It is interesting to notice that, if the TWG is considered as the sum of component travelling waves, then a carrier wave component that travels faster than the mean, is slowed by its group velocity according to equation (6). Wave interference ensures that the profile, described by equation (1) as a solution to the wave equation, is preserved in time and space as it follows the mean velocity. General consequences are summarized in Box 1 and described below.
3. Singularities and Symmetries
Begin by representing equation 4 on a right angled triangle [2] and apply Pythagoras’ theorem. Then contract the momentum to the rest state, so that m = w < 0. Now add kinetic energy, as k increases from zero. Suppose, initially, that this kinetic energy is positive, as it is for the electron. The energy would then be represented as in figure 1. Here the electron rest mass is assigned the unit value m0 = 1. Owing to the unphysical singularity that occurs when k = −m, the figure is an illustration of the false supposition.
Notice that figure 1 is one argument among others [2], that are used to solve equation (4) (see summary in box 1). The elimination procedure requires consistency between three conditions: from relativity; from the TWG solution to the wave equation; and from the positive and negative energy solutions found both here in the second order equations, as elsewhere in Dirac’s first order eigenvalues.
Starting from the same rest state, and based on the TWG as a general solution to the wave equation, the analysis [2] shows that a consistent solution is obtained by inverting equation 2 in order to solve for antiparticles: . Thus
. Thus  in a particle transforms to
in a particle transforms to  in the corresponding antiparticle, with reversed angular motion. Wave properties for particles and antiparticles are then represented in figure 2. The figure can be used to illustrate simply, in either two dimensions or three, conservation rules in two particle interactions. For example, in the center of mass frame, energy is conserved on horizontal lines that are symmetric about the abscissa axis (figure 3). Furthermore, the algebraic solution provides an alternative explanation for CPT invariance, but with the clarification that it applies equally to neutral particles as to charged particles. In M’PT invariance, pseudo masses ensure that free particles and corresponding antiparticles have the same symmetries when time reversal is combined with parity.
in the corresponding antiparticle, with reversed angular motion. Wave properties for particles and antiparticles are then represented in figure 2. The figure can be used to illustrate simply, in either two dimensions or three, conservation rules in two particle interactions. For example, in the center of mass frame, energy is conserved on horizontal lines that are symmetric about the abscissa axis (figure 3). Furthermore, the algebraic solution provides an alternative explanation for CPT invariance, but with the clarification that it applies equally to neutral particles as to charged particles. In M’PT invariance, pseudo masses ensure that free particles and corresponding antiparticles have the same symmetries when time reversal is combined with parity.
4. Mass
In the center of mass frame, figure 3 enables a depiction Box 1. The Travelling Wave Group applied to antiparticle wave functions.

of annihilation6 and creation where the properties of energy are contrasted with properties of mass. So Total energy is conserved between the horizontal dashed lines where W = w1 + w2, the sum of two photon energies produced in annihilation. Momentum is conserved because it sums to zero, though for creation from a single gamma ray, a third body is required. At equivalent energies (horizontal dashed lines), particles have less combined momentum, |k3| + |k4|, than photons, |k1| + |k2|. It becomes necessary at this point to comment on the considerations that differentiate the present discussion from earlier and conventional treatments. In the first place, recent experiments, in many disciplines demonstrating entanglement at a distance, require an understanding of the wave packets that were used. Conventional treatments ignore the packet for several reasons: it is assumed unstable; while being subsumed by quantized interactions; and it more often occurs as a real but arbitrary experimental factor. Generally, the quantized interactions depend on the carrier phases; not the packet. However, we have analyzed the consequences for a stable wave group and so are able to consider specific exceptions.
Secondly, we find a description with fewer postulates.
 (a)
(a) (b)
(b)
Figure 1. (a) Calculations for electron group and phase velocities compared with hypothetical group and phase velocities for the positron, by supposing positive kinetic energy superposed on negative pseudo-mass (equation (5)). (b) Corresponding energies for the electron (m = 1); hypothetical positron (m = −1); and massless photon (m = 0). The supposition is unphysical and is not observed experimentally.
For this wave group, the Uncertainty Principle is derived in a simple way that is extensible to unstable packets. We find, in consequence, new information on “pseudo properties”. In relativity, mass tends to infinity as it approaches the speed of light. No “thing” therefore travels faster than the speed of light. However, pseudo properties that do not transport energy, such as the phase velocity, are not so restricted. The information has implications for mass and pseudo mass. This feature differentiates the present work. We do not gloss the problem that occurs when the kinetic energy of a positron is equal to its mass (when k = m in a negatron). It is more difficult to see how this is overcome conventionally, by mixing of states.
However, for reasons of simplicity and clarity, since our wave group is spatial and since our particles are free —i.e. from electromagnetic and nuclear forces—we have not needed to include spinor and bispinor factors in the wave function. Their treatment in relativity is conventional. (By contrast, in atomic physics, spin-orbit coupl-
 (a)
(a) (b)
(b)
Figure 2. (a) Calculated group velocities (<1 = c) and phase velocities (>1) for the electron (k > 0) and its antiparticle (k < 0). (b) Corresponding angular frequencies plotted against wave vector for electrons (upper right) and their antiparticles (lower left). The straight diagonal line plots ω against k in massless photons. Notice, the positron pseudo mass m′ = −m0 when k = 0. The unit of mass is represented as the electron rest mass.
ing makes the spin unseparable in the wave function; but in free particles—i.e. when magnetic vector potential A = 0—the spin becomes, for the spatial part of the wave function, academic.)
5. Conclusion
The Travelling Wave Group enables physical deductions that could not be supported by earlier beliefs in an unstable wave packet. The stability is guaranteed by mean values in the symmetric packet and by conservation of energy and momentum. In particular, analysis of phase

Figure 3. Plot of w versus k for particle antiparticle interactions in the center of mass frame. Energy is conserved W = w1 + w2; while momentum sums to zero K = k1 + k2 = k3 + k4. In annihilation, (|k1| + |k2|) > (|k3| + |k4|).
and group velocities leads to a new way of viewing antiparticle wave functions that are prima facie compatible with the Feynman-Stueckelberg switching principle. Using a suitable modification, the superstructure of quantum electrodynamics is unaffected.
Appendix
Further Consequences
The newly discovered fact of the stable TWG demonstrates a chronic oversight in historic quantum mechanics. Naturally, a feature so fundamental has many consequences, though the wave group is not complete, since some experimental wave packets may be unstable. The TWG is a special window onto a wider world. We have described, in greater detail than previously, the logical consequences of negative mass in 5-dimensional spacetime-mass. This perspective is not new to quantum mechanics [14], but we proceeded to describe the wave function of a free antiparticle. One feature is the infinite phase velocity of the carrier wave in the rest frame, which causes space-time, for it, to be Newtonian. There are many other properties open to investigation. For example, Dirac had difficulty in describing the state of the antiparticle with negative energy. He proposed that such particles are like “holes” in “semiconductor valence bands”. New problems have arisen since his time. What gravitational mass do such bands have, and do they contribute to dark matter? The TWG offers new interpretations for the answers, including a new perspective for the apparent preponderance, in our part of the universe, of matter over antimatter. Again, entanglement at a distance is possible and experimentally observed [15-19] without decay of the photon. Moreover, the wave group allows interactions that are more detailed than series of micro bangs from Schroedinger’s cat; instead, continuous transformations of the wave functions are open to description. There is no end to examples, but our final one provokes the question for an expanding universe, “Which wins, energy or momentum: radiation or mass?” Increasing entropy seems to project decreasing mass with decreasing energy localization. “In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual7”.
Uncertainty in Wave Groups—A Tutorial
Consider two plane waves:
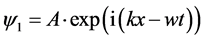 8 and
8 and
 .
.
The real part of the sum of these functions maximizes at t = x = 0.
Show that, generally, the sum is given by:

Identify the wave group envelope.
At time t = 0, Find the first intensity minimum due to destructive interference between the wave groups9.
At distance x = 0, Find the first intensity minimum due to the destructive interference10.
Find the uncertainty at the full width half Maximum11.
Find the condition for the maximum in the wave group envelope for all space and time12, and take the limit as . This gives the group velocity13.
. This gives the group velocity13.
Notice that this wave group is oscillatory. The beats are used to tune pianos. By contrast, Gaussian wave groups do not oscillate.
NOTES
2Similar to Ref 5 section 30, Equation (32).
3One axis being the direction of propagation, k/|k|.
4The derivation is an elementary exercise, (appendix 6.2) provided that suitable conditions are known, such as free particles in vacuo, as presently considered.
5In particles, rest mass is identical to m; in antiparticles, pseudo mass m will have opposite sign.
6The superposition,  , a real function. The electric force e-/m – e-/m′ becomes attractive.
, a real function. The electric force e-/m – e-/m′ becomes attractive.
7Galileo Galilei.
8Symbols are defined in the text.
9x = (/(k.
10t = (/((.
114cos−1(0.5)/(k and 4cos−1(0.5)/((.
12(k·x/2 = ((·t/2.
13d(/dk.