Study of Intermolecular Interactions in Liquid Crystals: Para-butyl-p’-cyano-biphenyl ()
Various characteristics of mesomorphism can be explained using intermolecular interactions between a pair of liquid crystalline molecules. The intermolecular interactions have been calculated considering multipole-multicentere expansion method and modified by second order perturbation treatments. For calculation of multipole i.e. charge, dipole, etc. at each atomic center of molecules, para-butyl-p’-cyano-biphenyl, GAMESS, an ab initio program, with 6-31G
* basis set has been used. The stacking, in-plane and terminal interaction energies explain the liquid crystalline behaviour of the system.
1. Introduction
There are certain substances which do not directly pass from a crystalline solid to an isotropic liquid state and vice versa, rather adopt an intermediate structure which flows like liquids but still possesses the anisotropic physical properties similar to crystalline solids. In view of the wide-spread use of liquid crystals from industrial and technological developments to biomedical applications and display devices, the subject of liquid crystal science has attracted increasing interest of the researchers from different disciplines [1-4]. The peculiar changes— characteristics of mesomorphic behaviour which occur at phase transition, are primarily governed by the nature and strength of intermolecular interactions acting between sides of planes and ends of a pair of molecules [5]. To study the role of molecular interactions in mesogenic compounds, semiempirical calculations have been emphasized with an aim to explain liquid crystallinity [6]. Perrin and Berges have employed PCILO, INDO, CNDO etc. methods to analyse—1) the internal rotations, 2) possibilities of motion in aromatic core as well as in the terminal chains and 3) the influence of the conjugation between oxygen lone pairs and benzene ring on the internal rotations in several mesomorphic compounds [7-9]. Further, it has been argued that detailed analysis of pair interactions between the molecules of crystal lattice is expected to offer a better understanding of mesomorphism [9]. Tokita et al. used Lennard-Jones potential to evaluate intermolecular interactions between a couple of pure nematogens [10]. However, it has been observed that “6-exp” types of potential functions are found to be more effective in explaining the molecular packing instead of Lennard-Jones potentials [11].
In the light of the above facts, intermolecular interaction energy studies in case of some mesogens have been carried out in our laboratory and efforts have been made to explain mesomorphism [12-17]. In continuation of our earlier studies on thermotropic liquid crystals, the present paper embodies the results of both stacking and in-plane intermolecular interactions in case of p-butyl-p’-cyanobiphenyl (4CB) which is a lower homologue of p-alkylp’-cyano-biphenyl series. Thermodynamic parameters reveal that 4CB shows crystal to nematic transition at 48˚C and passes to an isotropic melt state at 16.5˚C [18].
2. Method of Calculation
According to the energy decomposition obtained by perturbation treatment, the total interaction energy ( ) between two molecules is expressed as [19]:
) between two molecules is expressed as [19]:
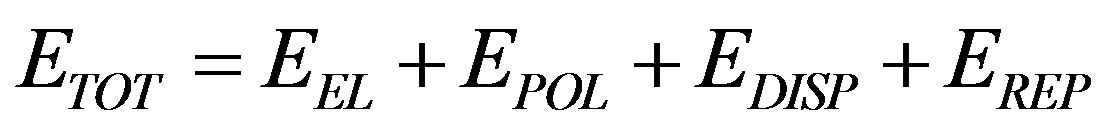
where  and
and  represent electrostatic, polarization, dispersion and repulsion energy components respectively. The formulae for various energy terms are given as under.
represent electrostatic, polarization, dispersion and repulsion energy components respectively. The formulae for various energy terms are given as under.
2.1. Electrostatic Energy
According to the multicentered-multipole expansion method [20], the electrostatic energy term is expressed as:

where ,
, 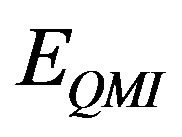 and
and  etc. represent monopolemonopole, monopole-dipole, dipole-dipole and interaction energy terms consisting of multipoles of higher orders respectively. However, consideration upto the first three terms are found to be sufficient for most of the molecular interaction problems [21]. The monopole-monopole energy is given as:
etc. represent monopolemonopole, monopole-dipole, dipole-dipole and interaction energy terms consisting of multipoles of higher orders respectively. However, consideration upto the first three terms are found to be sufficient for most of the molecular interaction problems [21]. The monopole-monopole energy is given as:

where qi and qj are the monopoles at each of the atomic centre of the interacting molecules i and j; 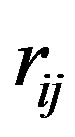 is the inter-atomic distance. The constant, C is a conversion factor, approximately equal to 332 which expresses the energy in kcal/mole of the dimer.
is the inter-atomic distance. The constant, C is a conversion factor, approximately equal to 332 which expresses the energy in kcal/mole of the dimer.
The monopole-dipole energy term is expressed as
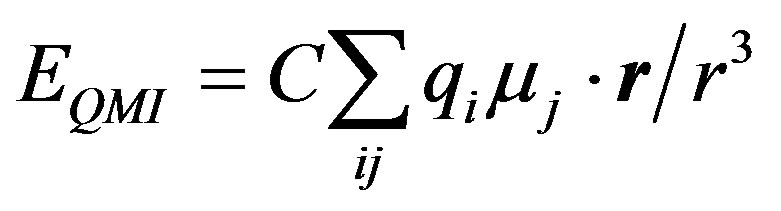
and the dipole-dipole interaction term is given by
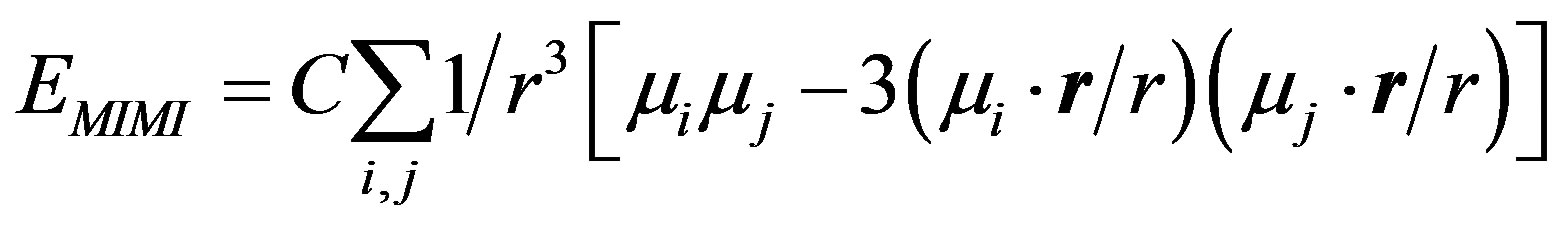
where µi and µj represent atomic dipoles, the subscript of r has been removed without any change in its meaning.
2.2. Polarization Energy
The polarization energy of some molecule (say, s) is obtained as a sum of the polarization energies for the various bonds:
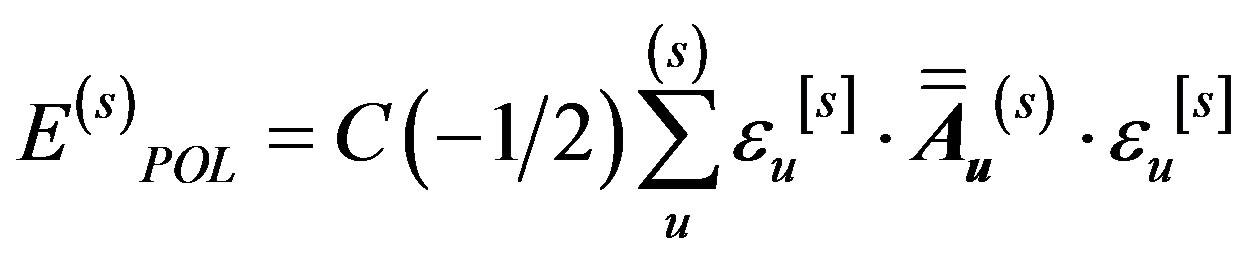 where
where 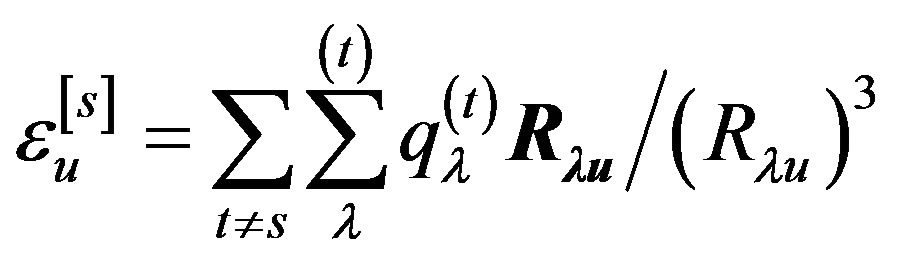 is the electric field created at the bond u by all surrounding molecules and
is the electric field created at the bond u by all surrounding molecules and 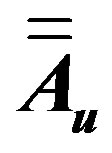 is the polarizability tensor of this bond.
is the polarizability tensor of this bond.  is the vector joining the atom λ in molecule (t) to the centre of polarizable charge on bond u of molecule (s).
is the vector joining the atom λ in molecule (t) to the centre of polarizable charge on bond u of molecule (s).
2.3. Dispersion and Repulsion Energy
Dispersion and repulsion terms are calculated together using Kitaigorodskii type of formula as given below [22-24]:
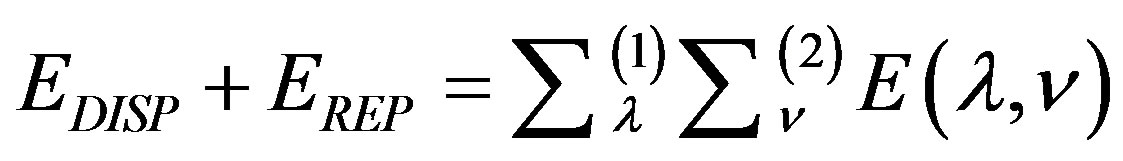
where 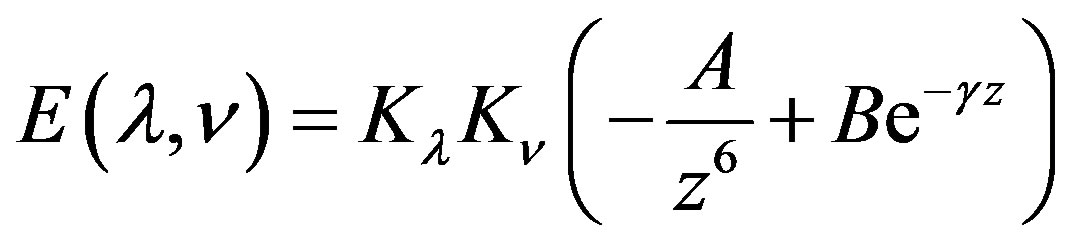
and 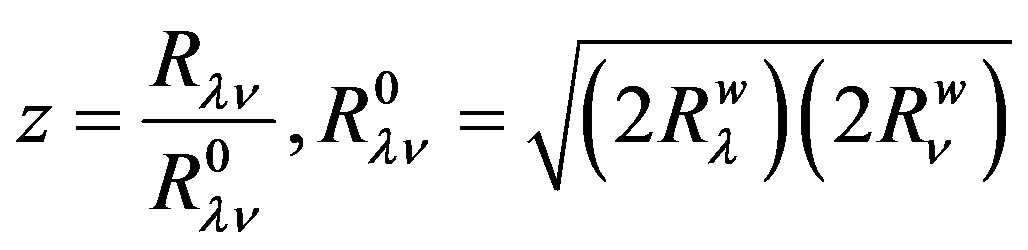
where  and
and  are the van der Waals radii of atoms λ and ν respectively. The parameters A, B and γ do not depend on the atomic species: this necessary dependence is brought about by
are the van der Waals radii of atoms λ and ν respectively. The parameters A, B and γ do not depend on the atomic species: this necessary dependence is brought about by  and the factors
and the factors  and
and  which allow the energy minimum to have different values according to the atomic species involved [24]. The values of these parameters and van der Waals radii have been given by Caillet and Claverie [25,26]. The details of the mathematical formalism may be found in literature [13,19,27,28].
which allow the energy minimum to have different values according to the atomic species involved [24]. The values of these parameters and van der Waals radii have been given by Caillet and Claverie [25,26]. The details of the mathematical formalism may be found in literature [13,19,27,28].
Molecular geometry of 4CB has been constructed using crystallographic data from literature [18]. Net charge and corresponding dipole moment components at each of the atomic centres of the molecule have been computed by GAMESS, an ab initio method, with 6-31G* basis set. The energy minimization has been carried out for both stacking and in-plane interactions separately.
One of the interacting molecules is kept fixed throughout the process while both lateral and angular variations are introduced in the other in all respects relative to the fixed one. The first molecule has been assumed to be in the X-Y plane with X-axis lying along the long molecular axis while origin is chosen approximately at the centre of mass of the molecule. The second molecule has been translated initially along the Z-axis (perpendicular to the molecular plane) and subsequently along Xand Y-axes. Variation of interaction energy with respect to rotation about Z-axis has been examined in the range of ±60˚. Accuracies up to 0.1 Å in sliding (translation) and 1˚ in rotation have been achieved [12,13, 28].
3. Results and Discussion
The schemes of three modes of interactions of a molecular pair are shown in Figure 1. In this figure the consideration of sides, faces and terminals of a molecule has been shown in Figure 1(a). Whereas the three mode of

Figure 1. The three modes of interactions of a molecular pair: (a) Sides, faces and terminals of a molecule; (b) Stacking interaction; (c) In-plane interaction and (d) Terminal interaction.
interaction namely stacking, in-plane and terminal interactions have been shown in Figures 1(b)-(d) respectively. The molecular geometry of 4CB as optimized by GAMESS with 6-31G* basis set is shown in Figure 2 along with various atomic index numbers. Net charge and dipole moment components corresponding to each of the atomic centres have been listed in Table 1. The variation of total interaction energy with respect to inter-planar separation between two stacked 4CB molecules corresponding to four distinct sets of rotations viz. X Y
Y , X
, X Y
Y , X
, X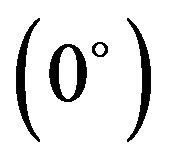 Y
Y and X
and X Y
Y has been shown in Figure 3. It is clear from this figure that optimum inter-planar separation between a pair of 4CB molecules corresponds to 3.0 Å for all the rotational sets. Further, all the interaction energy curves exhibit similar nature. However, the minimum energy stacked configuration is observed for the rotation set, X
has been shown in Figure 3. It is clear from this figure that optimum inter-planar separation between a pair of 4CB molecules corresponds to 3.0 Å for all the rotational sets. Further, all the interaction energy curves exhibit similar nature. However, the minimum energy stacked configuration is observed for the rotation set, X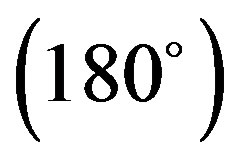 Y
Y where two molecules of 4CB are stacked at an inter-planar separation of 3.0 Å with energy −11.61 kcal/mole. The various components of interaction energy for this case have been depicted in Figure 4. As evident from Figure 4, electrostatic component has no contribution to the stacking interactions as it is always repulsive; polarization component is very weak though it persists over a long range while dispersion energy, which has a major contribution to the total energy plays a decisive role. At shorter distance 3.5 Å, the dispersion energy rapidly decreases and goes to −22.59 kcal/mole which is compensated by simultaneous increase in the short range “exchange” type of forces (repulsion component). The total energy curve exhibits a gross similarity with the Kitaigorodskii curve i.e. the curve showing the sum of dispersion and repulsion energy terms together. Further, dispersion forces are the only major attractions which act between the planes of 4CB molecules and account for a specific stacked geometry. The repulsion component has not been plotted explicitly as it can easily be estimated with the help of dispersion and Kitaigorodskii energy curves.
where two molecules of 4CB are stacked at an inter-planar separation of 3.0 Å with energy −11.61 kcal/mole. The various components of interaction energy for this case have been depicted in Figure 4. As evident from Figure 4, electrostatic component has no contribution to the stacking interactions as it is always repulsive; polarization component is very weak though it persists over a long range while dispersion energy, which has a major contribution to the total energy plays a decisive role. At shorter distance 3.5 Å, the dispersion energy rapidly decreases and goes to −22.59 kcal/mole which is compensated by simultaneous increase in the short range “exchange” type of forces (repulsion component). The total energy curve exhibits a gross similarity with the Kitaigorodskii curve i.e. the curve showing the sum of dispersion and repulsion energy terms together. Further, dispersion forces are the only major attractions which act between the planes of 4CB molecules and account for a specific stacked geometry. The repulsion component has not been plotted explicitly as it can easily be estimated with the help of dispersion and Kitaigorodskii energy curves.
The variation of interaction energy with respect to sliding (translation) of one of the stacked molecules along the long molecular axis (X-axis) corresponding to four fixed rotations about the Z-axis, namely Z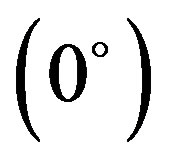 , Z
, Z , Z
, Z and Z
and Z has been shown in Figure 5. Interaction energy has been calculated by giving translations in the range of ±12.0 Å at an interval of 2.0 Å. Here most stable configuration corresponds to Z
has been shown in Figure 5. Interaction energy has been calculated by giving translations in the range of ±12.0 Å at an interval of 2.0 Å. Here most stable configuration corresponds to Z . For this case, various interaction energy components are plotted in Figure 6. It is evident from Figure 6 that monopole-monopole interaction plays a significant role
. For this case, various interaction energy components are plotted in Figure 6. It is evident from Figure 6 that monopole-monopole interaction plays a significant role
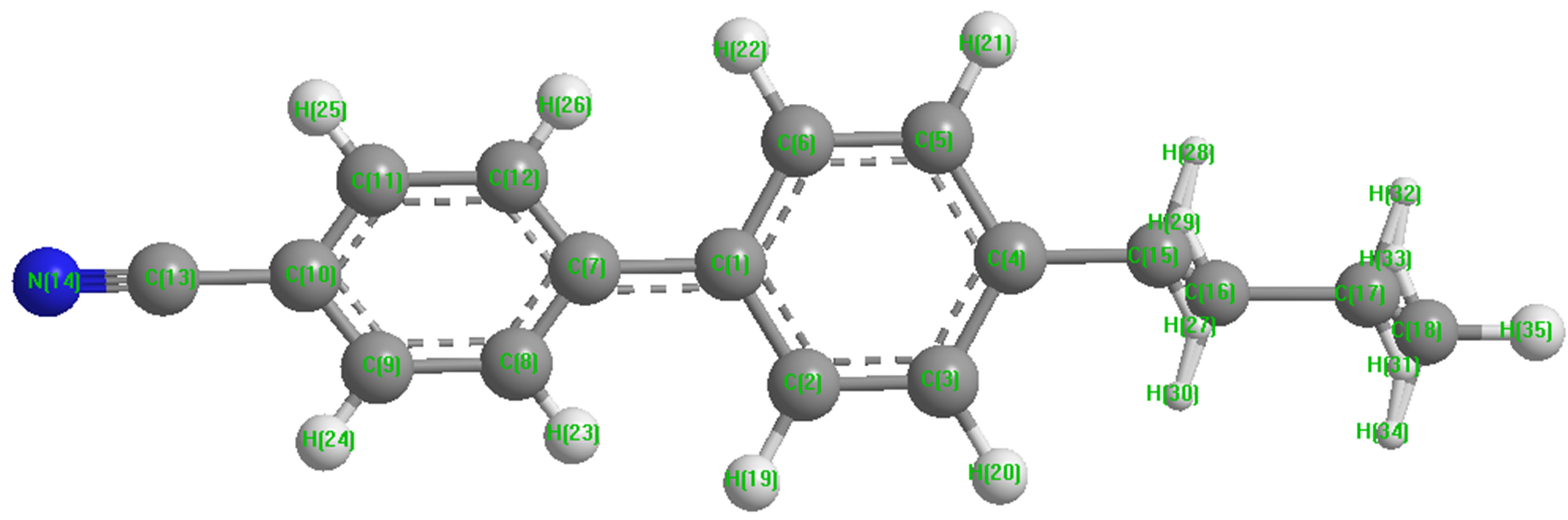
Figure 2. Optimized geometry of 4CB molecule.

Figure 3. Variation of stacking energy with respect to interplanar separation corresponding to four distinct cases of stacking patterns.

Figure 4. Variation of interaction energy components with respect to inter-planar separation for the stacking pattern: X Y
Y .
.

Figure 5. Variation of interaction energy with respect to sliding of one of the stacked molecules along the long molecular axis (X-axis) corresponding to four fixed rotations about the Z-axis.

Figure 6. Variation of interaction energy components with respect to sliding of one of the stacked molecules along the long molecular axis (X-axis) corresponding to Z (0˚).
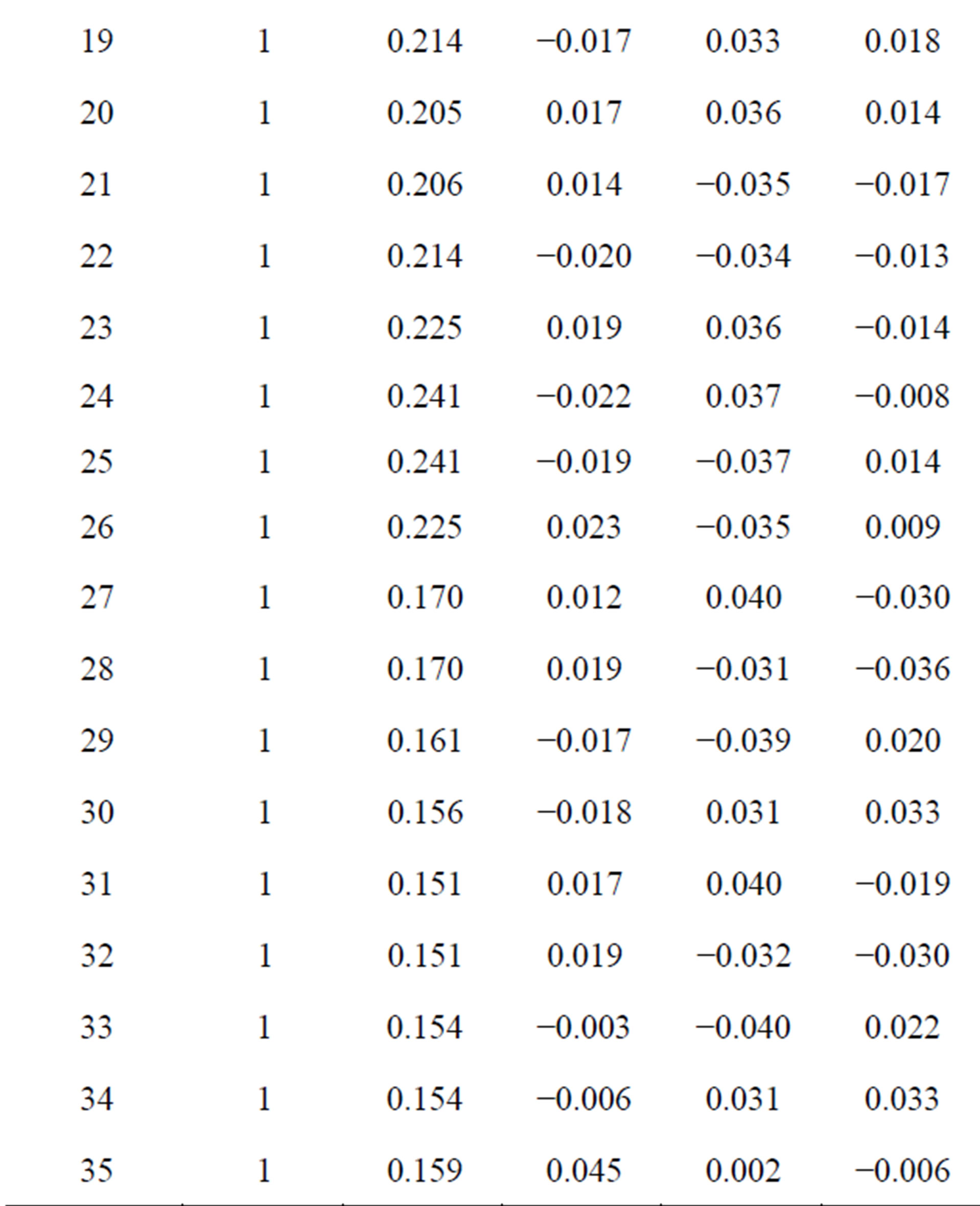
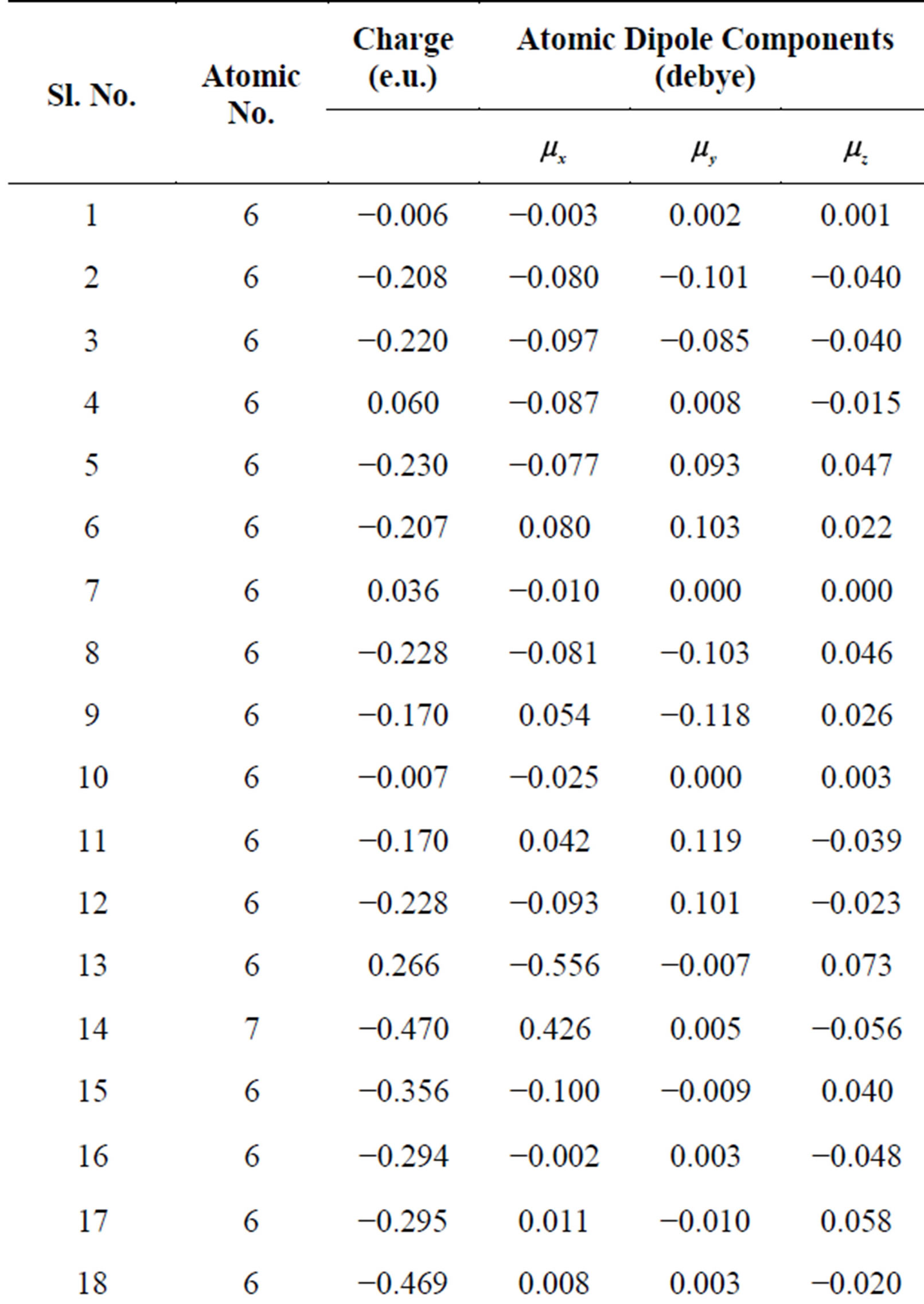
Table 1. Net charge and dipole components corresponding to each atomic centre of the 4CB molecule as computed by an ab initio method, GAMESS with 6-31G* basis set.
within electrostatic terms in comparison to monopoledipole and dipole-dipole interactions. Polarization term is found to be insignificant in stabilizing the molecules in the crystals. Again dispersion components are mainly responsible for the attractions between the pairs of 4CB molecules though the exact optimum point is always located by Kitaigorodskii energy curve which has a gross similarity with the total energy curve. It is interesting to note here that for translation in the range of ±2.0 Å, minor variation in the energy (less than 1.0 kcal/mole) is observed which implies that in the stacked pair of 4CB, molecules can slide one above the other in a range of ±2.0 Å without any significant change in the energy (Figure 5). It must be pointed here that rotations, Z and Z
and Z give energetically less probable stacked geometry. This is because the possibility of stacking at right angles to one another between a pair of molecules capable of mesomorphic phase formation is restricted.
give energetically less probable stacked geometry. This is because the possibility of stacking at right angles to one another between a pair of molecules capable of mesomorphic phase formation is restricted.
The angular dependence of stacking energy components (Figure 7) reveals that both electrostatic and polarization terms have negligible contribution to the total energy. The role of dispersion energy is obviously dominant here although the optimum angle is always governed by Kitaigorodskii term. There is a gross similarity between the curves representing total and Kitaigorodskii energies. Further, for relative orientation of about ±20˚, there occurs a very small change in the stacking energy (less than 1.0 kcal/mole) of the molecular pair.
The energy corresponding to the optimum angle located at 0˚ has been refined with accuracies 1˚ in rotation and 0.1 Å in translation. The final lowest energy stacked geometry, thus obtained, has been shown in Figure 8(a) having an energy −18.52 kcal/mole and inter planar separation 3.0 Å. The in-plane minimum energy configuration which bears energy −5.70 kcal/mole and intermolecular separation 9.1 Å has been shown in Figure 8(b). The details of stacking as well as in-plane energy are listed in Table 2. It seems important to note that the largest attractive contribution in stabilizing the stacked and in-plane interacting pair of 4CB molecules comes from dispersion forces. This supports earlier observations [29,30] and also the basic assumptions of molecular field theory.
The intermolecular interaction energy calculations may reasonably be correlated with the mesomorphic behaviour of the system. When the solid crystals of 4CB molecules are heated, thermal vibrations disturb the molecular ordering of the strongly packed geometrical arrangement of 4CB molecules. Consequently, attractions between the pair of molecules which largely comprise of dispersion forces tend to get weaker at higher temperatures and hence translational freedom along the long molecular axis (Figure 5) and orientational flexibility in a

Table 2. Interaction energy (in kcal/mole) components corresponding to minimum energy configurations of 4CB molecules during stacking, in-plane and terminal interactions.
molecular pair (Figure 7) are considerably enhanced. The freedom of the molecules in a stacked pair to slide along an axis perpendicular to the long molecular axis is energetically restricted. All these parameters favour the nematic behaviour of the system.
The length of molecule is approximately 15 Å, to investigate the terminal interactions away from the van der Waals contacts, the interacting molecule has been shifted along the axis by ±20 Å with respect to fixed one and allowed to rotate along the Xand Y-axis. The energies at such point having examined and found terminal interaction of a pair of 4CB molecule with minimum energy of −2.81 kcal/mole with interplaner separation 4.55 Å.
The minimum energy configuration in case of terminal interaction has been shown in Figure 8(c). Terminal interactions are much weaker than the stacking or in-plane interactions. Rotations about the X-axis show absolutely no preference for any angle, i.e. the molecules are free to rotate about their long molecular axis.
The interaction energy calculation can be correlated with the mesomorphic behavior of the system. When solid crystals of 4CB are heated, thermal vibrations disturb the molecular order of the strongly packed 4CB molecules. Consequently, the attraction within a pair of molecules, largely comprising the dispersion forces, tend to get weaker at higher temperatures, and hence the possibility of relative movement within a molecular pair along the long molecular axis is considerable enhanced. The freedom of molecule in a pair to slide along an axis perpendicular to long molecular axis (Y-axis) is energetically restricted. While terminal interactions, are quite insignificant. The results favour the nematic behaviour of the system. At very high temperature breaking of all dispersion forces results and possible stacking geometry even perpendicular stacking become equally probable which ultimately causes the system to become an isotropic melt.
The most prominent energy minima of above mentioned interactions are refined, and values thus obtained are listed in Table 2 with all contributing terms to enable comparison. These results indicate that the refinement corresponding to the stacking energy at face F1 is maximum and ultimate magnitude of stacking is larger than in-plane and terminal interactions. Further, all possible geometrical arrangements between a molecular pair during stacking, in-plane and terminal interactions have been considered.
4. Conclusion
It may, therefore, be concluded that intermolecular interaction energy calculations are helpful in analyzing the liquid crystallinity in terms of molecular forces. Results favour the nematic behaviour of the system at higher temperatures because the molecules of 4CB are capable of sliding along the long molecular axis with a simultaneous relative orientation of 40˚. At very high temperatures, an all-round breaking of dispersion forces results and all possible stacking geometries (even perpendicular stacking) are almost equally favoured, which ultimately cause the system to pass on to an isotropic melt state.
Acknowledgements
One of us Dr. Manoj Kumar Dwivedi is thankful to UGC, New Delhi for providing financial assistant in the form of JRF/SRF. Authors are also thankful to Dr. Mark S.


Figure 8. (a) Stacked pair of 4CB molecules with minimum energy −18.52 kcal/mole with inter-planer separation of 3.0 Å; (b) In-plane configuration of a pair of 4CB molecules with minimum energy of −5.70 kcal/mole with inter-molecular separation of 9.1 Å and (c) Terminal interaction of a pair of 4CB molecule with minimum energy of −2.81 kcal/mole with inter-planer separation 4.55 Å.
Gordon for providing an ab initio program GAMESS.
NOTES