On the Efficiency for Non-Endoreversible Stirling and Ericsson Cycles ()
1. Introduction
As it is known, thermal engines can be assumed as endothermic or exothermic devices. Among the first, Otto and Diesel engines are the best known; and among the second two devices, Stirling and Ericsson engines are very interesting and similar to the theoretical Carnot engine [1,2]. They are engines closed-cycles regenerative devices initially used for various applications, particularly the Stirling cycle as water pumping and until the middle of last century manufactured on a large scale. But the development of the internal combustion engines from the mid-nineteenth century and the improvement in the refining of fossil fuels influenced the abandonment of the Stirling and the Ericsson engines in the race for industrialization, gradually since the early twentieth century. It is important to point out that Stirling and Ericsson cycles have an efficiency which goes towards the Carnot efficiency as it is shown in some textbooks.
It is also important to point out that a difference between endothermic and exothermic engines is the type of fuel used. While the first mentioned engines need fuel of a certain quality, the other engines can work with lowquality fuels and even alternative sources such as solar energy. Also in exothermic engines the working fluid does not change its composition during the cycle; these engines are quiet and safe but not very powerful. So, since the end of the previous century, and on recent times, Stirling and Ericsson engines characteristics have resulted in renewed interest in the study and design of such engines, and in the analysis of its theoretical idealized cycle, as it is shown in many papers [3-20]. Nevertheless, the discussion on these engines and its theoretical model has not been exhausted.
On other hand, the finite time thermodynamics theory actually is considered an extension of the classical equilibrium thermodynamics in the study of heat engines, in which explicitly is included time dependence of heat transfer processes between reservoirs and engine [21-28]. By excluding the irreversible processes occurring within the working substance, it is obtained the endoreversible cycle, but if the effects of these internal irreversible processes are took into account, the cycle is called non-endoreversible. The exclusion of such effects is known as endoreversibility hypothesis, and is considered for cases in which the internal relaxation time of the working substance is very small compared with the total cycle time. At first Curzon and Ahlborn analyzed the endoreversible Carnot cycle with finite heat transfer between hot and cold thermal reservoirs with temperatures  and
and ,
,  , and the engine. Ideal gas as working substance operating at maximum power output was assumed [21]. The Carnot cycle was modified so that the working substance has
, and the engine. Ideal gas as working substance operating at maximum power output was assumed [21]. The Carnot cycle was modified so that the working substance has  and
and  temperatures different than its reservoirs temperatures, fulfilling TH > THW > TCW > TC. The efficiency for this cycle is known as Curzon-Ahlborn-Novikov-Chambadal efficiency, and it is written by the definition
temperatures different than its reservoirs temperatures, fulfilling TH > THW > TCW > TC. The efficiency for this cycle is known as Curzon-Ahlborn-Novikov-Chambadal efficiency, and it is written by the definition 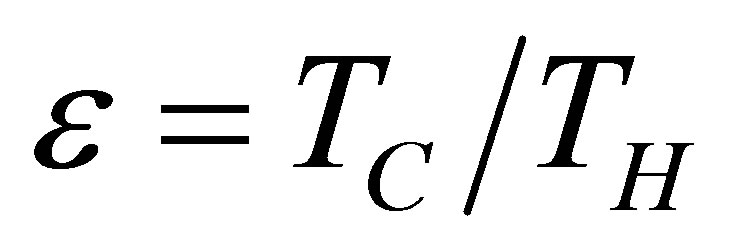 as [29,30],
as [29,30],
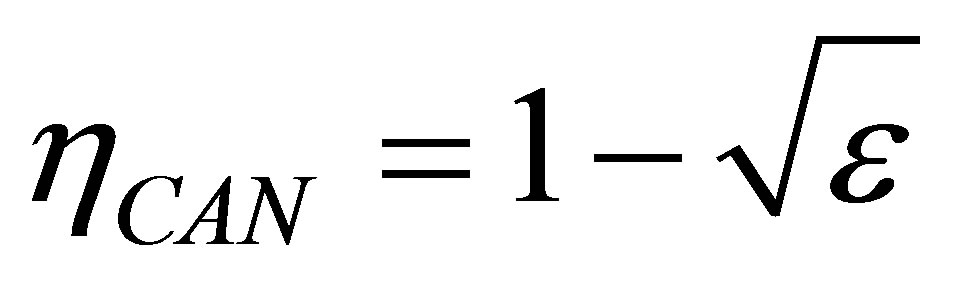 (1)
(1)
In addition, as it is known, Carnot cycle in the classical equilibrium thermodynamics context is a cycle in which the working substance during the isothermal processes has the same temperature as the reservoirs,  and
and , with the efficiency,
, with the efficiency,
 . (2)
. (2)
References [8,11-20] are devoted to analysis of Stirling and Ericsson cycles in the finite time thermodynamics point of view. Particularly, with a similar analysis made by Curzon and Ahlborn [21], Angulo-Brown and Ramos-Madrigal analyzed these cycles [8], finding that its efficiency is towards efficiency given in (1).
On the other hand, it is known that real heat engines have internal processes that influence its performance. This is reason enough to consider an analysis of non endoreversible cycles. Several authors have addressed these problems as Ibrahim et al. [31], Chen [32], and Velasco et al. [33], among others, which analyzed the non-endoreversible Curzon and Ahlborn cycle.
Ibrahim et al. [31] showed the efficiency at maximum power of some cycles equal (or approximated to) , where
, where  is a parameter to take into account internal irreversibilities in the cycle, with 0 <
is a parameter to take into account internal irreversibilities in the cycle, with 0 <  ≤ 1. In the cycle without internal irreversibilities
≤ 1. In the cycle without internal irreversibilities . Chen [32] included this parameter as
. Chen [32] included this parameter as 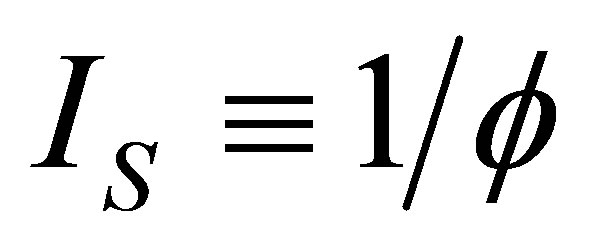 and wrote the efficiency of a Curzon and Ahlborn cycle heat engine at maximum power given as
and wrote the efficiency of a Curzon and Ahlborn cycle heat engine at maximum power given as , with
, with . Velasco et al. [33] assumed the parameter
. Velasco et al. [33] assumed the parameter  as a
as a  -independent parameter, and showed that
-independent parameter, and showed that 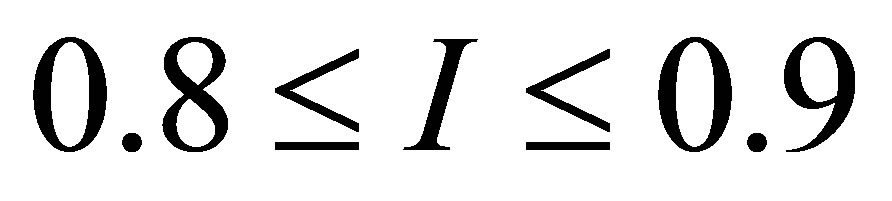 for typical power plants with water as working fluid. Moreover, an adequate model of performance for modern plants is the ecological function, approached by Angulo-Brown [34], and in the maximum ecological function regime was found the efficiency
for typical power plants with water as working fluid. Moreover, an adequate model of performance for modern plants is the ecological function, approached by Angulo-Brown [34], and in the maximum ecological function regime was found the efficiency
 for the non-endoreversible Curzon and Ahlborn cycle [35].
for the non-endoreversible Curzon and Ahlborn cycle [35].
Therefore, in the present paper, an analysis of the Stirling and Ericsson cycles from the viewpoint of finite time thermodynamics is now made. Assuming the existence of internal irreversibilities in an engine modeled by any of these cycles, it is shown modified expressions for the power output and ecological function, and examines how one can build the expression for the efficiency in both regimes, maximum power output and maximum ecological function. Some results from [8] are used, in order to obtain expressions for power output, ecological function and efficiency, similar to those obtained in [31,32, 35]. Variable changes are made, like those used in Gutkowicz-Krusin et al. [24], and Ladino-Luna [36]. This paper has two purposes; the first one is to show a methodology for writing objective functions including compression ratio as an important parameter; the second one is to show how in the context of finite time thermodynamics the Stirling and Ericsson cycles have an efficiency that in their limit cases is always reduced to the Curzon and Ahlborn cycle efficiency, as in classical equilibrium thermodynamics these cycles have an efficiency like the Carnot cycle efficiency.
2. Stirling Cycle
To construct expressions for power output and ecological function it is necessary make some initial assumptions. First, heat transfer of the process of the cycle is supposed to occur as Newton’s cooling law for two bodies in thermal contact with temperatures 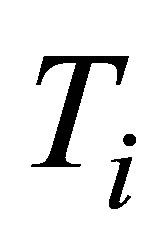 and
and ,
,  , with a rapidity of heat change
, with a rapidity of heat change , and a constant thermal conductance
, and a constant thermal conductance , which for convenience is assumed to be equal in all cases of heat transfer,
, which for convenience is assumed to be equal in all cases of heat transfer,
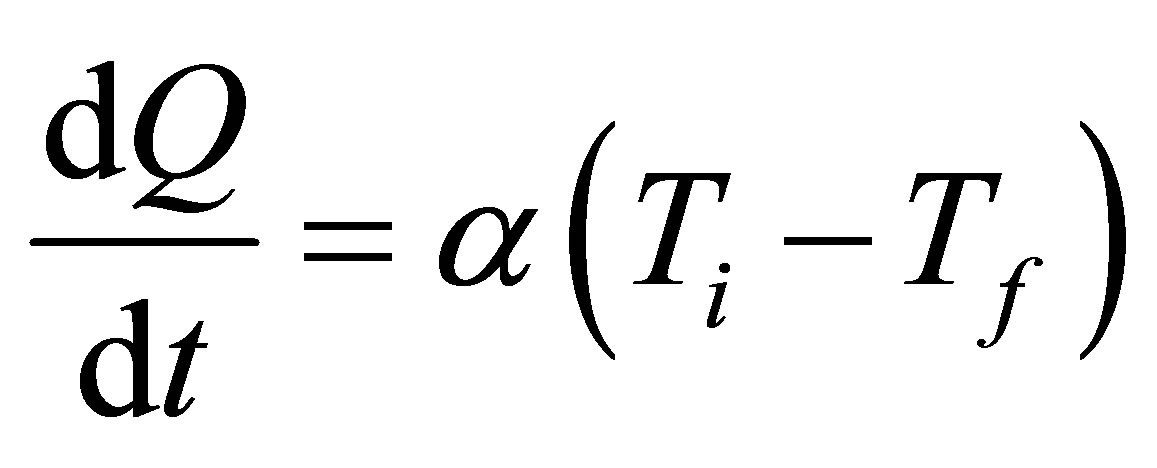 . (3)
. (3)
On the other hand, it is assumed that the internal processes of the system cause irreversibilities that can be represented by a factor 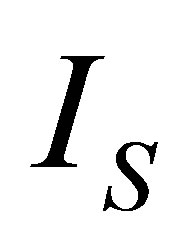 [36], so from the second law of thermodynamics can be written
[36], so from the second law of thermodynamics can be written
 . (4)
. (4)
Power output is defined as,
 , (5)
, (5)
where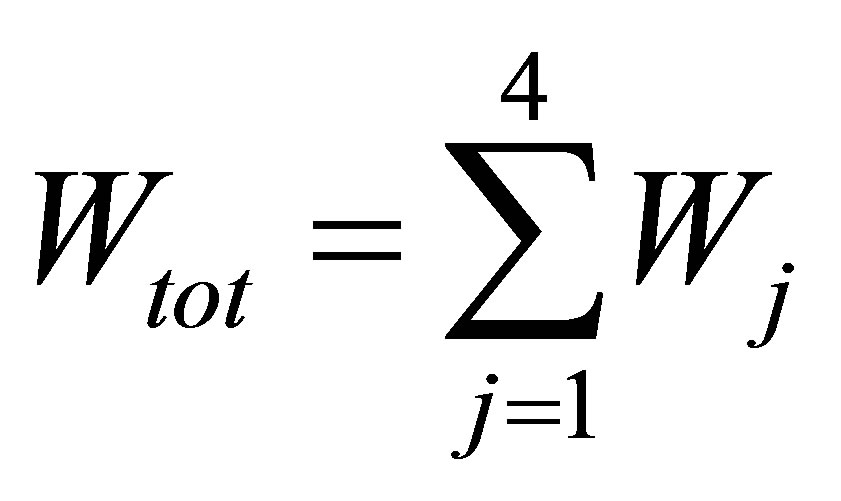 ,
,  work by the system in the j-th process,
work by the system in the j-th process,  ,
,  time of j-th process.
time of j-th process.
Similarly the entropy production and the ecological function can be constructed taking into account (3) and (4), from its definition, i.e.,
 , (6)
, (6)
and the ecological function also,
 . (7)
. (7)
As [24] shows, for an ideal gas as working substance in case of an isothermal process the equation of state leads to,
 . (8)
. (8)
Now, as it is known, Stirling cycle consists of two isochoric processes and two isothermal processes. At finite time is considered the difference between the temperatures of reservoirs and the corresponding operating temperatures, similarly to those of Curzon and Ahlborn cycle [21], as shown in Figure 1.
A fundamental assumption for this cycle is that the heating and cooling at constant volume are performed as, Escuchar
 , (9)
, (9)
where it is not dificult to show that it meets,
 . (10)
. (10)
On other hand, from the equilibrium conditions it can be assumed,
 , (11)
, (11)
and since the heat of heating and cooling respectively, from the first law of thermodynamics,
 (12a)
(12a)
and
 , (12b)
, (12b)
and the time for each of isochoric processes are given as,
 . (13)
. (13)
The time for the isothermal processes can be found from (8) as,
 (14a)
(14a)
and

Figure 1. Idealized Stirling cycle at the V − p (volume vs pressure) plane.
 , (14b)
, (14b)
where the negative sign in (14b) is presented because there is no negative time, and the total time of the cycle is now,
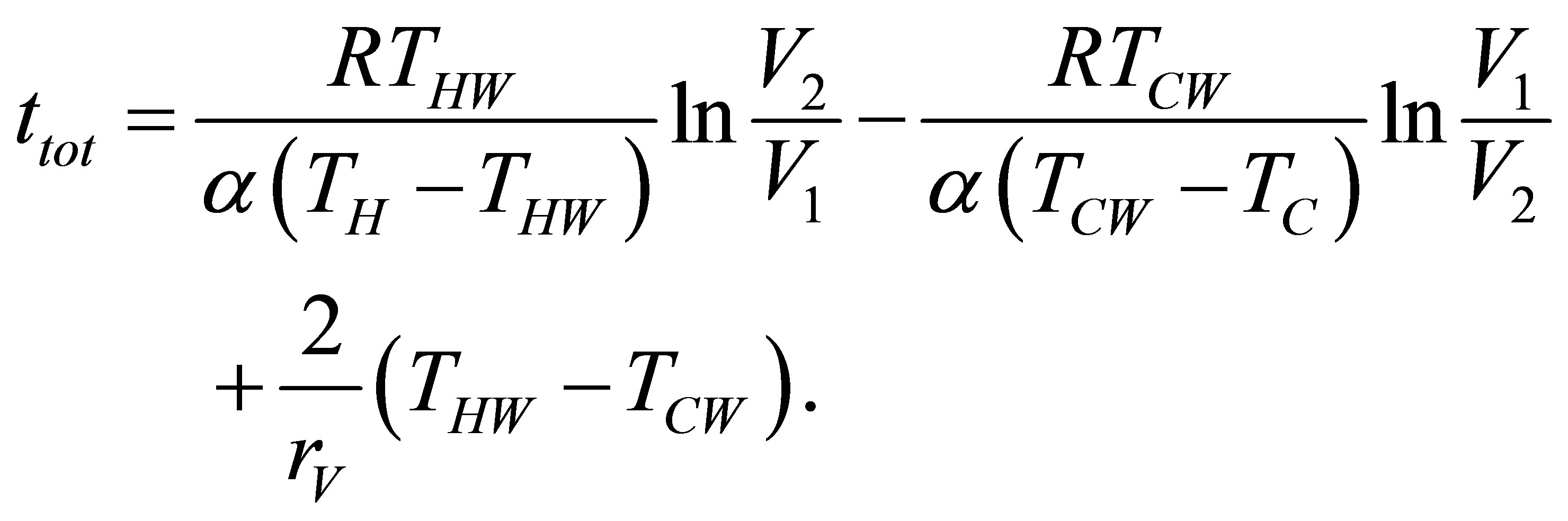 (15)
(15)
So, since its definition and taking into account (4) power output of cycle is writen as,
 . (16)
. (16)
Now with the change of variables used in Ladino-Luna [35],
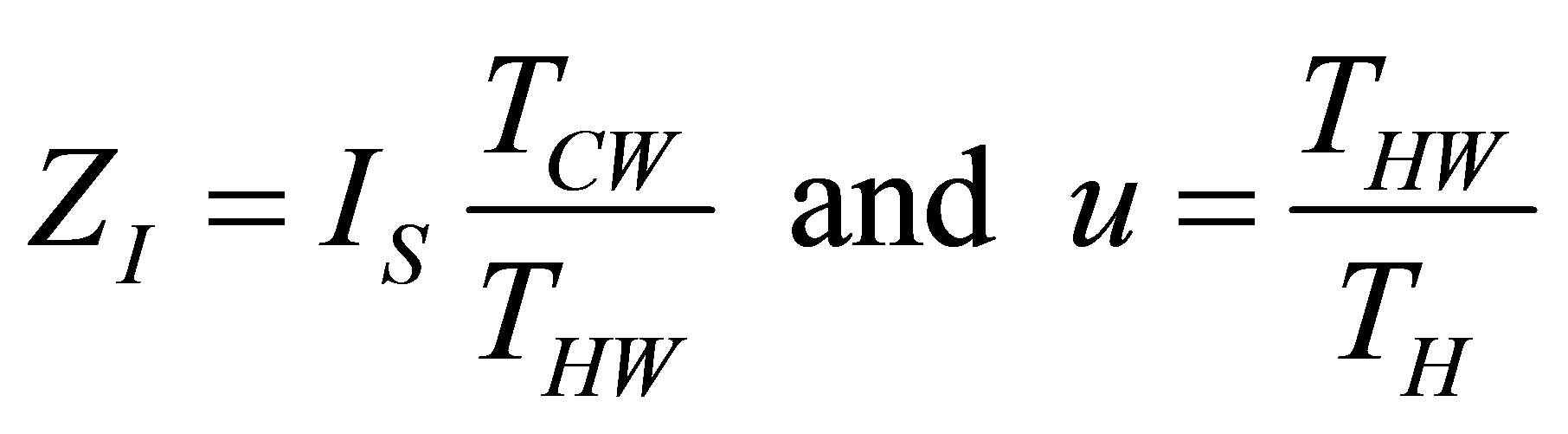 (17)
(17)
and taking into account the ratio of temperatures of the heat reservoirs, used in (1) and (2), with the parameter
 that includes the compression ratio of cycle
that includes the compression ratio of cycle , the power output of Stirling cycle takes the form,
, the power output of Stirling cycle takes the form,
 . (18)
. (18)
The optimization conditions 
and  permit find the function
permit find the function 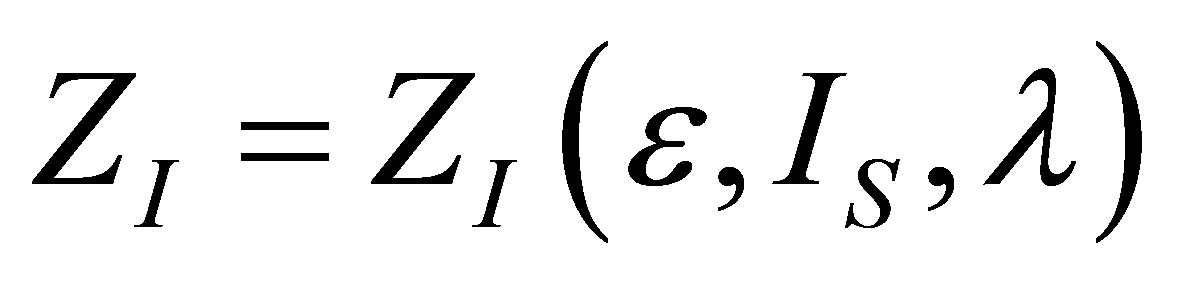 . From the first one it is obtain
. From the first one it is obtain  as,
as,
 . (19)
. (19)
and from the second one a solution physically adequate  can be obtained by
can be obtained by
 (20)
(20)
so that the efficiency at maximum power output can be written as,
 , (21)
, (21)
for known values of parameters  and
and . In the limit
. In the limit , namely
, namely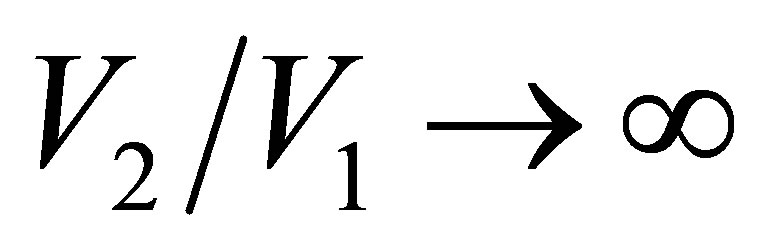 , the efficiency of non-endoreversible Stirling cycle,
, the efficiency of non-endoreversible Stirling cycle, 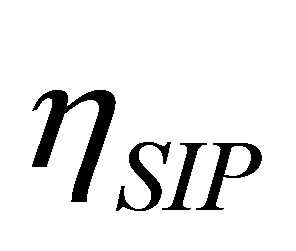 , goes to the efficiency for the non-endoreversible Curzon and Ahlborn cycle [33], as can be seen from (20),
, goes to the efficiency for the non-endoreversible Curzon and Ahlborn cycle [33], as can be seen from (20),
 . (22)
. (22)
The analysis for the case of ecological function is similar to the case of power output, and also leads to similar results. The shape of the function 
is the same as in (19), but the form of 
changes due to ecological function can be interpreted as an effective power output obtained of the heat engine. The simplest expression of ecological function is as (7) [34], where  is the temperature of the cold reservoir and
is the temperature of the cold reservoir and  is the entropy production definite as (6). Because heating and cooling in both isochoric and isobaric processes are considered constant, and taking into account (4) and (10), the change of entropy can be taken only for isothermal processes. Consequently the change of entropy for the non-endoreversible cycle considered is,
is the entropy production definite as (6). Because heating and cooling in both isochoric and isobaric processes are considered constant, and taking into account (4) and (10), the change of entropy can be taken only for isothermal processes. Consequently the change of entropy for the non-endoreversible cycle considered is,
 , (23)
, (23)
which leads to the ecological function as,
 (24)
(24)
where  is as (15). With the same parameters definite in (17) ecological function can be written now as,
is as (15). With the same parameters definite in (17) ecological function can be written now as,
 . (25)
. (25)
As in the case of power output optimizing, in order to find the efficiency at maximum ecological function there are also two conditions, namely 
and . These conditions lead to obtaining the parameter
. These conditions lead to obtaining the parameter  as in (19) and also
as in (19) and also  as an adequate solution for the second condition by the relation,
as an adequate solution for the second condition by the relation,
 (26)
(26)
The efficiency for the Stirling cycle at maximum ecological function can be written now as,
 , (27)
, (27)
and also in the limit  goes towards the efficiency for non-endoreversible Curzon and Ahlborn cycle by (26), i.e.,
goes towards the efficiency for non-endoreversible Curzon and Ahlborn cycle by (26), i.e.,
 . (28)
. (28)
The existence of a finite heat transfer in the isothermal processes and the assumption of constant heating and cooling are affected with the assumption of a nonendoreversible cycle with ideal gas as working substance. However, the general form of power and ecological function of such analyzed cycles is similar to the corresponding previous expresions, obtained in the literature of finite time thermodynamics. One can see that  implies instantaneous adiabats in the case of Curzon and Ahlborn cycle, and the expresions for power output, ecological function and the corresponding eficiencies are the same as in Ladino-Luna [35,36].
implies instantaneous adiabats in the case of Curzon and Ahlborn cycle, and the expresions for power output, ecological function and the corresponding eficiencies are the same as in Ladino-Luna [35,36].
Power output and ecological function have also an issue that shows direct dependence on the temperature of the working substance. Figures 2 and 3 show the approach of efficiencies obtained from (20) and (26) to the previously efficiencies found [31,32,35], for different values of compression ratio and assuming constant values to the parameters involved. In these figures can be appreciate that including besides the limit 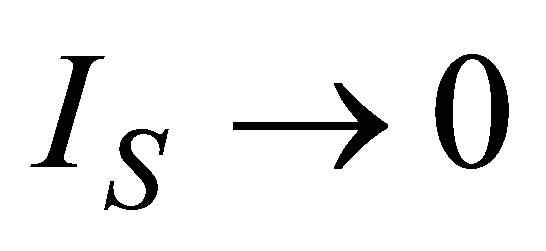 leads to the obtained expresions in Angulo-Brown and Ramos-Madrigal [8], but with the parameters used in the present paper.
leads to the obtained expresions in Angulo-Brown and Ramos-Madrigal [8], but with the parameters used in the present paper.
Expressions obtained with the changes of variable suggested in (17) have the virtue of leading directly to the shape of the efficiency through the function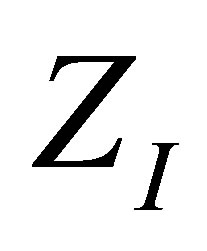 . Figures 2 and 3 show as in classical equilibrium ther-
. Figures 2 and 3 show as in classical equilibrium ther-
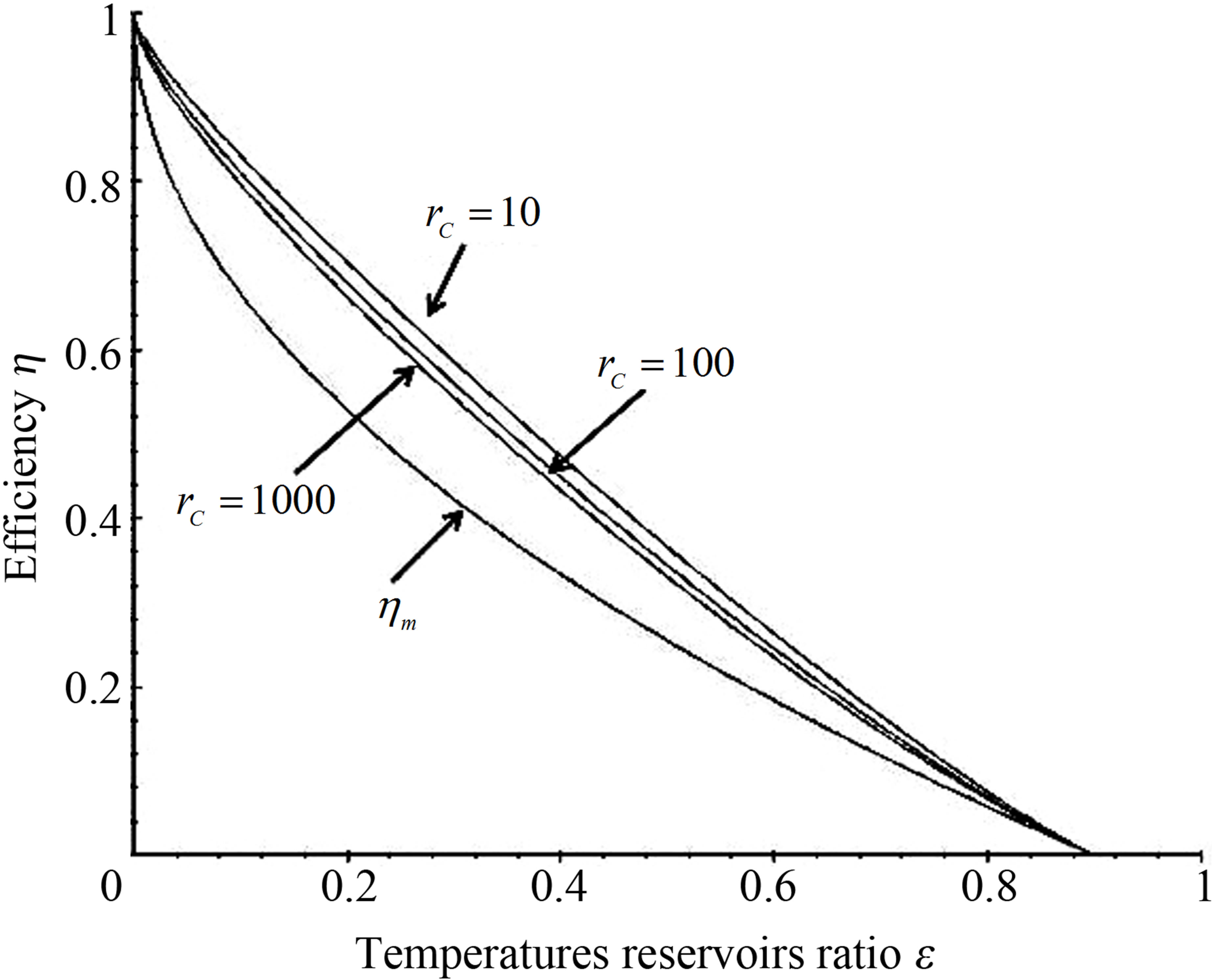
Figure 2. Comparison of resulting efficiencies from (20) with eficiencies in references [31,32].

Figure 3. Comparison of resulting efficiencies from (26) with the efficiency in reference [35].
modynamics that the Stirling cycle has efficiency like the Carnot cycle efficiency, and how in the context of finite time thermodynamic this cycle has efficiency that in their limit cases is always reduced to the Curzon and Ahlborn cycle efficiency.
3. Ericsson Cycle
The Ericsson cycle, consisting of two isobaric processes and two isothermal processes is shown in Figure 4. Now, it is follows a similar procedure as in the Stirling cycle case.
The hypothesis on constant heating and cooling but now at constant pressure is expressed as,
 . (29)
. (29)
So is true that,
 (30)
(30)
The equilibrium condition now is,
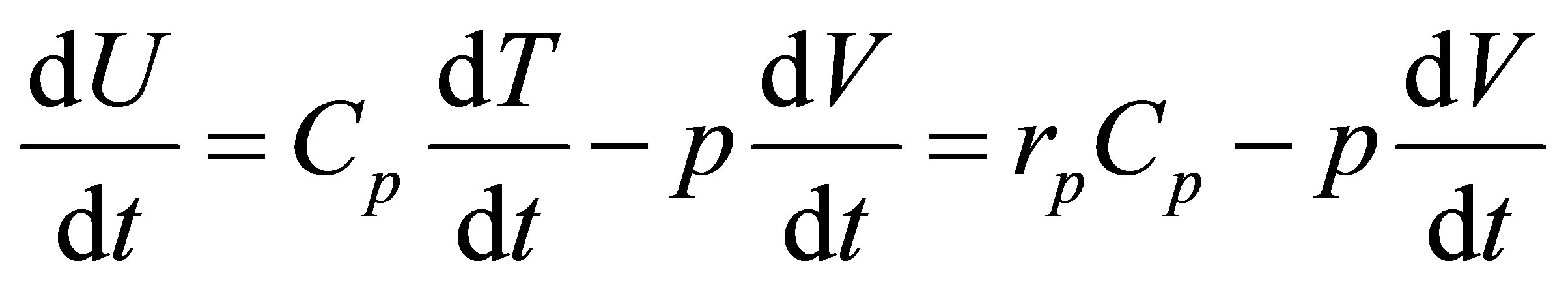 , (31)
, (31)
so the time for a constant pressure process is given as,
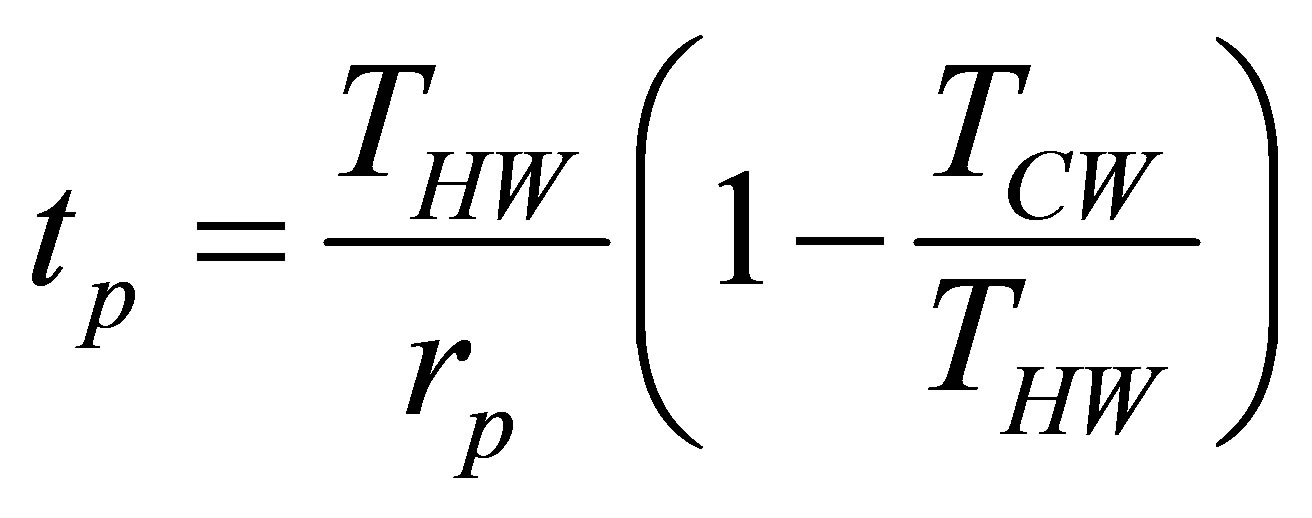 . (32)
. (32)
and the time for the isothermal processes also can be obtained from (8), and can be written as,
 (33)
(33)
and the total time of cycle is now,
 (34)
(34)

Figure 4. Idealized Ericsson cycle at the the V − p (volume vs pressure) plane.
and the power output of cycle from its definition and taking into account (4) remains,
 . (35)
. (35)
With the change of variables suggested in (17) now the expression for the power output of non-endoreversible Ericsson cycle is,
 (36)
(36)
which is essentially equal to that found for the Stirling cycle, with the only variation in the factor  instead of
instead of . For extreme conditions
. For extreme conditions  and
and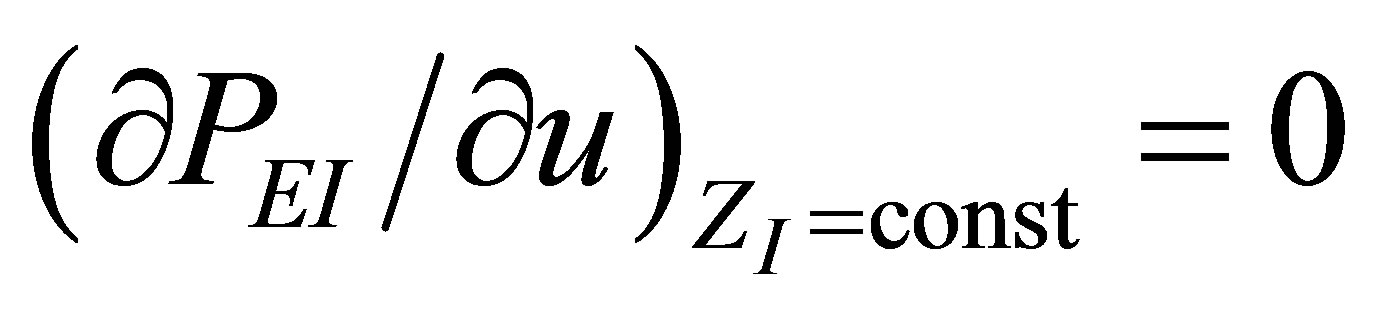 , it is obtained again the expression (19), allowing us to find a physically acceptable solution
, it is obtained again the expression (19), allowing us to find a physically acceptable solution 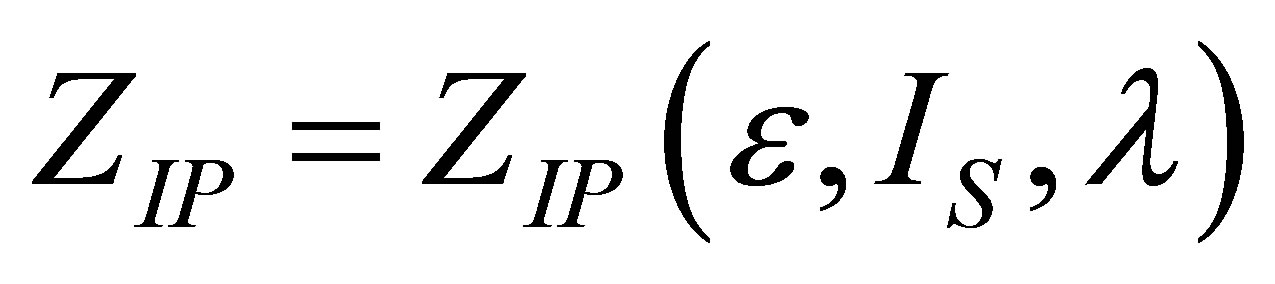 by,
by,
 (37)
(37)
So, at maximum power output condition the efficiency of non-endoreversible Ericsson cycle can be written as,
 . (38)
. (38)
The analysis for the case of ecological function is similar to the case of power output, and also leads to similar results. The shape of the function 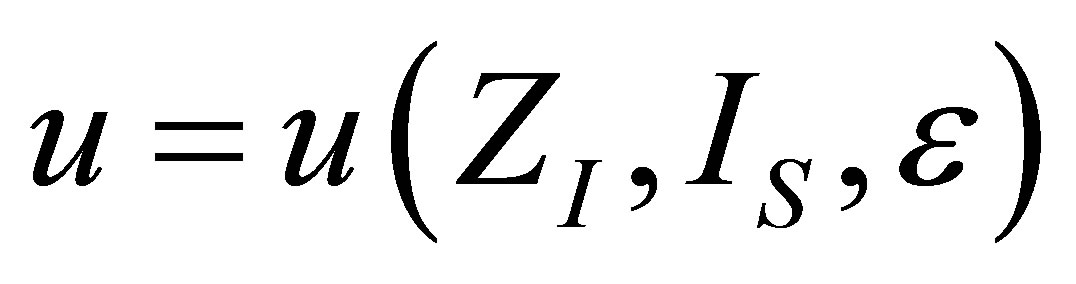 is the same as in (19), but the form of
is the same as in (19), but the form of  changes due to ecological function can be interpreted as an effective power output obtained of the heat engine.
changes due to ecological function can be interpreted as an effective power output obtained of the heat engine.
Again using the simplest expression of ecological function and because heating and cooling in isobaric processes are considering constant, the change of entropy can be taken only for the isothermal processes. Consequently the change of entropy for the non-endoreversible Ericsson cycle considered is as,
 , (39)
, (39)
from which the ecological function is,
 , (40)
, (40)
and substituting in (40) the total time (34), ecological function for the Ericsson cycle can be written as,
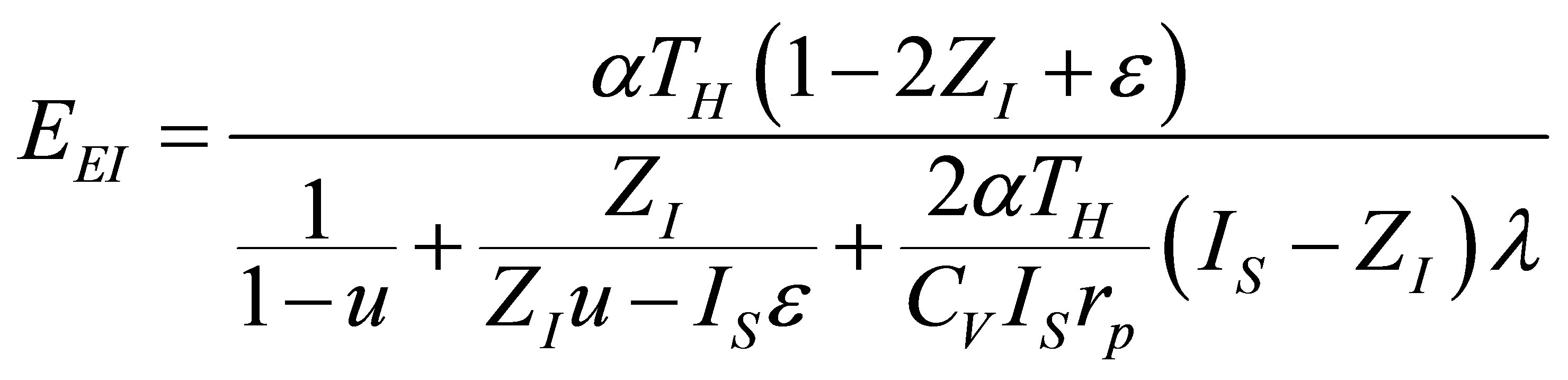 , (41)
, (41)
where the parameter  takes the adequate value depending on the cycle analyzed.
takes the adequate value depending on the cycle analyzed.
As in the case of power output optimizing, there are two conditions for the ecological efficiency at maximum ecological function, i.e,  and
and . These conditions lead to obtain parameter
. These conditions lead to obtain parameter  as in (19), and also
as in (19), and also  by
by
 (42)
(42)
The efficiency for Ericsson cycle at maximum ecological function can be written now as
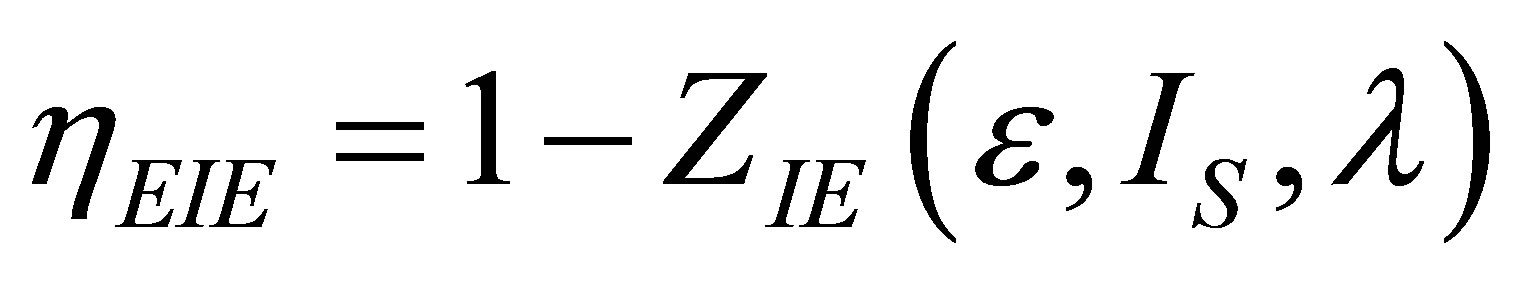 . (43)
. (43)
4. Concluding Remarks
The developed methodology leads directly to appropriate expressions of the objective functions simplifying the optimization process, and this methodology shows the consequences of assuming non-endoreversible cyle in the process of isothermal heat transfer through the factor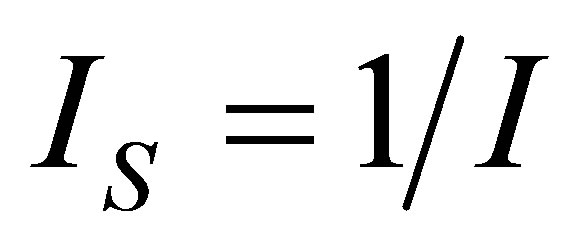 , which represents the internal irreversibilities of cycle [31], so that the proposed heat engine model is closer to a real engine. On other hand, as the known Carnot theorem provided a level of operation of heat engines, the Curzon and Ahlborn cycle provides levels of operation of such engines closer to reality. In this sense, the same manner within the context of classical equilibrium thermodynamics shows that in any cycle formed by two isothermal processes and any other pair of the same processes (isobaric, isochoric, adiabatic), efficiency tends to Carnot cycle efficiency, in the context of finite time thermodynamics, any cycle as previously mentioned has an efficiency which tends to Curzon and Ahlborn cycle efficiency. The above statements are independent if the cycle is considered endoreversible or non-endoreversible.
, which represents the internal irreversibilities of cycle [31], so that the proposed heat engine model is closer to a real engine. On other hand, as the known Carnot theorem provided a level of operation of heat engines, the Curzon and Ahlborn cycle provides levels of operation of such engines closer to reality. In this sense, the same manner within the context of classical equilibrium thermodynamics shows that in any cycle formed by two isothermal processes and any other pair of the same processes (isobaric, isochoric, adiabatic), efficiency tends to Carnot cycle efficiency, in the context of finite time thermodynamics, any cycle as previously mentioned has an efficiency which tends to Curzon and Ahlborn cycle efficiency. The above statements are independent if the cycle is considered endoreversible or non-endoreversible.
5. Acknowledgements
The authors thank the partial support of CONACYT (México) by the SNI program.