Predicting Rainfall Using the Principles of Fuzzy Set Theory and Reliability Analysis ()
1. Introduction
First fuzzy set concepts are discussed followed by principles of reliability analysis. This work is an extension of the work done by Hasan et al. [1]. In predicting weather conditions, factors in the antecedent and consequent parts that exhibit vagueness and ambiguity are being treated with logic and valid algorithms by Hasan et al. [2]. Use of fuzzy set theory has been proved by scientists to be applicable with uncertain, vague and qualitative expressions of the system. Application of fuzzy set theory in soil, crop, and water management is still in its infant stage due to the lack of awareness of the potentials of fuzzy set theory. Weather forecasting is one of the most important and demanding operational responsibilities carried out by meteorological services worldwide. It is a complicated procedure that includes numerous specialized technological fields. The task is complicated in the field of meteorology because all decisions are made within a visage of uncertainty associated with weather systems. Chaotic features associated with atmospheric phenomena have also attracted the attention of modern scientists. The drawback of statistical models is a foundation, in most cases, upon several tacit assumptions regarding the system mentioned by Wilks [3]. Carrano et al., [4] compared non-linear regression modeling and fuzzy knowledge-based modeling, and explained that fuzzy models were most appropriate when subjective and qualitative data were utilized and the numbers of empirical observations were small. Brown-Brandl et al. [5] used four modeling techniques to predict respiration rate as an indicator of stress in livestock. Four modeling techniques consisted of two multiple regression and two fuzzy inference systems. Fuzzy inference models offered better results than the two multiple regression models (Brown-Brandl et al. [5]). Fuzzy inference models yielded a lower percentage of error when compared to the linear multiple regression model (Hasan et al., [2]). Similar research by Wong et al. [6] compared the results of fuzzy rule based rainfall prediction with an established method which used radial basis function networks and orographic effect. They concluded that fuzzy rule based methods could provide similar results from the established method. However, the method has an advantage of allowing the analyst to understand and interact with the model using fuzzy rules. Lee et al. [7] considered two smaller areas where they assumed precipitation was proportional to elevation. Predictions of those two areas were made using a simple linear regression based on elevation information only. Comparison with the observed data revealed that the radial basis function (RBF) network produced better results than the linear regression models. Hence, considering the advantage of using the concept of fuzzy logic for predicting rainfall as stated by other researchers was justifiable. The advantage of fuzzy inference modeling can reflect expert knowledge and yield results with precision and accuracy. In fuzzy rule basics, knowledge acquisition is the main concern for building an expert system. Knowledge in the form of IF-THEN rules can be provided by experts or can be extracted from data. Each rule has an antecedent part and a consequent part. The antecedent part is the collection of conditions connected by AND, OR, NOT logic operators and the consequent part represents its action (Pant and Ashwagosh [8]). In a fuzzy inference engine, the truth-value for the premise of each rule is computed and applied to the conclusion part of each rule. This result is one fuzzy subset being assigned to each output variable for each rule. For composite rules, usually, min-max inference technique is used.
Defuzzification is used to convert fuzzy output sets to a crisp value. The widely used methods for defuzzification are center of gravity and mean of maxima.
Generating production rules for fuzzy inference modeling is cumbersome if they are not derived as they are being perceived by an expert. Production rules have the form:
 (1)
(1)
 (2)
(2)
Here X, Y represent two antecedent variables (the conditional part of the production rule, like TP and WS as explained above), and Z is the variable yielding the consequent part of the production rule. A1, A2, B1, B2, C1, C2 are the linguistic and vague expressions with ambiguities. Focusing this idea of production rule, an example for such production rule that can be employed in the present research is shown as:
 (3)
(3)
Equation (3) shows the qualitative form of explanation, such as very high, lower and moderate, which are all fuzzy in nature. These are explained linguistically without specific quantity or as a crisp value. The relationship of the variables between antecedent and consequent parts represents a production rule in Equation (3) based on valid logic. In the complex reality of the world, it is usually not easy to construct rules due to the limitations of manipulation and verbalization of experts, Abe and MingShong [9]. This method is termed as the Fuzzy Adaptive System (FAS).
A brief discussion of principles of reliability analysis as related to prediction of rainfall is discussed in the paper.
A large set of data for rainfall have been collected for various years from several sources as various locations. These are—AAMU 2004, WATARS 2004, BRAGG 2004, AAMU 2005, WATARS 2005 and BRAGG 2005. It has been established that there are mainly two parameters— Relative Humidity (RH) and Humidity Increase (HI) after the occurrence of rainfall. Hence, these two variables are the main random variables (RV) in this study. Since the data set is large, it can be reasonably assumed, from central limit theorem, that both RH and HI follow normal distribution. Normal distribution is a 2-parameter distribution as N(µ, σ), where µ is mean value of the random variable and σ is standard deviation of the variable under consideration.
2. Definitions
2.1. Fuzzy Set
Fuzzy sets are collection of objects with the same properties, and in crisp sets the objects either belong to the set or do not. In practice, the characteristic value for an object belonging to the considered set is coded as 1 and if it is outside the set then the coding is 0. In crisp sets, there is no ambiguity or vagueness about each object belongs to the considered set. On the other hand, in daily life humans are always confronted with objects that may be similar to one other with quite different properties. Therefore uncertainty always arises concerning the assessment of membership values 0 or 1. Logically, of course, some of the similar objects may partially belong to the same set, therefore, an ambiguity emerges in the decision of belonging or not. In order to alleviate such situations [10] generalized the crisp set membership degree as having any value continuously between 0 and 1. Fuzzy sets are a generalization of conventional set theory. The basic idea of fuzzy sets is easy to grasp. An object with membership function 1 belongs to the set with no doubt and those with 0 membership functions again absolutely do not belong to the set, but objects with intermediate membership functions partially belong to the same set. The greater the membership function, the more the object belongs to the set [11].
The membership function of a fuzzy set is a generalization of the indicator function in classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy truth represents membership in vaguely defined sets, not likelihood of some event or condition.
For the universe Χ and given the membership-degree function  the fuzzy set is defined as:
the fuzzy set is defined as:
 (4)
(4)
The following holds good for the functional values of the membership function 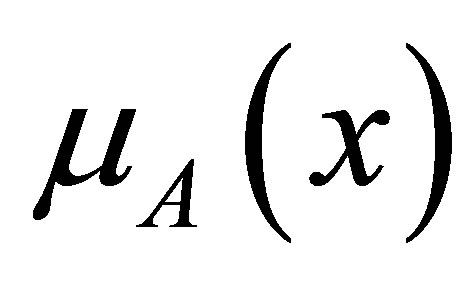
 (5)
(5)
 (6)
(6)
2.2. Fuzzy Levels
Range between the minimum (Min) and maximum (Max) value of any fuzzy variable is divided into suitable numbers which are denoted in ascending order starting from the minimum (Min) to maximum (Max) value of a fuzzy set. Figure 1 shows the range and the fuzzy levels for a fuzzy set of objects, in a triangular functional diagram. Here the range has been divided into five fuzzy levels which are NL, NS, ZE, PS, and PL. A fuzzy inference model consists of 3 modules. Figure 2 shows a schematic diagram of steps involved in fuzzy rule based system. Definitions and methods of calculations are presented below.
2.3. Fuzzification
As per Lee [12], fuzzification is a process which involves the following:
1) measures the values of input variables
2) performs a scale mapping that transfers the range of values of input variables into a corresponding universe of discourse,

Figure 1. Triangular functional diagram and method for calculating membership function (μ) and corresponding fuzzy levels.

Figure 2. General scheme of a fuzzy sastem.
3) performs the function that converts input data into suitable linguistic values which may be viewed as labels of fuzzy sets.
Figure 1 shows a value of a fuzzy variable x intersecting the triangles with fuzzy levels of ZE and NS and their respective membership functions  of 0.3 and 0.7. Hence, Fuzzification is the process that involves:
of 0.3 and 0.7. Hence, Fuzzification is the process that involves:
1) inputting the value of the fuzzy variable in the universe of discourse
2) obtaining the intersecting points on the arms of the triangles to calculate the fuzzy levels, and
3) obtaining the corresponding membership functions .
.
2.4. Min-Max Composition
From Figure 1, it is observed that one fuzzy variable (x) yields two membership functions (0.3 and 0.7) and their respective fuzzy levels are NS and ZE. Hence, if there are two fuzzy variables in the antecedent part, an increase in wind speed and a decrease in temperature when compared between the ith day and (i − 1)th day, hereafter denoted as WS and TP, respectively as in Equations (7) and (8) below, there will be four membership functions and four respective fuzzy levels obtained after fuzzification. The mathematical method followed by fuzzification is termed as “min-max composition”. Considering WS and TP as the two fuzzy variable inputs and rainfall, hereafter denoted as RF as the output in each of the production rules:
 (7)
(7)
 (8)
(8)
Fuzzifying any of these production rules will yield fuzzy levels and membership functions as shown in Figure 3. Here the values of WS and TP are the two fuzzy variables representing the antecedent part of a production rule yielding RF as its consequence that is shown inside Figure 3. Suppose a value of WS yields the membership function values of 0.2 and 0.8 belonging to the fuzzy levels of ZE and PS, respectively. Similarly, TP, another fuzzy variable in the antecedent part, yields membership functions values of 0.3 and 0.7 for the fuzzy levels of ZE and NS, respectively. Inferring fuzzy level for RF is NS which is shown in the production rule table of Figure 3. The following equation holds good:
IF WS is ZE and TP is NS THEN RF is NS (9)
Figure 3 shows that a value of membership function µ for WS equals 0.2 with its fuzzy level of ZE. This figure further shows another value of membership function µ for TP equals 0.7 with its fuzzy level of NS. A value of membership function for RF is taken to be 0.2 as it is the minimum value of µ between 0.2 and 0.7. A similar mathematical approach for the same fuzzy variables of ZE for 3 other production rules inside the table are presented for RF in Figure 3. Hence, the three minimum values 0.7, 0.2, and 0.3 for the same fuzzy levels of ZE are obtained. Finally, the maximum value 0.7 is taken out of the three minimum values of 0.7, 0.2, and 0.3 for the next step of the calculation process for defuzzification. Let us give an example to show the generalized form of the equation for min-max composition. Considering two equations for the four production rules presented in the table written here as follows:

Figure 3. Triangular functional diagram and method for calculating membership functions (μ) and corresponding fuzzy levels.
IF WS is LW1 and TP is LT1 then RF is ZE (10)
IF WS is LW2 and TP is LT2 then RF is ZE(11)
Equations (10) and (11) have the same fuzzy levels of ZE for RF. Hence, the general form of the equation for calculating the membership function  having the same fuzzy levels ZE for the consequent part can be shown as:
having the same fuzzy levels ZE for the consequent part can be shown as:
 (12)
(12)
Here,  is the membership function for RF for fuzzy level ZE,
is the membership function for RF for fuzzy level ZE,  is the fuzzy level for WS,
is the fuzzy level for WS,  is the fuzzy level for TP, and
is the fuzzy level for TP, and  indicates selecting the minimum value of membership function out of
indicates selecting the minimum value of membership function out of  and
and .
.  indicates selecting the maximum value of the calculated minimum membership function values. i is the number of production rules having the same fuzzy levels (here it is ZE). Equation (12) is valid only when i > 1.
indicates selecting the maximum value of the calculated minimum membership function values. i is the number of production rules having the same fuzzy levels (here it is ZE). Equation (12) is valid only when i > 1.
If the fuzzy levels of RF are not the same, then the membership functions of RF can be calculated by the following equation:
 (13)
(13)
Here, LV, the abbreviation for fuzzy level for RF, is different for various production rules. In these cases, only the minimum value of the membership functions between  and
and  is considered.
is considered.
2.5. Defuzzification
Defuzzification is the calculation method to yield the quantified value for the consequent part of a fuzzy statement described by production rule. Defuzzification performs the following functions:
1) a scale mapping which converts the range of values of output variables into corresponding universe of discourse, and
2) yields a non-fuzzy control action from an inferred fuzzy control action.
Figure 4 illustrates the mathematical procedure followed to calculate the center of gravity for the defuzzification method. The following are the possible cases:
Case 1. fuzzy levels of the inference part of production rules belong to NL and NS with their corresponding values of membership functions
Case 2. fuzzy levels of the inference part of production rules are in the region from NS to PS range with their corresponding values of membership functions , and
, and
Case 3. fuzzy levels of the inference part of production rules belong to PS and PL with their corresponding values of membership functions
Considering Figure 4(a) as a description of the mathematical procedure for calculating center of gravity for
 (a)
(a) (b)
(b) (c)
(c)
Figure 4. (a) Calculation method for defuzzification if the fuzzy levels for inference part of the rule table belong to NL and NS; (b) Calculation method for defuzzification if the fuzzy levels for inference part of the rule table are between NS to PS; (c) Calculation method for defuzzification if the fuzzy levels for inference part of the rule table belong to PS to PL.
Case 1, the point of intersections may be defined as ,
,  ,
,  , P4(X4, Y4) and
, P4(X4, Y4) and . Let the co-ordinate of center of gravity for the area bounded by the above five co-ordinates be
. Let the co-ordinate of center of gravity for the area bounded by the above five co-ordinates be . There are two triangles, one which can be shown by the co-ordinates
. There are two triangles, one which can be shown by the co-ordinates , P2(X1, Y2) and
, P2(X1, Y2) and ; and the other triangle can be shown by the co-ordinates P1(X1, 0),
; and the other triangle can be shown by the co-ordinates P1(X1, 0),  and P5(X5, 0).
and P5(X5, 0).
Now, the average of X values in triangle formed by ,
,  , and
, and  is
is
 (14)
(14)
and the Y value in the same triangle formed by P1(X1, 0),  , and
, and  is
is
 (15)
(15)
Similarly, X value in triangle formed by ,
,  and
and  is
is
 (16)
(16)
and the Y value in the same triangle formed by P1(X1, 0),  and
and  is
is
 (17)
(17)
Area formed by ,
, 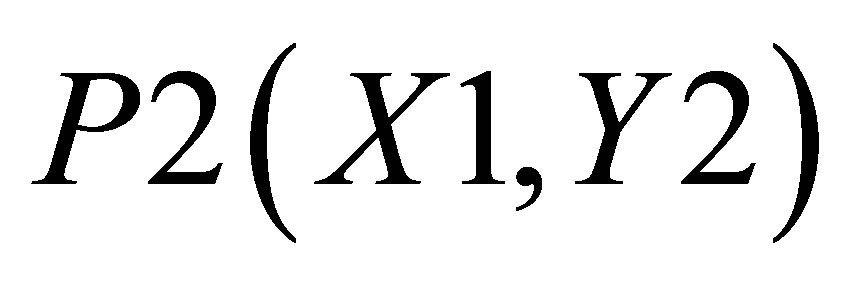 , and P3(X3, Y3) is
, and P3(X3, Y3) is
 (18)
(18)
Similarly, area formed by , P4(X4, Y4)and
, P4(X4, Y4)and  is
is
 (19)
(19)
Therefore, (20)
(20)
and the area covered by ,
,  , and
, and  is
is
 (21)
(21)
and the area covered by ,
,  and
and  is
is
 (22)
(22)
Therefore, the co-ordinate for center of gravity is
 (23)
(23)
and  (24)
(24)
Considering Figure 4(b) as describing the mathematical procedure for calculating the center of gravity for Case 2, the point of intersections may be defined as ,
,  ,
,  ,
,  ,
,  and
and . Let the co-ordinate of the center of gravity of the area bounded by the above five co-ordinates represented by thick lines be
. Let the co-ordinate of the center of gravity of the area bounded by the above five co-ordinates represented by thick lines be . Let us consider that total area under the thick lines is consisting of three small triangles which are as follows:
. Let us consider that total area under the thick lines is consisting of three small triangles which are as follows:
triangle 1 which is formed by the co-ordinates (P0, P1, and P2)triangle 2 which is formed by the co-ordinates (P0, P2, and P3), and triangle 3 which is formed by the co-ordinates (P0, P4, and P5).
The co-ordinates for triangle 1 are P0(X2, 0), P1(X1, 0), and ; triangle 2 consisting of P0(X2, 0),
; triangle 2 consisting of P0(X2, 0), 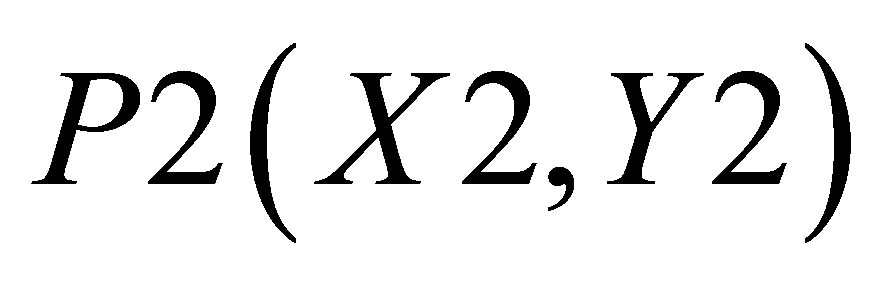 and
and ; and triangle 3 shown with the co-ordinates
; and triangle 3 shown with the co-ordinates ,
,  and
and .
.
Now, the average of X value in triangle formed by ,
,  , and
, and  is
is
 (25)
(25)
and the Y value in the same triangle formed by P0(X2, 0),  , and
, and  is
is
 (26)
(26)
Similarly, X value in triangle formed by ,
,  and
and  is
is
 (27)
(27)
and the Y value in the same triangle formed by P0(X2, 0),  and
and  is
is
 (28)
(28)
Similarly, X value in triangle formed by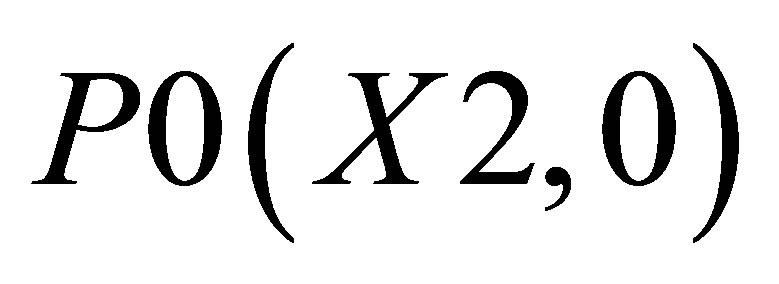 ,
,  and
and  is
is
 (29)
(29)
and the Y value in the same triangle formed by P0(X2, 0),  and
and  is
is
 (30)
(30)
Area formed by ,
,  , and P0(X2, Y2) is
, and P0(X2, Y2) is
 (31)
(31)
Similarly, area formed by ,
,  and
and  is
is
 (32)
(32)
Similarly, area formed by ,
,  and
and  is
is
 (33)
(33)
Hence,
 (34)
(34)
area covered by ,
,  , and P2(X2, Y2) is
, and P2(X2, Y2) is
 (35)
(35)
area covered by ,
,  and P3(X3, Y3) is
and P3(X3, Y3) is
 (36)
(36)
and area covered by , P4(X4, Y4) and P5(X5, 0) is
, P4(X4, Y4) and P5(X5, 0) is
 (37)
(37)
Therefore, the co-ordinate for center of gravity is
 (38)
(38)
and
 (39)
(39)
Considering Figure 4(c) for describing the mathematical procedure for calculating the center of gravity for Case 3, the point of intersections may be defined as ,
, 
 , P4(X4, Y4) and
, P4(X4, Y4) and . Let the co-ordinate of the center of gravity of the area bounded by the above five co-ordinates represented by thick lines be
. Let the co-ordinate of the center of gravity of the area bounded by the above five co-ordinates represented by thick lines be . There are two triangles one of which can be shown by the co-ordinates
. There are two triangles one of which can be shown by the co-ordinates ,
,  and P5(X4, 0)and the other triangle can be shown with the co-ordinates P3(X3, Y3), P4(X4, Y4) and
and P5(X4, 0)and the other triangle can be shown with the co-ordinates P3(X3, Y3), P4(X4, Y4) and .
.
Now, the average of X value in triangle formed by ,
,  and
and  is
is
 (40)
(40)
and the Y value in the same triangle formed by P1(X1, 0),  and
and  is
is
 (41)
(41)
Similarly, X value in triangle formed by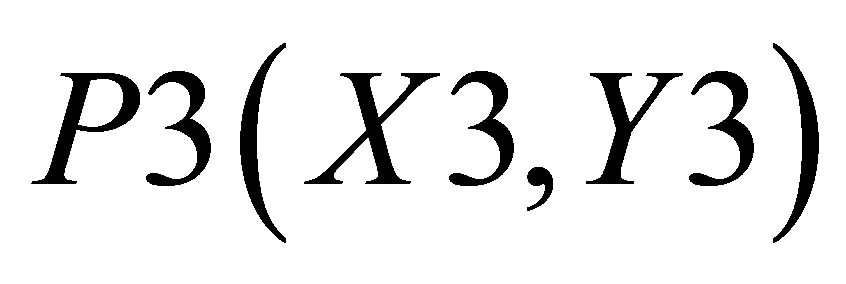 ,
,  and
and  is
is
 (42)
(42)
and the Y value in the same triangle formed by P3(X3, Y3),  and
and  is
is
 (43)
(43)
Area formed by ,
,  and P5(X4, 0) is
and P5(X4, 0) is
 (44)
(44)
Similarly, area formed by , P4(X4, Y4) and
, P4(X4, Y4) and  is
is
 (45)
(45)
Therefore, (46)
(46)
and the area covered by ,
,  and
and  is
is
 (47)
(47)
and the area covered by ,
,  and
and  is
is
 (48)
(48)
Therefore, the co-ordinate for center of gravity is
 (49)
(49)
and  (50)
(50)
3. Study Area
This manuscript presents a fuzzy inference model for predicting RF using meteorological scan data from the United States Department of Agriculture (USDA) Soil Climate Analysis Network Station at Alabama Agricultural and Mechanical University (AAMU) campus. Meteorological data for 2003 and 2004 were collected and analyzed to determine the variables that are involved in rainfall occurrences. The Alabama Mesonet (ALMNet) has been the apex representing fourteen combinations of meteorological/soil profile stations and twelve soil profile stations distributed in 11 counties in southern Tennessee and north and central Alabama. The combination stations are also part of the USDA and Natural Resources Conservation Service (NRCS) scan network. Alabama Mesonet (ALMNet) is controlled and run by the Center for Hydrology, Soil Climatology and Remote Sensing (HSCaRS) of Alabama Agricultural and Mechanical University (AAMU).
4. Model Development
Although meteorological scan data were collected for two years, 2003 and 2004, the model was developed based on year 2004 data. These data were very well organized including soil related parameters. Data for Bragg Farm and Winford A. Thomas Agricultural Research Station (WTARS) were also collected, monthly data spread sheets were prepared, and graphs plotted to assist with pre-assessment of analysis and to generate ideas on climatic behavior.
Figure 5 shows the characteristics of rainfall for the month of August 2004 using data from the AAMU campus. Based on the observations of the graphs prepared for

Figure 5. Rainfall pattem, wind and temperature (USDA scan data from AAMU campus for August 2004).
every month during the years 2003 and 2004 for AAMU, Bragg and WTARS farms, it was apparent that a value of WS and another value of TP when compared between the ith and (i − 1)th day mostly resulted in a rainfall occurrence. Usually, the characteristic of rainfall occurrence usually takes place at the first or second day of the phenomena of increasing of wind speed and decreasing of temperature. Hence, the degree of association between WS and TP when compared between the ith and (i − 1)th day causing RF occurrences was established. Based on analysis, it was observed that a RF occurrence has a positive relation with TP and WS. The observation further revealed that the relation of RF occurrence with TP and WS reflects expert knowledge. Hence, the values of WS and TP between ith and (i − 1)th day and using them in the fuzzy inference model for the antecedent part of production rules was considered to be feasible. Figure 6 shows the fuzzy inference model structure and the steps followed to determine the time and amount of RF.
This figure has been prepared by incorporating the consideration of threshold values as described in Figure 7. In the initial step of calculation, temperature, wind speed, and Relative Humidity were converted to yield the average daily values dividing by 24 (1 day = 24 h) to produce average temperature, average wind speed and average Relative Humidity.
A preliminary analysis showed that the variables described below had a significant influence over RF occurrences:
1) Relative Humidity (RH) of the ith day
2) Humidity Increase (HI) is which is increase in Relative Humidity (RH) when compared between the ith and (i − 1)th day, and
3) Product (P) of decreasing of TP and increasing of WS.
These three variables were taken into consideration and shown in Figure 6 in the calculation process with seasonal variation as shown in tabular form in Figure 7. This variation was considered with two threshold values

Figure 6. Model structure and steps in predicting timing and amount of Rainfall (RF).
for minimum and maximum limits as indicated by A and B in Figure 7:
1) Jan 1 to Apr 31
2) May 1 to Sep 30, and
3) Oct 1 to Dec 31
The threshold values were selected based on the calculation of results of the model.
In year 2004, there were 6 days out of 132 total rainy days when the actual amount of RF was more than 50 mm. Considering the uniformity of data range, and to avoid very unusual phenomena, the highest volume of RF was considered to be 50 mm for the maximum value of predicted RF for defuzzification process (refer Figure 4). The error was calculated using the following equation:
 (51)
(51)
Here, n is the number of days of rainfall occurrences,  is actual amount of rainfall, and
is actual amount of rainfall, and  is the calculated amount of rainfall.
is the calculated amount of rainfall.
5. Results and Discussions for Fuzzy Set Theory
5.1. Selection of Variables
Fuzzy variables of WS and TP between the ith and (i − 1)th day were good choices for the development of a model for predicting RF. In reality, fuzzy inference models involve with variables which are perceived by experts as responsible for the consequence part of the production rule. This means a fuzzy inference model reflects the scenario of thinking and decision-making process by expert knowledge. The fuzzy variables were chosen following the assessment on graphs prepared on the basis of monthly data from AAMU for 2003 and 2004. Selection of variables of TP and WS between the ith and (i − 1)th day was considered for this model as a better approach. The final results indicated that the selection of these two variables was suitable for the development of the model and that they showed a good agreement when used in the antecedent part of the production rule.
5.2. Selection of Fuzzy Levels for the Inference Part of the Production Rule Table
Selection of the fuzzy levels in the inference part of the production rules is a cumbersome process by trial and error method. Twenty five (5 × 5) fuzzy variables for the inference part were shown in the table in Figure 3. A method for iterating the fuzzy variables for RF was followed in the computer program that selected the one yielding the lowest percentage of error based on Equation (51). Depending on the scenario of the system, fuzzy levels in the inference part of the production rule must have either an ascending or a descending nature. Skill and logical approachability are required for determining fuzzy variables for the consequent part with respect to the fuzzy variables in the antecedent part of the production rule. The production rule table shown in Figure 6 was the best set of fuzzy levels for RF that yielded the lowest error value of 12.35%.
5.3. Maximum Value of RF
Real RF data showed that the AAMU campus USDA Soil Climate Analysis Network weather station had only 6 occurrences of more than 50 mm RF in 2004. The maximum RF was 93 mm which is very unusual and rare for the same location. Moreover, if the actual amount of RF is considered to be more than 50 mm, the region of maximum RF [around PL of Figure 4(c)] will have unealistic and lesser density of number of data compared to

Figure 7. Threshold values and ranges of the factors for predicting RF for the improved model.
density of data in the region of NL, NS, ZE, and PS. Hence, considering the uniformity of data distribution among the ranges of NL, NS, ZE, PS, and PL the maximum value of predicted RF to be 50 mm was justifiable.
5.4. Selection of Threshold Values for Predicted Value of RF
Based on the fundamental logic of this research that a value of WS and another value of TP when compared between the ith and (i − 1)th day may result in RF, their fuzzy levels, production rules, and ranges of variables, showed dependency on three other possible factors. These factors need to be considered with their threshold values for matching the actual and calculated amount of RF. These factors are 1) average daily Relative Humidity (RH); 2) Humidity Increase (HI) between the ith and (i − 1)th day; and 3) Product (P) of TP and WS between the ith and (i − 1)th day. Figure 7 represents two boundary values (A) and (B) for RH. The zone between (A) and (B) is the range for a possible RF and the zone beyond (B) is the zone for RF regardless of any other consideration, whereas the RH of less than (A) is the zone for no RF. When the value of HI is more than 10 and it is within the boundary values of (A) and (B) then it becomes the zone for RF. The zone for the value of HI of less than 10 is again the zone for a possible RF occurrence. This possibility is further considered to occur when the value of product (P) of TP and WS is greater than 4. But if the value of P of TP and WS is less than 4, then it was considered that there would be no RF occurrence. Introducing these three threshold values with consideration of three different seasons as described in Figure 7, the model showed good agreement between the actual amount of RF and predicted value for RF. Figures 8 to 10 show the actual and predicted values of RF using 2004 scan data from the USDA Soil Climate Analysis Network Station at the AAMU campus. These figures illustrate the actual amount of RF and predicted value of RF during three different seasons as considered in this model and explained in Figure 7. The figures further show that the timeliness of the actual amount of RF and predicted value of RF almost perfectly match, but the amount of RF needs further research to yield better agreement between actual and predicted values of RF. Therefore, further research planned to develop an approach for auto-generation of the production rules by iteration method and selecting the particular production rule table that yields the lowest percentage of error.
6. Methodology for Reliability Analysis
It consists of following steps:
Step 1 - Calculate mean value  and standard deviation
and standard deviation  for each of the parameters affecting rainfall, namely, relative humidity (RH) and humidity increase (HI) from the following equations:
for each of the parameters affecting rainfall, namely, relative humidity (RH) and humidity increase (HI) from the following equations:
 (52)
(52)
Where, n = number of samples
 (53)
(53)
This step is done for all the sets of data from various sources at various locations-AAMU 2004, BRAGG 2004, WATARS 2004, AAMU 2005, BRAGG 2005 and WATARS 2005.
Step 2 - Calculate the following theoretical probabilities for RH (assuming normal distribution) from information in step 1 as follows:
 for January 1 to April 30
for January 1 to April 30
 for May 1 to September30
for May 1 to September30
 for October 1 to December 31 X represents the random variable (Relative Humidity). WherePth1 = theoretical probability for Event 1 for RH Pth2 = theoretical probability for Event 2 for RH Pth3 = theoretical probability for Event 3 for RH
for October 1 to December 31 X represents the random variable (Relative Humidity). WherePth1 = theoretical probability for Event 1 for RH Pth2 = theoretical probability for Event 2 for RH Pth3 = theoretical probability for Event 3 for RH
Step 3- Count number of samples falling in the range for each event (1-3) and calculate the corresponding experimental probabilities as follows:



Wheren1 = number of samples within the range of 70 - 85 (between January 1-April 30)
nte1 = total number of samples for event 1 (January 1- April 30)
n2 = number of samples within the range of 80 - 90 (between May 1-Sept. 30)
nte2 = total number of samples for event 2 (May 1- Sept. 30)
n3 = number of samples within the range of 75 - 90 (between October 1-December 31)
nte3 = total number of samples for event 3 = 115 (between October 1-December 31)
Step 4- Calculate the following theoretical probabilities for HI (assuming normal distribution) from information in step 1 as follows:
X represents the random variable (HI - Humidity increase)
 for January 1 to April 30
for January 1 to April 30
 for May 1 to September30
for May 1 to September30
 for October 1 to December 31 WherePth4 = theoretical probability for Event 1 - for HI Pth5 = theoretical probability for Event 2 for HI Pth6 = theoretical probability for Event 3 for HI
for October 1 to December 31 WherePth4 = theoretical probability for Event 1 - for HI Pth5 = theoretical probability for Event 2 for HI Pth6 = theoretical probability for Event 3 for HI
Step 5- Count number of samples falling in the range for each event (1-3) and calculate the corresponding experimental probabilities as follows:



Wheren4 = number of samples of HI <= 10 (between January 1-April 30)
nte4 = total number of samples for HI for event 1 (January 1-April 30)
n5 = number of samples of HI <= 10 (between May 1- Sept. 30)
nte5 = total number of samples for HI event 2 (May 1- Sept. 30)
n6 = number of samples <= 10 (between October 1- December 31)
7. Results for Reliability Analysis
Results based on the reliability analysis are given in Tables 1 and 2. These tables lists all the statistical parameters for the two random variables connected with rainfall data (“RH” and “HI”).
8. Discussion and Results
Tables 1 and 2 give statistical parameters (sample mean value, sample standard deviation and sample coefficient of variation (CV)) for relative humidity (RH) and humidity increase (HI). It is seen from these tables that the value of CV for the HI data is quite high (more than 1). CV is supposed to be less than 1 for good quality control.
Tables 3 and 4 give probabilities for RH and HI for various periods. The reason for considering these two parameters is because these are found to effect the rainfall to the maximum as discussed in this paper.Tables 3 and 4 also show the comparison between theoretical and experimental probabilities for these two variables. It can be seen from these tables that they compare reasonably well. Another point to be noted is that all the experimenttal probabilities fall within 1 standard deviation (σ) from the mean value i.e. (µ − σ and µ + σ) which represent about 63% of the uncertainty which reflects well on the data that is collected and theoretical analysis performed.
To calculate the probability of rainfall one can multiply the probabilities of the events for a particular period for RH and the same period for HI. For example for the period of January 1-April 30 (for RH values in the range of 70 - 80), the probability of rainfall is about 20%. This This number is calculated by multiplying the two probabilities considering they are independent events. Similarly, probabilities can be calculated for other ranges of RH and HI.

Table 1. Statistical Parameters for random variable (RH) connected with rainfall.

Table 2. Statistical Parameters for random variable (HI) connected with rainfall.

Table 3. Theoretical and Experimental Probabilities for Relative Humidity (RH) Connected with Rainfall.

Table 4. Theoretical and Experimental Probabilities for Humidity Increase (HI).
9. Conclusion
Selection of variables and the fundamental logic of the values TP and WS was an attempt to identify amount of RF and its time of occurrence as the consequent part of the fuzzy inference model. Introducing the idea of threshold values of a) RH of the ith day, b) HI when compared between the ith and (i − 1)th day, and c) P, product of WS and TP appeared to be an appropriate attempt for the model to match the actual RF occurrences. Iteration of the fuzzy levels with logic both for antecedent and consequent parts was found to be efficient. Further research has been planned to attain the maximum possible matches of time and amount of RF between actual occurrences and the one predicted by the model. A methodology has been developed for reliability analysis to predict rainfall.