1. Introduction
Throughout we denote the complex 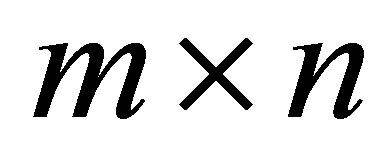 matrix space by
matrix space by . The symbols
. The symbols  and
and 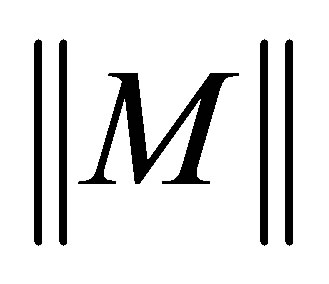 stand for the identity matrix with the appropriate size, the conjugate transpose, the inverse, and the Frobenius norm of
stand for the identity matrix with the appropriate size, the conjugate transpose, the inverse, and the Frobenius norm of , respectively.
, respectively.
The reflexive matrices have extensive applications in engineering and scientific computation. It is a very active research topic to investigate the reflexive solution to the linear matrix equation
 (1)
(1)
where  and
and  are given matrices. For instance, Cvetković-Ilić [1] and Peng et al. [2] have given the necessary and sufficient conditions for the existence and the expressions of the reflexive solutions for the matrix Equation (1) by using the structure properties of matrices in required subset of
are given matrices. For instance, Cvetković-Ilić [1] and Peng et al. [2] have given the necessary and sufficient conditions for the existence and the expressions of the reflexive solutions for the matrix Equation (1) by using the structure properties of matrices in required subset of  and the generalized singular value decomposition (GSVD); Different from [1,2], Ref. [3] has considered generalized reflexive solutions of the matrix Equation (1); in addition, Herrero and Thome [4] have found the reflexive (with respect to a generalized
and the generalized singular value decomposition (GSVD); Different from [1,2], Ref. [3] has considered generalized reflexive solutions of the matrix Equation (1); in addition, Herrero and Thome [4] have found the reflexive (with respect to a generalized —reflection matrix
—reflection matrix ) solutions of the matrix Equation (1) by the (GSVD) and the lifting technique combined with the Kronecker product.
) solutions of the matrix Equation (1) by the (GSVD) and the lifting technique combined with the Kronecker product.
2. The Reflexive Least Squares Solutions to Matrix Equation (1)
We begin this section with the following lemma, which can be deduced from [5].
Lemma 1. (Theorem 3.1 in [5]) Let the canonical correlation decomposition of matrix pair  and
and  with
with . rank
. rank , rank
, rank , rank
, rank , rank
, rank be given as
be given as


where
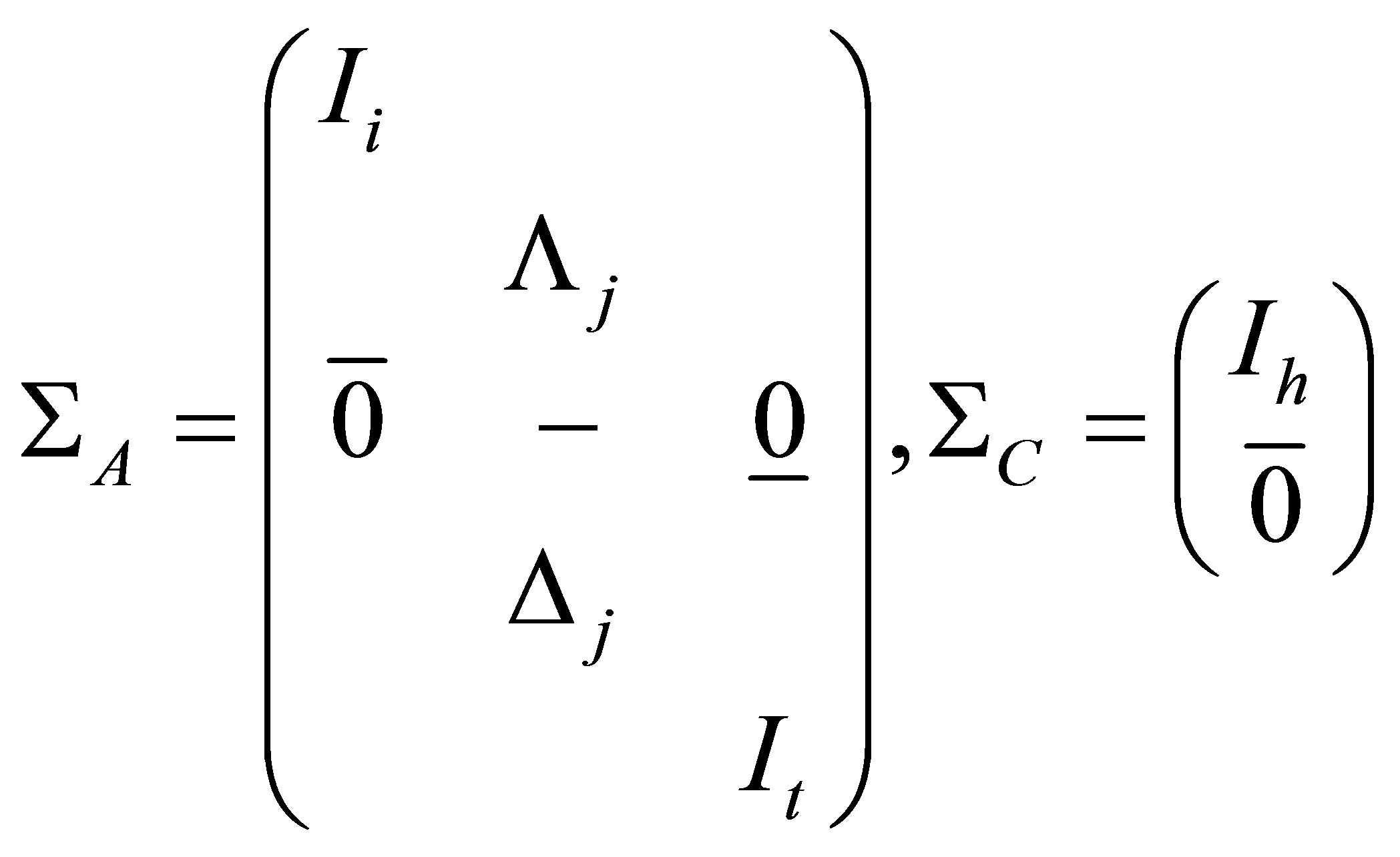
with the same row partitioning, and ,
,



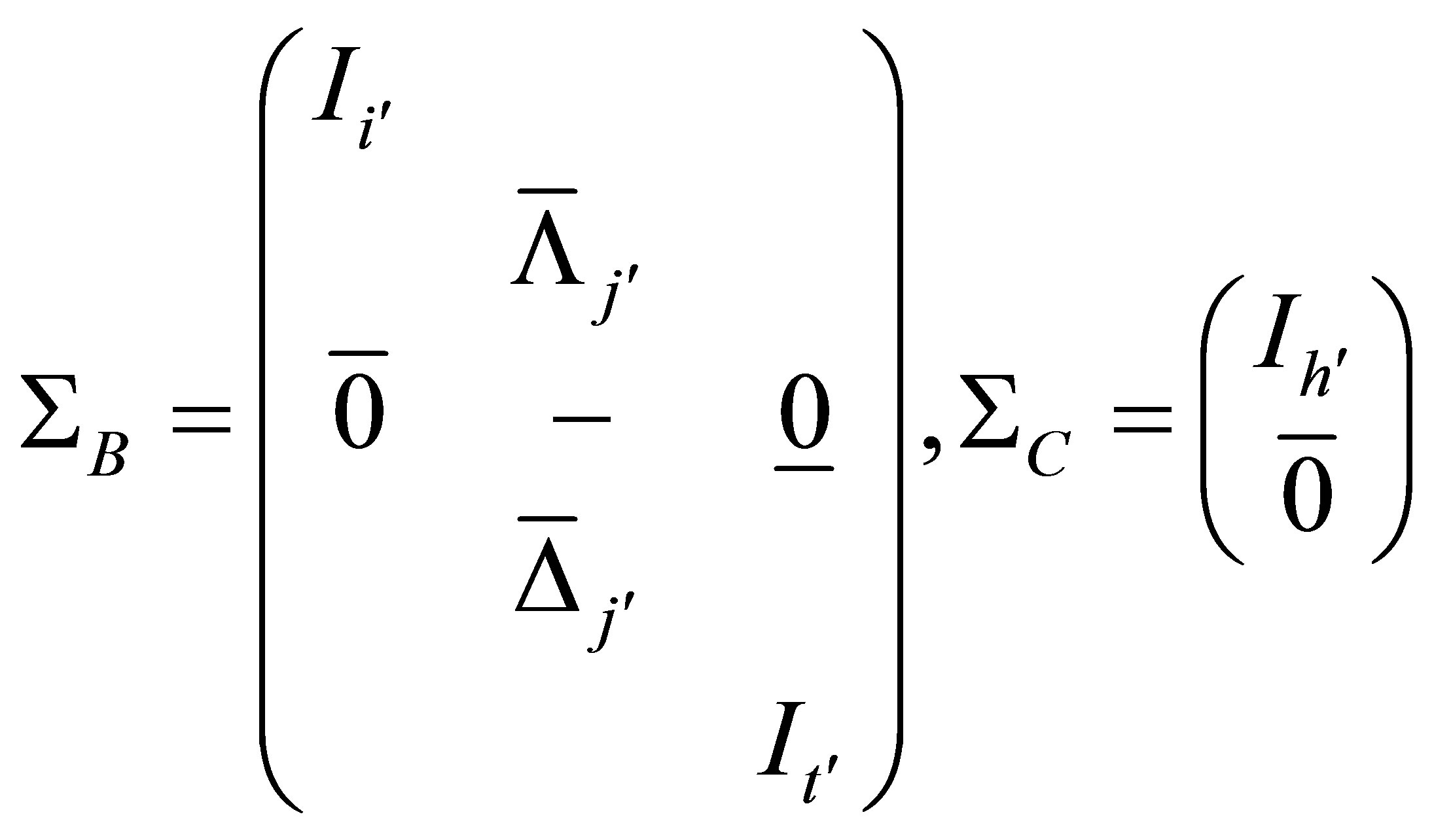
with the same row partitioning, and 



and let

Then general forms of least squares solutions  of matrix equation
of matrix equation

are as follows:
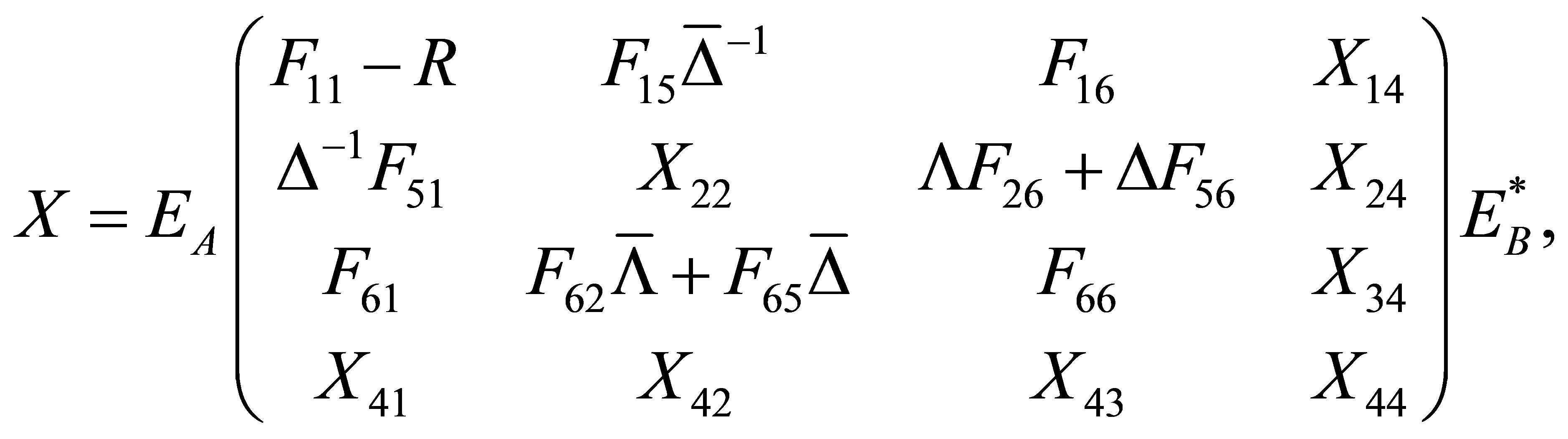

where

and 
are arbitrary matrices.
Theorem 2. Given 

 . Then the reflexive least squares solutions to the matrix Equation (1) can be expressed as
. Then the reflexive least squares solutions to the matrix Equation (1) can be expressed as
 (2)
(2)
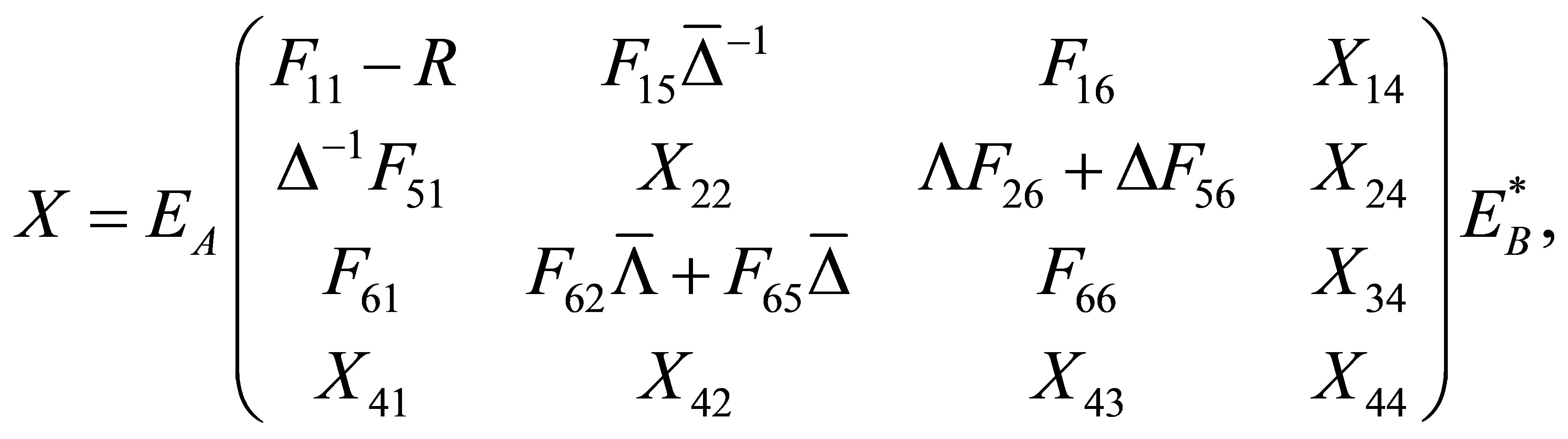

where

and 
are arbitrary matrices.
Proof. It is required to transform the constrained problem to unconstrained ones. To this end, let

be the eigenvalue decomposition of the Hermitian matrix  with unitary matrix
with unitary matrix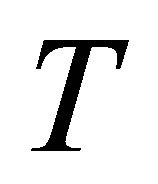 . Obviously,
. Obviously,  holds if and only if
holds if and only if
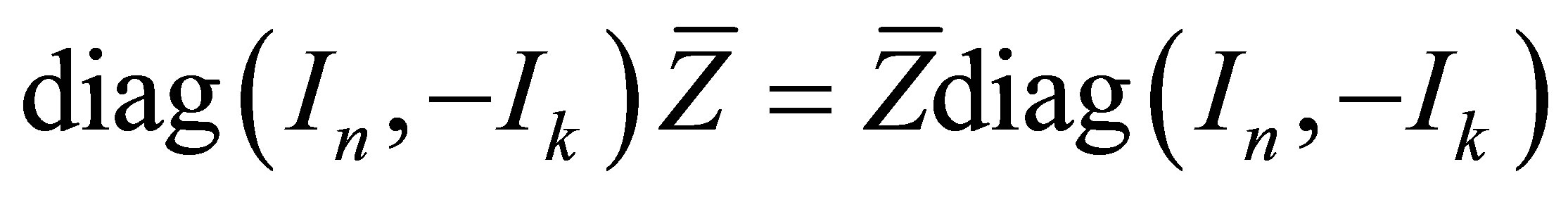 (3)
(3)
where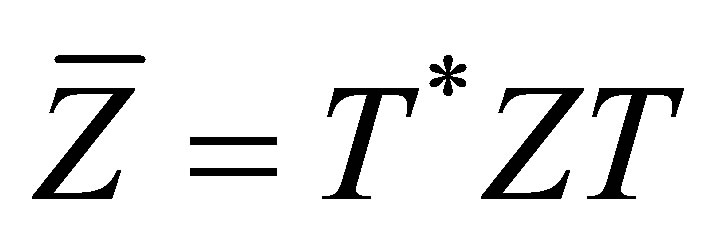 . Partitioning
. Partitioning
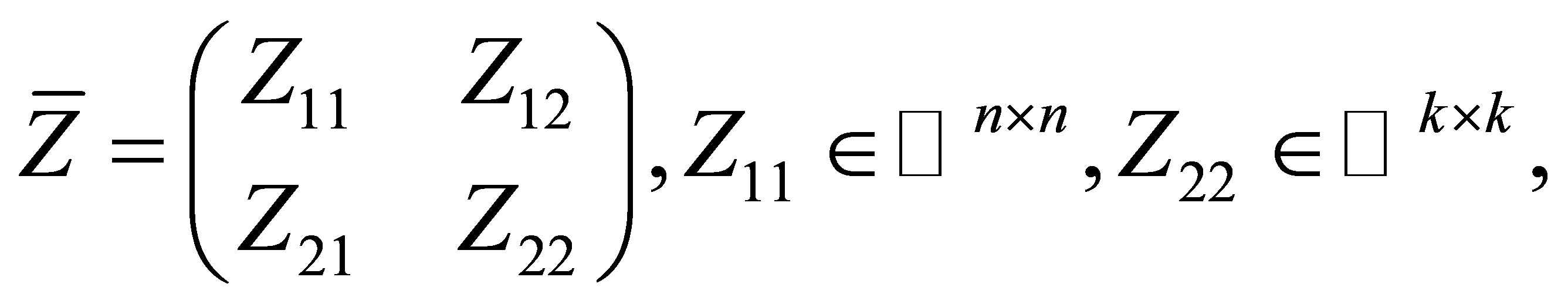
(3) is equivalent to

Therefore,
 (4)
(4)
Partition  and denote
and denote
 (5)
(5)
According to (4), (5) and the unitary invariance of Frobenius norm

Applying Lemma 2.1, we derive the reflexive least squares solutions to matrix Equation (1) with the constraint  which can be expressed as (2).
which can be expressed as (2).
3. Acknowledgements
This research was supported by the Natural Science Foundation of Hebei province (A2012403013), the Natural Science Foundation of Hebei province (A2012205028) and the Education Department Foundation of Hebei province (Z2013110).