Metric of a Slow Rotating Body with Quadrupole Moment from the Erez-Rosen Metric ()
1. Introduction
The first quadrupole solution to the Einstein field equations (EFE) was found by Erez and Rosen [1]. Some errors were found in this derivation. These were later corrected by Doroshkevich et al. [2], Winicour et al. [3] and Young and Coulter [4]. Other multipole solutions to the EFE were obtained by Quevedo [5,6], Quevedo and Mashhoon [7], and Castejón-Amenedo et al. [8]. In the first three articles, the solutions were obtained with the help of the Hoenselaers-Kinnersley-Xanthopoulos (HKX) transformations [9], while in the latter, they used the Ernst formalism [10]. These authors obtain new metrics from a given seed metric. One can include other desirable characteristics (rotation, multipole moments, etc.) to these seed metrics by means of these formalisms. Recently, Boshkayev et al. [11] obtained an approximate solution describing the interior and exterior gravitational field of a slowly rotating and slightly deformed object.
The aim of this article is to derive an appropriate analytical tractable metric for calculations in astrometry and gravitational lens theory including the quadrupole moment and rotation in a natural form. For this new rotating metric, it is not necessary for a multipolar expansion in the potential to include the multipolar terms because the seed metric already has a quadrupole term, that is to say this metric is multipolar intrinsically.
This paper is organized as follows. In Section 2, we get the weak limit of the Erez-Rosen metric. The Lewis metric is presented in Section 3. The perturbation method is discussed in Section 4. The application of this method leads to a new solution to the EFE with quadrupole moment and rotation. It is checked by means of the REDUCE software [12] that the resulting metric is solution of the EFE. In Section 5, we compare our solution with the exterior Hartle-Thorne metric [13] in order to assure that our metric has astrophysical meaning. In Section 6, we transform the obtained metric using Cartesian coordinates. Forthcoming works with this metric are discussed in Section 7.
2. Weak Limit of the Erez-Rosen Metric
The Erez-Rosen metric [3,4,14,15] represents a body with quadrupole moment. The principal axis of the quadrupole moment is chosen along the spin axis, so that gravitational radiation can be ignored. This metric is given by
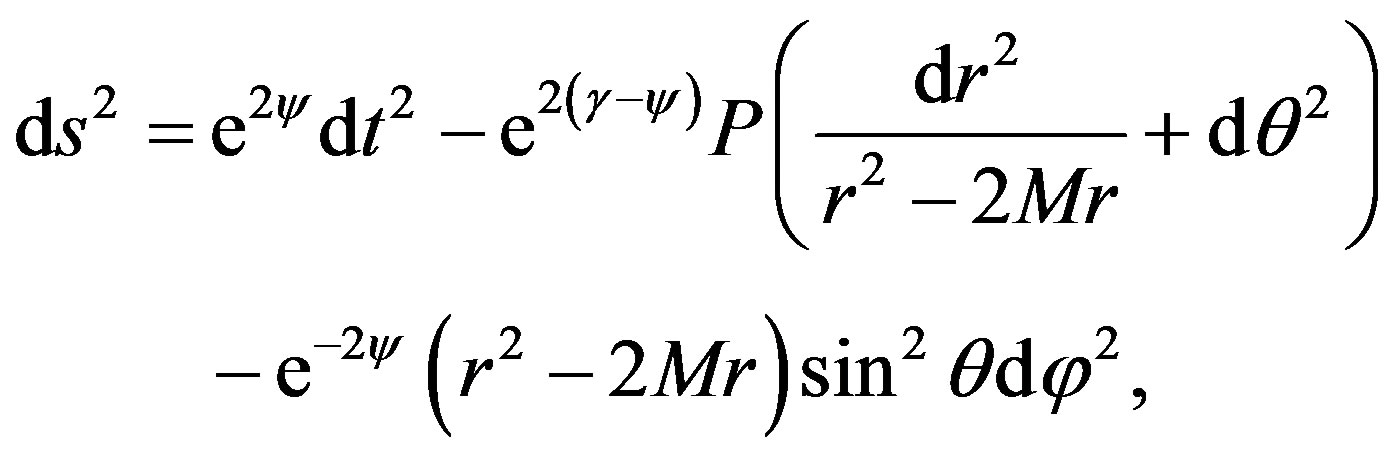 (1)
(1)
where M is the mass of the object and
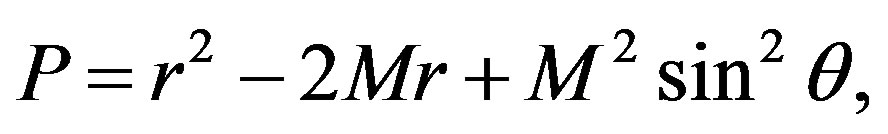
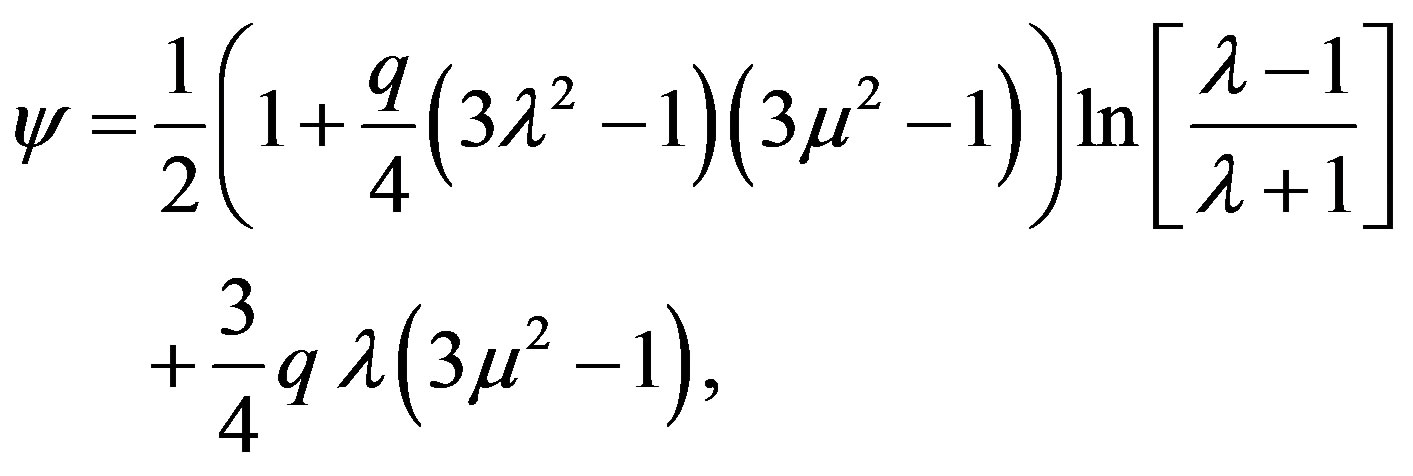
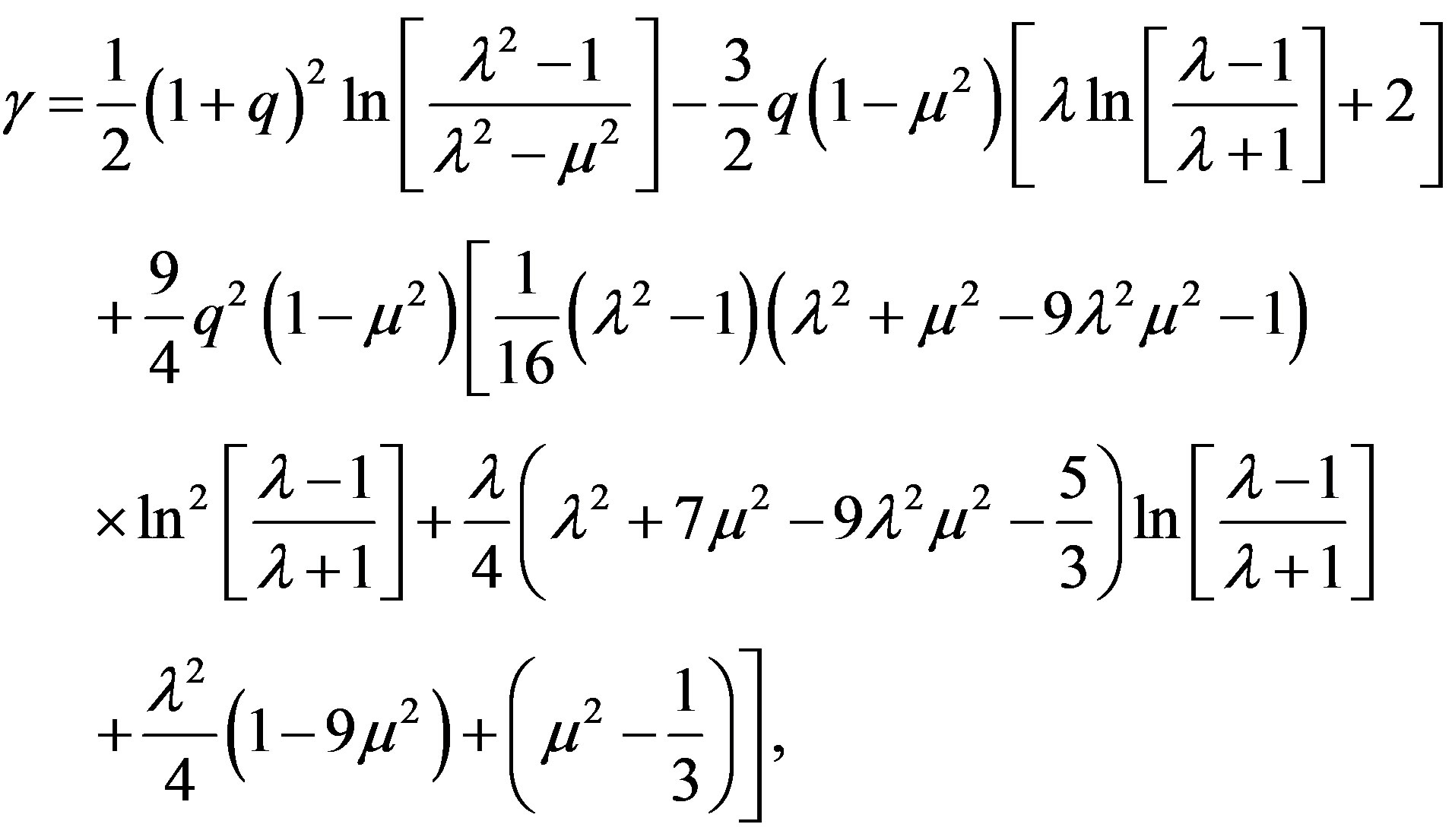
with λ = r/M - 1 and μ = cosθ. From now on, we will keep in the derivations terms up to order M2 and qM3. The approximate forms of ψ and γ are
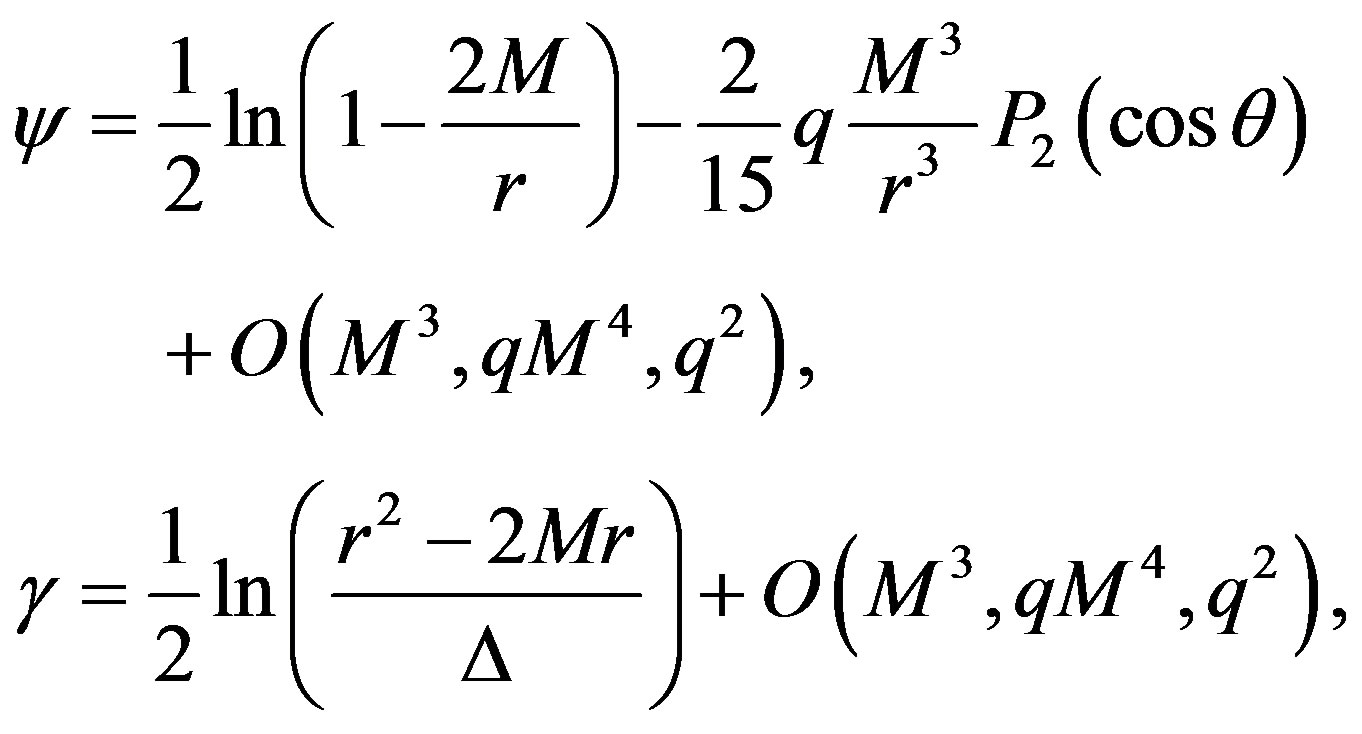
where  with Q representing the quadrupole moment, and
with Q representing the quadrupole moment, and 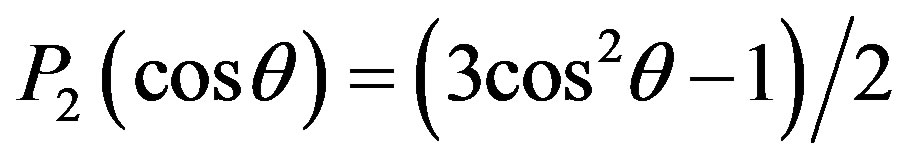 is the second Legendre polynomial.
is the second Legendre polynomial.
We define the following variables
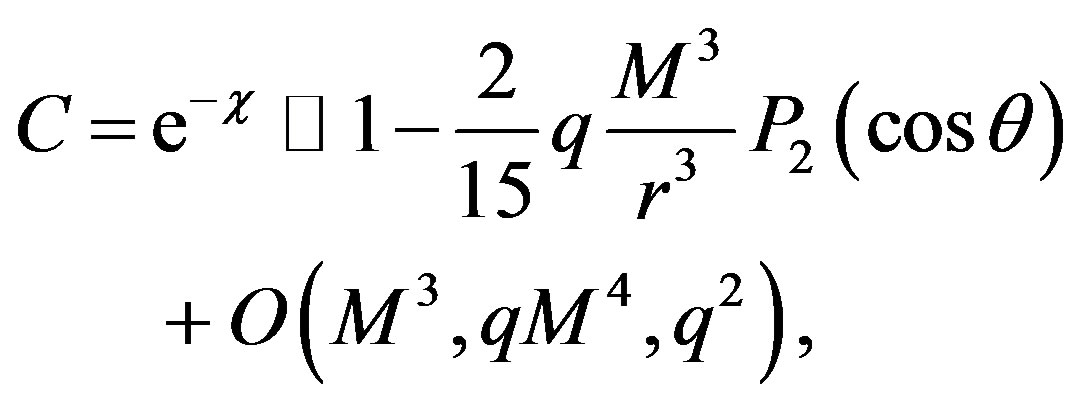 (2)
(2)

and
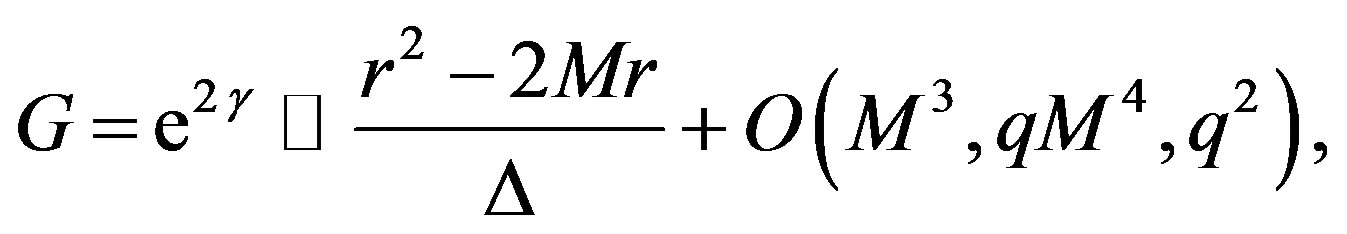
where
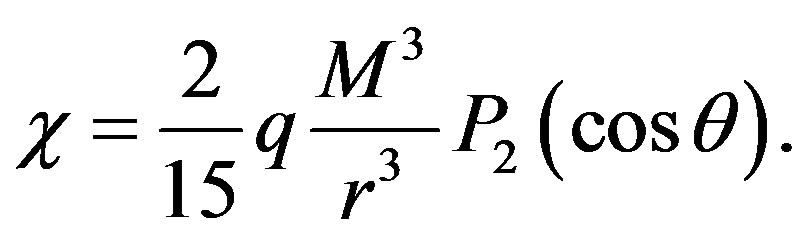
If we substitute the former definitions into (1), the metric takes the form
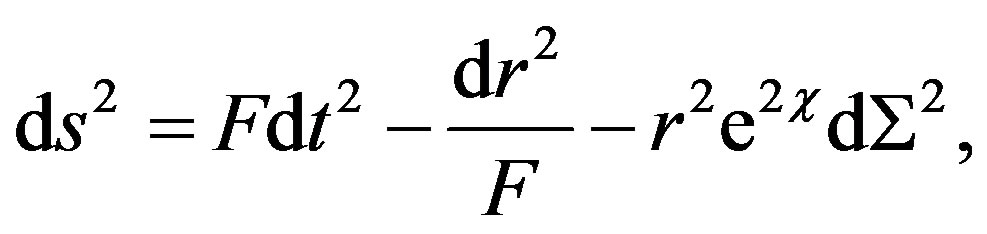 (3)
(3)
where 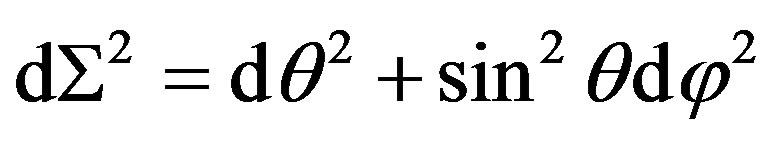 and the inverse of F is written as
and the inverse of F is written as
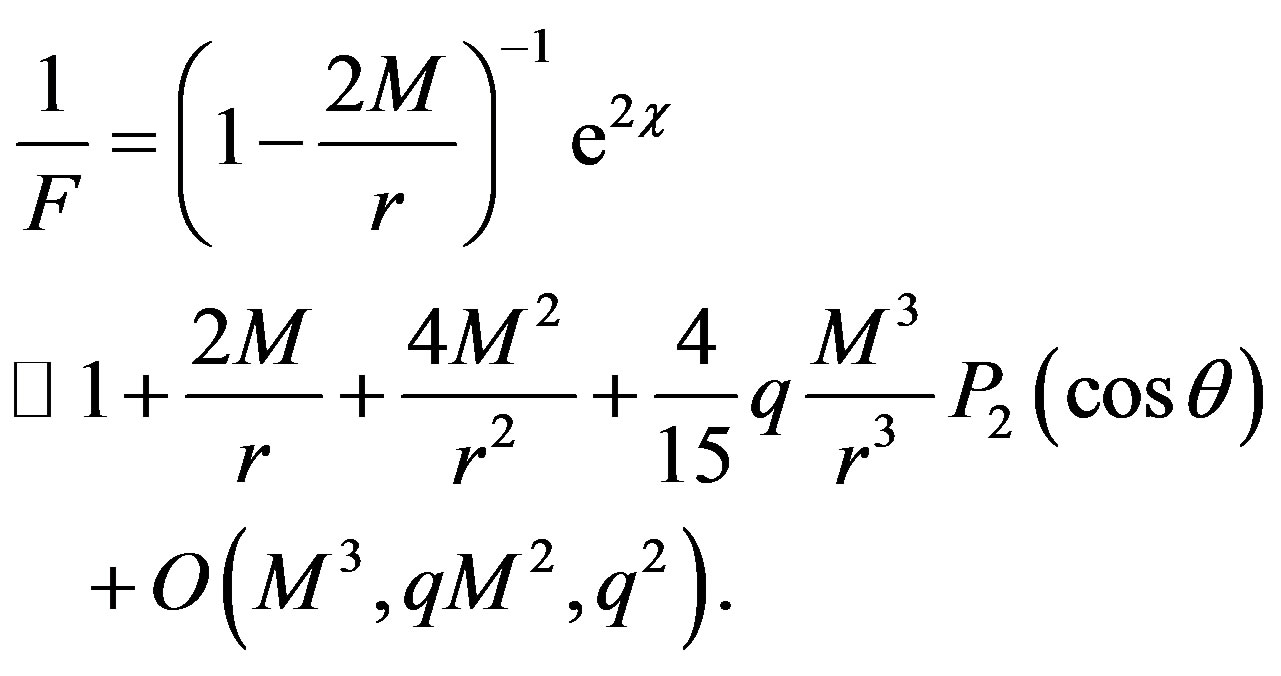
It is interesting to note that the spherical symmetry is not presented in the weak limit.
3. The Lewis Metrics
The Lewis metric is given by [14,16]
 (4)
(4)
where we have chosen the canonical coordinates x1 = ρ and x2= z, V, W, Z, μ and ν are functions of ρ and z (ρ2 = VZ + W2). Choosing μ = ν and performing the following changes of potentials.
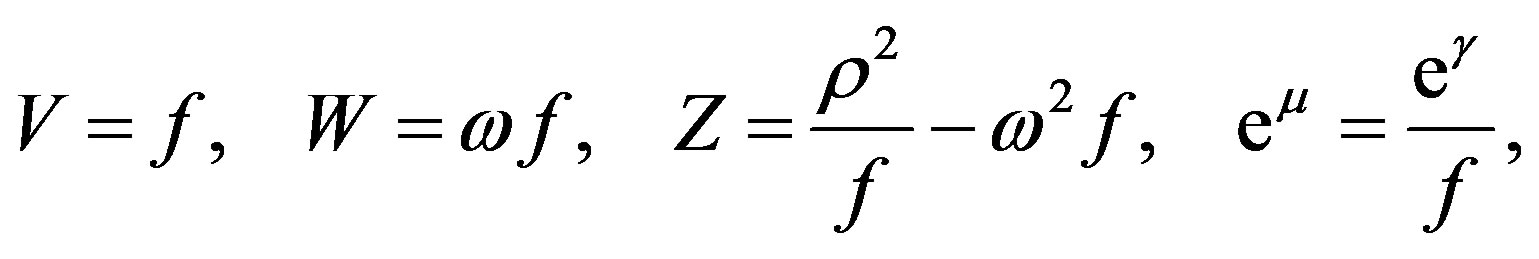
we get the Papapetrou metric
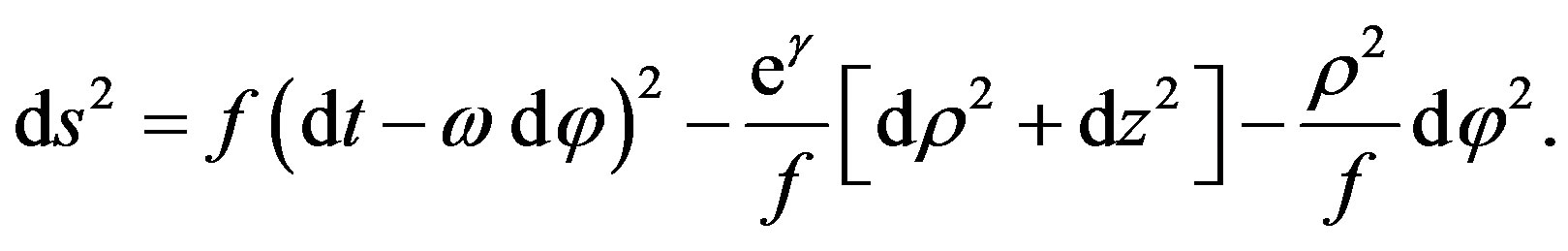 (5)
(5)
4. Perturbing the Erez-Rosen Metric
To include slow rotation into the Erez-Rosen metric we use the Lewis-Papapetrou metric (5). First of all, we choose expressions for the canonical coordinates ρ and z. For the Kerr metric [17], one particular choice is [6,18]
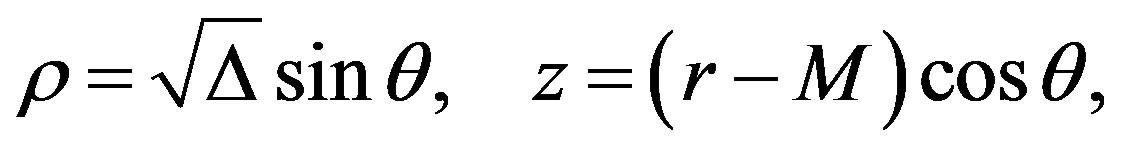 (6)
(6)
where
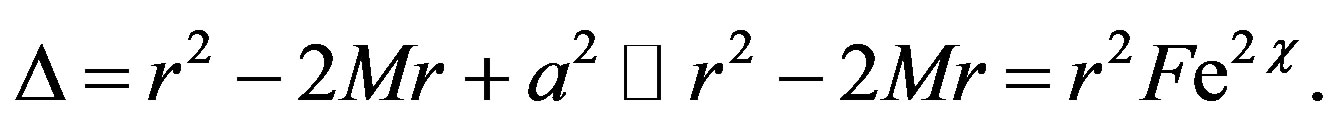
From (6) we get
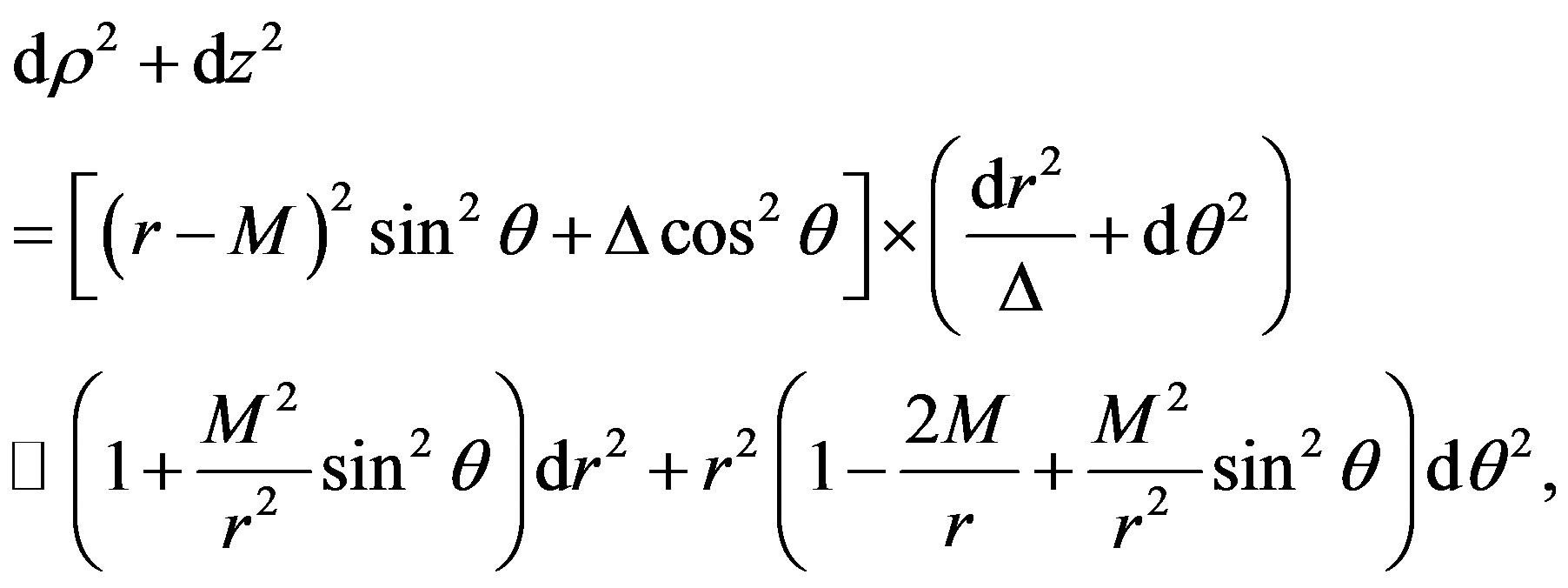 (7)
(7)
where we have expanded up to M2 order.
Now, let us choose V = f = F and neglect the second order in ω (ω2 ≈ 0, W2 ≈ 0). Then, we have
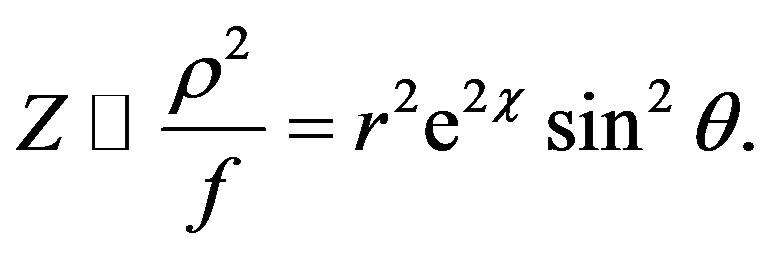
If we choose
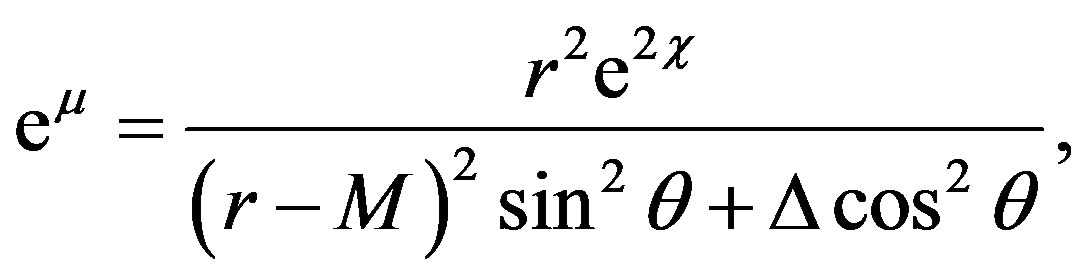
the term (7) becomes
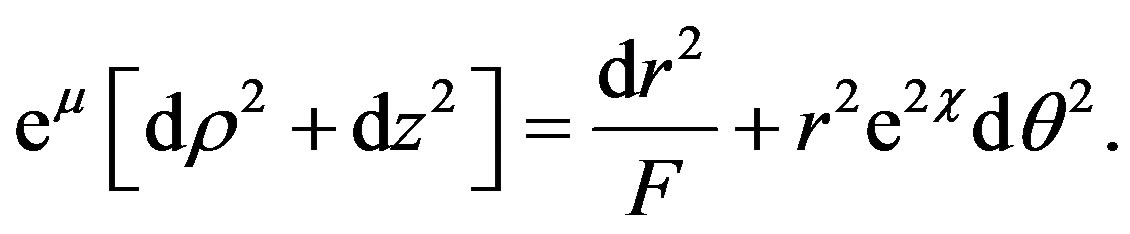
This term appears in the approximate Erez-Rosen metric (3). From (5), let us propose the following metric
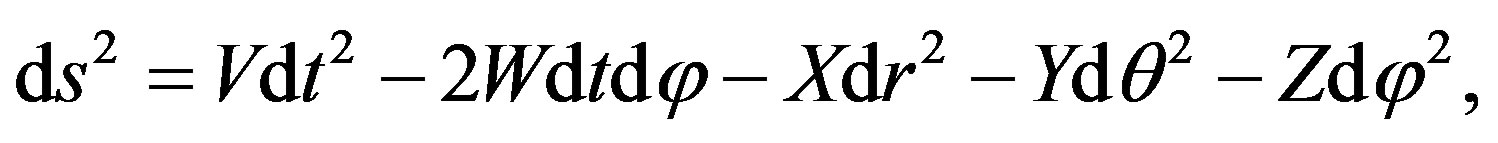 (8)
(8)
where X = 1/V, Y = r2e2χ, and Z = r2e2χsin2θ.
We see that to obtain a slowly rotating version of the metric (3) the only potential we have to find is W. Then, the EFE must be solved:

where Rij (i, j = 0, 1, 2, 3) are the Ricci tensor components and R is the curvature scalar.
Fortunately, the Ricci tensor components R00, R11, R12, R22, R33 and the curvature scalar Rs depend upon the potentials V, X, Y, Z and not on W. Therefore, these components vanish (see Appendix). The only remaining equation we have to solve is R03 = 0, because it depends upon W. The equation for this component up to the order O(M3, a2, qM4, q2) is

The solution for this equation is
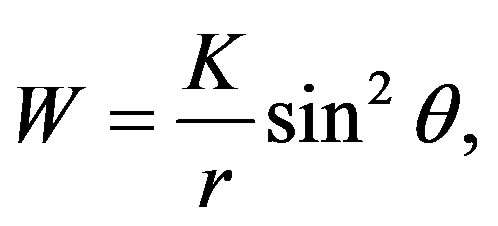
where K is a constant that we have to find. This constant can be found from the Lense-Thirring metric which can be obtained from the Kerr metric, i.e.
 (9)
(9)
where J = Ma is the angular momentum and a is the rotation parameter.
Comparing the second term of the latter metric with the corresponding of the metric (8), i.e. W, we note that K= -2J = -2Ma.
Then, the new rotating metric with quadrupole moment written in standard form [19] in spherical coordinates is
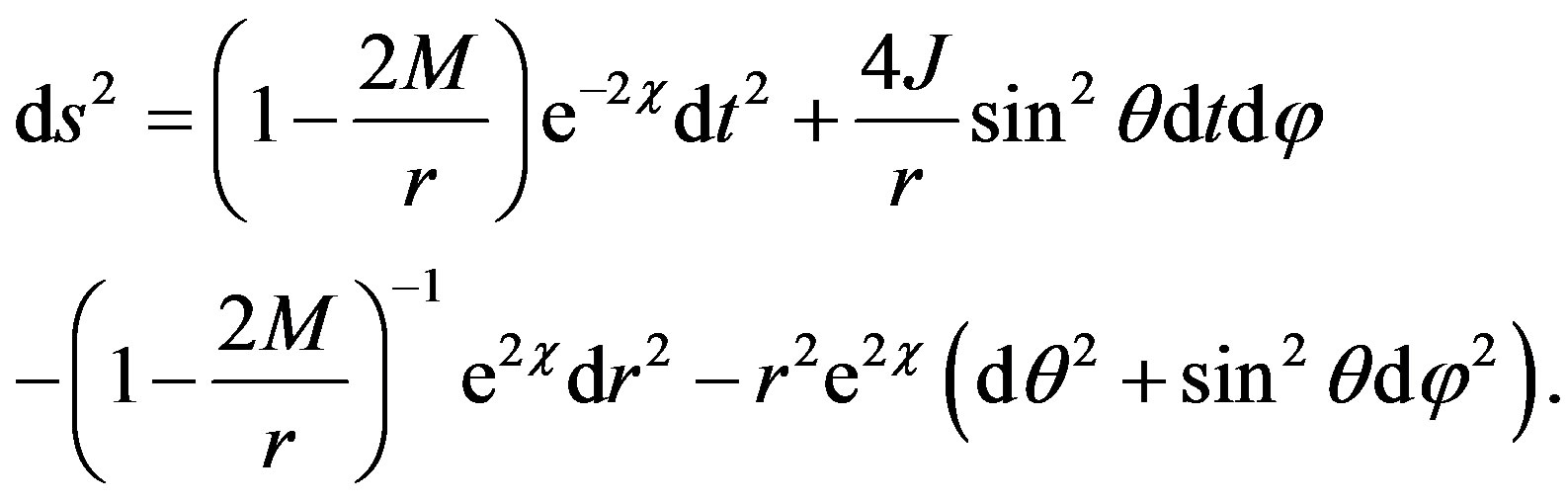 (10)
(10)
We verified that the metric (10) is indeed a solution of the EFE using REDUCE [12] up to the order O(a2, qM4, q2). Hence, one does not need to expand the term 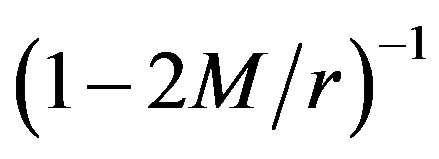 in a Taylor series.
in a Taylor series.
5. Comparison with the Exterior Hartle-Thorne Metric
In order to establish whether our metric does really represent the gravitational field of an astrophysical object, one should show that it is possible to construct an interior solution, which can appropriately be matched with the exterior solution. For this purpose, we employ the exterior Hartle-Thorne metric [13,20], which is given by
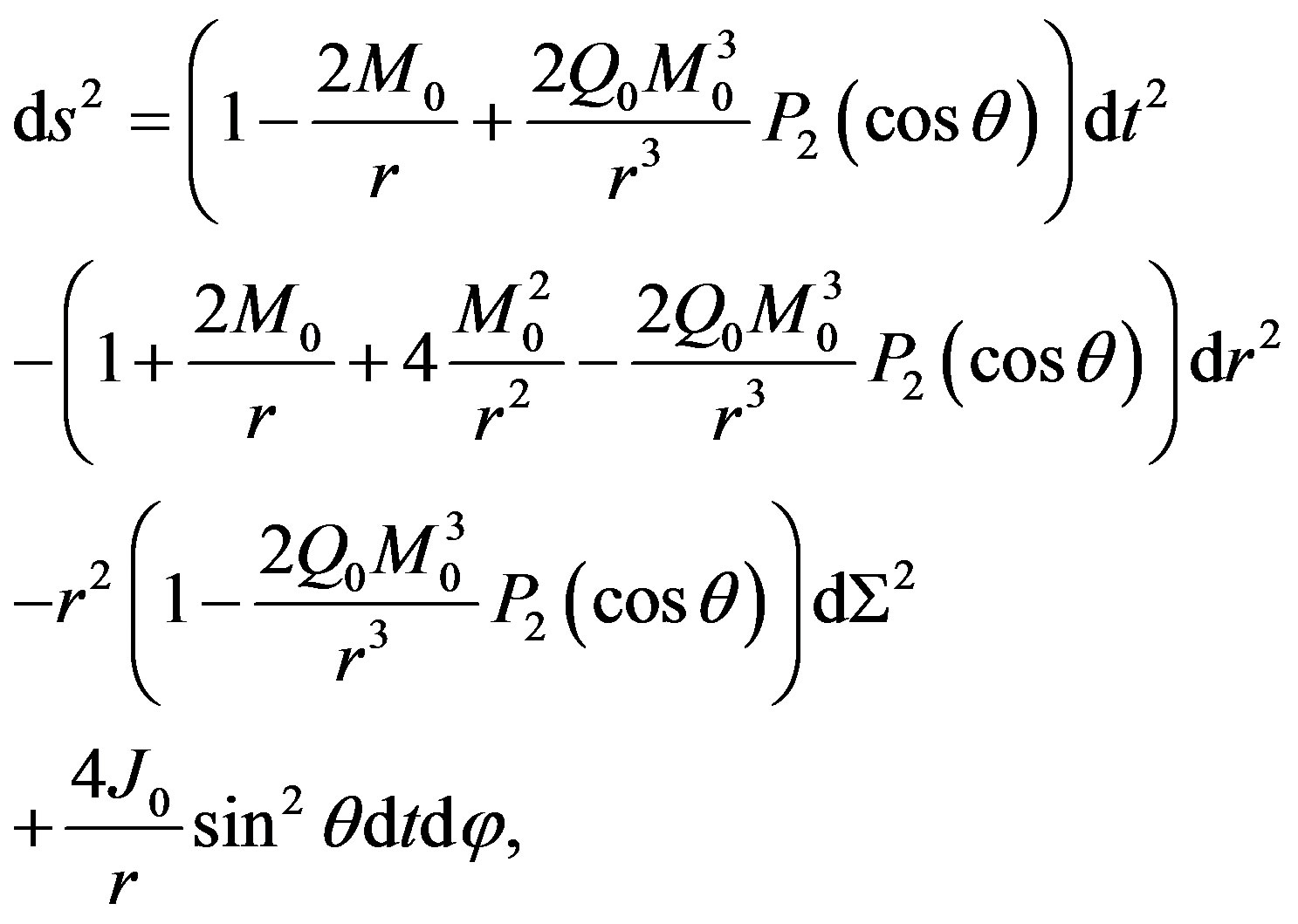 (11)
(11)
where M0, J0, and Q0 are related with the total mass, angular momentum, and mass quadrupole moment of the rotating object, respectively.
Now, comparing the exterior Hartle-Thorne metric with our expression (10), it can easily be seen that upon defining
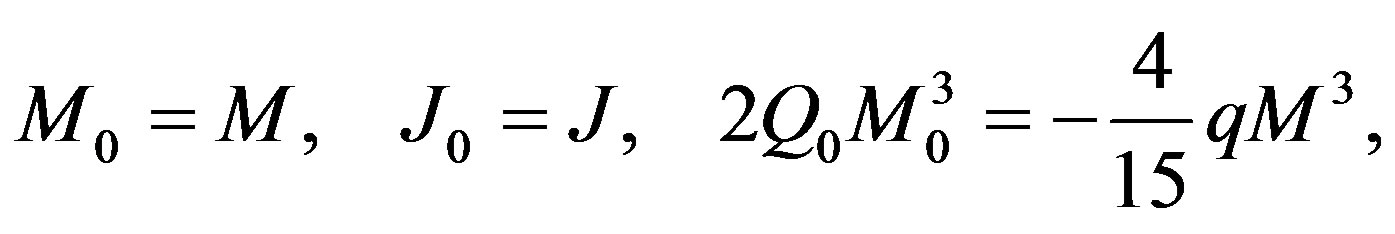 (12)
(12)
both metrics coincide up to the order O(M3, a2, qM4, q2). Our approximate expression for the Hartle-Thorne metric (11) was obtained by means of a REDUCE program using the expressions from Abramowicz et al. [21]. We compared these results with the approximate expression given by Boshkayev et al. [11] and found that they have an extra term of order O(qM4), which we neglected, because it is beyond the order we are working with. Additional differences are that our metric parameters (M, J = Ma, qM3) are distinct and our expressions (12) are simpler than those of Boshkayev et al. [11].
6. The Transformation of the Metric
In some cases, the metric (10) has to be transform from spherical (r, θ, φ) into Cartesian coordinates (x, y, z). For example, if a comparison with a post-Newtonian (PN) metric is made, we have to transform the metric (10) by using one of the following radial coordinates transformation: the harmonic or the isotropic coordinates of Schwarzschild metric. The first one is r = R + M, and the second one is r = R(1 + M/2R)2, where R is a new radial coordinate [19]. We choose the first one, then the metric (10) is transformed into
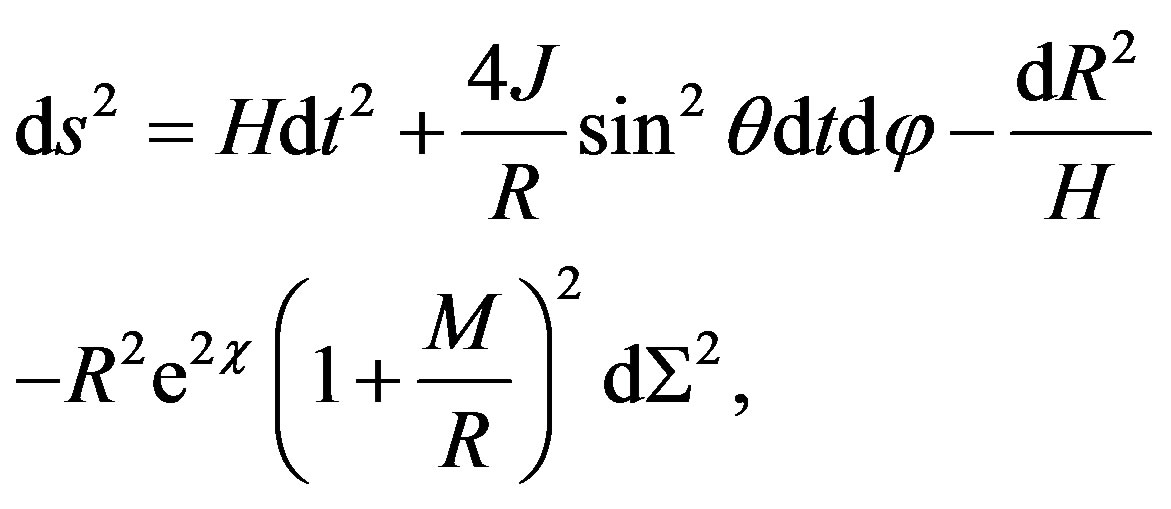 (13)
(13)
where
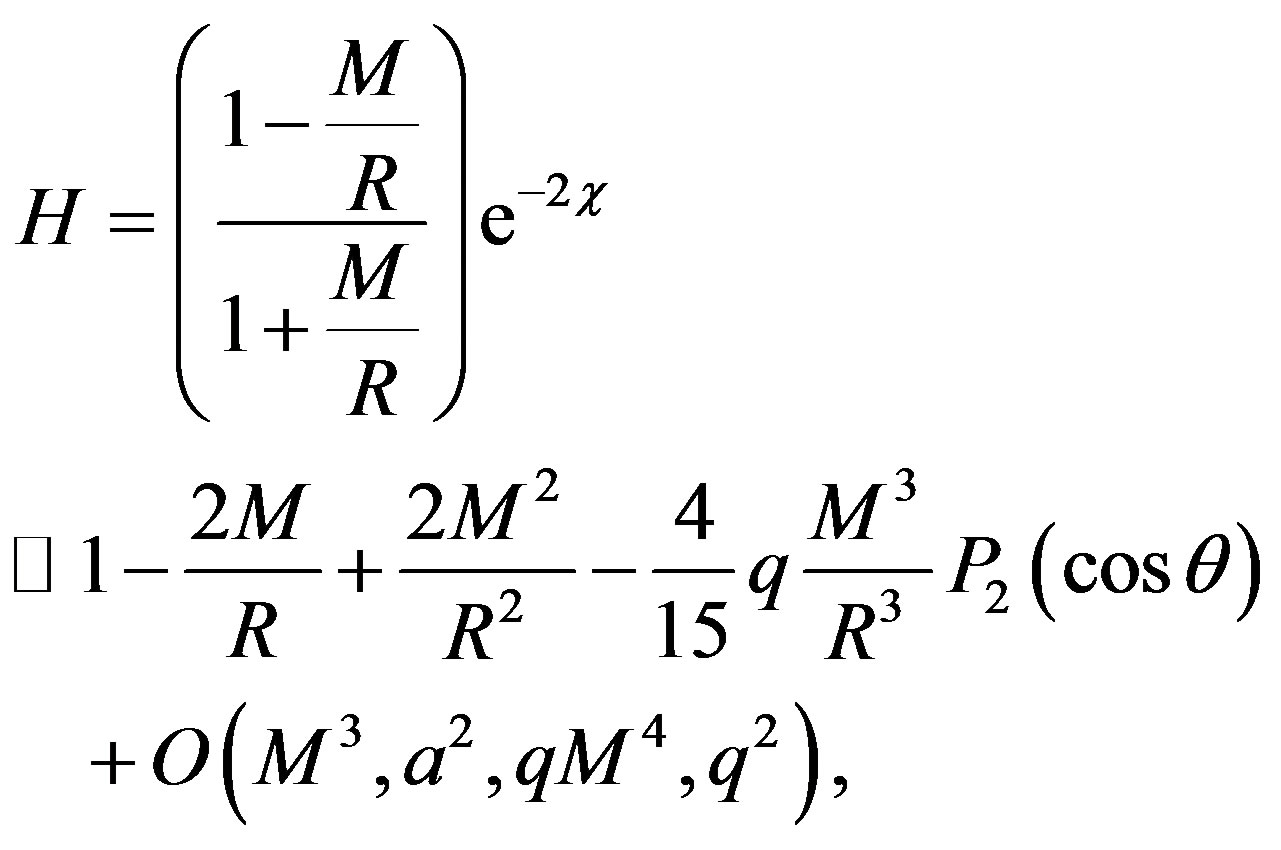
and
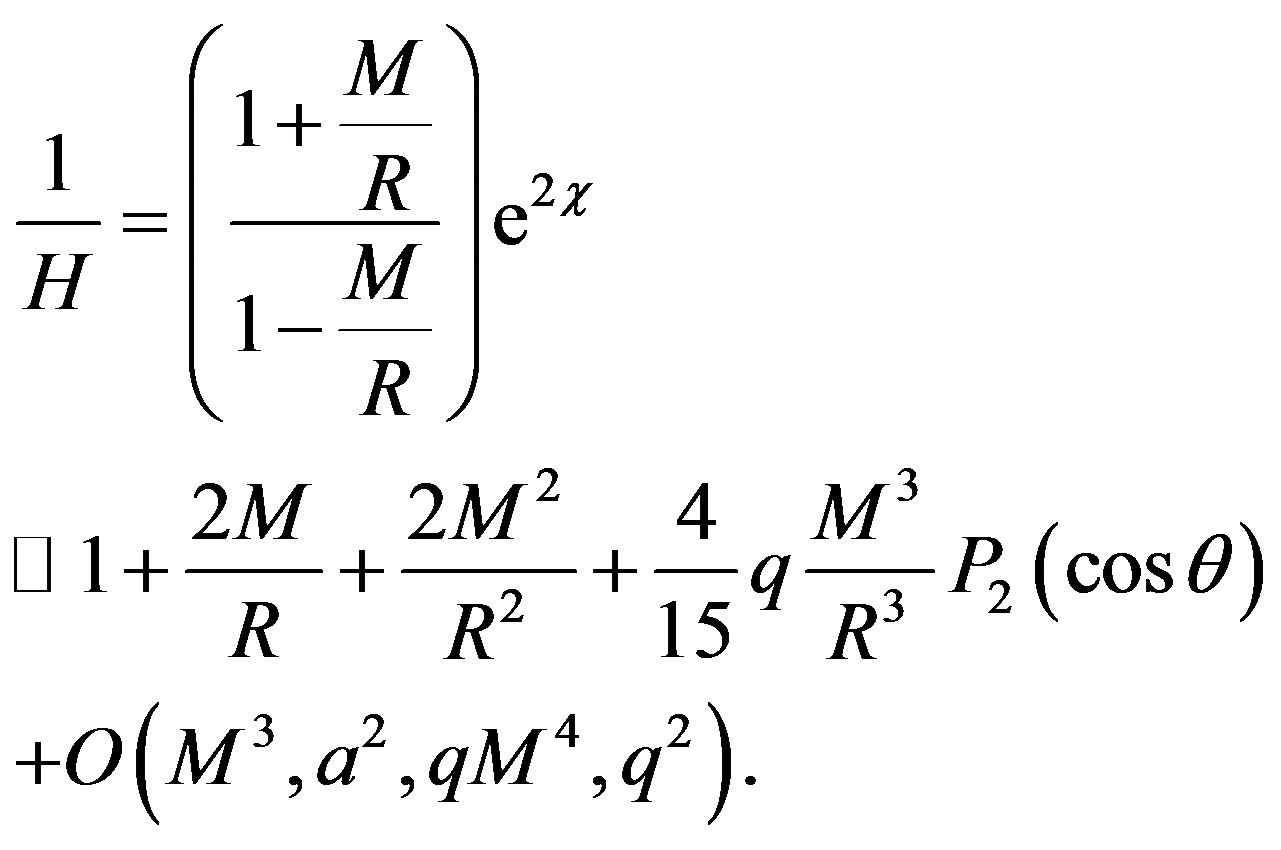
Noting that C = exp(-χ) is still given by (2) with r changed by R. Now, transforming the metric (13) into the Cartesian coordinates which are given by the usual relations

The resulting metric has the following form
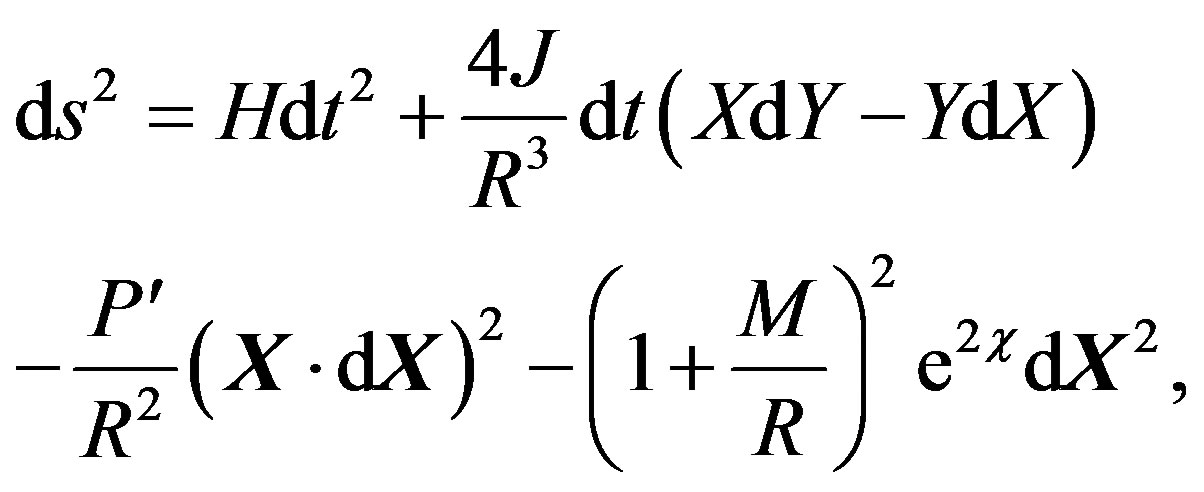
where X = (X, Y, Z)
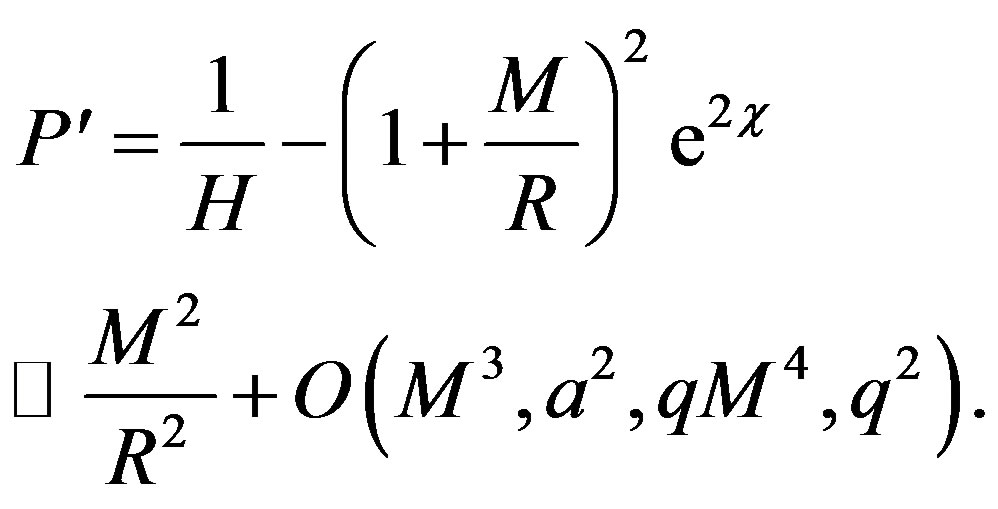
The former metric can be generalized as follows
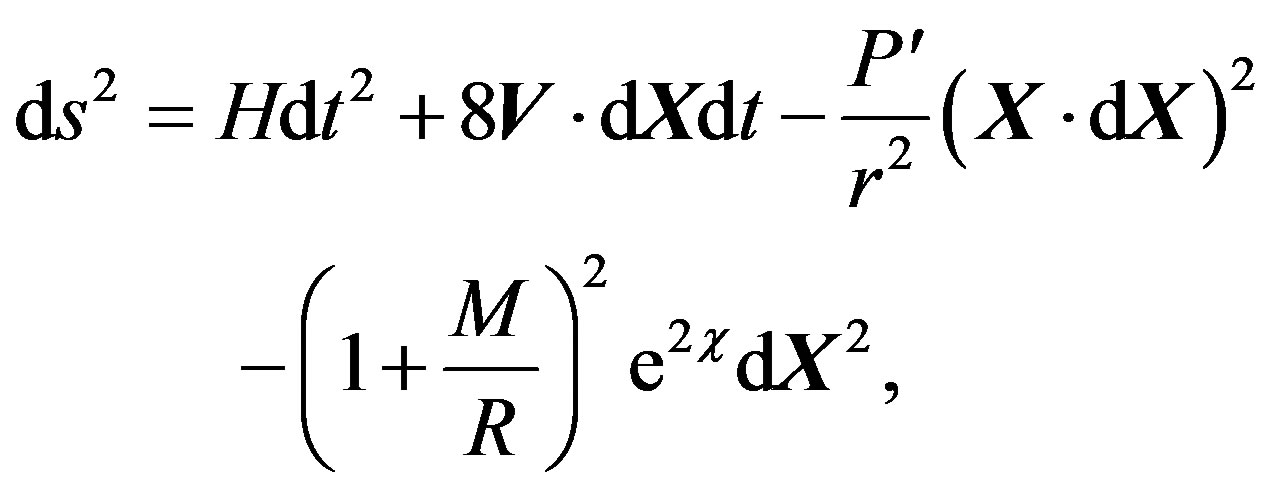 (14)
(14)
where
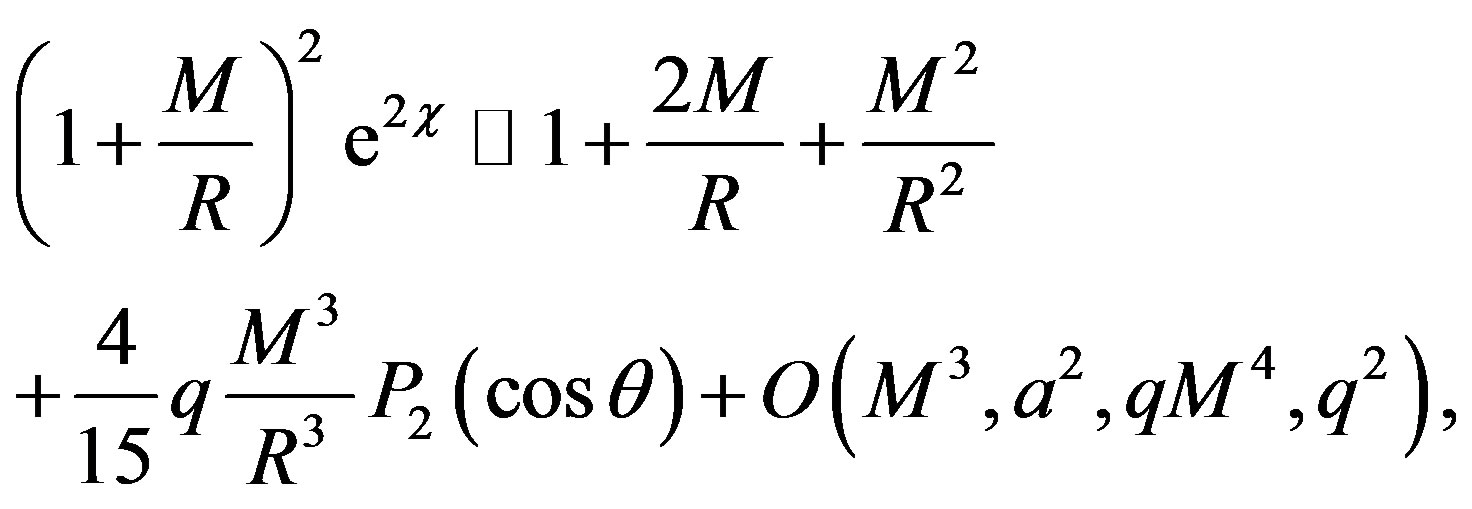
and the vector V is defined as
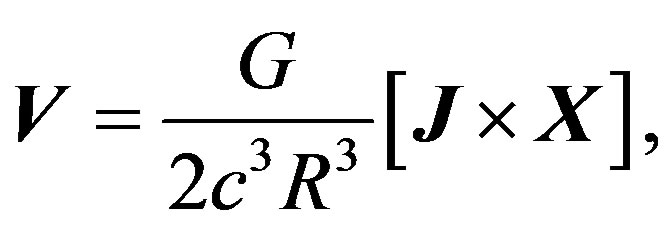
with J = Jej (ej is an unit vector in the direction of J).
7. Summary and Conclusion
In this paper, we include the rotational effect using the weak limit of the Erez-Rosen metric as seed metric into the Lewis-Papapetrou metric. Thus, a new metric with quadrupole moment and rotation in the weak limit is obtained. Generally speaking, the quadrupole moment is included in the metric, for instance, in gravitational lensing, through the expansion of the gravitational potential in a power series [22]. The resulting metric from our calculations includes the quadrupole moment in a natural form and is similar to the exterior metric obtained by Boshkayev et al. [11]. As we have seen in Section 4, our new metric agrees with the Hartle-Thorne solution [13], who obtained an interior metric that appropriately matches their exterior one, which guarantees the construction of an interior solution for our spacetime. This result indicates that our metric may be used to represent a compact astrophysical object. The new metric has many applications, for example, in calculations involving relativistic astrometry, in gravitational lens theory or planetary perihelion shift, and it is useful to have a metric that includes rotation and quadrupole moment. In relativistic astrometry, one needs a post-Newtonian metric to get some approximations from the deflection angle. It allows to get expressions for the right ascension α and declination δ for a celestial body [23,24] in the gravitational field including rotation and quadrupole moment. In gravitational lens theory, the deflection angle [25,26] can be used to obtain the lens equation, thereby the lensing properties for this new metric with intrinsic gravitational quadrupole may be studied. Another application of this metric is to calculate the planetary perihelion shift [27]. These applications will be the aim of forthcoming works.
Appendix
The Ricci tensor components are
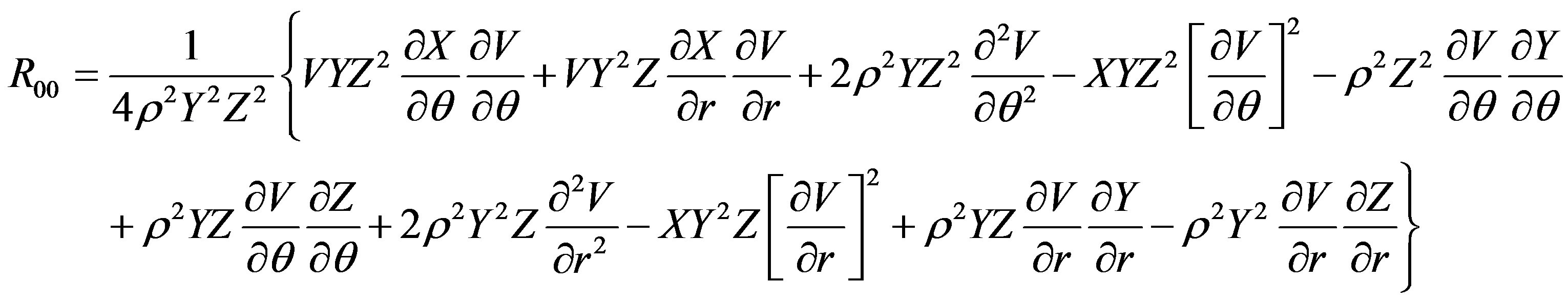
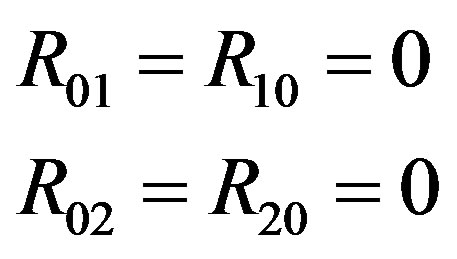

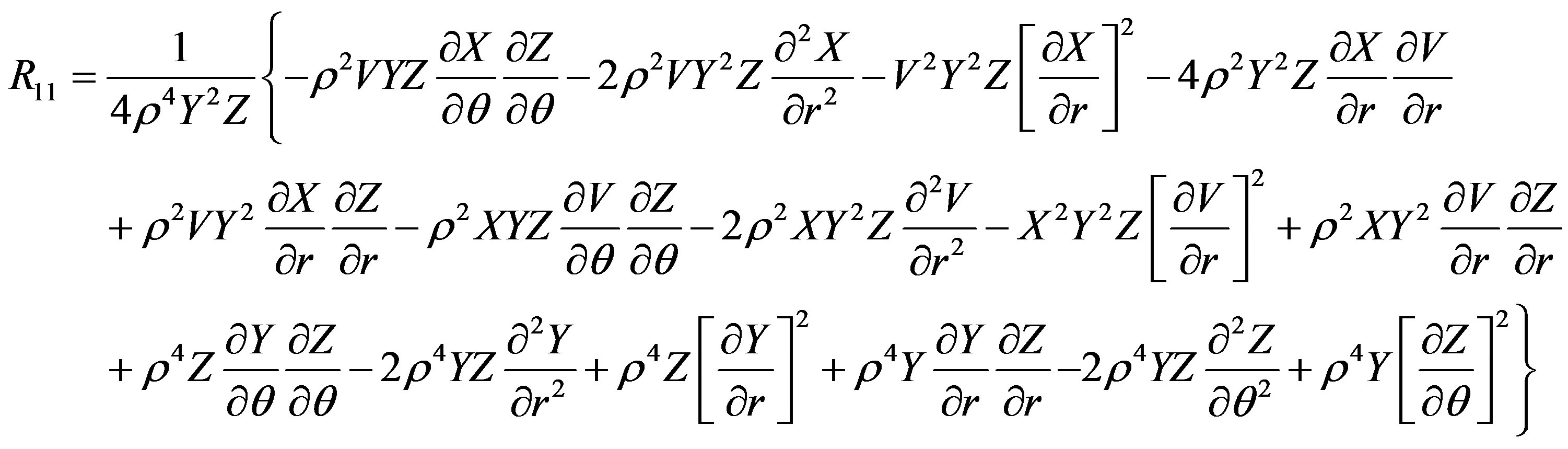
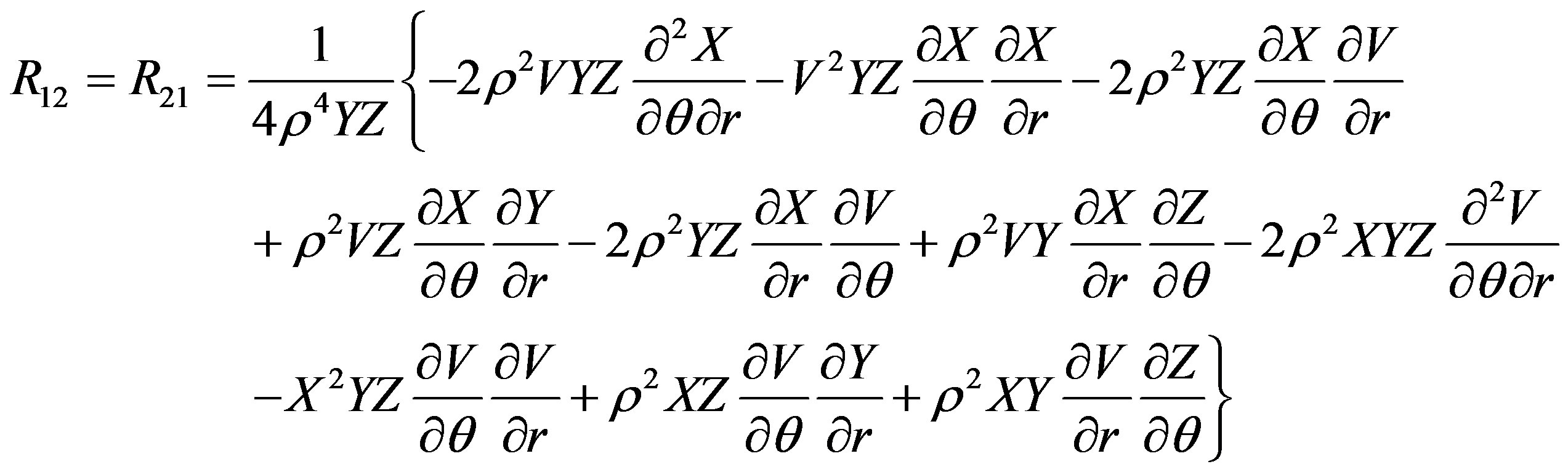
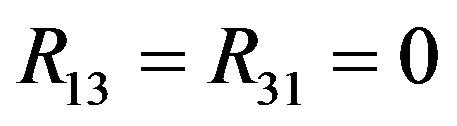
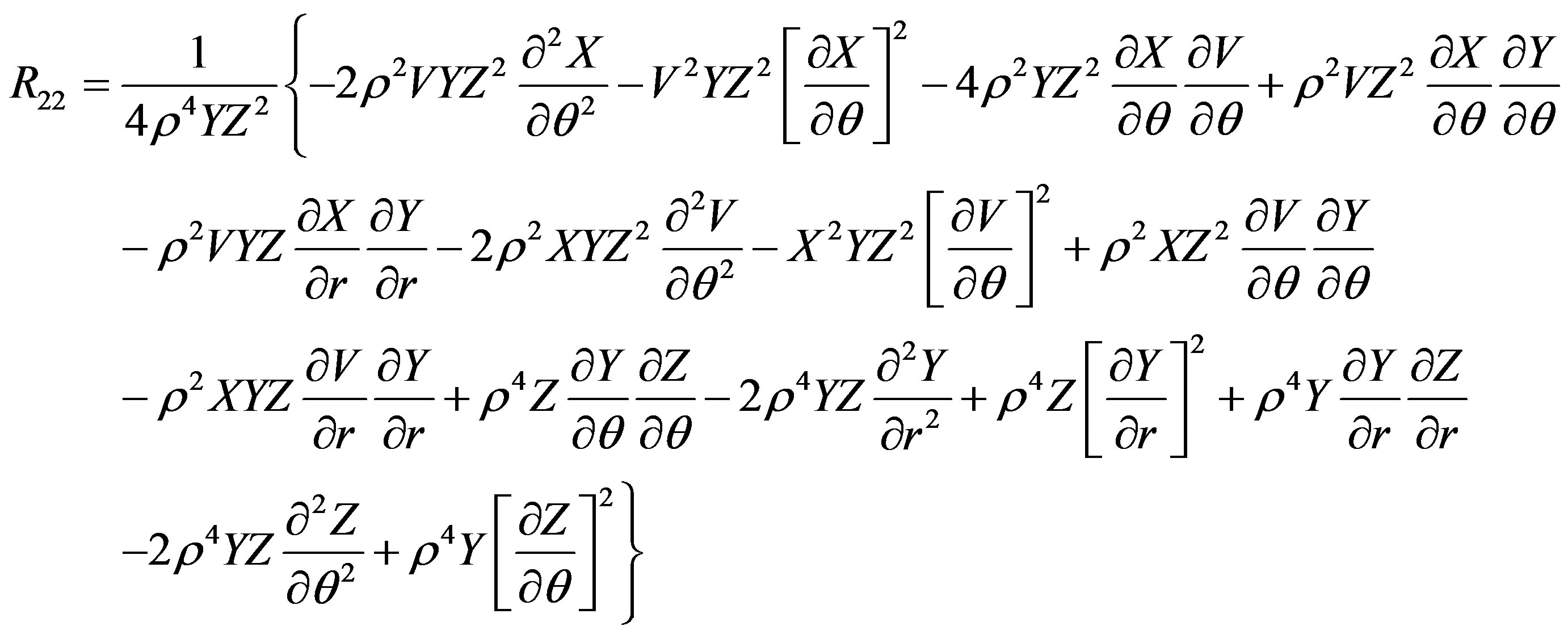

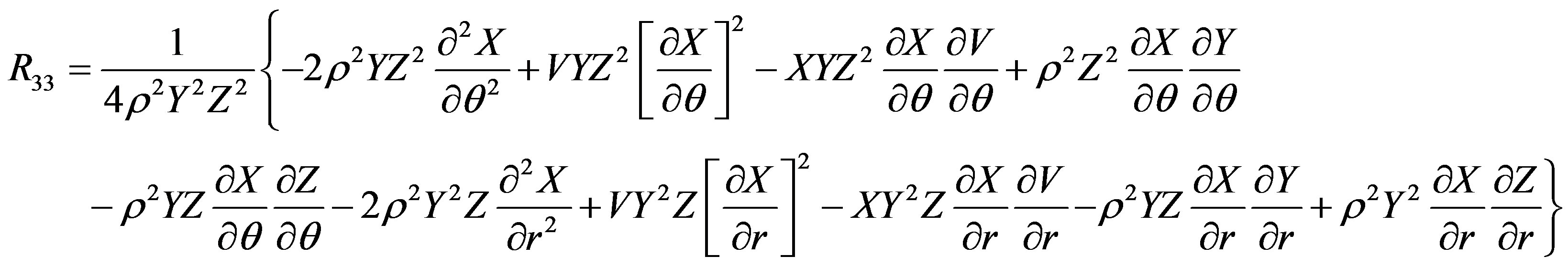
The scalar curvature is
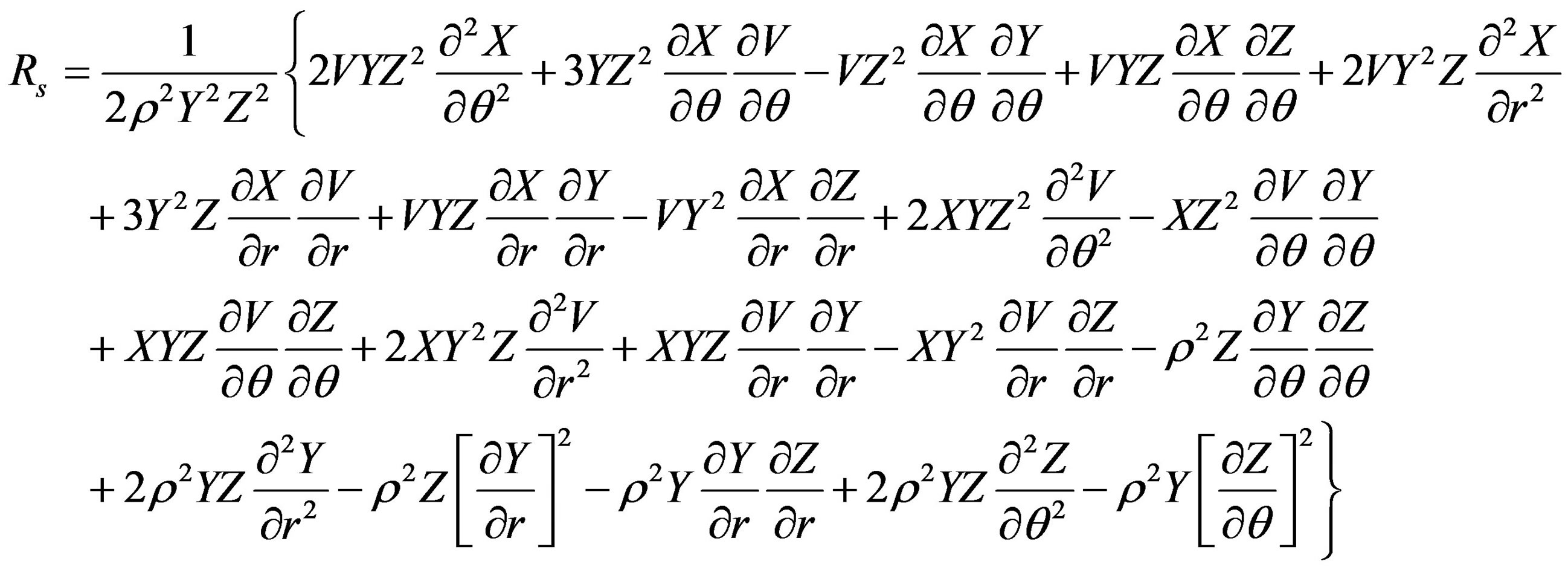
NOTES
#CICANUM (Nuclear Research Center), University of Costa Rica.