1. Introduction
Differentional geometry of point correspondences between projective, affine and euclid spaces of equal dimensions were studied and were studing by scientists till 1920. One can finds the analysis of obtained results to 1964 in the paper [1] by Ryzhkov.
Among all papers devoted to the theory of point correspondences between two three-dimensional spaces we must note papers [2] written by Svec, [3] written by Murracchini, [4] written by Mihailescu and [5] by Vranceanu. They introduce characteristic directions of point correspondences, consider some special classes of correspondences, show connections of point correspondences between spaces with different parts of differentional geometry.
Properties of point correspondences between n-dimensional projective, affine and euclid spaces are studied by Ryzhkov [6], Sokolova [7] and Pavljuchenko [8].
A straight line 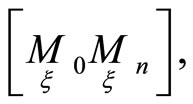 passing through the point
passing through the point is called a first order normal of a hypersurface of
is called a first order normal of a hypersurface of 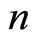 -dimensional projective space in the point
-dimensional projective space in the point 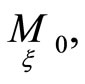 if the straight line has no other points with the tangent hyperplane of the hupersurface [9]. We call a
if the straight line has no other points with the tangent hyperplane of the hupersurface [9]. We call a 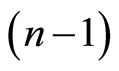 -dimensional plane as the second order normal of the hypersurface in the point
-dimensional plane as the second order normal of the hypersurface in the point  if the tangent hyperplane of the hypersurface in the point
if the tangent hyperplane of the hypersurface in the point 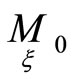 includes this
includes this  dimensional plane and this
dimensional plane and this  -dimensional plane does not pass through the point
-dimensional plane does not pass through the point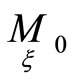 .
.
It is known that the main problem of nonmetric differentional geometry of a surface is a construction of invariant normalization of this surface. To construct an invariant first normal in a point of a surface it is necessary to use third-order differential neighbourhood of the point [10]. In our previous papers we showed that to construct an invariant first normal in points of two surfaces under point correspondences it is sufficient to use a second-order differential neighbourhood of corresponding points, but to construct an invariant second normal in points of two surfaces under point correspondences it is necessary to use third-order differential neighbourhood of the point.
In the current paper we will find invariant normalizations of the first and second orders of all hupersurfaces under the correspondence.
There exists a connection between the geometry of point correspondences between three spaces or surfaces and the theory of multidimensional 3-webs (Akivis [11]). We showed it in papers [12,13], devoted point correspondences between three projective spaces and between three hupersurfaces of projective spaces.
The theory of of multidimensional (n + 1)-webs is constructed in the paper [14] by Goldberg. In the current paper we will consider a connection between the geometry of point correspondences between 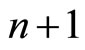 hypersurfaces of projective spaces and the theory of multidimensional (n + 1)-webs.
hypersurfaces of projective spaces and the theory of multidimensional (n + 1)-webs.
In the way of the investigation we use the exterior differentiation, tensor analysis and G.F.Laptev invariant methods [15].
2. Main Equations of Correspondence, the Sequence of Main Geometrical Objects
Let us consider n + 1 smooth hypersurfaces 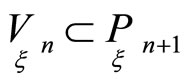
 of projective spaces and a point correspondence
of projective spaces and a point correspondence  between these hypersurfaces.
between these hypersurfaces.
Let 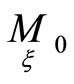 be corresponding points of hypersurfaces
be corresponding points of hypersurfaces . A correspondence
. A correspondence 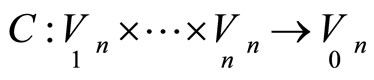 generates
generates 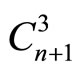 families point subcorrespondences
families point subcorrespondences obtained by fixation of n - 2 corres- ponding points and generates
obtained by fixation of n - 2 corres- ponding points and generates 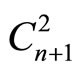 point mappings
point mappings  by fixation of n-1 corresponding points.
by fixation of n-1 corresponding points.
Mappings 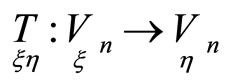 must be regular in neighbourhoods of points under correspondences of surfaces
must be regular in neighbourhoods of points under correspondences of surfaces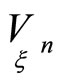 ,
,  and have the inverse mappings.
and have the inverse mappings.
We will assume, that surfaces  belong to different projective spaces
belong to different projective spaces . The geometry of correspondences under consideration will be studied according to the transformation group, which is a direct product of projective transformation groups of spaces
. The geometry of correspondences under consideration will be studied according to the transformation group, which is a direct product of projective transformation groups of spaces .
.
With any point  we associate a projective moving frame consisting of the point
we associate a projective moving frame consisting of the point  points
points 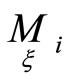
 of the tangent hyperplane of the hypersurface
of the tangent hyperplane of the hypersurface 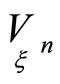 in the point
in the point  and a point
and a point  outside the tangent hyperplane.
outside the tangent hyperplane.
The equations of infinitesimal displacement of our projective frames 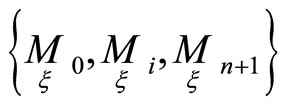 have the form:
have the form:
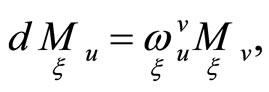 (1)
(1)
where 
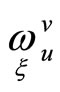 are 1-forms containing parameters, on which the family of frames in question depends, and their differentials. The forms
are 1-forms containing parameters, on which the family of frames in question depends, and their differentials. The forms 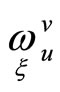 satisfy the structural equations of projective space:
satisfy the structural equations of projective space:
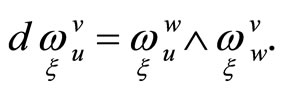
We can write equations of hypersurfaces 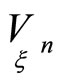 as follows:
as follows:
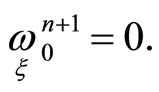 (2)
(2)
The Pfaffian forms  define displacements of corresponding points
define displacements of corresponding points 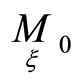 of hypersurfaces
of hypersurfaces . It follows that the forms
. It follows that the forms  satisfy the following linear relations:
satisfy the following linear relations:
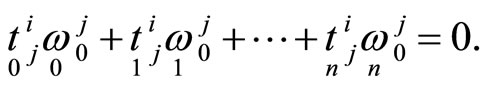 (3)
(3)
Since for  forms
forms 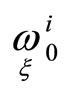 are linearly independent, therefore the following conditions are true:
are linearly independent, therefore the following conditions are true:

We can transform all frames of projective spaces in points 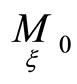 by setting
by setting . For new frames
. For new frames  we will have
we will have  By Equations (3) relations between forms
By Equations (3) relations between forms 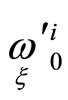 take the simplest case. Let us suppose that necessary transformations of frames are done and we can write relations between forms
take the simplest case. Let us suppose that necessary transformations of frames are done and we can write relations between forms  of frames
of frames 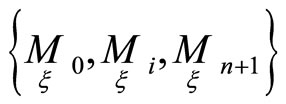 as follows
as follows
 (4)
(4)
Geometrically Equations (4) mean that frames in points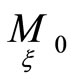 of spaces
of spaces  are chosen so that directions in points
are chosen so that directions in points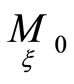 ,
, 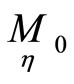 are corresponding by mappings
are corresponding by mappings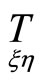 .
.
To find equations of a mapping  we fix points
we fix points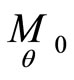 , where
, where . Using Equations (2), (4), we have
. Using Equations (2), (4), we have
 (5)
(5)
Consider projective mappings , where
, where

By Equations (1), (5) the following relations satisfy projective mappings:
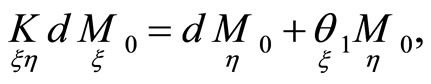
where —a quantity of the first order according to
—a quantity of the first order according to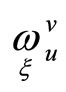 . The projective mapping
. The projective mapping  has a first order tangency with the mapping
has a first order tangency with the mapping  in corresponding points
in corresponding points 

Equations (2), (4) are main equations of our problem. With the help of exterior differentiation of these equations and applying Cartan’s lemma we obtain
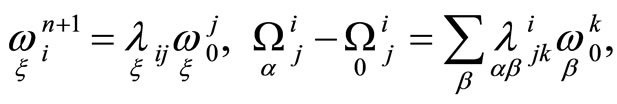 (6)
(6)
where 



Note that quadratic forms 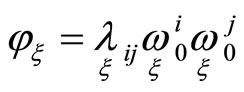 are asymptotic quadratic forms of hypersurfaces
are asymptotic quadratic forms of hypersurfaces 
Now in the family of frames we have equations of mapping  in the way
in the way
 (7)
(7)
and similar for 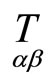
 (7’)
(7’)
where 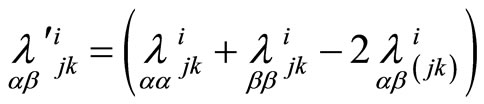 and
and .
.
To continue the system of Equations (6) we use exterior differentiation of these equations and Cartan’s lemma. We obtain new equations:
 (8)
(8)
To write these equations we used operators  and
and . Operator
. Operator  is defined by forms
is defined by forms 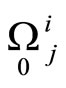 and we have
and we have
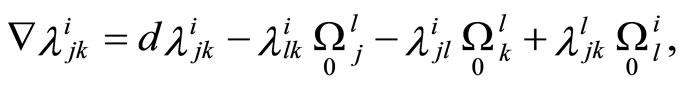
and similarly operators  are defined by forms
are defined by forms 
Quantities 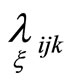 are symmetric with respect to the indices i, j and k, for quantities
are symmetric with respect to the indices i, j and k, for quantities 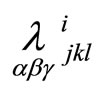 some additional finite conditions are true.
some additional finite conditions are true.
The system of quantities 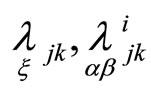 define the geometrical object according to G.F.Laptev invariant methods [15]. This object is the fundamental geometrical object of second order of point correspondence
define the geometrical object according to G.F.Laptev invariant methods [15]. This object is the fundamental geometrical object of second order of point correspondence
 .
.
If we continue Equations (8), we obtain the system of differentional equations of a sequence of fundamental geometrical objects of point correspondence under consideration

3. Characteristic Directions of Point Correspondences
Let us consider a mapping  If frames are fixed in corresponding points of hypersurfaces
If frames are fixed in corresponding points of hypersurfaces 
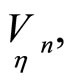 then the object
then the object  define the quadratic transformation of tangent directions of hypersurfaces
define the quadratic transformation of tangent directions of hypersurfaces

In geometry of point correspondences [1] directions are said to be characteristic if they are invariant according to these quadratic transformations. They must satisfy a system of equations
 (9)
(9)
A geodesic curve of hypersurface 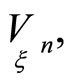 connected with the family of first order normals, is called a curve, whose 2-dimensional osculant plane passes through corresponding first order normals of hypersurface in every point (see for exsample [9]). If Pfaffian forms
connected with the family of first order normals, is called a curve, whose 2-dimensional osculant plane passes through corresponding first order normals of hypersurface in every point (see for exsample [9]). If Pfaffian forms 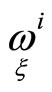 define a tangent direction to a curve
define a tangent direction to a curve 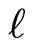 in a point
in a point 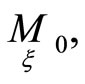 then relations
then relations

are the condition of the geometrical second order tangency of the curve  and a geodesic curve having the same tangent direction in this point
and a geodesic curve having the same tangent direction in this point .
.
Characteristic directions have the following property. If a curve 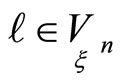 and a geodesic curve have second order tangency along a characteristic direction in the point
and a geodesic curve have second order tangency along a characteristic direction in the point 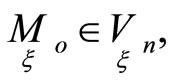 then the image
then the image  of the curve under
of the curve under 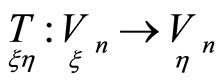 has the similar property in the point
has the similar property in the point 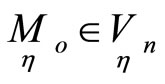 by the corresponding characteristic direction. It follows from Equations (7,) (7’), (9) and relations
by the corresponding characteristic direction. It follows from Equations (7,) (7’), (9) and relations

From geometric meaning of characteristic directions it is clear, that they depend on the choice of first order normals of a hypersurface and do not depend on the choice of second order normals.
We can rewrite Equations (9) in this way

We obtained equations of cubic cones. Characteristic directions are common generatrices of these cones.
Let us assume, that any direction  in a point
in a point 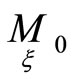 by some choice of a first order normal on hypersurfaces
by some choice of a first order normal on hypersurfaces  is characteristic for a mapping
is characteristic for a mapping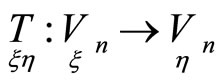 . Then the last equations must be sutisfied for any magnitudes
. Then the last equations must be sutisfied for any magnitudes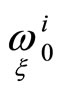 . Therefore, the following conditions are true for simillar correspondences
. Therefore, the following conditions are true for simillar correspondences

After calculations we get the relations:
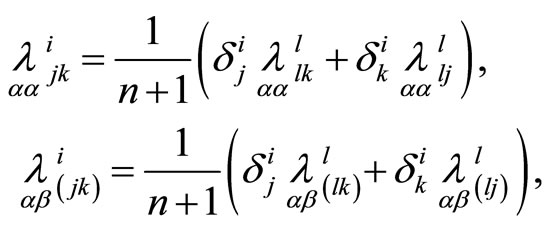 (10)
(10)
where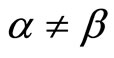 .
.
Theorem 1. If any direction  in a point
in a point  by any choice of first order normals on hypersurfaces
by any choice of first order normals on hypersurfaces 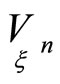 is characteristic for a mapping
is characteristic for a mapping , then for
, then for hypersurfaces
hypersurfaces  degenerate into hyperplanes and the correspondence becomes Godeux’s homography.
degenerate into hyperplanes and the correspondence becomes Godeux’s homography.
Really, let conditions of the theorem be true in corresponding points 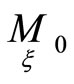 of all hypersurfaces
of all hypersurfaces  according to some first order normals
according to some first order normals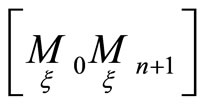 , then relations (10) are satisfied. We transform first order normals on hypersurfaces
, then relations (10) are satisfied. We transform first order normals on hypersurfaces 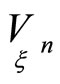 as follows
as follows where
where  are arbitrary quantities.
are arbitrary quantities.
We denote the values quantities  for new frames
for new frames 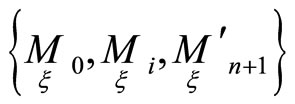 of hypersurfaces of the correspondence as
of hypersurfaces of the correspondence as 
Calculations show that

Since any direction  is characteristic according to first order normals on hypersurfaces
is characteristic according to first order normals on hypersurfaces 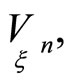 then quantities
then quantities 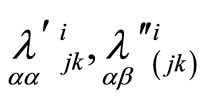 must also satisfy relations (10).
must also satisfy relations (10).
Let us consider the object  We have
We have

After substituting the values  and considering similar terms we obtain
and considering similar terms we obtain
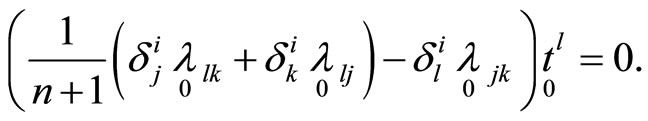
These relations must be true for any values  then
then
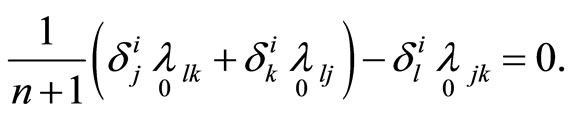
Contructing these relations with respect to the indices  and
and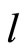 , we arrive at the equation
, we arrive at the equation  for
for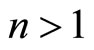 .
.
In a similar way we get .
.
It is known that hypersurfaces degenerate into hyperplanes if the asymptotic tensors 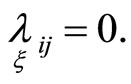
In this case a point correspondence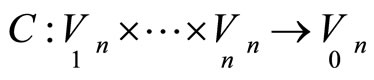 between hypersurfaces transforms into a point correspondence
between hypersurfaces transforms into a point correspondence 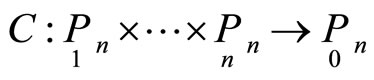 between hyperplanes. Since quantities
between hyperplanes. Since quantities 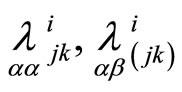 satisfy relations (10), then mappings
satisfy relations (10), then mappings 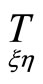 degenerate in projective mappings. Correspondences between projective spaces having similar properties are called Godeux’s homography.
degenerate in projective mappings. Correspondences between projective spaces having similar properties are called Godeux’s homography.
4. Invariant Normalizations of Hypersurfaces under Point Correspondences
Moving frames of hypersurfaces  under the correspondence depend on parameters of two types. There exsist principal parameters determined displacements of corresponding points
under the correspondence depend on parameters of two types. There exsist principal parameters determined displacements of corresponding points  of hypersurfaces
of hypersurfaces . Since points
. Since points 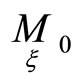 are connected by the correspondence the number of independent principal parameters is equal to
are connected by the correspondence the number of independent principal parameters is equal to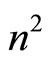 . By the Equations (4) 1-forms
. By the Equations (4) 1-forms  are independent linear combinations of differentials of principal parameters.
are independent linear combinations of differentials of principal parameters.
The Pfaffian forms  depend linearly on differentials of principal parameters and differentials of other parameters. The other parameters define trasformations of moving frames for fixing points
depend linearly on differentials of principal parameters and differentials of other parameters. The other parameters define trasformations of moving frames for fixing points . We denote values of forms
. We denote values of forms  as
as  for fixing principal parameters.
for fixing principal parameters.
We denote as 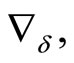
 values of operators
values of operators 
 and denote as
and denote as 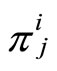 values of the Pfaffian forms
values of the Pfaffian forms  for fixing principal parameters.
for fixing principal parameters.
By Equation (6) we have:
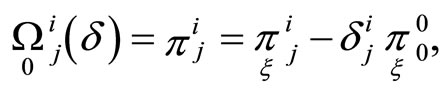
it follows 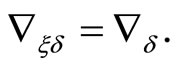
With the help of the operator  we can write Equation (8) for the case
we can write Equation (8) for the case 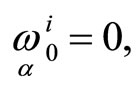 as follows:
as follows:
 (11)
(11)
where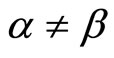 .
.
It follows from relations (11) that quantities  are relative tensors.
are relative tensors.
It is known that the main problem of nonmetric differentional geometry of a surface is a construction of invariant normalization of this surface. According to theory [10] for a hypersurface it is necessary to construct on the basis of the sequence of fundamental geometrical objects of the correspondence under consideration some quantities. These quantities must satisfy the following equations:
For the invariant first order normal (straight line)
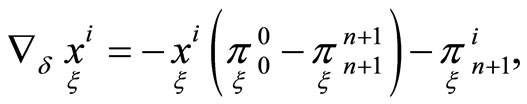 (12)
(12)
For the point on the invariant first order normal
 (13)
(13)
For the second order normal ( -dimensional plane inside the tangent hyperplane)
-dimensional plane inside the tangent hyperplane)
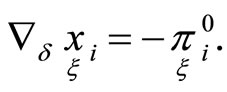 (14)
(14)
Below we will assume, that asymptotic quadratic forms of hypersurfaces  are nondegenerate. By virtue of this,
are nondegenerate. By virtue of this,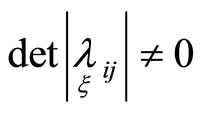 . It follows there exsist tensors
. It follows there exsist tensors  symmetric with respect to the indices
symmetric with respect to the indices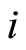 ,
,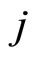 . These tensors sutisfy conditions
. These tensors sutisfy conditions  By Equation (11) we have differential equations:
By Equation (11) we have differential equations:

By Equation (11) we obtain:
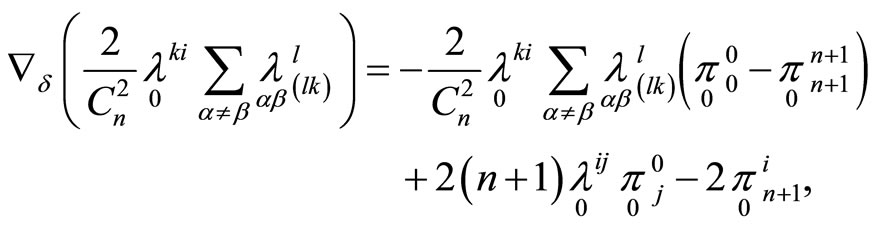
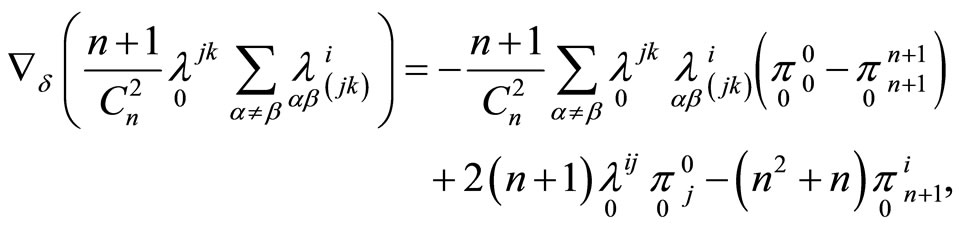
where . Note that for
. Note that for 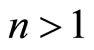 quantities
quantities
 (15)
(15)
satisfy equations

Therefore, by Equation (12) the quantities  define the invariant first order normal geometrical object of the hypersurface
define the invariant first order normal geometrical object of the hypersurface 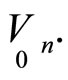 From Equation (11) we have
From Equation (11) we have

It follows that quantities
 (15’)
(15’)
satisfy Equation (12) and define the invariant first order normal geometrical objects of the hypersurfaces 
To construct the invariant second order normal geometrical object of the hypersurface 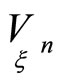 we consider quantities
we consider quantities
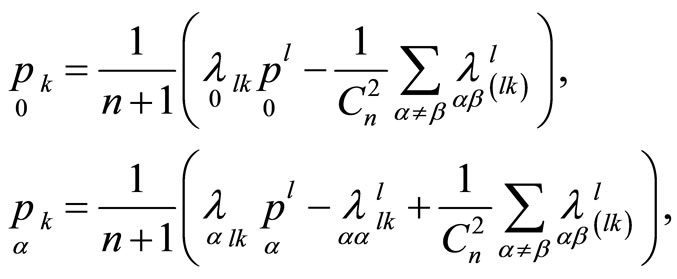 (16)
(16)
Calculations show that quantities 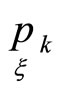 satisfy Equation (14).
satisfy Equation (14).
Thus, it is proved.
Theorem 2. If asymptotic quadratic forms of  hypersurfaces
hypersurfaces 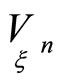 are nondegenerate and
are nondegenerate and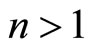 , then a point correspondence
, then a point correspondence 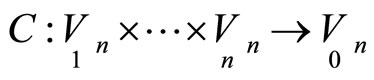 between these hypersurfaces determine invariant first and second orders normals for all hypersurfaces in a second-order differential neighbourhood of corresponding points.
between these hypersurfaces determine invariant first and second orders normals for all hypersurfaces in a second-order differential neighbourhood of corresponding points.
Note that to find necessary objects we used quantities . A quantity
. A quantity  may be used instead of the previous one. In general cases there exist
may be used instead of the previous one. In general cases there exist  different quantities
different quantities 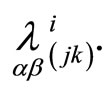 Therefore, different invariant normalizations of hypersurfaces exist. In the paper we used a symmetrical case.
Therefore, different invariant normalizations of hypersurfaces exist. In the paper we used a symmetrical case.
Below we will suppose that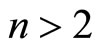 . The case
. The case  is considered in paper [12].
is considered in paper [12].
5. The Main Tensors of the Point Correspondence between n + 1 Hypersurfaces
Let us use the quantities  for construction of invariant frames of the correspondence. We introduce an invariant family of frames
for construction of invariant frames of the correspondence. We introduce an invariant family of frames 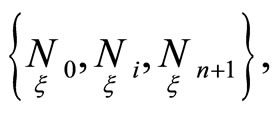 defined by points
defined by points

We denote Pfaffian forms of infinitesimal displacement of these frames as  Then relations between 1-forms
Then relations between 1-forms 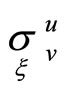 and
and  can be written as follows
can be written as follows
 (17)
(17)
By Equations (12), (14) quantities

 depend on differentials of principal parameters, therefore we can write forms
depend on differentials of principal parameters, therefore we can write forms  and
and  as follows
as follows
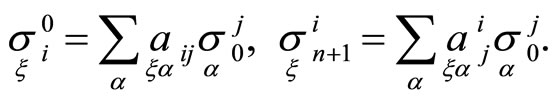 (18)
(18)
By new frames Equations (4), (6) of the corresponddence 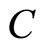 can be written in the form:
can be written in the form:
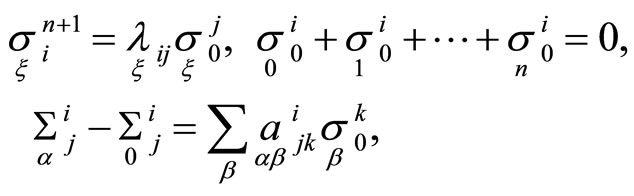 (19)
(19)
where 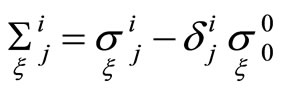 and
and
 (20)
(20)
Calculations show, that quantities 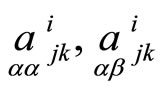 satisfy equations
satisfy equations
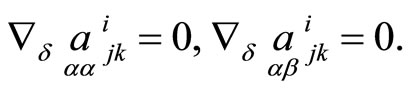
Therefore, quantities 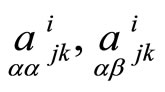 are absolute tensors of a second-order differential neighbourhood of the correspondence. They satisfy some additional conditions:
are absolute tensors of a second-order differential neighbourhood of the correspondence. They satisfy some additional conditions:

By relations (7), (7’), (19) in the family of new frames we have equations of mapping  in the way
in the way
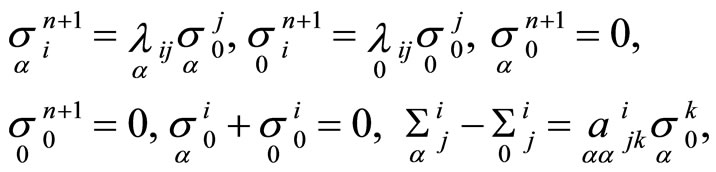
and similar for 

where 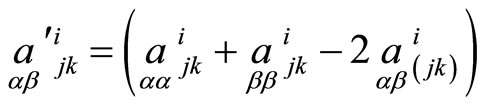 and
and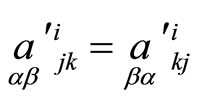 .
.
We will call tensors 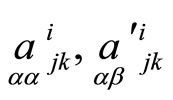 as main tensors of the correspondence. Tensors
as main tensors of the correspondence. Tensors 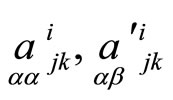 define quadratic transformations
define quadratic transformations 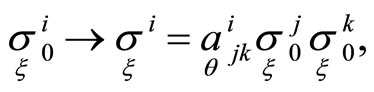 generated invariant charactiristic directions in corresponding points of hypersurfaces.
generated invariant charactiristic directions in corresponding points of hypersurfaces.
Let us consider correspondences  if there are relations
if there are relations

A point correspondence  is called geodesic, if any tangent directions of hypersurfaces
is called geodesic, if any tangent directions of hypersurfaces  in corresponding points
in corresponding points  became charactiristic for mappings
became charactiristic for mappings 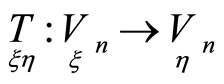 by some choice of the first order normals in these points.
by some choice of the first order normals in these points.
It is true.
Theorem 3. For 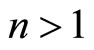 a point correspondence
a point correspondence 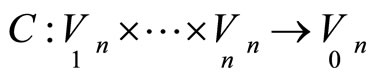 will be geodesic if ahd only if main tensors
will be geodesic if ahd only if main tensors 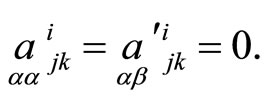
Really, let there exist  families of the first order normals of hypersurfaces under correspondence by them a point correspondence
families of the first order normals of hypersurfaces under correspondence by them a point correspondence  is geodesic. Then relations (10) must be true. In this case as follows from Equations (15), (15’) the first order normal objects of hypersurfaces
is geodesic. Then relations (10) must be true. In this case as follows from Equations (15), (15’) the first order normal objects of hypersurfaces 
By setting 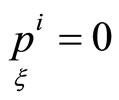 in relations (16), we get values of second order normal objects of hypersurfaces under correspondence in this way:
in relations (16), we get values of second order normal objects of hypersurfaces under correspondence in this way:

If we substitute values 
 in Equation (20) and use relations (10), then we obtain
in Equation (20) and use relations (10), then we obtain
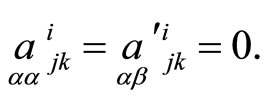
Conversely, if we use invariant first and second order normals in all hypersurfaces under correspondence and tensors
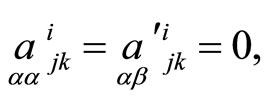 (21)
(21)
then relations (10) are true.
Any tangent direction  becomes charactiristic by invariant first order normals in corresponding points of hypersurfaces. It follows the point correspondence
becomes charactiristic by invariant first order normals in corresponding points of hypersurfaces. It follows the point correspondence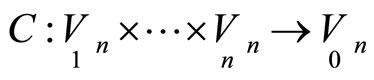 is geodesic.
is geodesic.
6. The Whole Projective-Invariant Normalization of Hypersurfaces under the Point Correspondence
To finish normalizations of hypersurfaces under consideration it is necessary to construct objects satisfying Equations (13). We prolong Equations (18). With the help of exterior differentiations and applying Cartan’s lemma we obtain new equations:
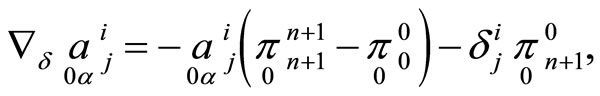

We construct quantities 
These quantities satisfy Equations (13) and define invariant points on the first order normals of hypersurfaces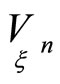 .
.
Let us find a geometrical meaning of chosen invariant points. We consider hypersurfaces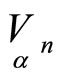 . We fix the hypersurface
. We fix the hypersurface , then
, then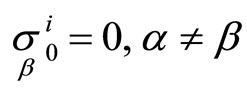 . The set of invariant first order normals of the hypersurface
. The set of invariant first order normals of the hypersurface 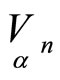 generates
generates 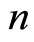 -parametrical fimily of straight lines. This set is called as a congruence of straight lines.
-parametrical fimily of straight lines. This set is called as a congruence of straight lines.
Let point 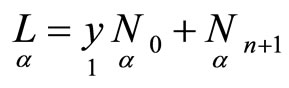 be a focus of the congruence of the straight lines
be a focus of the congruence of the straight lines  then infinitesimal displacement of focus
then infinitesimal displacement of focus 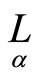 must belong to the straight line
must belong to the straight line 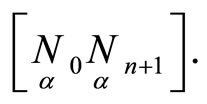 Since
Since

then focuses 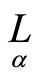 are obtained by conditions
are obtained by conditions
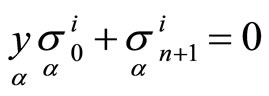
or
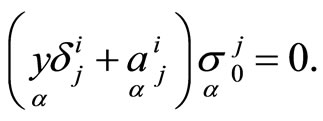
To get values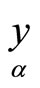 , defined focuses on the straight line
, defined focuses on the straight line  we consider the equation
we consider the equation

For roots of this equation we have

We can define the harmonic pole [16] on each straight line  of the congruence according to the point
of the congruence according to the point  and
and 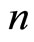 focuses by the relation
focuses by the relation

Let points 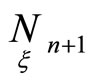 of frames coinside with invariant points
of frames coinside with invariant points 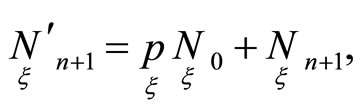 where quantities
where quantities  are defined by values
are defined by values  Other points of frames we leave without changing. After these transformations quantities
Other points of frames we leave without changing. After these transformations quantities 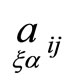 become absolute tensors and quantities
become absolute tensors and quantities 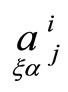 become relative tensors of the correspondence. Some relations are true
become relative tensors of the correspondence. Some relations are true
Forms  will depend only on differentials of principal parameters, that’s why they can be written as follows
will depend only on differentials of principal parameters, that’s why they can be written as follows 
It is proved.
Theorem 4. For 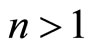 a point correspondence
a point correspondence define the whole projective-invariant normalization of hypersurfaces in the third differential neighbourhood of corresponding points.
define the whole projective-invariant normalization of hypersurfaces in the third differential neighbourhood of corresponding points.
7. Point Correspondences between (n + 1) Hypersurfaces of Projective Spaces and Multidimensional (n + 1)-Webs
A point correspondence 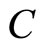 between
between  hyperspaces
hyperspaces  of projective spaces
of projective spaces  is a local differential
is a local differential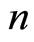 -quasigroup from the algebraic point of view. There exists an
-quasigroup from the algebraic point of view. There exists an  -web connected with this n-quasigroup. To find this web it is sufficient to consider a new manifold constructed as
-web connected with this n-quasigroup. To find this web it is sufficient to consider a new manifold constructed as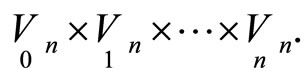 A correspondence C will be determined as an
A correspondence C will be determined as an 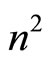 -dimesional smooth submanifold. There exist
-dimesional smooth submanifold. There exist 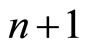 foliations of codimension
foliations of codimension 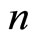 on this submanifold. Each foliation is determined by the hypersurface
on this submanifold. Each foliation is determined by the hypersurface . These foliations define
. These foliations define 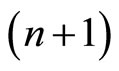 web W(n + 1, n) on the
web W(n + 1, n) on the 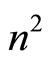 -dimensional submanifold.
-dimensional submanifold.
We introduce additional forms
 (22)
(22)
and quantities

where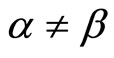 .
.
By relations (11) we have

Therefore, quantities  determine a tensor of a second-order differential neighbourhood of the correspondence. It can be written as
determine a tensor of a second-order differential neighbourhood of the correspondence. It can be written as

Using relations (17) we obtain

Thereforeforms  do not depend on a choice of frames in corresponding points of hypersurfaces.
do not depend on a choice of frames in corresponding points of hypersurfaces.
To write equations of  -web adjoined to correspondence
-web adjoined to correspondence  we use Equations (4), (22) and structural equations of projective spaces. We obtain
we use Equations (4), (22) and structural equations of projective spaces. We obtain
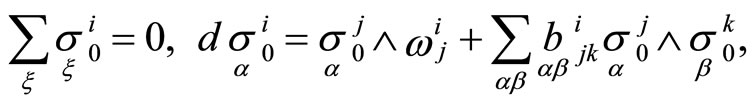

The equations show that forms  are the forms of an affine connection assosiated to the web
are the forms of an affine connection assosiated to the web  and tensors
and tensors 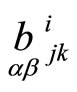 are the torsion tensor of
are the torsion tensor of  [14].
[14].
It is known that parallelizable webs [11] are the simplest class of (n + 1)-webs. A correspondence between (n + 1) hypesurfaces of projective spaces is said to be parallelizable if the (n + 1)-web of this correspondence is parallelizable. The necessary and sufficient conditions for correspondence to be parallelizable are relations
Calculations show that if hypersurfaces are given then parallelizable correspondences between (n + 1) hypesurfaces of projective spaces exist and depend on  functions in
functions in 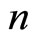 variables.
variables.
In paper [11] specific classes of webs are introduced called a class of (2n + 2)-adric webs. For these classes the following relations are true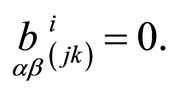
Comparing these relations with conditions (21), we note that they are true for geodesic correspondences, that’s why the (n + 1)-web adjoined to the geodesic correspondence between (n + 1) hypersurfaces of projective spaces is always (2n + 2)-adric web of type 2.
A point correspodence 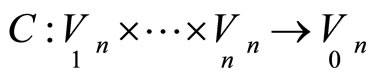 generates
generates  families point subcorrespondences
families point subcorrespondences
 obtained by fixation of n − 2 corresponding points. We can adjoin the web
obtained by fixation of n − 2 corresponding points. We can adjoin the web 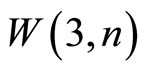 to each subcorrespondence
to each subcorrespondence 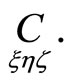 Let us find equations of correspondences
Let us find equations of correspondences  and equations of three-webs joined to them. Equations of correspondences
and equations of three-webs joined to them. Equations of correspondences  can be written in the following way
can be written in the following way
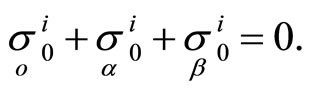
Substituting these values into equations of (n + 1)-web we have after transformations

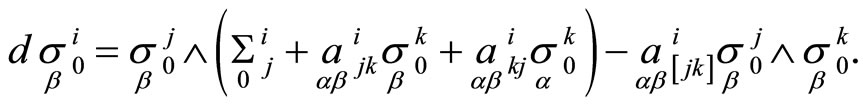
The forms

are connection forms of this three-web and the tensor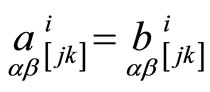 is the torsion tensor. If we take a correspondence
is the torsion tensor. If we take a correspondence 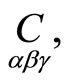 then the torsion tensor of three-web adjoined to
then the torsion tensor of three-web adjoined to 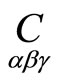 can be written as follows
can be written as follows
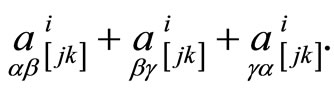
There exist the so-called paratactical three-webs [11]. In accordance with this, point correspondences between (n + 1) hypersurfaces of projective spaces are called paratactical, if all their subcorrespondences 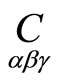 are paratactical ones (torsion tensors are equal zero). The following relations
are paratactical ones (torsion tensors are equal zero). The following relations

are conditions of the existence of paratactical correspondences.
8. Conclusions
We write main equations of a point correspondence between  hypersurfaces of projective spaces and construct the sequence of main geometrical objects of the correspondence. we define characteristic directions of a correspondence and prove that there exist invariant characteristic directions.
hypersurfaces of projective spaces and construct the sequence of main geometrical objects of the correspondence. we define characteristic directions of a correspondence and prove that there exist invariant characteristic directions.
We construct whole projective-invariant normalizations of all hupersurfaces and prove that invariant first and second orders normals for all hypersurfaces (n > 2) under point correspondences are determined in a secondorder differential neighbourhood of corresponding points. We single out main tensors of the correspondence and define some partial cases of correspondences.
We establish a connection between the geometry of point correspondences between 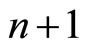 hypersurfaces of projective spaces and the theory of multidimensional (n + 1)-webs. In particular we prove that the (n + 1)-web adjoined to the geodesic correspondence between (n + 1) hypersurfaces of projective spaces is always (2n + 2)- adric web of type 2.
hypersurfaces of projective spaces and the theory of multidimensional (n + 1)-webs. In particular we prove that the (n + 1)-web adjoined to the geodesic correspondence between (n + 1) hypersurfaces of projective spaces is always (2n + 2)- adric web of type 2.