From Yang-Mills Photon in Curved Spacetime to Dark Energy Density ()
1. Introduction
While Einstein’s theory of relativity [1-8] predicts Emax = mc2 as the 100% energy density contained in the cosmos, sophisticated various measurements conducted over a long period of time such as COBE, WMAP and supernova measurements and analysis clearly indicate that nearly 95.5 of the 100% of this energy density cannot be accounted for except by indirect inference from the surprising unexpected increase in the speed of cosmic expansion observed [1,9-16]. The issue of the missing dark energy therefore has serious consequences for the very foundations of both cosmology and theoretical physics [7, 12]. Not surprisingly for those working on theories of unification and quantum gravity, the broad answer and resolution to all these contradictions is unification [16- 24]. In short this means that classical, relativistic and quantum mechanics must be fused together as explained and as graphically presented in Figure 1. In the present work, we use the basic concepts of a rather successful and the only approximate theory, namely Yang-Mills in curved spacetime [2,3] to revise Einstein’s energy equation [9,11]. The energy estimated using the new equation is surprisingly close to the results of actual cosmicmeasurements [1] and confirms the conclusion that Einstein’s equation E = mc2 is being wrongly interpreted outside of its range of validity and the assumptions underlie its derivation when applied to the entire cosmos. This is the case because Einstein’s famous equation is the sum of two components, namely the ordinary energy which we can measure and dark energy which we cannot measure directly [6-8,13]. We start herewith giving a very concise discussion of quantum filed theory in curved spacetime [2,3] and Yang-Mill’s theory [4-6]. Subsequently, we derive the new mass energy relation and reason that the 4.5% measured energy density is the energy of the quantum particle in 5D Kaluza-Klein spacetime [14] and that the 95.5% dark energy density is the energy of the quantum wave in the same D = 5 spacetime (see Figures 2 and 3). We also conclude that dark energy is the cause behind the anticlastic curvature producing negative gravity and thus the increased rate of cosmic expansion (see Figure 14 in Ref. [15] for a simple, informal experimental demonstration of how anticurvature ramifies at the holographic edge of the universe). One of our main conclusions is that quantum state and quantum wave are real as advocated particularly in [25] as well as [26-28].
2. Quantum Field Theory in Curved Spacetime (QFCS)
It is definitely an educated guess to presume that an accurate estimate of the magnitude of the entire energy in the cosmos needs a theory for quantum gravity [6]. Quantum field theory in curved spacetime on the other hand is very useful in situations where the quantum nature of a field and gravitation are both important but not in the case when only the quantum nature of gravity is crucial [6]. Thus quantum field theory in curved spacetime is just a reasonable approximation to a fully fledgedquantum gravity theory which could be applied to the entire universe [6,13,15]. In our present theory as in QFCS we treat gravity itself classically within the framework of Einstein’s general relativity. Thus we will have the same number of independent components of the Riemann tensor in 4D space, namely [7]
(1)
as well as the number of Killing vectors field which means [7]
(2)
Never the less and as we will see in what follows, the result obtained using QFCS [1,3] for the missing dark energy [1] is surprisingly very accurate when compared to other more exact theories and more importantly, when compared to the actual accurate cosmological measurements [1]. Now we turn our attention to the backbone of quantum field theory, namely Yang-Mills theory [4,5].
Figure 2. Graphic visualization of the transfinite set theoretical formulation of quantum physics [11-15].
3. Yang-Mills Theory and Its Three Photons
Guage invariance is fundamental to quantum field theory and Yang and Mills proposed in their famous theory to extend the set of possible gauge transformations [4,5]. Thus a potential field with 12 rather than 4 components was introduced. Consequently one finds that in YangMills theory we actually have not one photo but three, two of which are electrically charged [4,5]. The neutral photon is our ordinary photon and should not be confused with 
of the electroweak [7]. The critical point is that these are really massless photons. Massive photonlike rho-resonance can be changed without problem but there the situation is different. In any event we now have two more photons than in Einstein’s theory of relativity. In the next section we will see how Yang-Mills theory and Einstein’s classical relativity could be combined to use as a quantum Yang-Mills theory in curved spacetime [2-5] to produce an energy mass formula capable of dealing with the issue of the missing dark energy of the universe [1].
4. Yang-Mills Plus Einstein’s Gravity
It is now a trivial observation to realize that while Einstein’s special relativity formula depends upon a single
Figure 3. Quantum Measurement and dark energy of the quantum wave-A Case of the collapse of the HawkingHartle quantum wave of the cosmos [15].
Figure 4. Quantum relativity energy from a quantum filed theory in curved spacetime as the intersection of three fundamental theories (a) Einstein spacetime relativity with one photon
; (b) Yang-Mills theor with three photons, two charged and one neutral; (c) general theory of relativity with twenty degrees of freedom for the Riemannian tensor (graviton) in four dimensions. The result is the quantum gravity energy formula:
.
elementary messenger particle, the photon, a fusing of general relativity with Yang-Mills quantum electrodynamics will depend upon 23 degrees of freedom. These are the 20 independent components of the Riemann tensor in 4 dimensions or equivalently the 20 degrees of freedom of pure gravity in 8 dimensions [7]
(3)
and the additional 3 photons [4,5] so that the total is 20 + 3 = 23 in complete agreement with expectations [9].
On the other hand only the familiar neutral photon is assumed in the derivation of E = mc2 [7]. Consequently the additional degree of freedoms which did not enter into the derivation of E = mc2 are 23 - 1 = 22. This is not surprisingly equal to the number of dark dimensions of string theory when we subtract our familiar D(4) = 4 from the 26 dimensions of Bosonic string theory [7]. Invoking Weyl scaling and Nottale’s scale relativity principles [8] it is again an educated guess which can be substantiated via a watertight mathematical derivation that 
where 
should now be replaced by 
as follows
(4)
where the Lorentz factor also becomes 
[9-15]. This is a reduction in Emax by 95.4545% in astonishingly accurate agreement with the result of cosmological measurements [1-7,9-15]. The conceptual idea behind the present theory and analysis is demonstrated graphically in Figure 4. [1]. It is instructive to realize that the vital number, the 22 in the YangMills-Lorentzian factor could be deduced and interpreted in a variety of ways:
1. It is the inverse ratio of the second Betti number (b2) of the connected four dimensional spacetime of special relativity (b2 = 1) to that of a K3 Kähler used for superstring and M-theory compactification (b2 = 22), i.e. = 1/22. The conceptual idea behind the corresponding analysis is shown graphically in Figure 5 (see Ref. [9]).
2. It is the number of “dark” dimensions left from the 26 dimension of Bosonic strings after subtracting our familiar 3 + 1= 4 dimensions of classical relativity (26 – 4 = 22) as explained in [10]. Again the conceptual idea behind the three theories intersection concerned is elucidated in Figure 6.
3. It is the inverse of the square root of the dimensionality of 
exceptional Lie symmetry group of Heterotic string theory [7] after subtracting the 12 massless gauge bosons of the standard model, i.e. 
as explained in [9].
Figure 6. String theory view of quantum relativity energy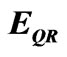 
from the intersection of three theories (a) special relativity D = 4 (b) Veneziano-Nambu Bosonic string D = 26 (c) Einstein’s relativity energy mass formula 
where c is the speed of light and m is the mass.
4. It is the inverse half the Hardy’s quantum entanglement 
where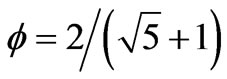 
when taking only the integer part of 
[7, 12]. In fact the measured ordinary energy could be calculated accurately as energy of a quantum particle 
while the dark energy is the energy of the quantum wave [14,15] given by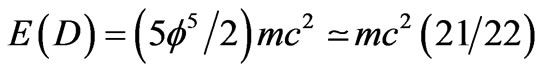 
as shown in Figure 4. For further details and explanation see Figures 2 and 3 and 7 as well as Ref. [8-15].
5. Conclusion and Prospects
Combining classical general relativity [7] with YangMills gauge theory [4,5], we produce an effective gravity-quantum field theory [2,3] which is a first order approximation to a possible quantum gravity theory [6]. Although the theory is only an approximation, the results for the missing dark energy obtained using this theory are more than excellent compared to those obtained using far more complex analyses such as superstring theory and the homology of Kähler manifolds (see Figure 1 and Figures 5-7). The most important point, however, is that our present theoretical result agrees completely with cosmic measurements from COBE to WMAP and type 1a supernova [1,15]. On the other hand, the result implies startling revelations about the real nature of dark energy being the energy of the quantum wave while ordinary energy is the energy of the quantum particle. Since measurement collapses the quantum wave, it follows that the dark energy could not be measured in the conventional way and requires quantum wave nondemolition sophisticated methods which are not yet sufficiently developed at the present time [26-28]. On the other hand, there are various other aspects which are relevant to the present discussion, particularly the equivalence between worm-
Figure 7. Flowchart for obtaining the dark energy of the quantum wave from Einstein’s relativity, Veneziano-NambuRegg Bosonic string theory and Kaluza-Klein theory.
holes and quantum non-locality, the thermodynamical informational aspect of gravity, negative Van der Waals forces simulating dark energy and the similarity between instantons [20-23] and the empty set as the physical meaning of topological pressure as far as negative gravity is concerned [11-15]. All these subjects and more will be dealt with in forthcoming publications.