1. Introduction
Convex programming deals with the minimization of a convex objective function over a convex set usually described by convex constraint functions. In the past various attempts have been made to weaken the convexity hypothesis [2-4] by replacing convex objective as well as constraint functions with more general ones and thus exploring the extent of optimality conditions applicability.
As a breakthrough to this, Lassere [1] showed that as far as KKT optimality conditions are concerned, the convexity (or any of its generalization) of the constraint functions can be replaced by the convexity of the feasible set described by the constraints. More precisely, Lassere considered the following convex optimization problem (CP):
(CP) minimize 
subject to


where  is a differentiable convex function and the feasible set
is a differentiable convex function and the feasible set

is a convex set while the :
:  are differentiable but not necessarily convex functions. To prove the necessity and sufficiency of KKT conditions in this framework Lassere considered the following non-degeneracy condition (ND1): For all
are differentiable but not necessarily convex functions. To prove the necessity and sufficiency of KKT conditions in this framework Lassere considered the following non-degeneracy condition (ND1): For all ,
,
 , whenever
, whenever  and
and  (ND1)
(ND1)
He showed that if the Slater constraint qualification1 and the above non-degeneracy condition (ND1) hold, then a feasible point x* of (CP) is a global minimizer if and only if it is a KKT point, that is,
 ,
,
and
 ,
, (KKT1)
(KKT1)
for some non-negative vector .
.
This work of Lassere [1] has been carried forward to the non-smooth case by Dutta and Lalitha [5]. They considered the same problem (CP) with the only difference being that the function f is a non-differentiable convex function and the convex set  is described by local Lipschitz constraint functions
is described by local Lipschitz constraint functions  which are not necessarily differentiable or convex. In terms of Dutta and Laltha [5] a point
which are not necessarily differentiable or convex. In terms of Dutta and Laltha [5] a point  is said to be a KKT point for the problem (CP) if there exist scalars
is said to be a KKT point for the problem (CP) if there exist scalars , such that
, such that

and

 (KKT2)
(KKT2)
where

denotes the sub-differential of f at x* and

denotes the Clarke sub-differential of the function  at x*.
at x*.
Further, Dutta and Lalitha [5] introduced the following non-smooth version (ND2) of Lassere’s non-degeneracy condition:
For all 
 (ND2)
(ND2)
In this modified setting Dutta and Lalitha [5] concluded that if each  is assumed to be regular in the sense of Clarke [6] and if the Slater constraint qualification and the non-degeneracy condition (ND2) hold, then a feasible point x* is a global minimizer of f over
is assumed to be regular in the sense of Clarke [6] and if the Slater constraint qualification and the non-degeneracy condition (ND2) hold, then a feasible point x* is a global minimizer of f over  if and only if it is a KKT point.
if and only if it is a KKT point.
The overall aim of this paper is to extend Lassere’s [1] results to a vector optimization problem over cones.
2. Preliminaries and Problem Formulation
We consider the following vector optimization problem (VOP) over cones:
(VOP) K – minimize 
subject to 
where  and
and  are differentiable functions, K and Q are closed convex cones with non-empty interiors in Rp and Rm respectively.
are differentiable functions, K and Q are closed convex cones with non-empty interiors in Rp and Rm respectively.
Let  be the set of feasible solutions of (VOP).
be the set of feasible solutions of (VOP).
The positive dual cone K* and the strict positive dual cone  of K are respectively defined as
of K are respectively defined as

and
 .
.
We begin by defining the notion of a KKT point in terms of (VOP).
Definition 2.1: A point  is said to be a KKT-point if there exist
is said to be a KKT-point if there exist  and
and  such that
such that
 and
and .
.
For the problem (VOP), the solutions are defined in the following sense:
Definition 2.2 [7]: A point  is called 1) a weak minimum of (VOP) if for all
is called 1) a weak minimum of (VOP) if for all 
 ;
;
2) a Pareto-minimum of (VOP) if for all 
 ;
;
3) a Strong minimum of (VOP) if for all 
 .
.
Let  denote the set of weak minimum solutions of (VOP).
denote the set of weak minimum solutions of (VOP).
The forthcoming optimality and duality results are based on suitable generalized convexity assumptions over cones, thus we recall some known definitions in the literature.
Definition 2.3 [8,9]: A function  is said to be
is said to be
1) K-convex at a point  if for every
if for every 
 .
.
2) K-pseudoconvex at  if for every
if for every 
 .
.
3) strongly K-pseudoconvex at  if for every
if for every 
 .
.
4) strictly K-pseudoconvex at  if for every
if for every 
 .
.
If f is K-convex (K-pseudoconvex, strongly K-pseudoconvex, strictly K-pseudoconvex) at every  then f is said to be K-convex (K-pseudoconvex, strongly K-pseudoconvex, strictly K-pseudoconvex) on Rn.
then f is said to be K-convex (K-pseudoconvex, strongly K-pseudoconvex, strictly K-pseudoconvex) on Rn.
On the lines of Jahn [10] we define Slater-type cone constraint qualification as follows:
Definition 2.4: The problem (VOP) is said to satisfy Slater-type cone constraint qualification at  if there exists
if there exists  such that
such that
 .
.
Note that if g is Q-convex at x* and the problem (VOP) satisfies Slater constraint qualification, that is, there exists  such that
such that , then (VOP) satisfies Slater-type cone constraint qualification at x*.
, then (VOP) satisfies Slater-type cone constraint qualification at x*.
Also, it is worth noticing that following the steps of Lassere [1] and Dutta and Lalitha [5] we can define the analogous non-degeneracy condition (ND3) for (VOP) as follows:
For all ,
,  , whenever
, whenever  and
and .
.
But if we assume that Slater-type cone constraint qualification holds at a point , then there exists
, then there exists  such that
such that

which means that for all  for which
for which
 , we have
, we have  which itself implies that
which itself implies that  and hence the nondegeneracy condition holds.
and hence the nondegeneracy condition holds.
Thus in the paper, we shall extend Lassere’s [1] results to the vector optimization problem (VOP) over cones but, unlike Lassere, to prove our results we need to assume only Slater-type cone constraint qualification at a point.
3. Optimality Conditions
In this section we prove several classical optimality results by taking generalized convexity assumptions over cones on the objective function and assuming the feasible set to be convex and with no convexity type restriction on the constraint function. It is clear that if the constraint function g in (VOP) is Q-convex then the feasible set F is convex, so we begin by exemplifying the fact that F can be convex without g being Q-convex.
Example 3.1: Consider  defined as
defined as

and
 .
.
Here g is not Q-convex, because if we take  and
and 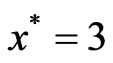 then
then
 .
.
But the feasible set  is convex. We have the following lemma.
is convex. We have the following lemma.
Lemma 3.1: If the feasible set F of (VOP) is convex then
 (1)
(1)
 .
.
Proof: Let F be convex and suppose
 satisfy
satisfy .
.
Assume that
 . (2)
. (2)
Now, for , we have
, we have

where
 .
.
This implies that.

Using (2) together with  for a sufficiently small,
for a sufficiently small,  , we get
, we get
 . (3)
. (3)
Since F is convex, therefore , that is,
, that is,
 so that
so that
 .
.
This contradicts (3). Hence the result.
The above lemma plays a pivotal role throughout the rest of the paper, thus we illustrate it by means of an example.
Example 3.2: Consider  and Q as defined in Example 3.1. Then we have already seen that g is not Q-convex whereas the feasible set F is convex.
and Q as defined in Example 3.1. Then we have already seen that g is not Q-convex whereas the feasible set F is convex.
Now, if we take , then
, then  if and only if
if and only if , and for this choice of m,
, and for this choice of m,

Also, for any other , there does not exist any
, there does not exist any  for which
for which .
.
Hence the lemma holds.
The following theorem serves the main purpose of the paper.
Theorem 3.1: Consider a feasible solution x* of the vector optimization problem (VOP) and assume that Slater-type cone constraint qualification holds at x*. If f is K-convex at x* and the feasible set F is convex then x* is a weak minimum of (VOP) if and only if it is a KKTpoint.
Proof: Let  be a weak minimum of (VOP). By Lemma 1 [11], there exist
be a weak minimum of (VOP). By Lemma 1 [11], there exist  and
and  not both zero such that
not both zero such that
 (4)
(4)
and
 . (5)
. (5)
If possible, let , then
, then  so that from (4), we get
so that from (4), we get
 . (6)
. (6)
Since Slater-type cone constraint qualification holds at x*, there exists 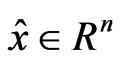 such that
such that
 which gives that
which gives that
 .
.
This together with (5) implies
 which contradicts (6). Therefore
which contradicts (6). Therefore .
.
Since the inequality (4) holds for every , we conclude that
, we conclude that
 (7)
(7)
and
 . (8)
. (8)
Hence x* is a KKT-point.
Conversely, let  be a KKT-point, that is, there exist
be a KKT-point, that is, there exist  and
and  such that (7) and (8) hold.
such that (7) and (8) hold.
Suppose x* is not a weak minimum of (VOP), so there exists  such that
such that
 . (9)
. (9)
Since f is K-convex at x*,
 . (10)
. (10)
By (9) and (10),
 which implies
which implies
 .
.
This, by (7), gives
 .
.
But this contradicts Lemma 3.1 as .
.
Hence  is a weak minimum for (VOP).
is a weak minimum for (VOP).
Theorem 3.2: Let f be K-pseudoconvex at  and suppose that F is convex. Further assume that Slater-type cone constraint qualification holds at x*. Then x* is a weak minimum of (VOP) if and only if it is a KKT-point.
and suppose that F is convex. Further assume that Slater-type cone constraint qualification holds at x*. Then x* is a weak minimum of (VOP) if and only if it is a KKT-point.
Proof: Proof follows on similar lines as Theorem 3.1.
Now we obtain sufficient optimality conditions for (VOP).
Theorem 3.3: Let f be K-convex at  and the feasible set F be convex and suppose that there exist
and the feasible set F be convex and suppose that there exist  and
and  such that (7) and (8) hold. Then
such that (7) and (8) hold. Then  is a Pareto minimum of (VOP).
is a Pareto minimum of (VOP).
Proof: Let if possible,  be not a Pareto minimum of (VOP). Then there exists
be not a Pareto minimum of (VOP). Then there exists  such that
such that
 . (11)
. (11)
Since f is K-convex at  we have
we have
 .
.
Using (11), we get
 .
.
Since  we have
we have
 .
.
Now proceeding as in the converse part of Theorem 3.1, we get a contradiction to Lemma 3.1. Hence  is a Pareto minimum of (VOP).
is a Pareto minimum of (VOP).
We now give an example to illustrate Theorem 3.3.
Example 3.3: Consider the problem
(VOP) K-Minimize 
Subject to 
where  and Q are as defined in Example 3.1 and
and Q are as defined in Example 3.1 and  and K are given by
and K are given by
 .
.
Then, as shown in Example 3.1, g is not Q-convex. while the feasible set  of (VOP) is convex. Also f is K-convex at
of (VOP) is convex. Also f is K-convex at .
.
It can be seen that for
 ,
,
 and
and .
.
Thus by Theorem 3.3,  is a Pareto minimum of (VOP).
is a Pareto minimum of (VOP).
Remark 3.1: Example 3.3 describes a vector optimization problem in which a Pareto minimum is obtained by applying Theorem 3.3 whereas it is impossible to do so using Lassere’s [1] results.
Theorem 3.4: Let f be strictly K-pseudoconvex at  and the feasible set F be convex and suppose that there exist
and the feasible set F be convex and suppose that there exist  and
and  such that (7) and (8) hold. Then
such that (7) and (8) hold. Then  is a Pareto minimum of (VOP).
is a Pareto minimum of (VOP).
Proof: Let if possible,  be not a Pareto minimum of (VOP).
be not a Pareto minimum of (VOP).
Then there exists  such that
such that
 .
.
Since f is strictly K-pseudoconvex at  we get
we get
 .
.
As , we have
, we have
 .
.
Now proceeding as in the converse part of Theorem 3.1, we get a contradiction to Lemma 3.1. Hence  is a Pareto minimum of (VOP).
is a Pareto minimum of (VOP).
Theorem 3.5: Let f be strongly K-pseudoconvex at  and the feasible set F be convex and suppose that there exist
and the feasible set F be convex and suppose that there exist  and
and  such that (7) and (8) hold. Then
such that (7) and (8) hold. Then  is a strong minimum of (VOP).
is a strong minimum of (VOP).
Proof: Let if possible,  be not a strong minimum of (VOP).
be not a strong minimum of (VOP).
Then there exists  such that
such that
 .
.
Since f is strongly K-pseudoconvex at  we get
we get
 .
.
As , we have
, we have
 .
.
Again proceeding as in the converse part of Theorem 3.1, we get a contradiction. Hence  is a strong minimum of (VOP).
is a strong minimum of (VOP).
4. Duality
With the primal problem (VOP), we associate the following Mond-Weir type dual program (MDP):
(MDP) K-maximize 
subject to
 (12)
(12)
 (13)
(13)
 .
.
Let FD denote the set of feasible solutions of (MDP).
Definition 4.1: A point  is said to be a weak maximum of (MDP) if
is said to be a weak maximum of (MDP) if
 .
.
Let  denote the set of weak maximum solutions of (MDP).
denote the set of weak maximum solutions of (MDP).
Theorem 4.1: (Weak Duality) Let  and
and . Assume that f is K-pseudoconvex at y and the feasible set F is convex, then
. Assume that f is K-pseudoconvex at y and the feasible set F is convex, then
 .
.
Proof: Let  and
and . Suppose to the contrary that
. Suppose to the contrary that
 (14)
(14)
Since f is K-pseudoconvex at y, (14) implies
 .
.
As , we get
, we get
 . (15)
. (15)
Since , therefore by Lemma 3.1,
, therefore by Lemma 3.1,
 . (16)
. (16)
Adding (15) and (16), we have
 which contradicts (12). Hence,
which contradicts (12). Hence, .
.
Theorem 4.2: (Strong Duality) Let  Assume that Slater-type cone constraint qualification holds at x*. If f is K-pseudoconvex at x* and the feasible set F is convex, then there exist
Assume that Slater-type cone constraint qualification holds at x*. If f is K-pseudoconvex at x* and the feasible set F is convex, then there exist  and
and  such that
such that  Further, if the conditions of Weak Duality Theorem 4.1 hold for all
Further, if the conditions of Weak Duality Theorem 4.1 hold for all  and
and , then
, then 
Proof: Since all the conditions of Theorem 3.2 hold, therefore there exist  and
and  such that
such that

and
 .
.
Thus  Further if
Further if , then there exists
, then there exists  such that
such that

which contradicts Theorem 4.1.
Hence, 
Theorem 4.3: (Converse Duality) Let

Assume that f is K-pseudoconvex at  and the feasible set F is convex. Then
and the feasible set F is convex. Then 
Proof: Suppose  Then there exists
Then there exists  such that
such that
 .
.
Since f is K-pseudoconvex at  we get
we get
 so that,
so that,
 (17)
(17)
Also,  , so that by Lemma 3.1,
, so that by Lemma 3.1,
 . (18)
. (18)
Adding (17) and (18), we have
 which contradicts (12). Hence,
which contradicts (12). Hence, 
5. Conclusion
This paper gives a new direction to the search for solution of a vector optimization problem over cones. We have shown that, with Slater-type cone constraint quailfication, convexity of the feasible set can replace the cone-convexity (or any of its generalization) of the constraint functions, and then we just need to assume the cone-convexity (or a suitable generalization) of the objective function to prove the necessity and sufficiency of the KKT optimality conditions. Moreover, a Mond-Weir type dual has been formulated in the modified situation and various duality results have been established.
6. Acknowledgements
The first author is grateful to the University Grants Commission (UGC), India for offering financial support.
NOTES