Comparison of the Linear Sigma Model and Chiral Perturbation Theory for Nucleon Properties ()
1. Introduction
A lot of groups have made significant progress towards understanding the fundamental baryon properties using several models [1-5]. One of the effective models in describing hadron properties is the Linear Sigma Model (LSM) [2,4], which serves as a good low-energy effective theory in order for one gain some insight into Quantum Chromodynamics (QCD). The LSM [6] provides an illuminating example of spontaneous chiral symmetry breaking in strong interactions, and has been studied extensively in the literature [7]. Some of the consequences of this model, however, are known to be in conflict with observation. In [6,8], it is argued that spontaneous symmetry breaking of the QCD Lagrangian gives rise to an effective chiral Lagrangian of Gell-Mann-Levy sigma model from involving explicit quark, scalar-isoscalar meson (sigma, σ), and pseudoscalar-isovector meson (pion, π) degree of freedom. There is no confinement in this model, and nucleons appear as bound states of a three-quark system. The bound states of the model have been solved in mean field approximation using the hedgehog ansatz [4] which assumes a configuration space-isospin correlation for the pion field,  , and for the quarks. One drawback of this ansatz is that it breaks both rotational
, and for the quarks. One drawback of this ansatz is that it breaks both rotational 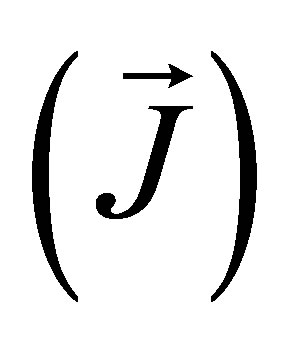 and isospin invariance
and isospin invariance  (although the grand spin
(although the grand spin  remains conserved) requiring some projection onto physical states at the end. On the other hand, Chiral Perturbation Theory (χPT) [9-11] is a low momentum effective field theory for QCD written as an expansion in small momenta and quark masses, and it has become an invaluable tool for subatomic physics. With only the lightest octets of pseu- doscalar mesons and spin-1/2 baryons, χPT is order-byorder renormalizable and physical results are independent of whichever regularization prescription that is chosen. The addition of lightest decuplet of spin-3/2 baryons introduces a new physical scale, and the mass difference between decuplet and octet baryons, which does not vanish in the chiral limit (i.e. when quark masses vanish). However, this mass difference is similar in size to the pseudoscalar meson masses, so the strict chiral expansion can be generalized to a small scale expansion where the power counting is now meaningful even if the decuplet baryons are presented [11,12]. The perturbative technique allows a quantized treatment of the pion field up to a given order in accuracy. Although formulated on the quark level, where confinement is put in phenomenologically, chiral perturbative quark models are formally close to χPT on the hadron level. As a further development of chiral quark models with a perturbative treatment of the pion cloud [12-17], the Tuebingen group extended the relativistic quark model for the study of the low-energy properties of the nucleon [18,19]. In Section 2, LSM is presented. (χPT) is given in Section 3 and our results and conclusion are in Section 4.
remains conserved) requiring some projection onto physical states at the end. On the other hand, Chiral Perturbation Theory (χPT) [9-11] is a low momentum effective field theory for QCD written as an expansion in small momenta and quark masses, and it has become an invaluable tool for subatomic physics. With only the lightest octets of pseu- doscalar mesons and spin-1/2 baryons, χPT is order-byorder renormalizable and physical results are independent of whichever regularization prescription that is chosen. The addition of lightest decuplet of spin-3/2 baryons introduces a new physical scale, and the mass difference between decuplet and octet baryons, which does not vanish in the chiral limit (i.e. when quark masses vanish). However, this mass difference is similar in size to the pseudoscalar meson masses, so the strict chiral expansion can be generalized to a small scale expansion where the power counting is now meaningful even if the decuplet baryons are presented [11,12]. The perturbative technique allows a quantized treatment of the pion field up to a given order in accuracy. Although formulated on the quark level, where confinement is put in phenomenologically, chiral perturbative quark models are formally close to χPT on the hadron level. As a further development of chiral quark models with a perturbative treatment of the pion cloud [12-17], the Tuebingen group extended the relativistic quark model for the study of the low-energy properties of the nucleon [18,19]. In Section 2, LSM is presented. (χPT) is given in Section 3 and our results and conclusion are in Section 4.
2. The Linear Sigma Model
We describe the interactions of quarks with σ-mesons and pions by Birse and Banerjee [5]. The Lagrangian density is,
 (1)
(1)
where
 (2)
(2)
is the meson-meson interaction potential and the  and π are the quark, (scalar, isoscalar) sigma and (pseudoscalar, isovector) pion fields, respectively. In the semiclassical or mean-field approximation the meson fields are treated as time-independent classical fields. This means that we are replacing power and products of the meson fields by corresponding powers and products of their expectation values.
and π are the quark, (scalar, isoscalar) sigma and (pseudoscalar, isovector) pion fields, respectively. In the semiclassical or mean-field approximation the meson fields are treated as time-independent classical fields. This means that we are replacing power and products of the meson fields by corresponding powers and products of their expectation values.
The meson-meson interactions in Equation (2) lead to hidden chiral  symmetry with
symmetry with  taking on a vacuum expectation value
taking on a vacuum expectation value
 (3)
(3)
where  Mev is the pion decay constant. The last term in Equation (2) is included to break the chiral symmetry. It leads to partial conservation of axial-vector isospin current (PCAC). The parameters
Mev is the pion decay constant. The last term in Equation (2) is included to break the chiral symmetry. It leads to partial conservation of axial-vector isospin current (PCAC). The parameters  can be expressed in terms of
can be expressed in terms of , the mass of the σ and mass of the π meson:
, the mass of the σ and mass of the π meson:
 (4)
(4)
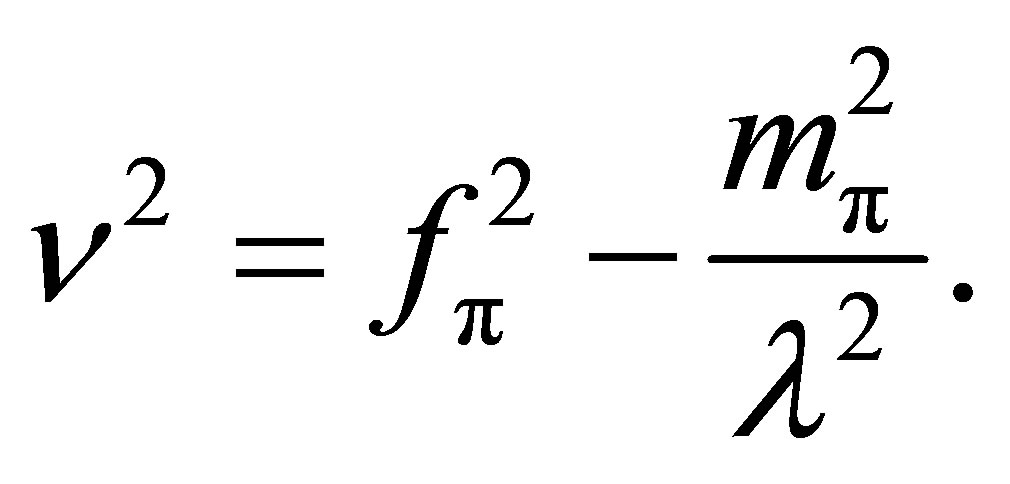 (5)
(5)
Now we expand around the extremum, with the shifted field defined as
 (6)
(6)
Substituting Equation (6) into Equation (1) we get :
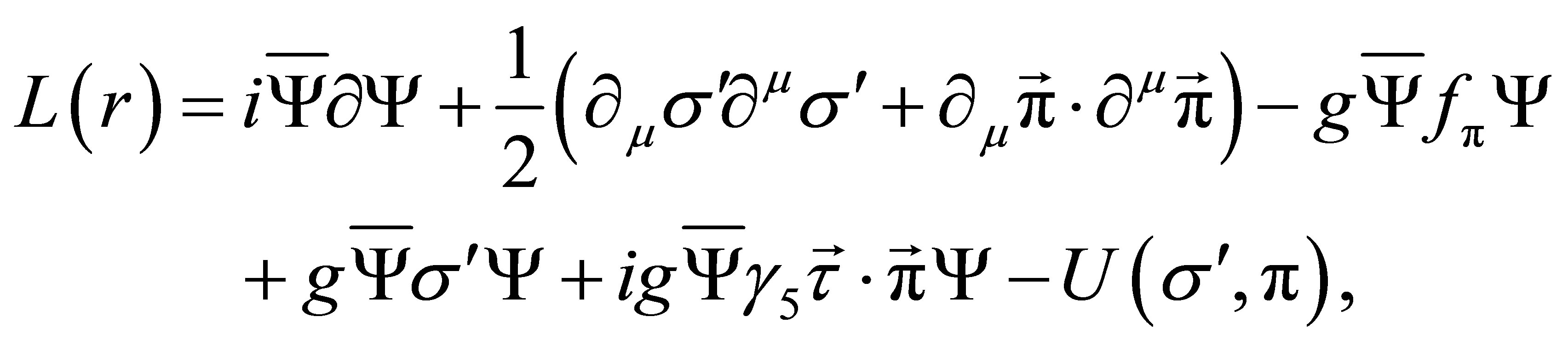 (7)
(7)
with
 (8)
(8)
The time-independent fields  and
and  are to satisfy the Euler-Lagrangian equations, and the quark wave function satisfies the Dirac eigenvalue equation. Substituting Equation (7) into the Euler-Lagrangian equation we get:
are to satisfy the Euler-Lagrangian equations, and the quark wave function satisfies the Dirac eigenvalue equation. Substituting Equation (7) into the Euler-Lagrangian equation we get:
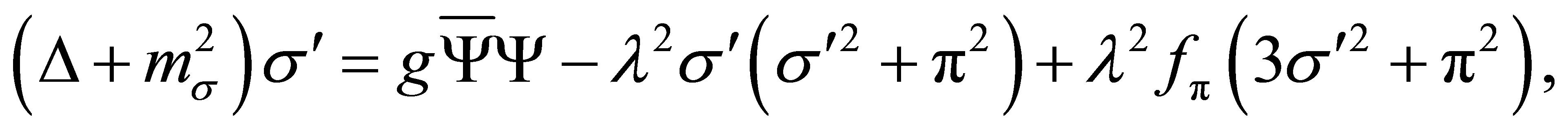 (9)
(9)
 (10)
(10)
where  refers to Pauli (iso)spin-matrices,
refers to Pauli (iso)spin-matrices,
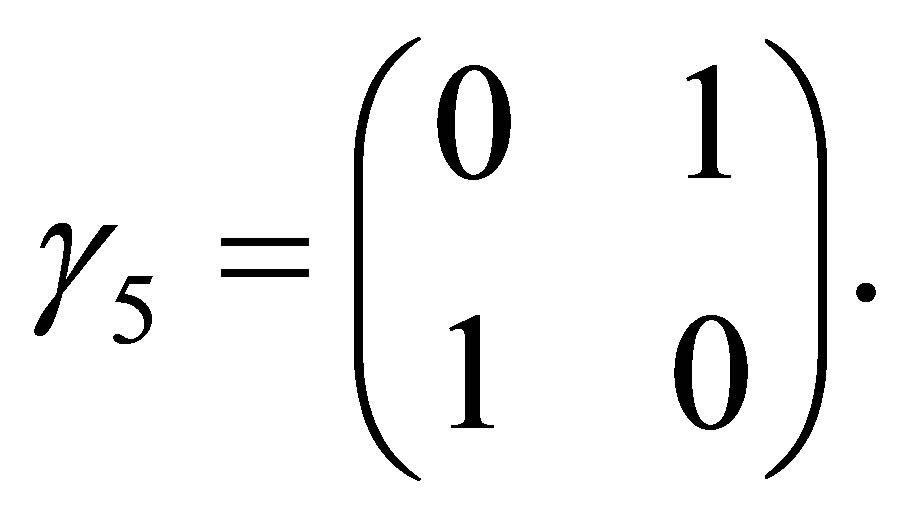
By using Hedgehog Ansatz [4] where
 (11)
(11)
The Dirac wave function  and
and  are given by
are given by
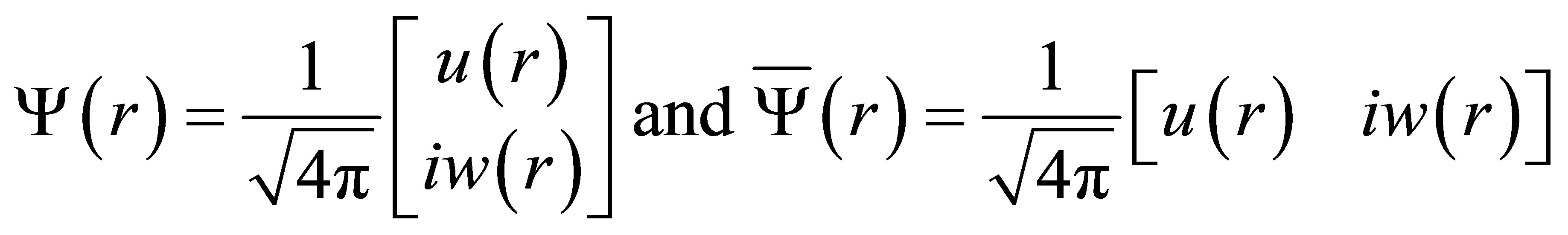 (12)
(12)
where  and
and 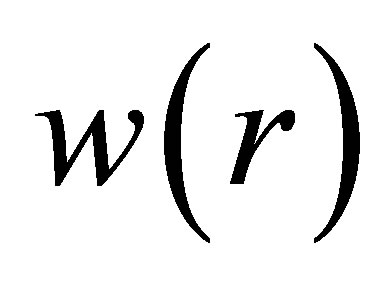 are the upper and lower component of the Dirac wave function. The chiral Dirac equation for the quarks are
are the upper and lower component of the Dirac wave function. The chiral Dirac equation for the quarks are
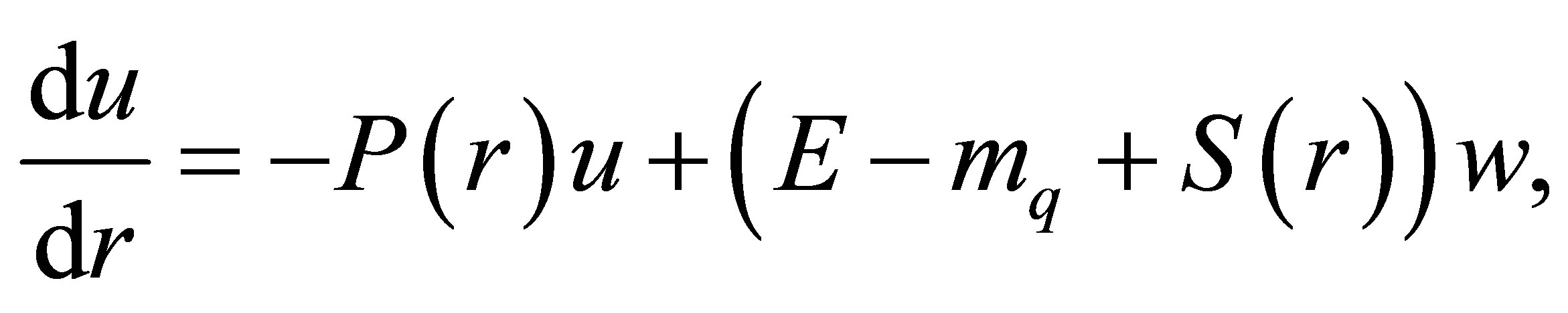 (13)
(13)
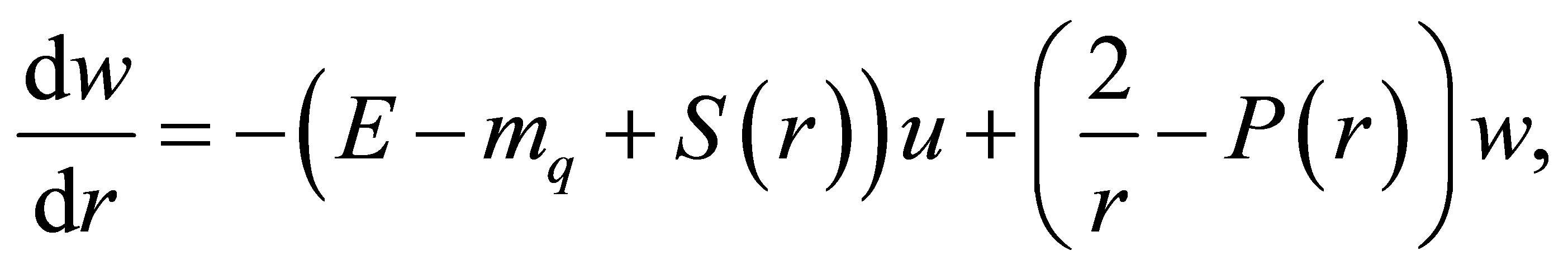 (14)
(14)
where  are the scalar potential, the pseudoscalar potential and the eigenvalue of the quark spinor
are the scalar potential, the pseudoscalar potential and the eigenvalue of the quark spinor . The set of Equations (9), (10), (13), (14) is solved following the method used by Goldflam and Wilets [20] and Birse and Banarje [4] for the Soliton Bag model. Including the color degree of freedom, one has
. The set of Equations (9), (10), (13), (14) is solved following the method used by Goldflam and Wilets [20] and Birse and Banarje [4] for the Soliton Bag model. Including the color degree of freedom, one has  where
where 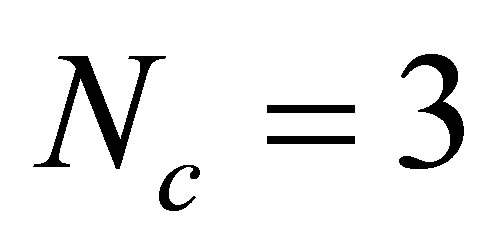 for the number of colors and g is coupling constant.
for the number of colors and g is coupling constant.
Then
 (15)
(15)
 (16)
(16)
 (17)
(17)
where ρs, ρp and ρv are the scalar density, pseudoscalar density, and vector density respectively. Finally, we have solved the Equations (13) and (14) using fourth order Rung-Kutta. Due to the implicit nonlinearly of our Equations (9) and (10) it is necessary to iterate the solution until self-consisteny is achieved (For details; see Ref. [1]) for details. To start this iteration process, we use the chiral circle form for the meson fields,
 (18)
(18)
 (19)
(19)
where
 (20)
(20)
The field Equations (9), (10), (13) and (14) are subject to the boundary conditions requiring asymptotically the fields approach their vacuum values,
 (20)
(20)
(For details; see Ref. [1]).
3. The Chiral Perturbation Theory (χPT)
The (χPT) [9] is based on an effective chiral Lagrangian describing the valence quarks of baryons as relativistic fermions moving in a self consistent field (static potential) [10]
 (22)
(22)
which are supplemented by a cloud of Goldstone bosons 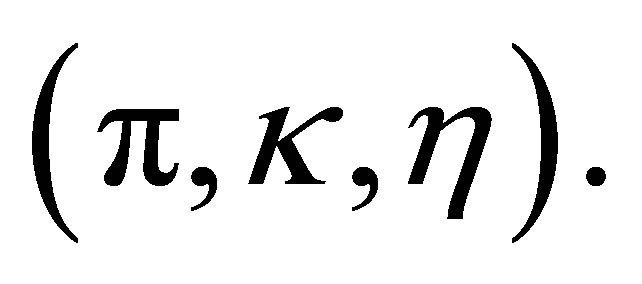 Treating Goldstone field as small fluctuations around the three quark (3q) core and derive a linearized effective Lagrangian
Treating Goldstone field as small fluctuations around the three quark (3q) core and derive a linearized effective Lagrangian . The Lagrangian
. The Lagrangian
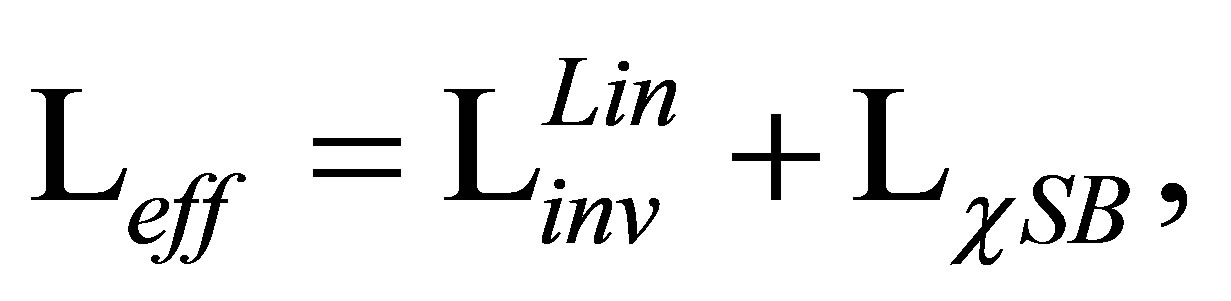 (23)
(23)
derived in Ref. [11], includes the linear chiral invariant term
 (24)
(24)
and a term  which explicitly breaks chiral symmetry
which explicitly breaks chiral symmetry
 (25)
(25)
Containing the mass term for quarks and mesons[11]. The octet matrix  of pseudoscalar mesons is defined as:
of pseudoscalar mesons is defined as:
 (26)
(26)
F is the pion decay constant [11] in chiral limit;
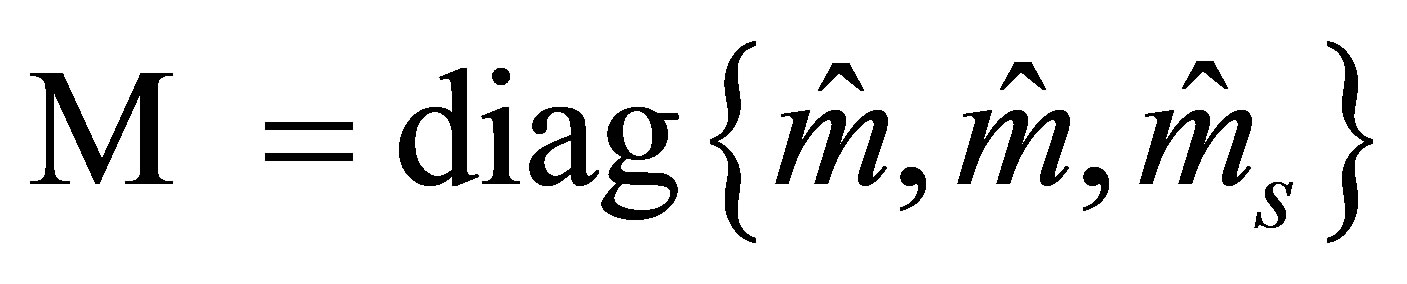 (27)
(27)
is the mass matrix of current quarks (we restrict to the isospin symmetry limit with ; B =
; B =
 is the low-energy constant which measurs the vacuum expectation value of the scalar quark densities in the chiral limit [12]. We rely on the standard picture of chiral symmetry breaking [14] and for the masses of pseudoscalar mesons we use the leading term in their chiral expansion (i.e. linear in the current quark mass):
is the low-energy constant which measurs the vacuum expectation value of the scalar quark densities in the chiral limit [12]. We rely on the standard picture of chiral symmetry breaking [14] and for the masses of pseudoscalar mesons we use the leading term in their chiral expansion (i.e. linear in the current quark mass):
 (28)
(28)
Meson masses obviously satisfy the Gell-MannOakes-Renner Equation (13) and the Gell-Mann-Okubo relation . In the evaluation, we use the following set of QCD parameters [13]:
. In the evaluation, we use the following set of QCD parameters [13]:
 ,
,
 and
and .
.
To derive the properties of baryons, which are modelled as bound states of valence quarks surrounded by a meson cloud, we formulate perturbation theory. At zeroth order, the unperturbed Lagrangian simply describes the nucleon by three realativistic valence quarks which are confined by the effective one-body potential in the Dirac equation. The mass  of the three-quark core of the nucleon is then related to the single quark ground state energy
of the three-quark core of the nucleon is then related to the single quark ground state energy  by
by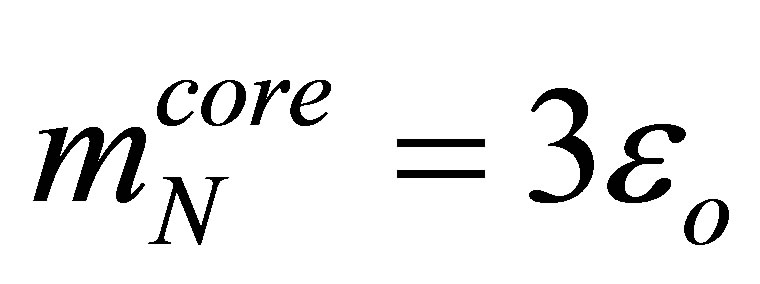 .
.
4. Results and Conclusion
The field Equations (9), (10), (13) and (14) have been solved by iteration for different values of quark and sigma masses. The dependences of the nucleon properties on the sigma and quark masses are listed in Tables 1 and 2 that show the nucleon observables which have been calculated for the values in the range of 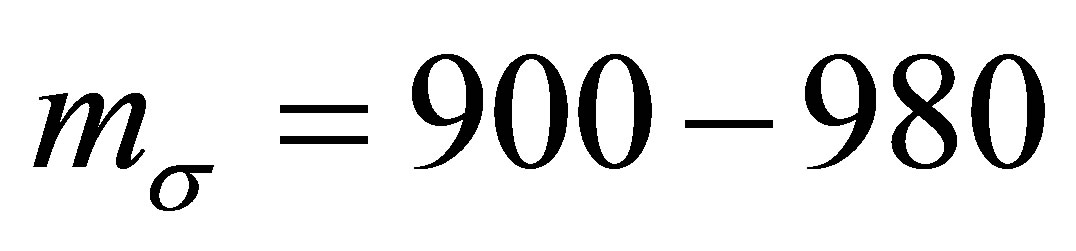 MeV and
MeV and  MeV. It is seen from Table 1 that as sigma mass increases, all the nucleon observables decrease and then get closer to the experimental data, except the nucleon magnetic moments. In fact, neither
MeV. It is seen from Table 1 that as sigma mass increases, all the nucleon observables decrease and then get closer to the experimental data, except the nucleon magnetic moments. In fact, neither  nor
nor 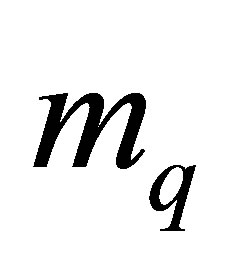 is experimental data, since the quark cannot be isolated (due to the confinement principle), we believe
is experimental data, since the quark cannot be isolated (due to the confinement principle), we believe  is of order of one third of the nucleon mass and from Nambu and Jona-Lasinio model [6],
is of order of one third of the nucleon mass and from Nambu and Jona-Lasinio model [6],  is twice
is twice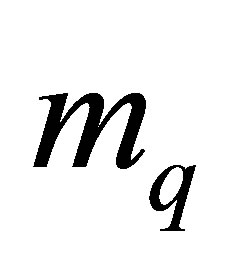 . The experimental values of the pion decay coupling constant and the pion mass are 93 MeV and 139.6 MeV respectively, but by decreasing these values following Hemmert et al. [21] to the values 91.9 MeV and 138.04 MeV, all the nucleon observables decrease. I assume here the value of the constituent quark mass to have a range of 370 - 440 MeV depending on the model parameters. In
. The experimental values of the pion decay coupling constant and the pion mass are 93 MeV and 139.6 MeV respectively, but by decreasing these values following Hemmert et al. [21] to the values 91.9 MeV and 138.04 MeV, all the nucleon observables decrease. I assume here the value of the constituent quark mass to have a range of 370 - 440 MeV depending on the model parameters. In

Table 1. Values of magnetic moments, σ (πN) and gA (0) at mq = 400 MeV. All quantities in MeV.

Table 2. Values of magnetic moments, σ (πN) and gA (0) at mq = 1000 MeV. All quantities in MeV.
some schematic way, the LSM and the hedgehog projection techniques are valid only for a very small number of pions (about 0.5 and less), and the LSM was better (in a variational sense) than the ordinary hedgehog. The generalized hedgehog appears always to be the best. Unfortunately, none of the above approaches yields a proper axial vector coupling constant of 1.25 nor a proper pionnucleon sigma term (whose present day value with all corrections of the Bern group is (45 ± 5)). The results of Ref. [17] were successfully applied to the study of sigma-term physics, and those results for the  sigma term
sigma term 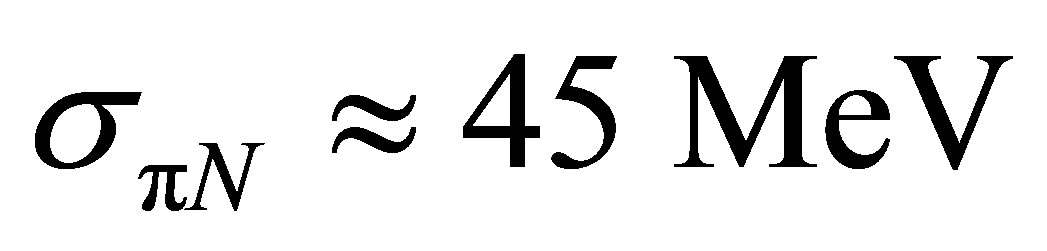 are in a good agreement with the value deduced by [18] using dispersion-relation techniques and exploiting the chiral symmetry constraints. To achive these goals, one should not, as we believe, replace the whole system by a boson field (as Skyrme does) nor replace the Dirac Sea by a boson field (as the above approaches do). An approach (simple quark model) [22] considers the simple quark model in the limit of SU (3) flavor symmetry at the strange quark mass. The approach gives an excellent fit for the octet baryon magnetic moments (see Table II in Ref. [22]). They obtained μp = 2.724 and μn = −1.826 which are in very good agreements with the experimental results μp = 2.793 and μn = −1.913 that are better than LSM. However, the rest of the properties of the nucleons have not been calculated in this model. The idea represented in this approach [22] leads to a new appreciation of the role of the consistuent quark model in modern hadron phenomenology in which there is no longer a conflict with the constraints of (χPT). So far, all these approaches do not produce the three known properties in QCD, namely confinement, chiral symmetry and asymptotic freedom. We hope that the ideas presented here will lead to a new combined approach which successfully agrees with the three main
are in a good agreement with the value deduced by [18] using dispersion-relation techniques and exploiting the chiral symmetry constraints. To achive these goals, one should not, as we believe, replace the whole system by a boson field (as Skyrme does) nor replace the Dirac Sea by a boson field (as the above approaches do). An approach (simple quark model) [22] considers the simple quark model in the limit of SU (3) flavor symmetry at the strange quark mass. The approach gives an excellent fit for the octet baryon magnetic moments (see Table II in Ref. [22]). They obtained μp = 2.724 and μn = −1.826 which are in very good agreements with the experimental results μp = 2.793 and μn = −1.913 that are better than LSM. However, the rest of the properties of the nucleons have not been calculated in this model. The idea represented in this approach [22] leads to a new appreciation of the role of the consistuent quark model in modern hadron phenomenology in which there is no longer a conflict with the constraints of (χPT). So far, all these approaches do not produce the three known properties in QCD, namely confinement, chiral symmetry and asymptotic freedom. We hope that the ideas presented here will lead to a new combined approach which successfully agrees with the three main

Table 3. Values of the observables calculated from the chiral perturbation theory (χPT) are compared with our calculations using the linear sigma model (LSM).
observations of QCD. We found quark and sigma masses affected observables of nucleon as seen from Tables 1 and 2. Finally, we compare our model with experimental data and the χPT in Table 3.