Limited Bandwidths and Correlation Ambiguities: Do They Co-Exist in Galileo Receivers ()
1. Introduction
New advances in the field of satellite positioning and the design of new satellite systems to be used for location purposes in the years to come created the need for new modulation and signal types at the transmitter side. The upcoming satellite systems, such as the European Galileo and Chinese Compass systems, need to preserve compatibility with the existing Navstar GPS system, while keeping the interference levels at minimum. This motivated the introduction of a w modulation family, namely the Binary Offset Carrier (BOC) family, which currently have several variants, such as sine BOC [1-3], cosine BOC [3,4], alternate BOC (AltBOC) [5,6], Composite BOC (CBOC) [7,8], and Time Multiplexed BOC (TMBOC) [8]. BOC-modulated signals are split-spectrum signal, where the energy peak is not located anymore at the carrier frequency, such as for the classical Binary Phase Shift Keying (BPSK) modulation. The energy lobe is split into two symmetrical lobes, spaced at a certain, adjustable, distance from the carrier frequency. The spacing is determined in fact by the sub-carrier rate fsc used in these split-spectrum modulations. As a consequence of the spectrum splitting, the Auto-Correlation Envelope (ACE) of these signals has also different properties compared with the BPSK case. Two main consequences have been noticed in the literature with respect to the new ACE: on one hand, notches in the ACE shape appear within +/–1 chip interval, which introduces some challenges in the acquisition process [9] and on the other hand, the main lobe of the ACE is narrower than for BPSK modulation, which might bring benefits in tracking [7,8]. The focus in this paper is on the acquisition stage, which is the most demanding in terms of hardware and/or power consumption. Typically, in order to deal with the notches (or ambiguities) of the ACE, some unambiguous methods can be used, in which the goal is to recreate a BPSK-like shape [1,9-15]. However, all these unambiguous methods have been analyzed so far only under the assumption of infinite or very large receiver bandwidths. For mass-market receivers, it is however important to be able to reduce the front-end filter bandwidth. The question we address in this paper is how such a bandwidth limitation will affect the signal correlation shapes and whether there is still need for unambiguous processing. This question has not been addressed before to the best of the Author’s knowledge. The novel contributions of this paper are:
• A thorough analysis of the ambiguities in the BOC/ CBOC correlation functions, in the presence of limited receiver bandwidth, ranging from 3 MHz (severe limitation, narrowband receiver) to 24.552 MHz (bandwidth used in the Galileo specifications [16], wideband receivers).
• An explanation based on semi-analytical model regarding the fact that a limited front-end receiver bandwidth acts as an ‘unambiguous method’, by reducing the ambiguities in the correlation function, and thus removing the need for a supplementary unambiguous processing.
Additionally, an overview of unambiguous methods and a generic block diagram for them is offered in the context of split-spectrum modulations, and design recommendations for Galileo E1 receiver acquisition architecture are done.
2. Correlation Ambiguity Problem and State-of-Art Solutions
The CBOC and AltBOC modulations used in Galileo split the signal spectrum into two symmetrical components around the carrier frequency, by multiplying the pseudorandom (PRN) code with a rectangular sub-carrier. This spectrum splitting is seen also as a splitting in the correlation domain, meaning that the correlation function envelope will exhibit additional sidepeaks (besides the main correlation peak) and additional low values within +/–1 chip interval from the main peak. These low values (or notches) in the correlation function are typically referred to as ambiguities, as illustrated in Figure 1.
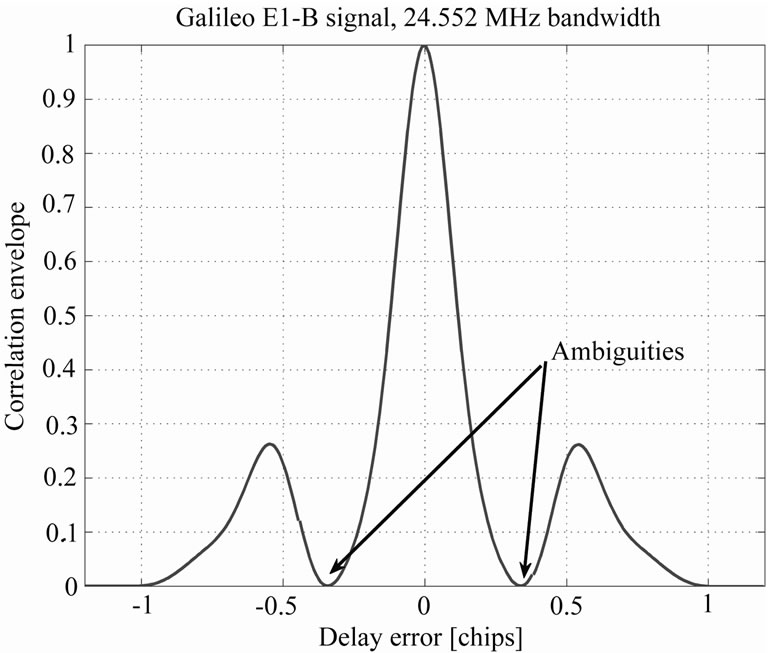
Figure 1. Illustration of the ambiguities in a CBOC (+) modulated signal with 24.552 MHz double-sided front-end bandwidth.
These ambiguities create problems in the acquisition process, in the sense that, if a too high time-bin step is used, we might lose the main correlation peak, as illustrated in Figure 2, for a time-bin step  of 0.5 chips and for E1-B signal with 24.552 MHz double-sided bandwidth. The acquisition samples are the outputs of the correlator unit. These acquisition samples are to be used as input to the decision unit. The step between two successive tentative delays is
of 0.5 chips and for E1-B signal with 24.552 MHz double-sided bandwidth. The acquisition samples are the outputs of the correlator unit. These acquisition samples are to be used as input to the decision unit. The step between two successive tentative delays is , expressed in chips. It is seen in Figure 2, that the maximum peak can be missed if we use a 0.5 chip time-bin step, which will have drastic repercussions on the detection probability in the acquisition stage.
, expressed in chips. It is seen in Figure 2, that the maximum peak can be missed if we use a 0.5 chip time-bin step, which will have drastic repercussions on the detection probability in the acquisition stage.
One solution is to diminish the time-bin step (to values lower than half of the main correlation lobe width), at the expense of a larger acquisition time, since more time bins need to be tested. Another solution is to modify the ambiguous correlation into an ‘unambiguous’ one, via frequency-domain or time-domain processing, as explained for example in [13-15] and illustrated in the generic block diagram of Figure 3. The explanation of the different blocks in Figure 3 is given below, according to the unambiguous method that is used.
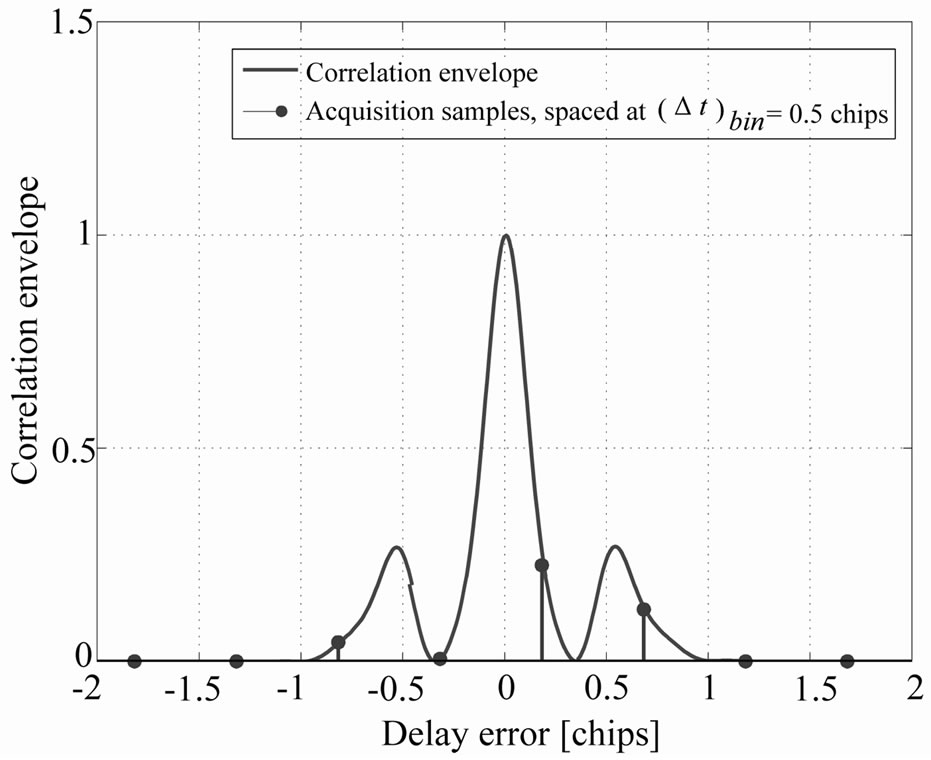
Figure 2. Ambiguity problem in acquisition for large timebin steps (here  chips. CBOC (+) modulation.
chips. CBOC (+) modulation.
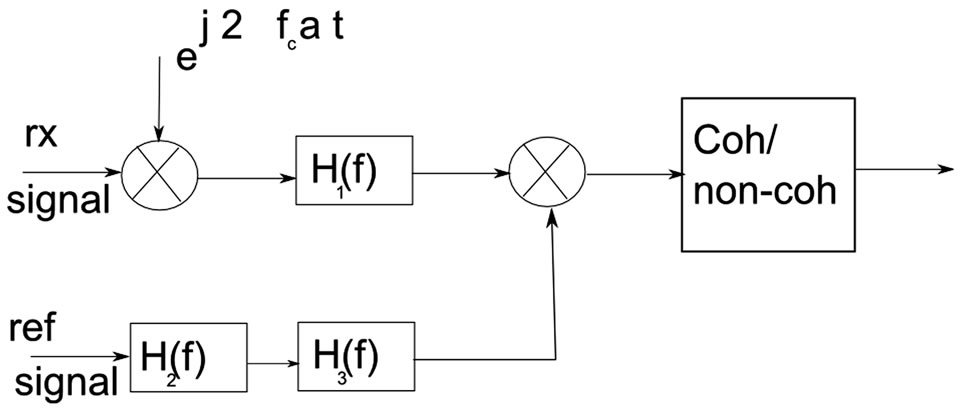
Figure 3. Generic block diagram for unambiguous acquisition methods; single-sideband concept.
An overview of the state-of-art unambiguous acquisition methods in Galileo is as follows:
1) B&F methods, denoted as such after the initial of the first authors who introduced them in [1,10]; in here, only the upper or the lower sideband of the received signal is filtered and correlated with a similarly filtered reference modulated code. Both upper and lower sidebands can be then combined non-coherently (dual-band processing) or only one of the sidebands can be used (single sideband processing). The single-sideband block diagram is illustrated in Figure 3, where the following parameters and filters are used: a = 0 (i.e., no shifting stage), H1(f) = H3(f) = upper/lower lobe selection filters, applied both on incoming signal and reference modulated code, and H2(f) = 1.
2) mM\&H methods, denoted as such after the initial of the first authors who introduced them in [11,12]; in here, both upper and lower lobes of the signal spectrum are selected, plus everything between them. The incoming signal is shifted with a shift parameter a, which is modulation dependent, e.g., a = 1 for CBOC (details on optimum a parameters for other split-spectrum BOC modulations are given in [13]) The filters frequency responses are: H1(f) is a filter selecting both main frequency lobes of the signal, plus everything between them, H2(f) is a hold filternamely ,
,  = chip interval,
= chip interval,  = BOC interval (e.g.,
= BOC interval (e.g.,  for CBOC), and H3(f) = 1.
for CBOC), and H3(f) = 1.
3) Unambiguous Adjacent Lobe (UAL) methods, proposed by the Author in [13-15]. In here, a is the same modulation-dependent factor as used in mM\&H methods, H1(f) = H3(f) = 1 (absent filters)and  is a hold filter.
is a hold filter.
After the correlation of the incoming signal with the reference code, coherent and non-coherent integration may be applied, as shown in Figure 3. For example, in our simulations we used 4 ms coherent integration and 5 blocks non-coherent integration, which means a total integration time of 20 ms.
Then a decision variable is formed. For example, for a serial search approach, the decision variable, denoted in what follows via Z, is the non-coherent correlation output.
An example of the normalized unambiguous correlation functions after single sideband processing of a CBOC signal is shown in Figure 4. Also the ambiguous processing case (aBOC) is shown for reference purpose. In this figure, the CBOC(-) signal, as used for E1 Galileo pilot channels is processed with a sine BOC(1,1) transmitter, and the receiver double-sided bandwidth is 24.552 MHz [16].
Regarding the complexity of various unambiguous methods, a comparison has been provided in [13].
3. Receiver Acquisition Block
The focus here is on Galileo E1 Open Service signals, which employ CBOC modulation. Two CBOC variants, i.e. CBOC (+) and CBOC (-) are used currently [16]. The CBOC modulation is formed as a weighed sum (CBOC (+)) or weighted difference (CBOC(-)) of two sine BOC waveforms: a sine BOC (1,1) and a sine BOC (6,1). An analytical modeling of CBOC signals has been provided by the Author in [17]. CBOC signals can be processed either with a CBOC receiver, or with a lower-complexity sine BOC (1,1) receiver, as detailed in [18]. Basically, there are 4 variants based on CBOC signal that are considered here:
1) CBOC (+) signal at transmitter and CBOC (+) modulated reference code (e.g., full processing of Galileo E1 data channels)
2) CBOC (+) signal at transmitter and sine BOC (1,1) -modulated reference code (e.g., low complexity one-bit processing of Galileo E1 data channels)
3) CBOC (-) signal at transmitter and CBOC (-) -modulated reference code (e.g., full processing of Galileo E1 pilot channels)
4) CBOC (-) signal at transmitter and sine BOC (1,1) -modulated reference code (e.g., low complexity one-bit processing of Galileo E1 pilot channels)
The detection probabilities Pd are computed within +/–

Figure 4. Unambiguous single-sideband normalized correlation envelopes. BW = 24.552 MHz. CBOC(-) at tx and SinBOC(1,1) at rx.
0.35 chips error, based on the fact that the main correlation lobe for a CBOC-modulated signal is about 0.7 chips (i.e., if we acquire the signal with an error less than half of the main lobe, we consider that acquisition was done ‘correctly’ and we can move to the tracking stage; if the error is higher than half of the width of the main lobe, then the acquisition was unsuccessful).
Under additive white Gaussian channel assumption, it is straightforward to show, following the model of [9] that detection and false alarm probabilities can be computed based on chi-square central and non-central distributions, as follows:
 (1)
(1)
Above,  is the detection probability per bin, computed as the probability that the decision variable is higher than a decision threshold, provided that we are in a correct bin (hypothesis H1):
is the detection probability per bin, computed as the probability that the decision variable is higher than a decision threshold, provided that we are in a correct bin (hypothesis H1):
 (2)
(2)
where  is the decision statistic corresponding to the estimated code phase
is the decision statistic corresponding to the estimated code phase ,
,  is the acquisition threshold,
is the acquisition threshold,  is the true Line Of Sight (LOS) delay of the channel (expressed in chips), and
is the true Line Of Sight (LOS) delay of the channel (expressed in chips), and . The acquisition threshold is computed based on a pre-defined target false alarm probability Pfa (here, 10-3). It was assumed that the residual Doppler error
. The acquisition threshold is computed based on a pre-defined target false alarm probability Pfa (here, 10-3). It was assumed that the residual Doppler error  was 0, thus,
was 0, thus,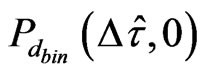
 .
.
In Equation (1)  and
and  are the Cumulative Distribution Function (CDF) under correct and incorrect-bin hypotheses, respectively, and they can be written as [9]:
are the Cumulative Distribution Function (CDF) under correct and incorrect-bin hypotheses, respectively, and they can be written as [9]:
 (3)
(3)
with  and
and  being the noise variance, number of degrees of freedom, and non-centrality parameter (dependent on signal power), and
being the noise variance, number of degrees of freedom, and non-centrality parameter (dependent on signal power), and  being the generalized Marcum-Q function. For dual sideband approaches,
being the generalized Marcum-Q function. For dual sideband approaches,  and for single sideband approaches,
and for single sideband approaches,  , with
, with  being the non-coherent integration length. The parameters
being the non-coherent integration length. The parameters  and
and  are obtained via simulations, according to the carrier-tonoise ratio level and according to the acquisition method (ambiguous or unambiguous).
are obtained via simulations, according to the carrier-tonoise ratio level and according to the acquisition method (ambiguous or unambiguous).
There can be several correct bins (denoted here as Nt), and therefore the total detection probability Pd is given by:
 (4)
(4)
that is, the sum of probabilities of detecting the signal in the i-th bin, provided that all the previous tested hypotheses for the prior correct bins gave a misdetection. In Equation (4),  is the delay error associated with the first sampling point in the two-chip interval where we have the Nt correct bins. Equation (4) is valid only for fixed sampling points. However, due to the random nature of the channels, the sampling point (with respect to the channel delay) is randomly fluctuating, hence, the global Pd will be computed as the expectation operator over all possible initial delay errors (under uniform distribution, we simply take the temporal mean):
is the delay error associated with the first sampling point in the two-chip interval where we have the Nt correct bins. Equation (4) is valid only for fixed sampling points. However, due to the random nature of the channels, the sampling point (with respect to the channel delay) is randomly fluctuating, hence, the global Pd will be computed as the expectation operator over all possible initial delay errors (under uniform distribution, we simply take the temporal mean):
 (5)
(5)
Figure 5 also illustrates the idea of computing the global Pd. Here, only three possible sampling sequences are shown for illustration purposes. The total number of sampling sequences depends on a discrete step, chosen sufficiently small. The step of searching the time bins in this figure is  chips.
chips.
The analysis presented here has been done semi-analytically, for serial search and single-path channel in order to find out the relative performance of various acquisition algorithms. Since the channel LOS delay is unknown, we can have several possible sequences of samples of the correlation function, as illustrated in Figure 5. Hypothesis H1 corresponds to the ‘correct acquisition’ case (i.e., samples within the main lobe of the correlation
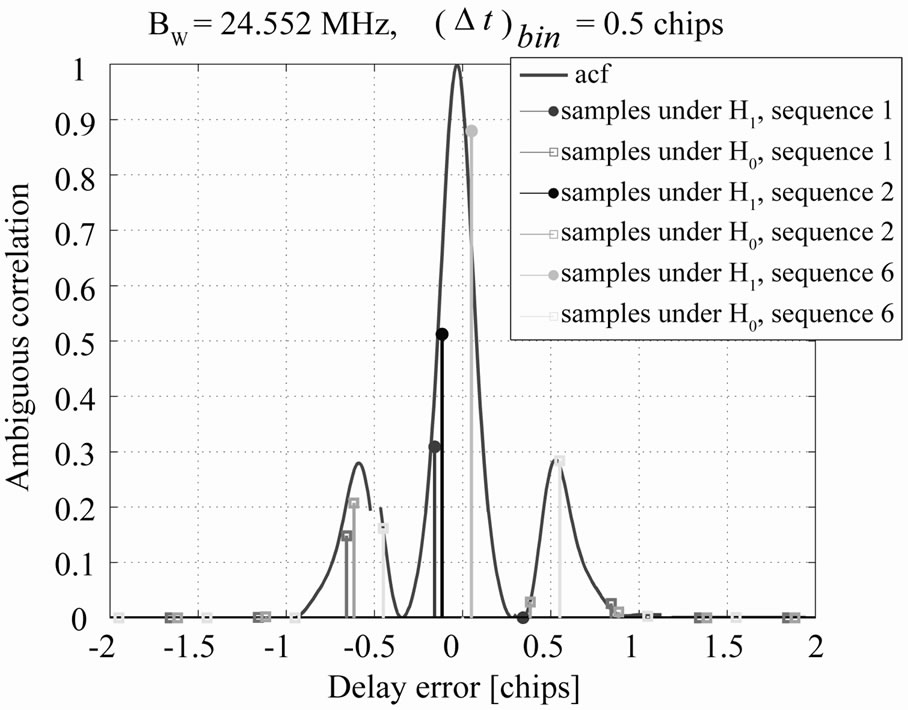
Figure 5. Illustration of the sampling sequences possibilities (according to various channel delay) for a time-bin step of 0.5 chips, 24.552 MHz double-sided bandwidth and abiguous acquisition. CBOC(+) tx with ref CBOC ( + ) rx.
envelope), and Hypothesis H0 corresponds to the ‘incorrect acquisition’ cases (i.e., samples outside the main lobe).
4. Behaviour under Limited Front-End Bandwidths
For a severe receiver front-end bandwidth limitation, for example 3 MHz, the correlation shapes with ambiguous and unambiguous processing are highly modified (see Figure 6) compared with the large bandwidth situation (see Figure 7).
If we compare Figure 4 with Figure 6, we see that band limitation already acts in a way like an unambiguous approach, that is it extends the main lobe correlation width (e.g., from about 0.7 chips for 24.552 MHz bandwidth to about 1.4 chips at 3 MHz bandwidth). This is one reason for which unambiguous approaches do not have any benefit at low front-end bandwidths, as it will be shown in the next section, and this is the main novel finding in our studies. It is also visible from Figure 6 that B&F unambiguous methods have very poor performance in terms of correlation shape at such low bandwidths. This will be later visible also in the detection probabilities curves.
4.1. Narrowband Receiver
4.1.1. Large Time-Bin Steps
Figure 7 shows the detection probabilities for a large time-bin step of  chips and for BW = 3 MHz double-sided bandwidth. As seen in both figures, ambiguous average detection probability is always better than unambiguous approaches in this case. These figures are for a CBOC (-) tx with sine BOC (1,1) rx. Similar plots were obtained for the other 3 combinations, and are not reproduced here due to overlapping findings.
chips and for BW = 3 MHz double-sided bandwidth. As seen in both figures, ambiguous average detection probability is always better than unambiguous approaches in this case. These figures are for a CBOC (-) tx with sine BOC (1,1) rx. Similar plots were obtained for the other 3 combinations, and are not reproduced here due to overlapping findings.
4.1.2. Small Time-Bin Steps
Figure 8 and Figure 9 show the detection probabilities (average  and worst case
and worst case ) for a small timebin step of
) for a small timebin step of  chips and for BW = 3 MHz double-sided bandwidth. UAL and mM\&H algorithms are perfectly overlapping. The differences between worst-case and average case detection probabilities for ambiguous, mM\&H and UAL cases are very small (less than 0.01 dB) and therefore they are not distinguishable in Figure 8. This is because of the main lobe width is enlarged at low bandwidth (compared with infinite bandwidth case), as already shown in Figure 6 and therefore it is less likely to have sequences with notches (or low values) for correct acquisition (H1 hypothesis). As already mentionedin the discussion related to Figure 6, B&F approach fails to work under this low bandwidth assumption, due to a highly distorted correlation function. Basically, this result points out toward the fact that sidelobe filtering in frequency domain (for unambiguous processing) is not beneficial when there is already a severe bandwidth limitation coming from the front-end receiver. B&F methods have not been studied before under low bandwidth assumption case. Under higher bandwidth, such as described in Section B, B&F methods have very good performance, as already reported in the literature [1,10,13].
chips and for BW = 3 MHz double-sided bandwidth. UAL and mM\&H algorithms are perfectly overlapping. The differences between worst-case and average case detection probabilities for ambiguous, mM\&H and UAL cases are very small (less than 0.01 dB) and therefore they are not distinguishable in Figure 8. This is because of the main lobe width is enlarged at low bandwidth (compared with infinite bandwidth case), as already shown in Figure 6 and therefore it is less likely to have sequences with notches (or low values) for correct acquisition (H1 hypothesis). As already mentionedin the discussion related to Figure 6, B&F approach fails to work under this low bandwidth assumption, due to a highly distorted correlation function. Basically, this result points out toward the fact that sidelobe filtering in frequency domain (for unambiguous processing) is not beneficial when there is already a severe bandwidth limitation coming from the front-end receiver. B&F methods have not been studied before under low bandwidth assumption case. Under higher bandwidth, such as described in Section B, B&F methods have very good performance, as already reported in the literature [1,10,13].
In Figure 9, a comparison between SSB and DSB processing is also given for references. Only UAL method has been included here, since it gave the best results
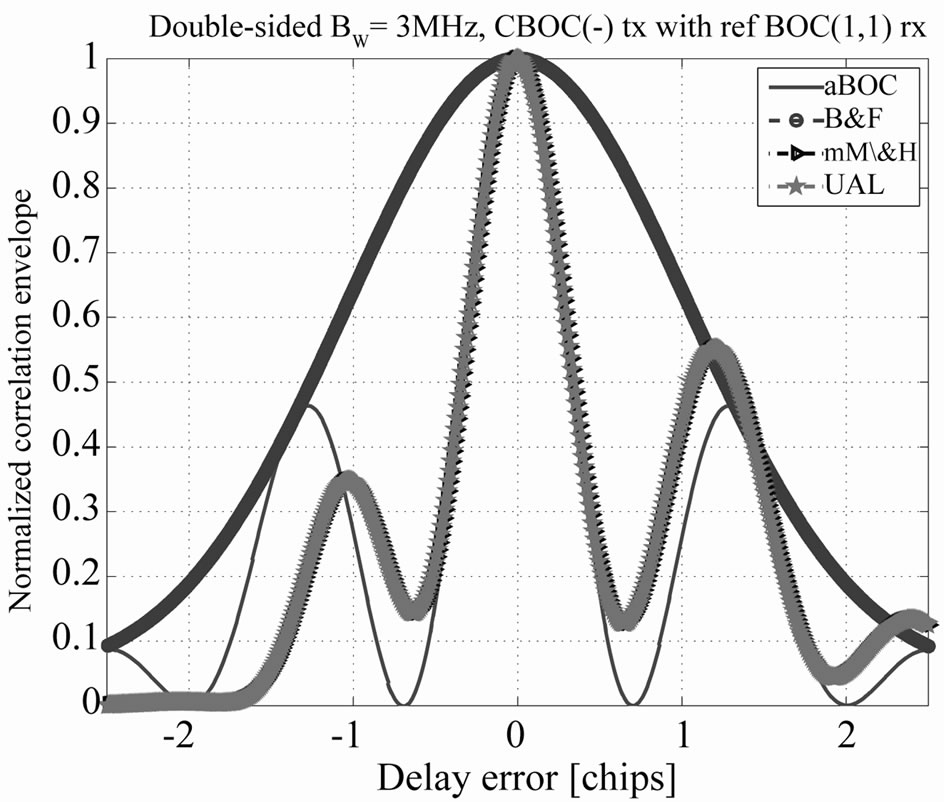
Figure 6. Unambiguous single-sideband normalized correlation envelopes. BW = 3 MHz. CBOC (-) at tx and SinBOC (1,1) at rx.
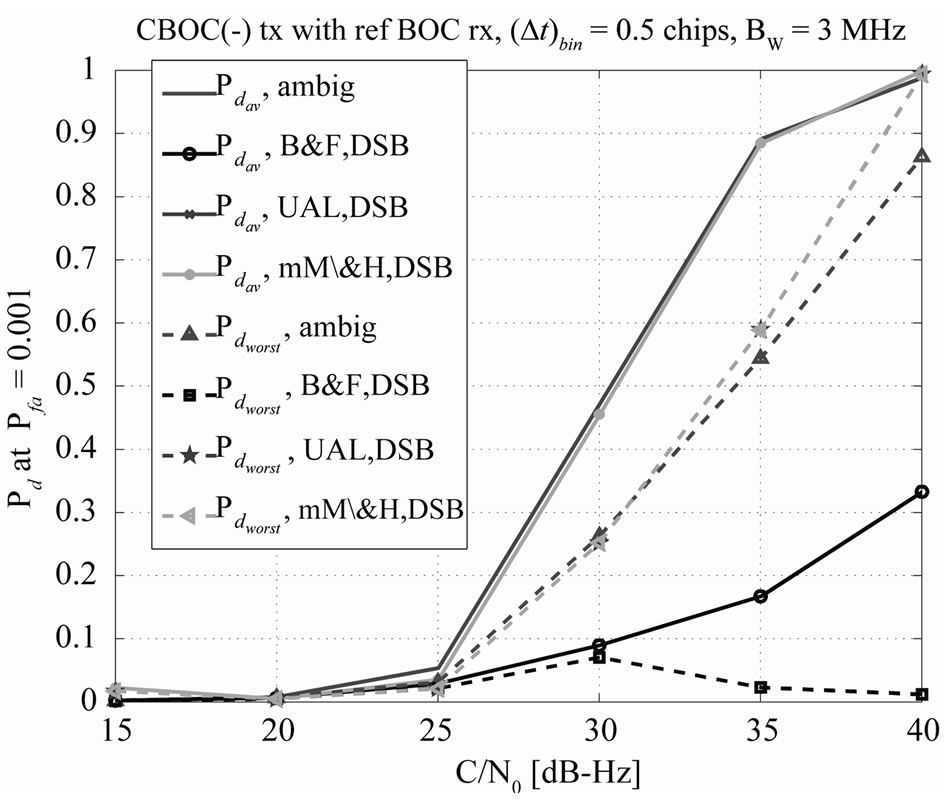
Figure 7. Comparison of single sideband with dual sideband acquisition methods (here UAL and mM\&H curves are overlapping). BW = 3 MHz,  chips.
chips.
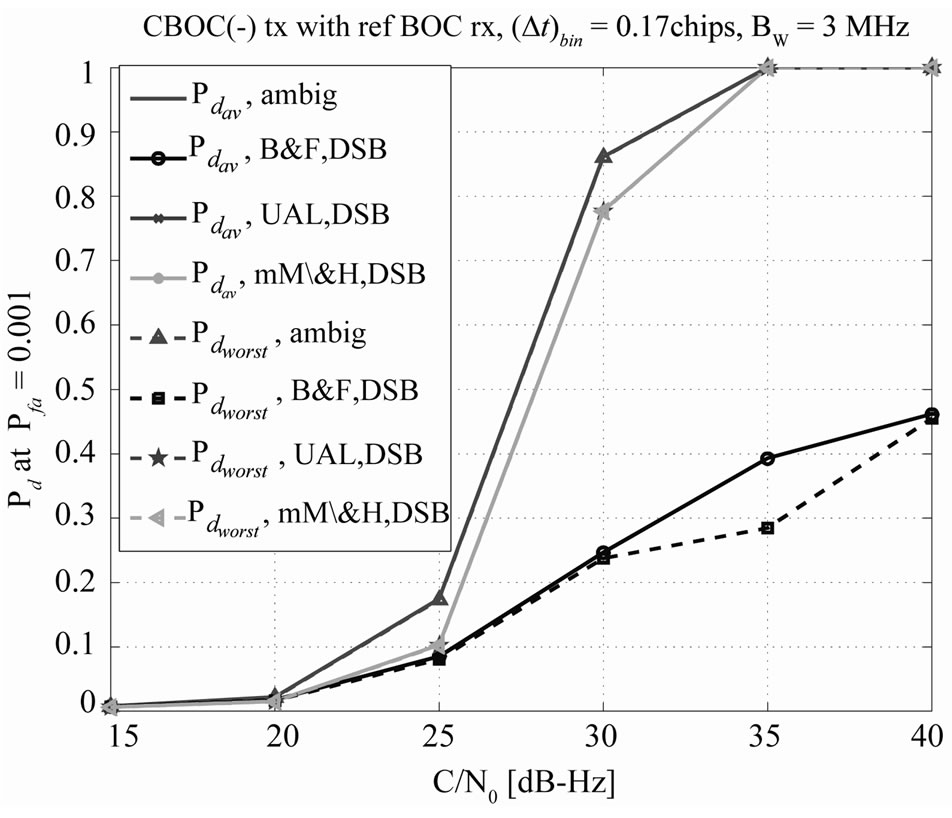
Figure 8. Comparison of ambiguous with DSB unambiguous dual sideband acquisition methods. BW = 3 MHz, 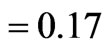
 chips (here UAL and mM\&H curves are overlapping).
chips (here UAL and mM\&H curves are overlapping).
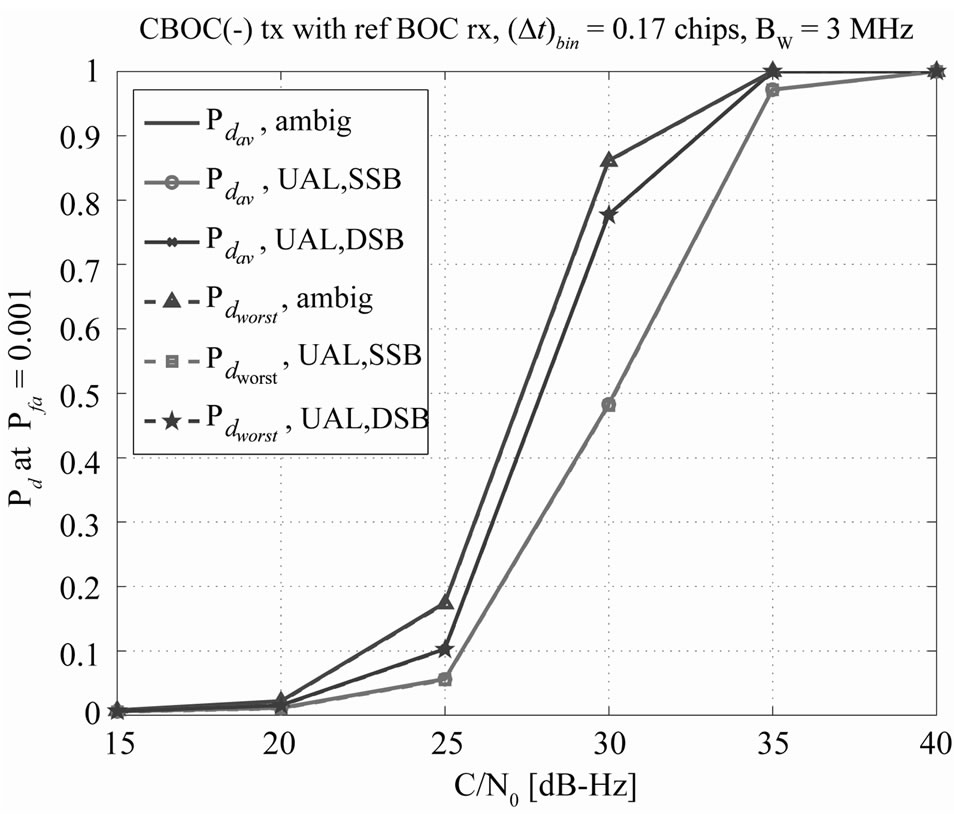
Figure 9. Comparison of single sideband with dual sideband acquisition methods. BW = 3 MHz,  chips.
chips.
among the unambiguous methods, at low receiver bandwidths. DSB stands for dual sideband processing, and SSB stands for single sideband processing.
4.1.3. Performance Versus Time-Bin Step
The dual-sideband unambiguous methods are compared with ambiguous acquisition for various time-bin steps in Figure 10.
The main conclusion based on the plots presented in this section is that unambiguous approaches bring no benefit whatsoever compared with ambiguous approaches for low receiver bandwidths, no matter on the time-bin
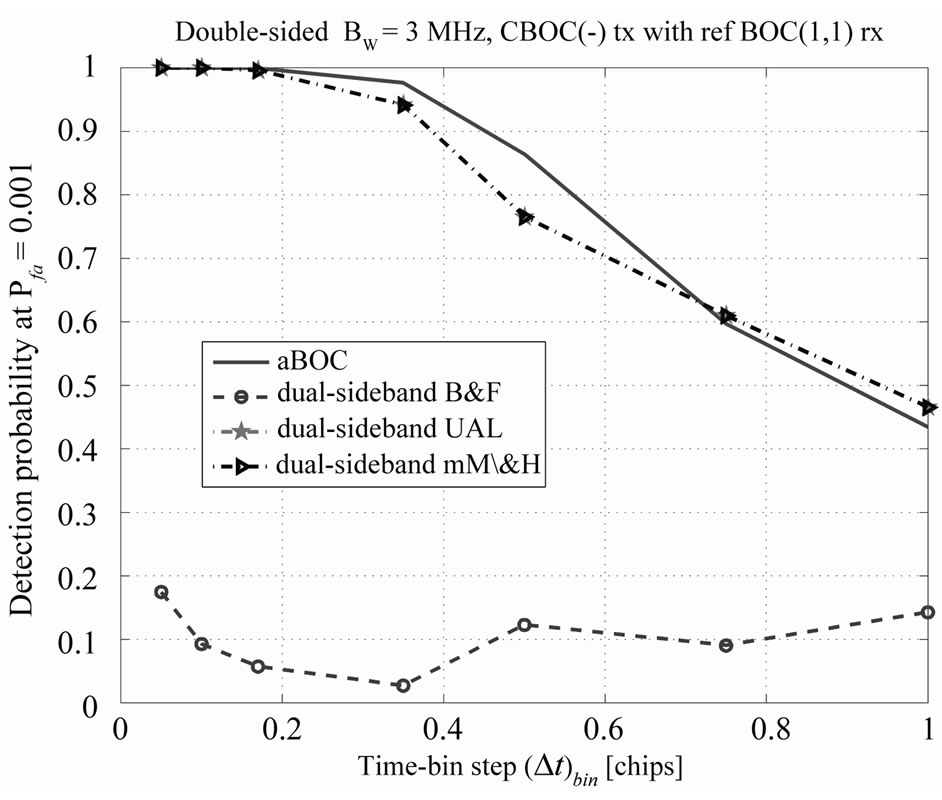
Figure 10. Detection probability versus time-bin step, at C / N0 = 35 dB-Hz and BW = 3 MHz. CBOC (-) at tx and SinBOC (1,1) at rx.
step to be used. Thus, a significant bandwidth limitation already acts as an ‘unambiguous’ method.
4.2. Wideband Receiver
4.2.1. Large Time-Bin Steps
Figures 11 and 12 are for a large time-bin step of 
 chips and for BW = 24.552 MHz doublesided bandwidth. For large time-bin steps (e.g., 0.5 chips), there is a clear gap between worst-case and average-case detection probabilities, and this gap is the highest for the ambiguous case. In fact, in the ambiguous case we can fail to detect the signal completely if the combination between sampling sequence and channel delay is a ‘bad’ combination. The unambiguous approaches for high front-end bandwidths and high time-bin steps bring indeed a significant enhancement over ambiguous ones, especially if we consider the worst-case detection probabilities. In Figure 11, the average probabilities for B&F and mM\&H are overlapping and they provide the best results among the considered approaches. This is a result similar also to what was reported in [13] for sine BOC (1,1) signals and infinite bandwidth.
chips and for BW = 24.552 MHz doublesided bandwidth. For large time-bin steps (e.g., 0.5 chips), there is a clear gap between worst-case and average-case detection probabilities, and this gap is the highest for the ambiguous case. In fact, in the ambiguous case we can fail to detect the signal completely if the combination between sampling sequence and channel delay is a ‘bad’ combination. The unambiguous approaches for high front-end bandwidths and high time-bin steps bring indeed a significant enhancement over ambiguous ones, especially if we consider the worst-case detection probabilities. In Figure 11, the average probabilities for B&F and mM\&H are overlapping and they provide the best results among the considered approaches. This is a result similar also to what was reported in [13] for sine BOC (1,1) signals and infinite bandwidth.
4.2.2. Small Time-Bin Steps
The performance at a small time-bin step of  chips is shown in Figure 13. Based on Figure 13, we remark that there is almost no gap between average and worst cases for unambiguous methods at such a low time-bin step (e.g.,
chips is shown in Figure 13. Based on Figure 13, we remark that there is almost no gap between average and worst cases for unambiguous methods at such a low time-bin step (e.g., ) and there is a very low gap between average and worst cases for ambiguous method. Again, as observed also for large time-bin steps, under large front-end bandwidth assumption, B&F and mM\&H methods are slightly better than UAL. This comparison also shows that for low time-bin steps there is not much benefit of using unambiguous methods.
) and there is a very low gap between average and worst cases for ambiguous method. Again, as observed also for large time-bin steps, under large front-end bandwidth assumption, B&F and mM\&H methods are slightly better than UAL. This comparison also shows that for low time-bin steps there is not much benefit of using unambiguous methods.
4.2.3. Performance Versus the Time-Bin Step
The dual-sideband unambiguous methods are compared with ambiguous acquisition for various time-bin steps in Figure 14. At steps of up to about 0.17 (corresponding to a quarter of the ACE main lobe width), ambiguous acquisition performs well enough (as well as the unambiguous methods). If we desire to increase the time-bin step for a lower mean acquisition time, then unambiguous approaches, and in particular B&F and mM\&H approaches outperform significantly the ambiguous appromach.
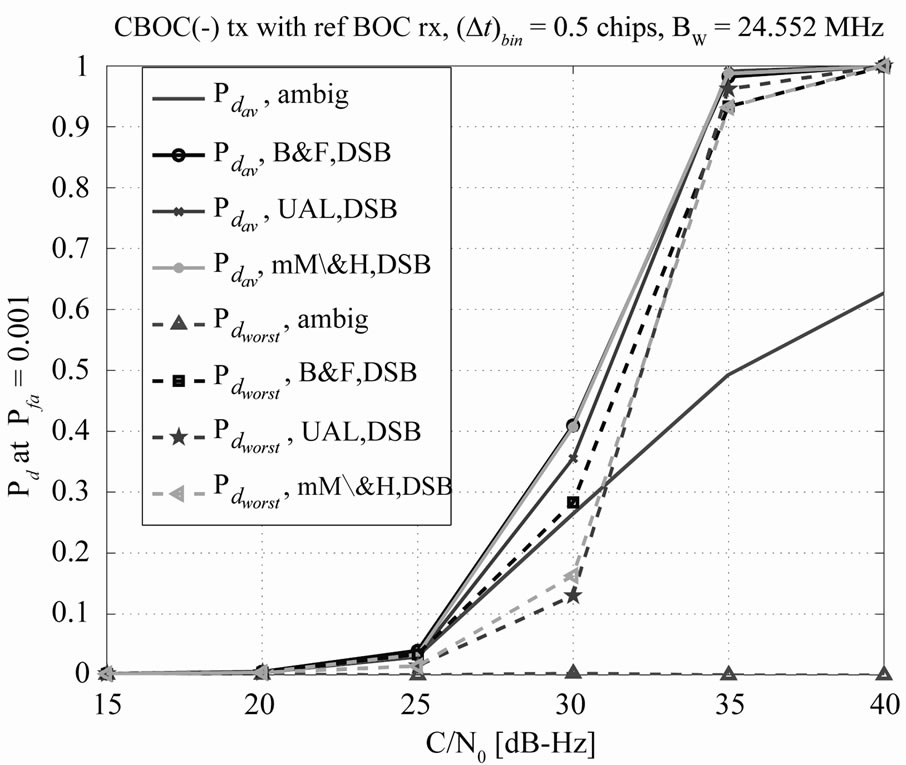
Figure 11. Comparison of ambiguous with unambiguous dual sideband acquisition methods (here B&F and mM\&H average detection probability curves are overlapping). BW = 24 MHz,  chips.
chips.
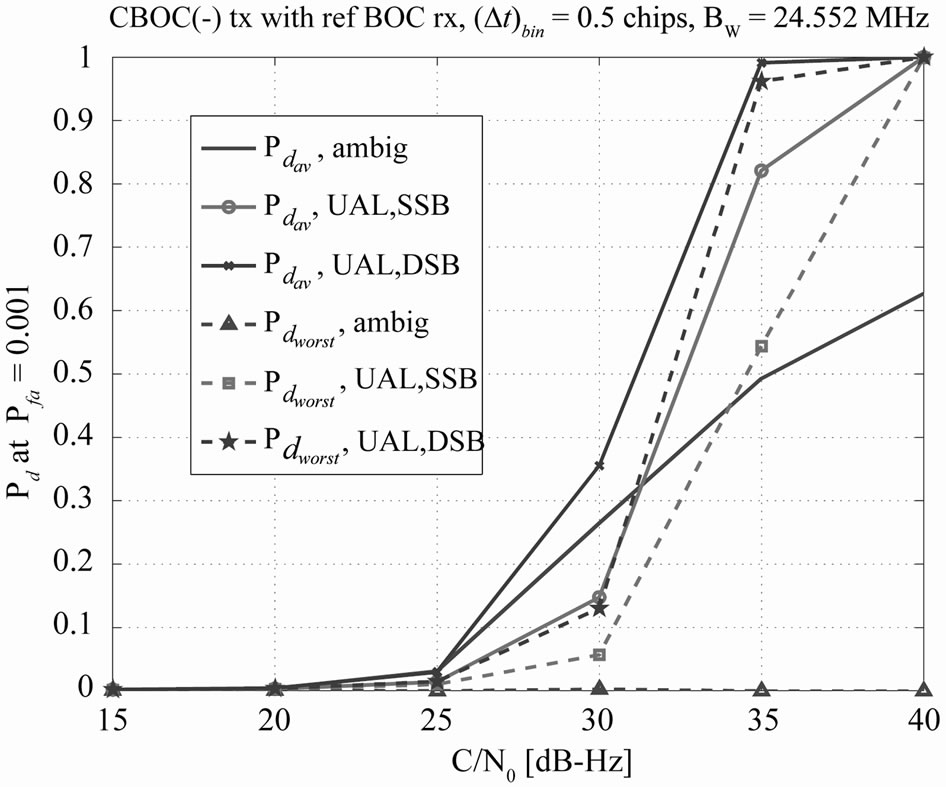
Figure 12. Comparison of single sideband with dual sideband acquisition methods. BW = 24 MHz,  chips.
chips.
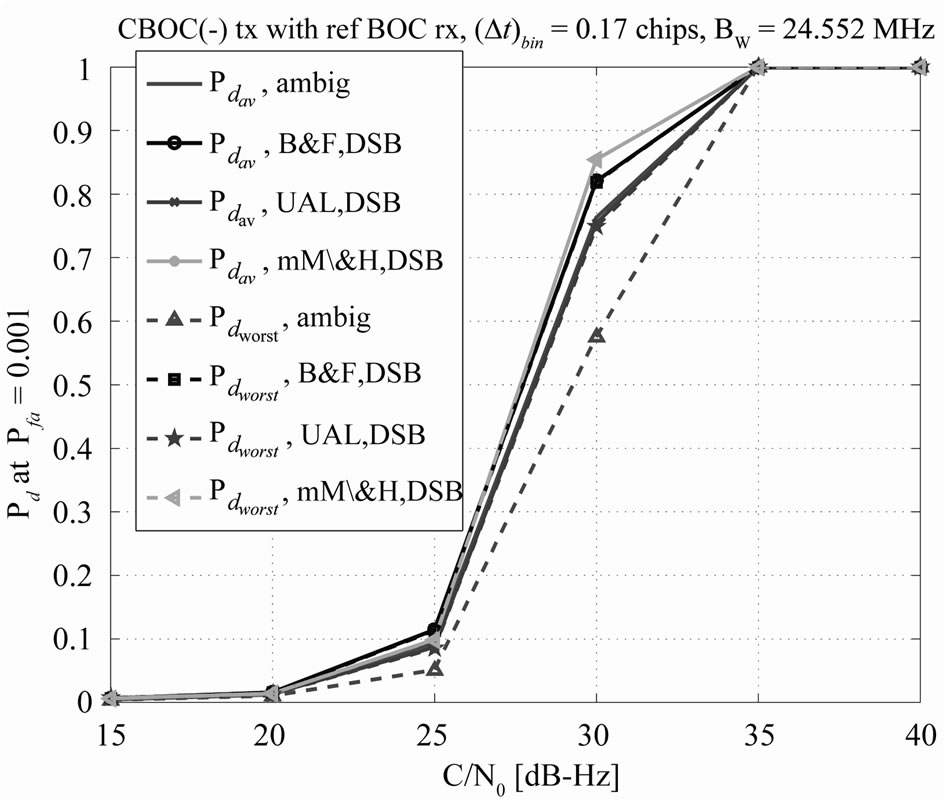
Figure 13. Comparison of ambiguous with DSB unambiguous dual sideband acquisition methods. BW = 24 MHz,  chips.
chips.
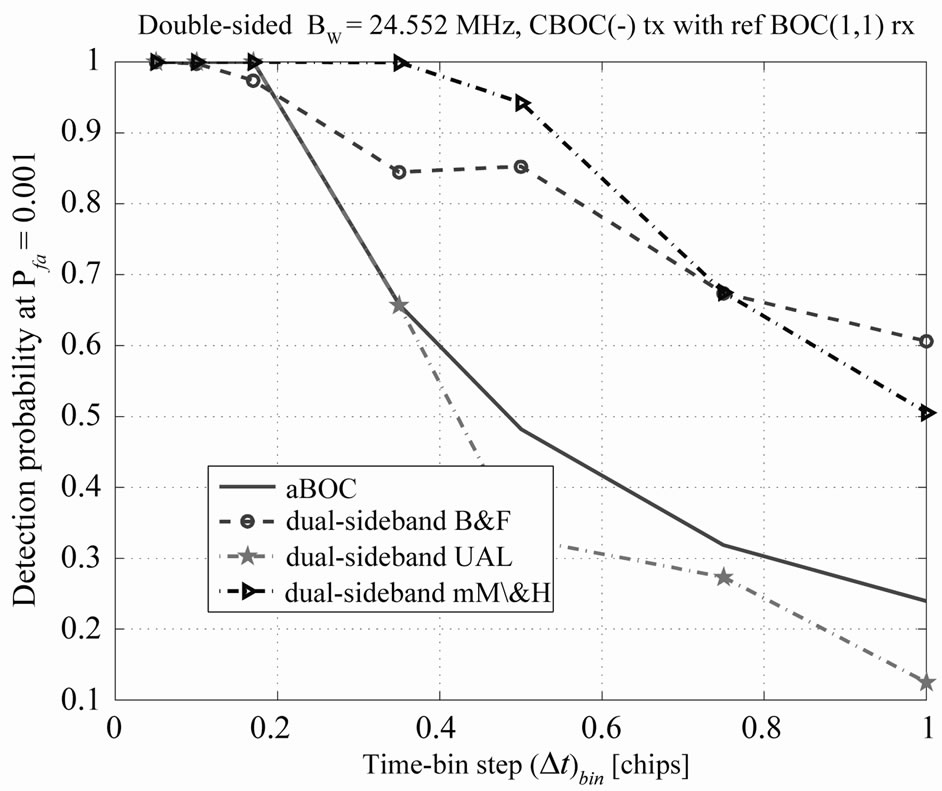
Figure 14. Detection probability versus time-bin step, at C/N0 = 35 dB-Hz and BW = 24.552 MHz. CBOC (-) at tx and SinBOC (1,1) at rx.
5. Conclusions and Recommendations
The novel finding in this paper is that, a small receiver bandwidth (e.g., 3-4 MHz double sideband, as typically used in mass-market receiver) has an inherent robustness towards the correlation ambiguities of a BOCCBOCmodulated signal and there is no need for additional unambiguous processing in such low receiver bandwidths. Therefore, for a mass-market or narrowband Galileo receiver, the recommendation is to employ the classical ambiguous correlation method in the acquisition process (no supplementary filtering or unambiguous processing) and time-bin steps of the order of 0.5 chips (in order to achieve a good tradeoff between performance and complexity).
For wideband receivers (e.g., bandwidth as specified in Galileo SIS-ICD [16]), unambiguous processing is not sufficient. In such case, the best performance is achieved with B&F unambiguous acquisition method, and similarly with the narrowband case, with a time-bin step of the order of 0.5 chips.
6. Acknowledgements
The research leading to these results has received funding from the European Union’s Seventh Framework Programme (FP7/2007-2013) under grant agreement number 227890 (GRAMMAR project). This research work has also been supported by the Academy of Finland.