1. Introduction
Among the global issues that came to the fore in the 20th century is that human impact changes the Earth’s climate, leading to global warming. The different aspects of this problem are discussed in the paper: reasons of climate changes; real possibility of ecological catastrophe because of uncontrolled greenhouse gas emissions; influence of greenhouse effect upon stable economic development.
Considering the nature of climate change there are two possible ways for humans to stabilize the surface temperature of the Earth: by regulating parameters of the absorption and reflection of solar energy. These parameters can be changed by varying not only atmospheric concentrations of greenhouse gases but also surface reflectivity. But now only regulation of concentrations of greenhouse gases is in the focus of state’s attention.
Scientists offer different solutions to the problem of distribution of quotas. Many countries (especially developing) disagree with methods of calculating quotas. Countries’ loss of implementation of obligations of reducing greenhouses gas emission is not equal. Now there is no method of calculating quotas that would suit the majority of states. Since the early 1990s numerous attempts have been made to overcome these difficulties at the international level, but none of them have been successful, mainly due to the lack of objective criteria for the solution of this problem.
This is demonstrated by the failure of negotiations on the revision of the Kyoto Protocol in Copenhagen 2009. Reducing emissions by 50% looks more like a common purpose, but not a specific obligation. Copenhagen Accord is not possible to cover developing countries. Now to revise the Kyoto Protocol international society needs new method for distribution of greenhouse gas emission.
This article presents this method. It is a mathematical algorithm of objectification of greenhouse gases distribution (on a world, a country, its region or megalopolis scale) based on the principle of differentiated responsibilities. This algorithm is a modification of the mathematical method of optimal greenhouse gases distribution published in [1-3] (Maergoiz et al., 2010, 2011).
2. The Nature of Climate Change
Let us look at the way the global surface temperature of the Earth is determined. If the Earth were an ideal blackbody, all solar energy, E, incident on the Earth’s surface would be absorbed by it and would heat it. However, the Earth is “gray”, and, thus, it reflects part of the received solar radiation back to space. The portion of solar radiation reflected by the Earth’s surface is albedo, A. Thus, the Earth is heated by energy E(l − A).
The solar-heated surface emits infrared rays into space, and their energy increases as the temperature rises, where is the Stefan-Boltzmann constant and T is the absolute temperature at the Earth’s surface. The green-house effect is caused by the emissions of the following greenhouse gases. The major contribution is made by water vapor, and this contribution keeps on growing as the temperature rises. Under the contemporary average global temperature, water vapor accounts for three-fourth of the greenhouse effect. The second place is occupied by carbon dioxide. Although carbon dioxide represents only a relatively small portion of the atmosphere, it accounts for nearly the whole of the remaining one-fourth of the green-house effect. Methane accounts for about 1% - 2%, and the contributions of all other greenhouse gases are not greater than several tenths of one percent. If there were no greenhouse gases in the Earth’s atmosphere, the global surface temperature of the Earth would be determined by the equation .
.
Due to the presence of greenhouse gases in the atmosphere, a certain amount of the energy is emitted by the Earth returns to the Earth’s surface. Thus, a firstorder approximation of thermodynamic equilibrium is described by the following equation:
 where a is the parameter determining the portion of the heat energy emitted by the Earth that is returned to the Earth’s surface by greenhouse gases.
where a is the parameter determining the portion of the heat energy emitted by the Earth that is returned to the Earth’s surface by greenhouse gases.
With the changes of the surface temperature of the Earth, the amounts of carbon dioxide and other gases remain practically unchanged. However, concentrations of atmospheric methane and water vapor (in particular) increase dramatically with a temperature rise, resulting in a so-called positive feedback. As the surface temperature of the Earth rises, the amount of atmospheric water vapor increases. The increase in the amount of atmospheric water vapor enhances the greenhouse effect and, hence, raises the surface temperature of the Earth. This process can go on until all oceans evaporate. An important part in the temperature evolution of the Earth’s surface has been played by life that emerged on the Earth (the biosphere). It began controlling concentrations of methane and carbon dioxide, removing them from the atmosphere and “hiding” them in the Earth crust, thus significantly reducing the greenhouse effect. So, the temperature on the Earth was favorable for every living thing and it evolved depending on the ratio between the carbon dioxide emitted by volcanoes and the rate of carbon sequestration inside the Earth performed by the biosphere. For the past 1.5 - 2 centuries people have been increasingly using nonrenewable fuels (coal, oil, and natural gas), thus involuntarily varying atmospheric concentrations of greenhouse gases. Additional amounts of greenhouse gases raise the Earth’s temperature, and this, in turn, increases the amount of water vapor in the atmosphere (parameter a grows) and melts the glaciers (parameter A grows). As these parameters increase simultaneously with a temperature rise, this can provoke the overheating of the Earth’s surface. The dynamic balance between the release of carbon dioxide by erupting volcanoes and its removal by the biosphere would cause alterations of warm and cold climates. This, however, does not mean that a warmer climate would be more favorable for humanity today, as both human civilization and all warm-blooded animals would lose rather than gain.
There are two possible ways for humans to stabilize the surface temperature of the Earth: by regulating parameters A and a (the greenhouse effect) in the atmosphere and on the Earth. A and a can be changed by varying not only atmospheric concentrations of greenhouse gases but also surface reflectivity—by changing the amount of clouds at different heights. This idea was first proposed in the 20th century [4] (Budyko, 1969). This approach to controlling the surface temperature of the Earth actually develops Vernadsky’s idea of the noosphere, as applied to issues of local and global climate control [5] (Vernadsky, 1998).
3. Climate Change and Sustainable Development
We can reduce our interference in natural processes by maintaining the contemporary state of the atmosphere. The arguments presented in Section 1 suggest the following dilemma: on the one hand, emissions of greenhouse gases (carbon dioxide) due to combustion of nonrenewable energy sources have to be considerably reduced. On the other hand, total energy production should be increased in order to maintain and improve the quality of life in developed countries and, what is even more important, to provide an opportunity for developing countries to attain a comparable standard of living. In order to reduce emissions of greenhouse gases due to combustion of carbon fossil fuel, both its percent in the energy budget and its actual amount should be decreased, by replacing it with renewable sources of carbon fuel, wind power, water power, and nuclear energy. It should be remembered, though, that the use of alternative energy sources will directly or indirectly increase the cost of power generation and, according to UNESCO estimates, must decrease the GDP by 1 - 2. An important consideration is that the effect of this “loss” on developed and developing countries will be different: the use of alternative energy sources can delay the achievement of high life quality in developing countries for decades.
Let us discuss various ways to solve this problem. The first was proposed by Dirk Solte [6] (Solte, 2009). The simplest, most democratic, and “equitable” way to switch from the contemporary levels of emissions to the levels of emissions equal to the threshold V, at which the effect of humans on the global temperature becomes actually imperceptible, is to set a quota, V:N, where N is the global human population. The quota for each country is proportional to its population: (V:N)n, where n is the population of a given country. The difference between the actual level of emissions and the quota for a country may be either positive or negative. If this difference is positive, the country will have to buy quotas from the countries that have a negative difference (industrially undeveloped countries emit much smaller amounts of greenhouse gases than their quota allows). The proposed algorithm allows a nearly instant attainment of the maximal level of greenhouse gas emissions necessary for the stabilization of the global temperature, and the countries are divided into three categories: the countries that buy quotas (developed countries), the counties that gradually reduce the amount of the quotas they sell (developing countries), and those preferring to live off the environmental endowment (selling the same or increased amounts of the quotas). Although this way seems to be simple, democratic, and equitable, it is actually not simple, democratic, or equitable. The first and most significant drawback of this approach is that the expected effect is too instantaneous and, like any sudden revolution, can lead to numerous social and international catastrophes.
The second drawback is that this algorithm does not take into account a nation’s history. Thirdly, no account is taken of the influence of geographic conditions: the quotas for the people living in high-latitude areas and for those living in the equatorial zone cannot be equal, as the former have to heat their homes and other buildings.
The second approach, whose implementation is being attempted now, is to get different countries, gradually and to a greater or lesser extent, to reduce their emissions. The countries accept these obligations voluntarily and cannot be punished for failing to carry them out. The main advantage of this approach is that it is liberal rather than radical. However, contradictions between developed and developing countries do not allow them to reach and implement the necessary agreements. Moreover, certain countries are rightfully suspected of selfishly pursuing their own political or economic aims while trying to stabilize the global temperature.
However, the main defect of this approach is the subjectivity of any of the proposed or finalized agreements. Thus, in our opinion, the most topical issue today is objectivization of the establishment of quotas.
4. The Legal Basis for the Establishment of the Quotas of Greenhouse Gas Emissions
The legal basis for international control and reduction of the human impact causing the “greenhouse effect” is currently provided by the UN Framework Convention on Climate Change accepted in 1992 [7] and an addition to it, the Kyoto Protocol adopted in 1997 [8]. One of the basic principles of the Convention is that of differentiated responsibilities. This principle states that the global nature of climate change calls for the widest possible cooperation by all countries, specifically pointing out that their participation should be determined by their capabilities. Thus, highly developed countries are supposed to take more serious measures and spend much more money than less developed ones. The principle of differentiated responsibilities also demands fairness in limitations of greenhouse gas emissions. This, however, is the greatest obstacle to the implementation of this principle. Point 2 of Article 4 of this Convention only commits the developed countries to reduce their emissions and return to their 1990 levels. Kyoto Protocol formulates these commitments more exactly, specifically defining reductions in greenhouse gas emissions: at least 5% below 1990 levels by 2012; it also stipulates definite, differentiated commitments for 39 parties to the Protocol. Kyoto Protocol specifies the commitments for one phase only— from 2008 to 2012. The issue of step-by-step reduction in greenhouse gas emissions by 2020 was discussed at the Climate Change Conference in Copenhagen in December 2009. However, the participants failed to reach an agreement on this issue. The project finally accepted at the Conference proposed a 50% reduction in global emissions below 1990 levels, without specific commitments from each country. The only advantage of this agreement may be that developing countries were also committed to measures for mitigating climate change.
Thus, international community has not reached an agreement on the amounts of emissions to be reduced as the subjective approach to determining them does not suit any country in the world.
5. A Mathematical Algorithm of Solving Problem
The problem of the distribution of greenhouse gas emissions is solved using the algorithm having tested for distribution of monetary resource in problems of collective investment management [9] (Maergoiz et al., 2006); [10] (Maergoiz et al., 2008). Subsection 4.1, 4.2 were presented in [1-3] (Maergoiz et al., 2010, 2011).
5.1. Problem Statement
Assume N (N > 2) groups of greenhouse gas emitters (on the global scale, in a country, a region, a megalopolis) negotiate on a certain admissible quantity V of greenhouse gas emissions (in weight units) during a fixed time period. Concentrate on the problem of the distribution of this value among all groups of emitters taking into consideration the size of the population in every group. In mathematical terms this is sum partitioning of the value
 (1)
(1)
where Vk is an admissible quantity of emissions for the group with number k. Let Sk be population of the same group, 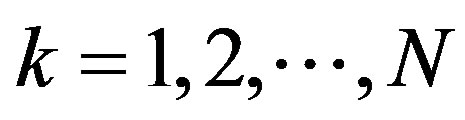 , and
, and

be population of all groups. Denote by ,
,  the mean value (density) of emissions per capita of all population and for the group with number k, where
the mean value (density) of emissions per capita of all population and for the group with number k, where , respectively. By (1), it follows the relation
, respectively. By (1), it follows the relation

Introduce the dimensionless values  (part of population in the group with number k),
(part of population in the group with number k),  (coefficient of proportionality),
(coefficient of proportionality), . Then taking into account the previous equality we find
. Then taking into account the previous equality we find
 ,
,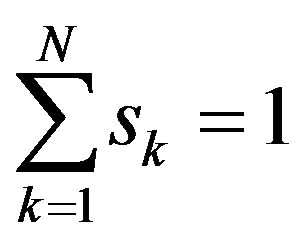 (2)
(2)
Suppose that emitters reach to the following agreement: conditional rating of every group is defined by the value of the corresponding coefficient of proportionality. Moreover, taking into consideration the principle of differentiated responsibilities for climate change, climate groups differ from each other by the introduced rating, and group indexing is given in ascending order of this value, e.g.
 (3)
(3)
here inequality  implies that n groups for n < N agree that their value (density) of emissions per capita of population be less than the mean density r. Mathematical approach to the choice of coefficients is based on the following extremal problem.
implies that n groups for n < N agree that their value (density) of emissions per capita of population be less than the mean density r. Mathematical approach to the choice of coefficients is based on the following extremal problem.
Problem B. It is necessary to find values of parameters , such that the functional
, such that the functional
 (4)
(4)
attains the minimum provided that equality (2) holds and the following additional linear relation between coefficients is fulfilled:
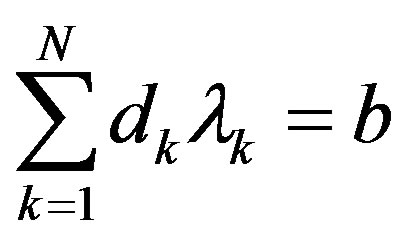 , (5)
, (5)
Parameters (see (2)) ,
,  , b are fixed numbers satisfying natural restrictions ensuring the condition: the inequality (3) is true.
, b are fixed numbers satisfying natural restrictions ensuring the condition: the inequality (3) is true.
Relation (5) can be a result of agreement among emitters. For example, the equalities , or
, or , where
, where  or, correspondingly,
or, correspondingly,  , are used in [2,3] for the distribution of the monetary resource in problems of collective investment. In geometrical terms the proposed optimal principle (see (4)) implies that desired vector
, are used in [2,3] for the distribution of the monetary resource in problems of collective investment. In geometrical terms the proposed optimal principle (see (4)) implies that desired vector

has the smallest length. Its coordinates are differences in emission densities per capita for groups with adjacent numbers. This approach to the choice of positive parameters  is of great “psychological” significance. The smaller their values, the easier it is to come to the conclusion of the contract if emitters have agreed with the principle of division into groups, which is reflected in (3).
is of great “psychological” significance. The smaller their values, the easier it is to come to the conclusion of the contract if emitters have agreed with the principle of division into groups, which is reflected in (3).
The obtained solution of the mathematical problem under consideration provides a way to define the admissible quantity of emissions for the group with number . In previous notations, the following formula is correct
. In previous notations, the following formula is correct
 (6)
(6)
where  is the solution of Problem B.
is the solution of Problem B.
5.2. Another Variant of the Problem Statement
The conditional rating of every group can be determined based on another criterion, e.g. its living area. In this case the previous notations have the following meaning:  is the living area of the group with number k, where
is the living area of the group with number k, where  is the total living area;
is the total living area;  ,
,  is, respectively, the mean quantity of emissions per area unit of the total living area and for the group with number k, where
is, respectively, the mean quantity of emissions per area unit of the total living area and for the group with number k, where  is the portion of the territory of this group;
is the portion of the territory of this group; ,
, . Coefficients
. Coefficients  are chosen realized by solving the same extremal problem.
are chosen realized by solving the same extremal problem.
5.3. Examples of Problem B Solution
We illustrate a possible way of Problem B solution using two simple examples. This mathematical approach to search of Problem B solution differs from the way of solution in [1-3] (Maergoiz et al., 2010, 2011).
Example 1. Assume in the notations of subsection 4.1 V = 410 million tons,  ,
,  milliard peoples. Suppose that the inequality (3) is the following one:
milliard peoples. Suppose that the inequality (3) is the following one:
 (7)
(7)
and it is taken the equality (5) in the form , where
, where . At first we find the solution
. At first we find the solution  in the more general case provided that
in the more general case provided that
 (8)
(8)
(Problem A solution [1-3]):
 (9)
(9)
where ,
,
 ;
; .
.
Let in the previous notations . Then
. Then  By (9), we have
By (9), we have

It is easy to check that the inequality (7) is fulfilled. Assume . Then
. Then 

 Based on this and (6), we find desired parameters V1 = 90, V2 = 140, V3 = 180 million tons of emissions.
Based on this and (6), we find desired parameters V1 = 90, V2 = 140, V3 = 180 million tons of emissions.
Taking into consideration the another variant of the problem statement (see 4.2) consider the following example.
Example 2. Assume in the notations of subsection 4.1 V = 340 milliard tons,  , S = 150 million km2. Take the inequality (3) in such form
, S = 150 million km2. Take the inequality (3) in such form
 (10)
(10)
and choose the following equality (5) , where
, where  is a number, admissible for existence of Problem A solution (see example 1, inequality (8)).
is a number, admissible for existence of Problem A solution (see example 1, inequality (8)).
In this case, we obtain the following solution of Problem A in the notations of example 1:
 (11)
(11)
where , and, consequently,
, and, consequently,
 (12)
(12)
Suppose in the previous notations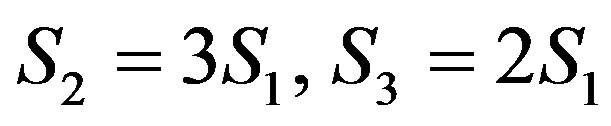 . Then
. Then ,
,  ,
,  ,
, 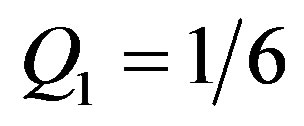 ,
,  ,
,  ,
, . By using formulas (11) and (12), we have
. By using formulas (11) and (12), we have

Hence , and the equality (10) is true. Let
, and the equality (10) is true. Let . In a similar way, we find desired parameters
. In a similar way, we find desired parameters 

 Finally, from (6) we deduce
Finally, from (6) we deduce

 ,
,  milliard tons of emissions.
milliard tons of emissions.
6. Conclusion
The quickest way for solution of global climate changes problem is to find an objective criterion of the distribution of greenhouse gas emissions. A mathematical approach to discovery of this criterion is proposed in the paper.
NOTES