Strong Laws of Large Numbers for Arrays of Rowwise Conditionally Negatively Dependent Random Variables ()
1. Introduction and Preliminaries
Concepts of negative dependence have been useful in developing laws of large numbers (cf: Taylor, Patterson and Bozorgnia [1]). Chung-type laws of large numbers for arrays of independent random variables were developed by Taylor, Patterson and Bozorgnia in [2].
Definition 1.1 Two random variables X and Y are pairwise negatively dependent (ND) if
 (1)
(1)
for all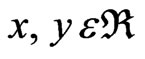 .
.
Let (W, F, P) denote a probability space.
Definition 1.2. The sequence of random variables  is said to be conditionally negatively dependent if there exists a sub s-field z of F such that for each positive integer m
is said to be conditionally negatively dependent if there exists a sub s-field z of F such that for each positive integer m
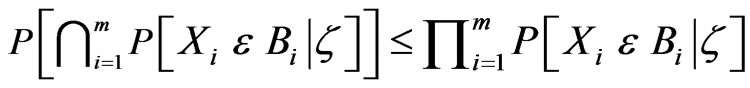 (2)
(2)
where  denotes the conditional probability of the random variable X being in the Boral set
denotes the conditional probability of the random variable X being in the Boral set 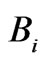 given the sub-s field z. Negatively dependent random variable are conditionally negatively dependent with respect to the trivial s-field
given the sub-s field z. Negatively dependent random variable are conditionally negatively dependent with respect to the trivial s-field .
.
Throughout this paper  will denote rowwise conditionally independent random variables such that
will denote rowwise conditionally independent random variables such that  for all n and k. The major result of this paper shows that
for all n and k. The major result of this paper shows that
 . (3)
. (3)
where complete convergence is defined (Hsu and Robbins [3]) by
 . (4)
. (4)
Here  is a function on a separable Banach space toR. In the next section of this paper, strong laws of large numbers for arrays of rowwise conditionally negatively dependent random variables.
is a function on a separable Banach space toR. In the next section of this paper, strong laws of large numbers for arrays of rowwise conditionally negatively dependent random variables.
2. Strong Law for Random Variables
In this section, several lemmas are used in the proof of the major result. The first lemma will be presented without proof.
Lemma 2.1. Let X and Y be pairwise negatively dependent random variables. Then
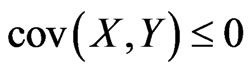
Lemma 2.2. Let X and Y be pairwise negatively dependent random variables. Then
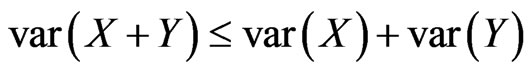
Proof: For X and Y negatively dependent, we have by Lemma 2.1
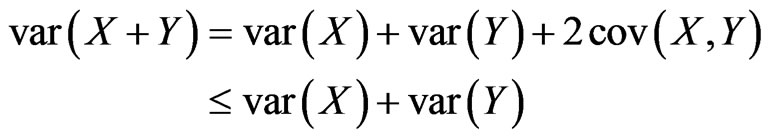
Theorem 2.1 Let 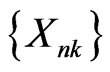 be an array of rowwise conditionally negatively dependent random variables. If
be an array of rowwise conditionally negatively dependent random variables. If
a) (5)
(5)
and for all h > 0
b)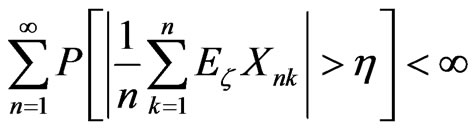 (6)
(6)
where  is the conditional expectation with respect to an appropriate s-field that gives conditional negative dependence. Then
is the conditional expectation with respect to an appropriate s-field that gives conditional negative dependence. Then
 .
.
Proof. Let h > 0 be given. By Markov’ inequality
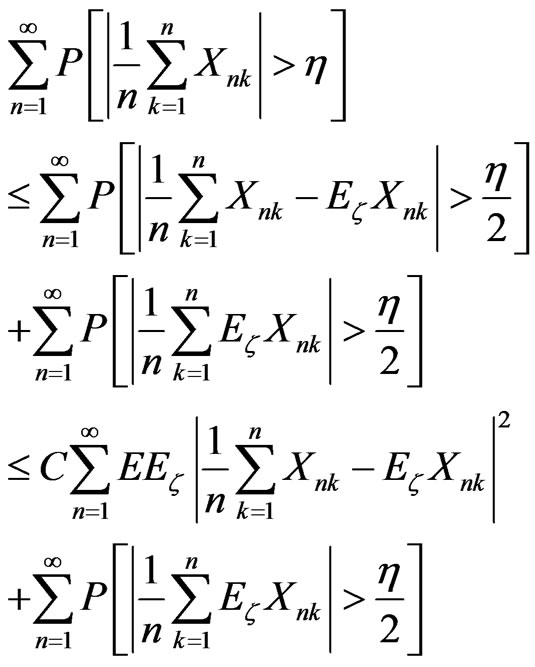 (7)
(7)
By Lemma 2.2, the first term in Equation (7) is bounded by
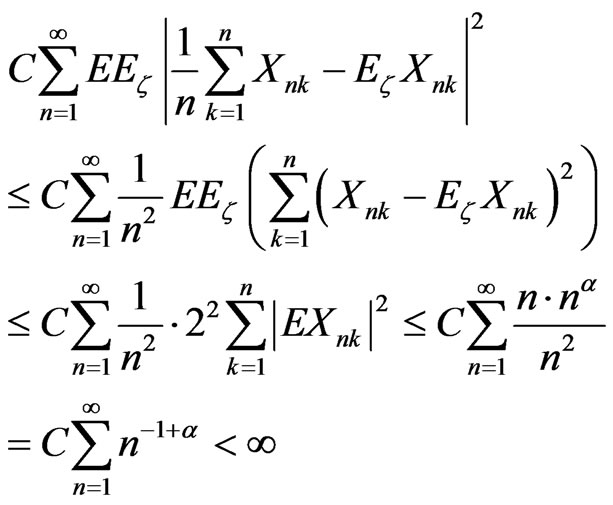 .
.
The second term of Equation (7) is finite by Equation (6). Thus, the result follows.
3. Strong Law for Random Elements in Rm
Theorem 1.2 can be extended to Rm. The next definition is a crucial type p inequality used to define a form of negative dependence (cf. Patterson, Taylor, and Bozorgnia [4]).
Definition 3.1. Random elements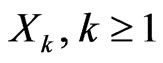 , in a type p Banach space
, in a type p Banach space 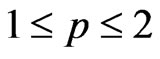 are said to be type p negatively dependent if
are said to be type p negatively dependent if  and if there exist a finite positive constant C such that
and if there exist a finite positive constant C such that
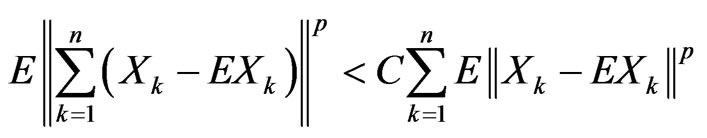 (8)
(8)
for all n ≥ 1.
Coordinatewise (with respect to the standard basis) negative dependence in Rm can yield type 2 negative dependence. To see this for rowwise random elements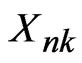 , let
, let 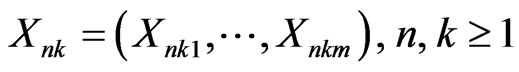 be random elements in Rm such that
be random elements in Rm such that  for 1≤ i ≤ m, n, k ≥ 1. Then
for 1≤ i ≤ m, n, k ≥ 1. Then
 (9)
(9)
Theorem 3.1 Let 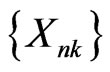 be an array of rowwise conditionally coordinatewise negatively random elements in Rm. If a)
be an array of rowwise conditionally coordinatewise negatively random elements in Rm. If a)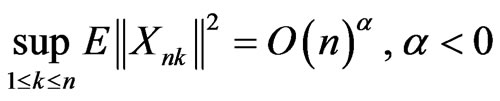 (10)
(10)
and for all h > 0 b)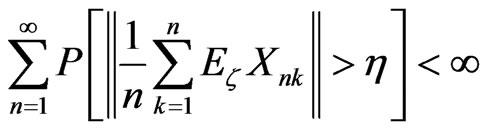 (11)
(11)
where  is the conditional expectation with respect to an appropriate s-field that gives conditional negative dependence, then
is the conditional expectation with respect to an appropriate s-field that gives conditional negative dependence, then

Proof. The proof is similar to that of Theorem 2.1.