Saturated Power Control Scheme for Kalman Filtering via Wireless Sensor Networks ()
1. Introduction
Recently, the rapid evolution of wireless sensor networks, see e.g., [1-4] has made wireless sensors (WSs) cheap and reliable enough to be brought into commercial use. WSs offers several advantages for industrial control systems, such as flexibility, low cost, and fast deployment. Furthermore, WSs and actuators can be placed where wires cannot go, or where power sockets are unavailable. The use of wireless communications for state estimation and closed loop control, however, also brings new challenges in system design.
A drawback of using wireless channels is that they are subject to fading and interference, which frequently leads to packet errors [5-8]. Interestingly, the time-variability of the fading channel can be compensated for by adjusting the power levels [9-13]. Since energy is severely limited in most WS applications, power control design involves trading energy consumption for accuracy [14-18]. Thus, an important challenge is to design suitable power control schemes [19].
Kalman filters are widespread in estimation and control applications, and the effect of random measurement losses on filter stability has received considerable attention in the literature. In particular, Sinopoli et al. [20]
studied a single link estimation setup for linear timeinvariant (LTI) plants where the packet dropout processes are independent and identically distributed (i.i.d.). In this modeling paradigm, it was assumed that the packet dropout probability remains unchanged from one transmission to the next, and all the sensor measurements need to be encoded in a single packet and the sensors should be collocated. The result was extended to deal with the general case of multi-channel Kalman filtering problem [21]. The existence of the critical arrival rate of the observation was proved and both the upper and the lower bound were computed. Plarre and Bullo [22] examines a state estimation architecture with two channels affected by i.i.d. packet dropouts. The case of Kalman filtering with a single link was investigated in Huang and Dey [23-25], where the packet dropouts are described by a time homogeneous two-state Markov chain. Zhang [26] considered a multi-rate distributed estimation problem for wireless sensor networks with packet dropout, the output measurements of the adjacent nodes’ are utilized to generate the state estimation and then fused. In [27], sufficient conditions are established which ensure the convergence of the Kalman filter co-variance matrix. The conditions obtained are used to formulate stabilizing optimal power allocation laws which minimize the total power used by each sensor.
Inspired by the previous work [27], saturated power controllers are designed which provide a time-varying successful probability by inverting the channel gain. We can prove that there exists a critical value such that the expectation of the estimation error covariance is always bounded if the arrival probability of an observation at time is greater than the value. We call the critical value as the admissible packet arrival rate and the computational procedure is presented to design the power controller gain according to the value.
Notation: We write  for the conditional probability of
for the conditional probability of  given
given , and
, and  for the unconditional probability. A random vector
for the unconditional probability. A random vector , which is Gaussian distributed with mean value m and covariance matrix
, which is Gaussian distributed with mean value m and covariance matrix  is denoted by
is denoted by .
.
2. Problem Formulation
Consider an uncontrolled LTI n-dimensional systems:
 (1)
(1)
where the initial system state is Gaussian distributed with mean  and covariance
and covariance . The driving noise process
. The driving noise process  is i.i.d., where each
is i.i.d., where each .
.
To remotely estimate the system state sequence , a network of L sensors is used. Each sensor
, a network of L sensors is used. Each sensor  provides a nosiy measurement signal, say
provides a nosiy measurement signal, say :
:
 (2)
(2)
where  is an i.i.d. process with each
is an i.i.d. process with each 
The L values in (2) are transmitted through the wireless links to the single gateway. The received signals are then used to remotely estimate the state of system (1). In the following scenario, we assume that L = 2 for the sake of convenience, i.e., there are two measurement outputs encoded separately and sent over different wireless channels at each time step:

with .
.
2.1. Channel with Rayleigh Fading
In the present work, we will adopt a block-fading channel gain model, which is a common information theoretic model for fading wireless channels where the channel power gains remain invariant over a block [21]. Furthermore, we assume the single measurement  to be a packet, thus, the block length equals the packet transmission time. The associated channel gain processes are denoted by
to be a packet, thus, the block length equals the packet transmission time. The associated channel gain processes are denoted by  (“
(“ ”), which are exponentially distributed with cdf
”), which are exponentially distributed with cdf
 (3)
(3)
where, .
.
Suppose that the binary phase shift keying transmission over the i.i.d. block fading additive white Gaussian noise channels is used [26]. Each sensor measurement consists of a packet containing b bits. Since the bit errors are independent within a packet, the success probabilities can be written as, see [6],
 (4)
(4)
After approximate calculation, we have the following theorem.
Theorem 1
 (5)
(5)
Proof: For a random variable , its cdf can be represented by
, its cdf can be represented by

It is easy to see

The second equality is obtained if we approximate square with round, i.e.,

and obtain

which yields (5). This ends the proof of Theorem 1.
Since the l links between sensors and gateway are wireless, transmission errors are likely to occur. Faulty packets will be discarded when estimating the system state. We will model transmission effects by introducing the l binary stochastic arrival processes , where:
, where:

The success probabilities of  are determined by the propagation environment and transmission power. In the present work, the saturated power controller is used
are determined by the propagation environment and transmission power. In the present work, the saturated power controller is used
 (6)
(6)
where  is the peak power level, and
is the peak power level, and  is the power controller gain for the
is the power controller gain for the  channel. Moreover,
channel. Moreover,
 (7)
(7)
For further reference, we also define the overall arrival process of all l links, say  via
via
 (8)
(8)
We will assume that the data transmission incorporates error detection coding. Hence, the gateway knows the packets received from the sensors contain errors or not. Thus, at any time k, the past and present realizations of the overall transmission process are available at the gateway. For state estimation purposes, the system amounts to sampling (1)-(2) only at the successful transmission instants of each sensor link. Indeed, the conditional probability distribution of the system state at any time k, given the correctly received sensor measurements up to time k, is Gaussian.
Let , we define
, we define

The time update of the Kalman filter is independent of the observation process and thus stays the same as in the classical Kalman filter:
 (9)
(9)
The measurement update is now stochastic since the received measurements depend on the random variables  and
and .
.
Let , a general form of the error covariance matrix is given by
, a general form of the error covariance matrix is given by
 (10)
(10)
In the next section, we will focus on the statistical properties of the error estimation covariance .
.
3. Convergence Conditions
First, we define the modified algevraic Riccati equation for the Kalman filter with random packet dropout as follows,
 (11)
(11)
Some useful properties of the function  are presented and the proof can be found in [21].
are presented and the proof can be found in [21].
Lemma 1 [21]  is concanve and nondecreasing function in X.
is concanve and nondecreasing function in X.
Lemma 2 [21] For fixed ,
,  is decreasing in
is decreasing in , vice versa for
, vice versa for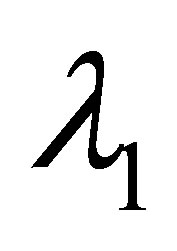 .
.
Lemma 3 [21] .
.
Lemma 4 [21] Suppose  matrices
matrices  and
and  such that
such that , then a)
, then a) , the iteration
, the iteration  converges and
converges and
 (12)
(12)
independent of initial condition P0.
b)  is the unique positive semidefinite solution of
is the unique positive semidefinite solution of 
Lemma 5 [21] Assuming  is controllable and
is controllable and  observable. Fix
observable. Fix . If
. If  is unstable for
is unstable for , whereas stable for
, whereas stable for , then
, then  such that
such that
 (13)
(13)
Furthermore, there exists a positive semidefinite matrix  as a function of the initial condition
as a function of the initial condition , such that
, such that
 (14)
(14)
The vice visa for fixed .
.
The following theorem gives the power controller gain region for the above critical value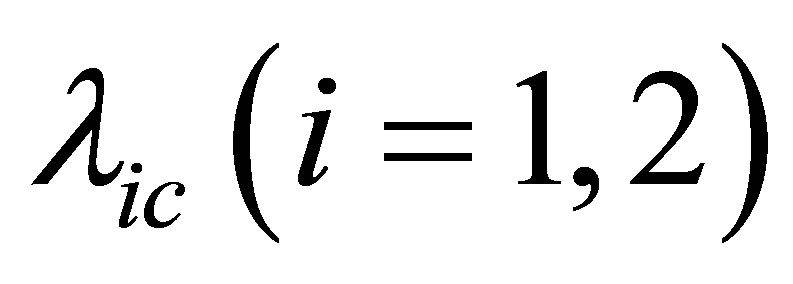 .
.
Theorem 2 Assuming  is controllable and
is controllable and  observable. Fix
observable. Fix . If
. If  is unstable which meets (13), then the corresponding power controller gain satisfies
is unstable which meets (13), then the corresponding power controller gain satisfies
 (15)
(15)
for  mentioned above.
mentioned above.
Proof: The proof is established based on Theorem 1 and Lemma 5. When , Equation (5) has an equivalent form
, Equation (5) has an equivalent form

when , we can easily obtain
, we can easily obtain

when , we obtain
, we obtain  from (6), which yields
from (6), which yields

this ends the proof of Theorem 2.
The distributed protocol mentioned above is sketched below:
Procedure:
Step 1) For given , we use bisection method to find
, we use bisection method to find . For
. For , search the
, search the  interval to find some
interval to find some , such that
, such that  .
.
Step 2) For the same 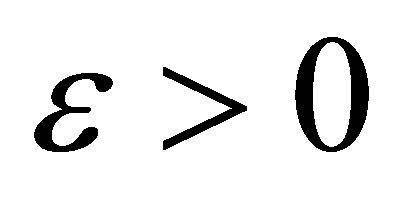 and
and , search the
, search the  interval to find some
interval to find some , such that
, such that . Use this method, we can find the greatest lower bound of the critical value
. Use this method, we can find the greatest lower bound of the critical value .
.
Step 3) Design the power controller gain according to the above admissive upper bound obtained in Step 2).
Remark 1 It follows from the reasoning above that one can improve the transmission reliability and the state estimation accuracy for a given wireless propagation environment simply by increasing the power controller gain used by the transmitter. However, it is of fundamental importance to save energy in wireless sensor networks. There is the tradeoff between the stability of Kalman filter and a energy resource.
4. Conclusions
An energy efficient power control scheme for state estimation via wireless sensor networks operating over fading channels was presented. The time variability of the fading channels frequently leads to transmission errors with subsequent random packet drops. State estimation in the face of intermittent observations was then performed by a time-varying Kalman filter. In our scheme, the transmission power of the radio amplifier of each of the wireless sensors was controlled by the gateway. For that purpose, we proposed a saturated power controller.
The results in this paper can also be generalized to the case where the observation data is contained in more than two packets. In the generalization, the Kalman filter updating upon one or more packet losses can be computed in the same manner since we can always divide the observation into two parts: the received and the lost. The statistical properties of the error covariance matrix iteration stay the same with appropriate extensions. In our future work, we would like to study the convergence properties of the Kalman filtering problem.
NOTES