New Approach of Geomechanical Properties by Scale Effect and Fractal Analysis in the Kedougou-Kenieba Inlier (Senegal-West Africa) ()
1. Introduction
The West African Craton has been the object of many geological studies which concluded substantial knowledge of the Precambrian in Senegal. This research is mainly focused on the domain of the basic principle of geology and mines. In this paper, we are interested in the geometrical aspects of rocks. Geometrical aspects are represented by fractal geometry and scale effect, which permit to analyze the appearance in term of microscopic and macroscopic dimension.
Fracture systems in the south eastern Senegal are discontinuous structures or discrete breaks within a rock mass that are developed by response to stress. Fractures include faults, joints, and filled structures such as veins. These figures appear in the area on a wide range of scales from microns to several hundreds of meters. In recent years, it has been suggested that various technics of fractals may usefully be applied to the study of spatial distribution of fractures, because of similarities between small and large-scale fracture arrays, which have been found over many orders of magnitude [1]. This work deals with the consequence of the structuration of the rock mass in their geometry. The fractal geometry and scale effect allow estimating the occurrence of the fracturation and other parameters to the studies of discontinuities. For these estimations, we introduce a more complex aspect using the filling materials and define the “scale coefficient”.
2. Geological Framework
Three main directions of discontinuities characterize the Proterozoic rock masses. In the Birimian domain, the discontinuities show a very large motion due to the complexity of the geological history. The structures correspond mainly to the boundary of the rock formations. In these domains, discontinuities show some shear that are dextral NE-SW or senestral NW-SE [2]. The fractures are sometimes conjugated. In the Kédougou-Kéniéba Inlier (KKI), [3-5] bring out three main Eburnean tectonic phases: 1) A D1 phase, fairly high crustal level tectonic activity with a tendency toward thrusting; 2) A D2 phase related to the major senestral shear zones and the emplacement of granitic intrusions [6-7]. This second phase is responsible of large sub meridian senestral shear corridors, where the most important are: The Main Transcurent Shear Zone (MTZ), separating Mako and Dialé Supergroups [3-8] and the Senegal-Mali fault (SMF), along the western Falémé bank [9] (Figure 1); 3) A D3 Eburnean tectonic phase has been also characterized by [5] in the Birimian formations of the KédougouKéniéba Inlier (KKI).
Some authors show that the Birimian of Senegal show relative amount of faults D2 and D1. D2 is identified in all the Birimian (Mako super-group with volcanic rocks and Dialé-Daléma supergroup with sedimentary ones associate to volcanic ones) and D1 is only presents in the DialeDalema [4,10-12]. While these deformations are considered to be represented in the scale of the West African domain, D1 is absent in some sector. In the new denomination by [2], D1 and D2 are respectively called Dt1 and Dt2. They belong to a continuum transcurent tectonic system Dt. So, this transcurent tectonic occurs in two stapes (Dt1 and Dt2). This consideration is different of the first one, which defended that D1 is tangential and D2 is transcurent [4]. The hypothesis of a continuum transcurent tectonic defined by [2] is also supported by the fold produced when schistosity occurred and which would be folded again. The two stages of folds have the same axial surface oriented (N (20 to 40) - (10 to 30) NW).
Studies done in the sector of Mako on the latitude of Mako [12] show that this domain is crossed by more important framework of discontinuities as those explained by [2-4]. This framework of discontinuities is caused by the described phenomena, the cracks due to the crystallization of the magma and at least the repercussion of the Hercynian orogenesis. Tectonic fractures were mapped and measured in the field area of Mako and Ségou. The sedimentary rocks show less anisotropy represented essentially by cracks and rarely by faults. They correspond to sandstones mainly associate to pelites rocks [13].
In the Ségou-Madina kouta basin, the domain of Segou is characterized by fracturations, which appear like cracks. These cracks show three directions representing three families of discontinuities NE, ENE and ESE associated to erratic joints.
3. Fractal Theory
The fractal term is used to describe a natural geometry where studied objects are recurrent, fragmentary and
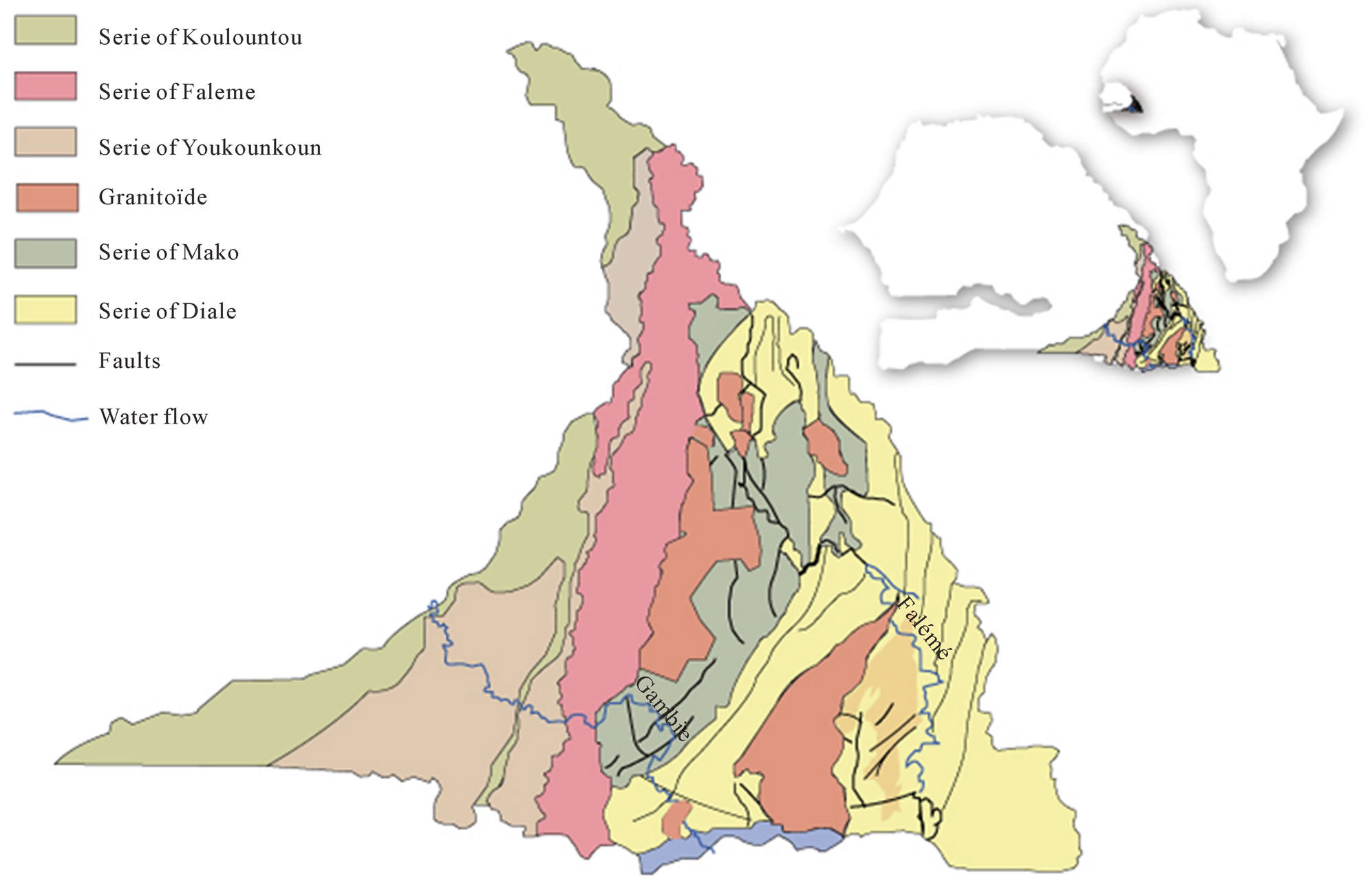
Figure 1. Structural map of the Kédougou-Kéniéba inlier [11 modified by 2 modified].
elements are seen in all scale [14,15]. Mathematicians define fractals using three equations [16]:
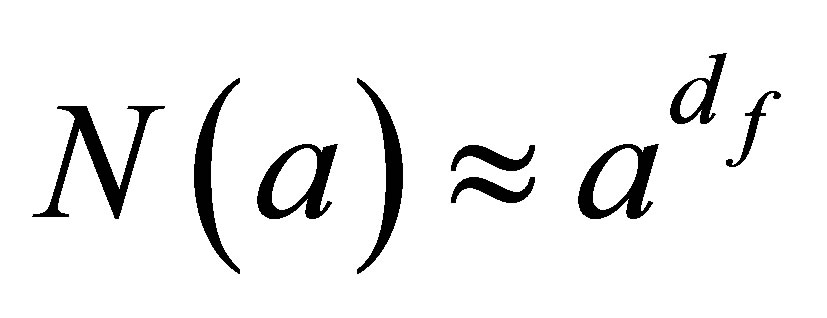 (1)
(1)
N is the number of portions resulting to iteration, a the size of a portion and d the fractal dimension.
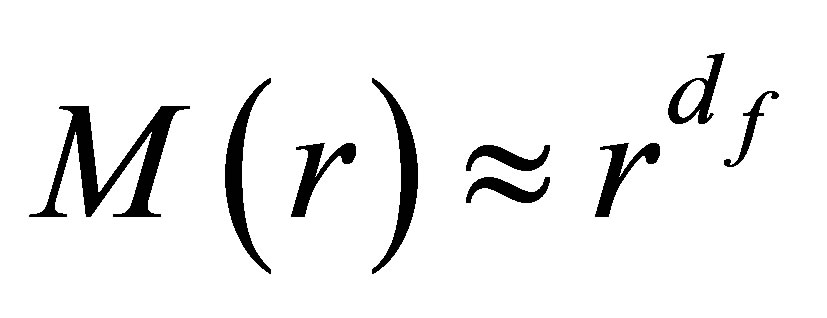 (2)
(2)
M (r) is the weight of a portion and r is its linear extension.
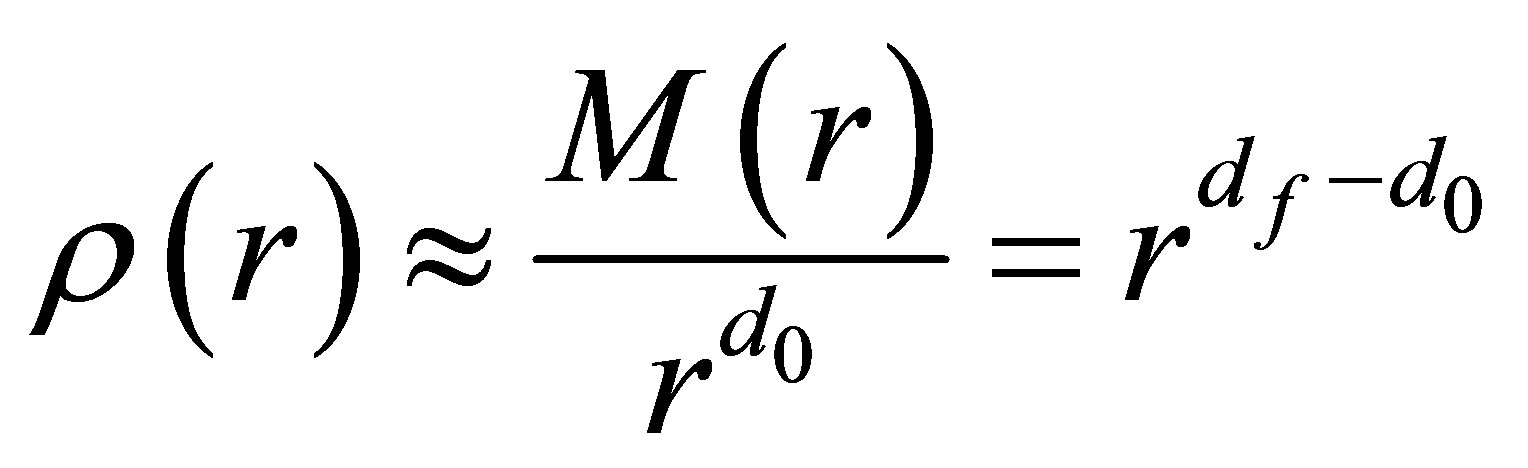 (3)
(3)
ρ(r) is the density.
As Euclidian geometry, fractal geometry is also characterized by a dimension called fractal dimension df. The fractal dimension is fractionary and in difference of Euclidian dimension it is no characteristic of an object. Its value varies between 1 and 3 (1 ˂ df ˂ 3) and different to 2. It is a dimension deduced of the number of portions N(s) after iteration and the length (s) of one portion using the equation
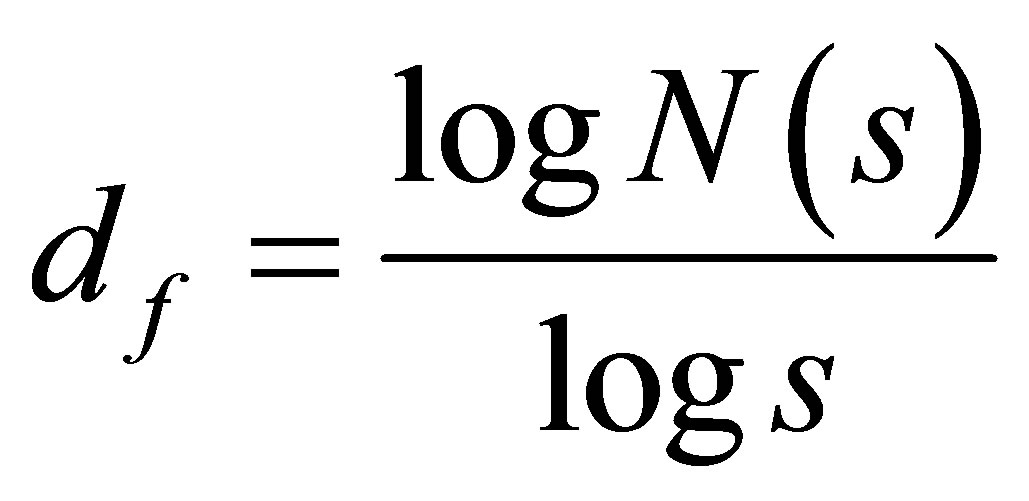 (4)
(4)
In Earth Sciences, the fractal analysis can be used to quantify many elements of discontinuities. It’s the case of spacing, aperture, asperities and length of discontinuities or any other parameter, which allows describing the geometry of discontinuities [17,18]. For easier use, the fractal geometry is described by using process of iteration as the Sierpinsky, the flocon of Koch or the Cantor dust. It is very difficult to determine the fractal dimension by using the definition of fractals. So, in many case, it is done by graphical representation. This graphical resolution consists of plotting, the function log N(s) versus log(s). The obtained curve is linear and it slope corresponds to the fractal dimension. In Earth Sciences and fracture characterizations, the box-counting method is the most used method describing fractal geometry. These geological elements are non-euclidian shapes. The boxcounting method consists of dividing the defined domain in box and analyzing the box cross by discontinuities [18]. Fractal analysis is critical issue due to the complexity of it use. Multifractal theory is developed to take account this complexity which characterizes multiple elements.
4. Theory of Scale Effect of the Rocks
Scale effect is studied by some authors in the literatures [19-22]. Some of them subdivided the scale effect into two components [19] represented by the shape scale which take account the variation of the ratio D/L and the size scale in which this ratio is constant and the size of the specimen growth. For that, values obtained in tests show that shape scale have effect in results of studies but no effect for size effect. About [20], the scale effect is more remarkable for brittle rocks than ductile rocks. The scale effect define by [20] corresponds of shape scale define by [19]. Samples with artificial fractures were also tested to characterize the scale effect on the specimen’s behavior [21]. These authors generated artificial discontinuities on specimens of rocks. Two types of discontinuities are represented. Ones are no embedded and others are embedded. They show that a large framework of fracture on specimen can caused a scale effect while it is considered to be homogeneous. The scale effect is also a characteristic of the in situ rock masses. It influence scale effect in both size and time [23]. For in situ behavior, these authors show that joint which are present in rocks causes scale effect. These joints are characterized by their frequencies; connectivities and spacing caused by rock burst in deep. Another parameter which can be characterized by scale effect in geology and rock engineering is the permeability [24]. The scale effect depends largely on the heterogeneity and the connectivity of discontinuities. Sometimes, discontinuities are no connected. From these authors, there are no correlated parameters characterizing the conductivity of discontinuities on variable directions for the same on the field. So the scale effect is largely discussed in the literature and some functions are put on to model this parameter. So, from laboratory test to field parameters, Hoek-Brown criterion and Zhang and Einstein function can be used. The first permits to define the uniaxial compressive strength and the second the Young moduli. The Zhang and Einstein [25] is defined as:
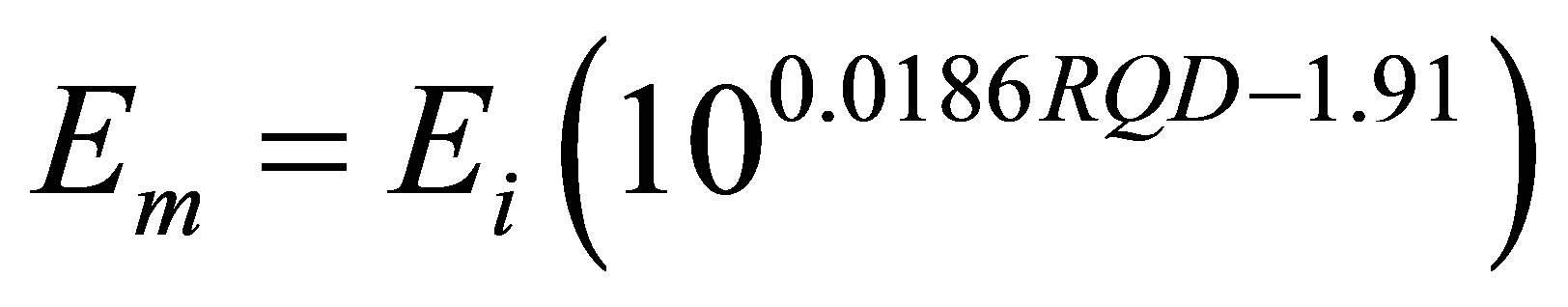 (5)
(5)
Scale effect appears also in some results, which characterize the roughness of joint. That’s why from laboratory parameters to field ones, it is necessary to adapt values. This is valid also for Joint Compressive Strength (JCS). These last elements are defined by taking about scale effect by:
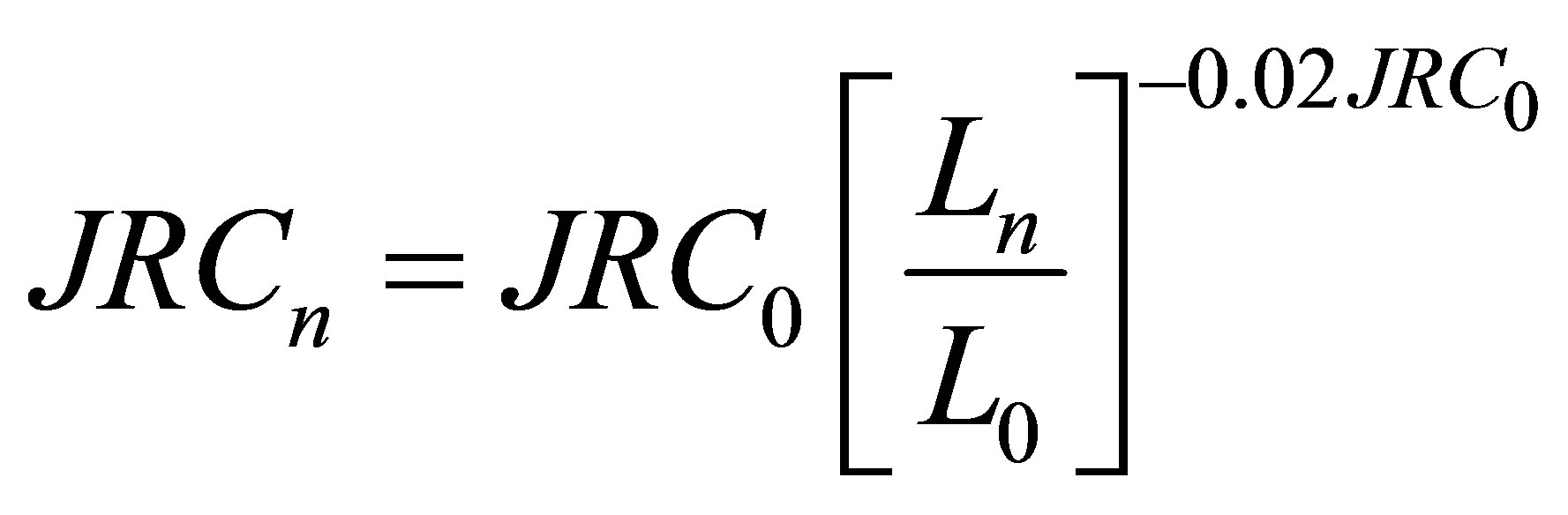 (6)
(6)
The consequence of scale effect is also noted on the result of uniaxial compressive strength. For this, uniaxial compressive strength of a sample is given by taking about the diameter of the study sample and the typical diameter of 50 mm by the function
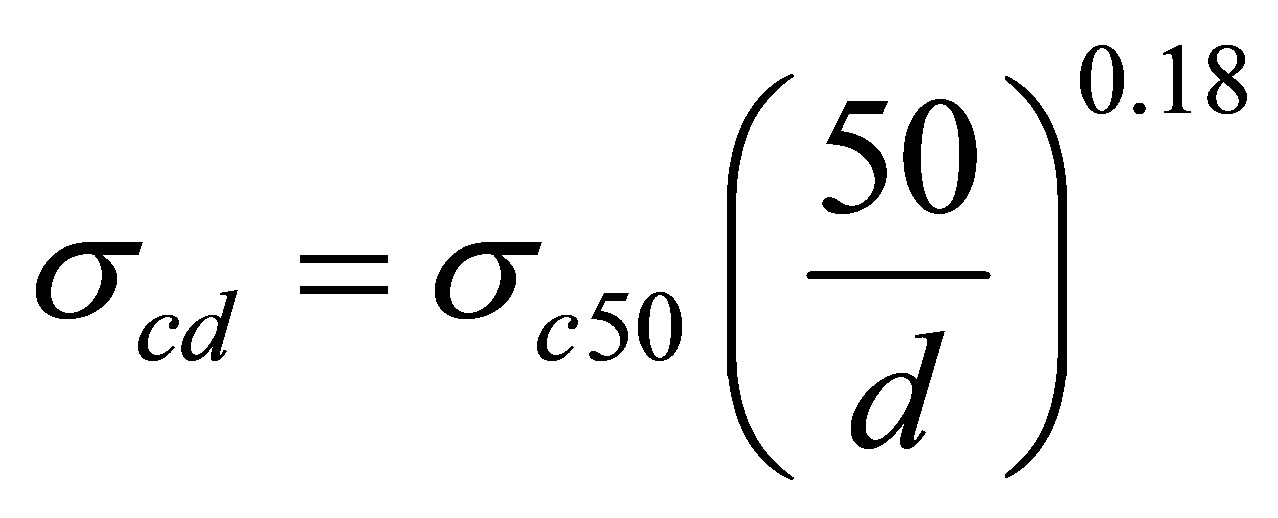 (7)
(7)
In all cases, scale effect is traduced by variations of mechanical parameters when the dimensions of the samples vary. In this paper, it is observed when pass from values of laboratory test to values of field. It depends on the discontinuities of the rocks, type of filling materials. When pass from intact rock to rock with multiple fractures, some of which are filled, these values of mechanical parameters fall down.
5. Structural Analysis of Discontinuities on Studied Rocks
The structural studies carried on the domain of Mako show a very important number of discontinuity families. In this domain, the igneous outcrop rocks (basalt) show also a very important number of fractures, which are represented in the stereogram. This disposition reflects the presence of folds (Figures 2-4). At the west side of Sékoto, the poles of fractures are organized along little circles. So, in this area, the folds are conic (Figure 2). These conic folds show some axes oriented north south.
In the south-west of Bafoundou, the poles of fractures have an organization along a great circle. This kind of organization is characteristic of cylindrical folds (Figure 3). The pole of the great circle meaning cylindrical fold is located in the east side mining that the axe of these folds is east.
This projection (Figure 4) shows a complex appearance. There are poles disposed along a great circle characterizing cylindrical fold and others along little circle traducing conic folds. Axes of cylindrical folds are oriented south-east while ones of conic folds are oriented
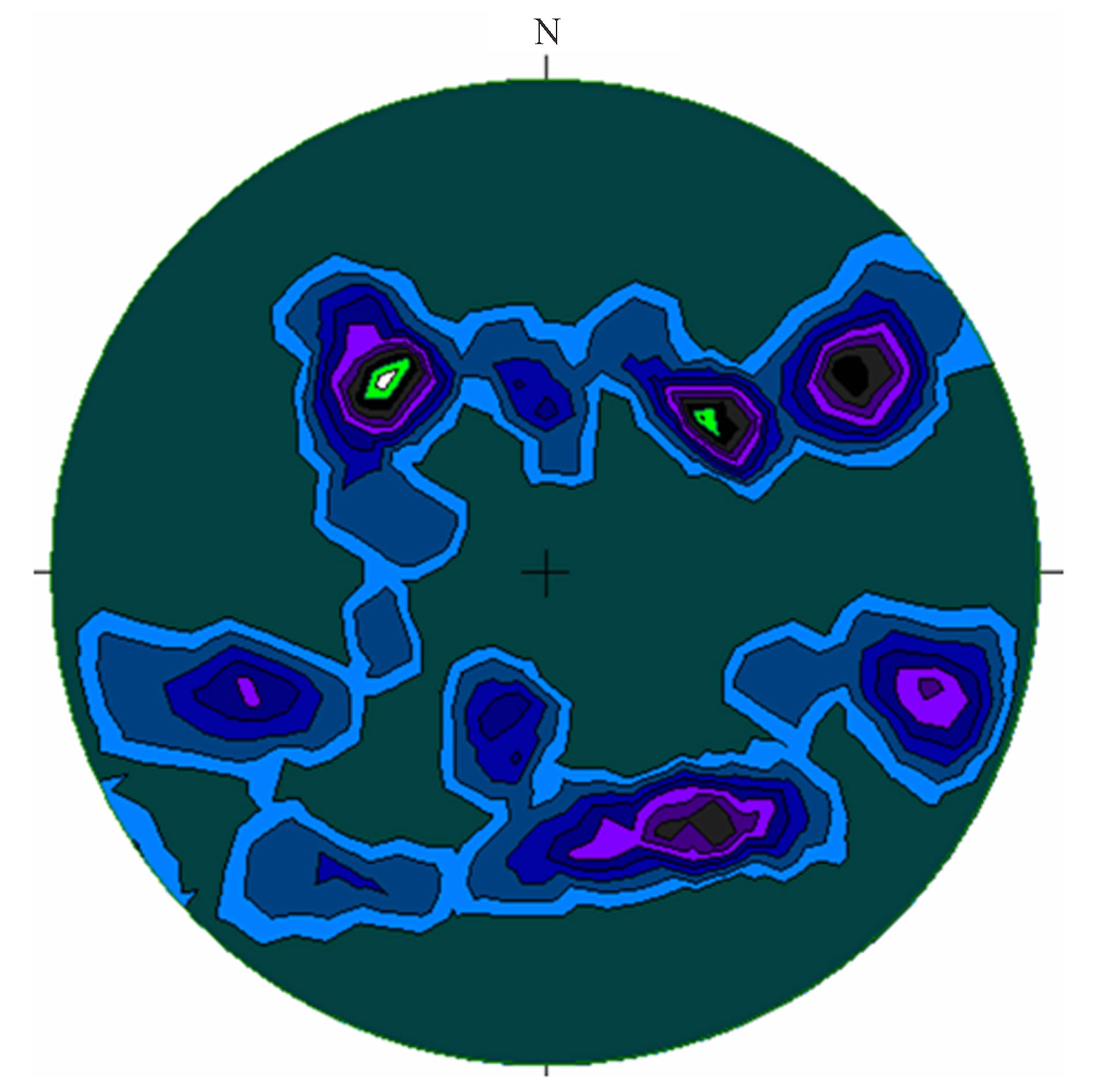
Figure 2. Contoured poles of fractures in the basalts (lower hemisphere equal angle projections): conic folds in the Mako area.
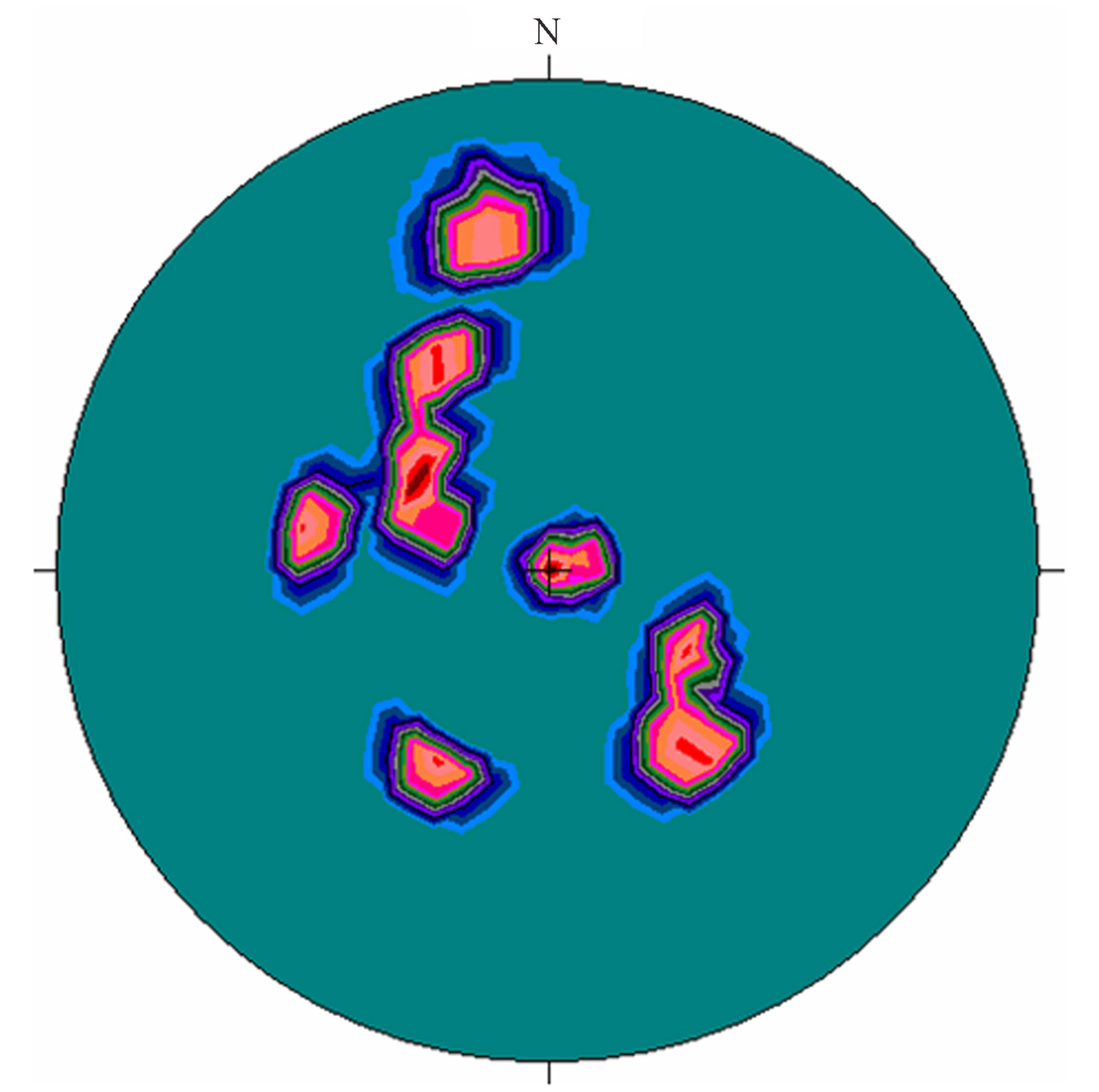
Figure 3. Contoured poles of fractures in the basalts (lower hemisphere equal angle projections): cylindrical folds southwest of Bafoundou.
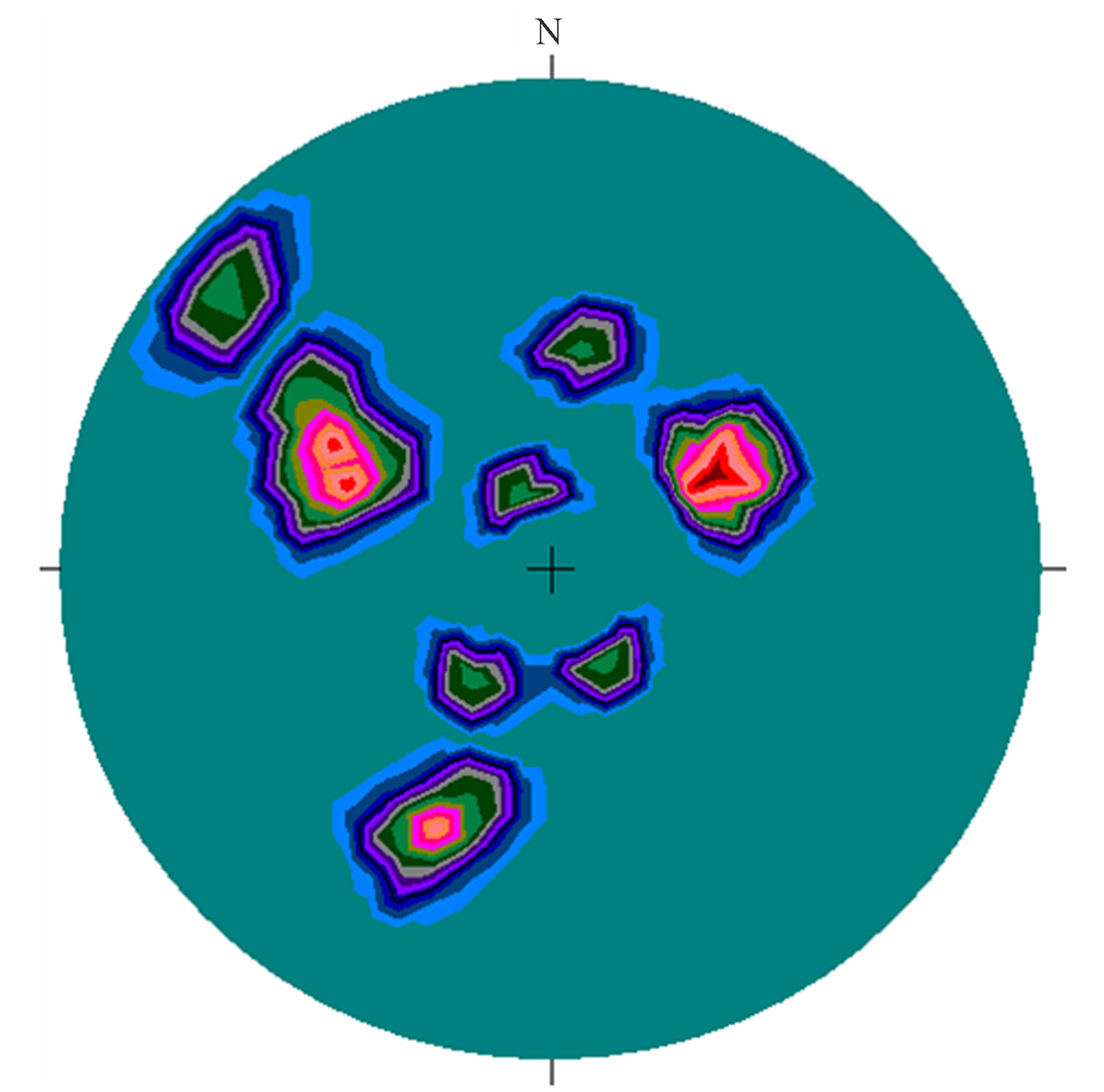
Figure 4. Contoured poles of fractures in the basalts (lower hemisphere equal angle projections): superposed cylindrical and conic fold.
north-south.
Associated to a dome-basin system, they traduce a few different generations of folds that are or not same nature (Figures 2-4). This is due to the complex history of the Mako area in one part traduced by the three eburnean tectonic phases and in another part by the repercussion of Panafrican and Hercynian orogenesis.
Oldest sedimentary rocks of Senegal constitute the domain of Southern east Senegal in the Segou-Madina kouta basin. Those rocks show a simple fracturation represented by cracks and rarely faults which are often parallel to cracks (Figure 5).
On the stereogram, the fracturation of Segou doesn’t show a particular disposition. They are grouped into three families (NE, ENE and ESE) while slight variation of fracturation can be seen. These families of discontinuities are associated with erratic joints accidentally present on the field (Figure 5).
6. Geometric and Spatial Studies
Geometric parameters that caused fracturation and their iteration in the rock are fractal geometry and scale effect. Fractal geometry and scale effect depend on each other because both of them depend on stage and scale of the studies.
6.1. Scale Effect
Studies are conducted from laboratory to field. From one to another scale, rocks show important number of joint. This is a consequence of the scale effect. The increase of the number of discontinuities is due to the fact that in rocks microdiscontinuities are associated to microdiscontinuities. When the sizes of the samples increase, the number of macrodiscontinuities present on the rock increases. The increasing of the number of discontinuities in the specimens affects the mechanical parameters. So, the smallest volume with all directions of discontinuities is called EVR (Elementary Representative Volume). If we have a volume of material equivalent or greater than
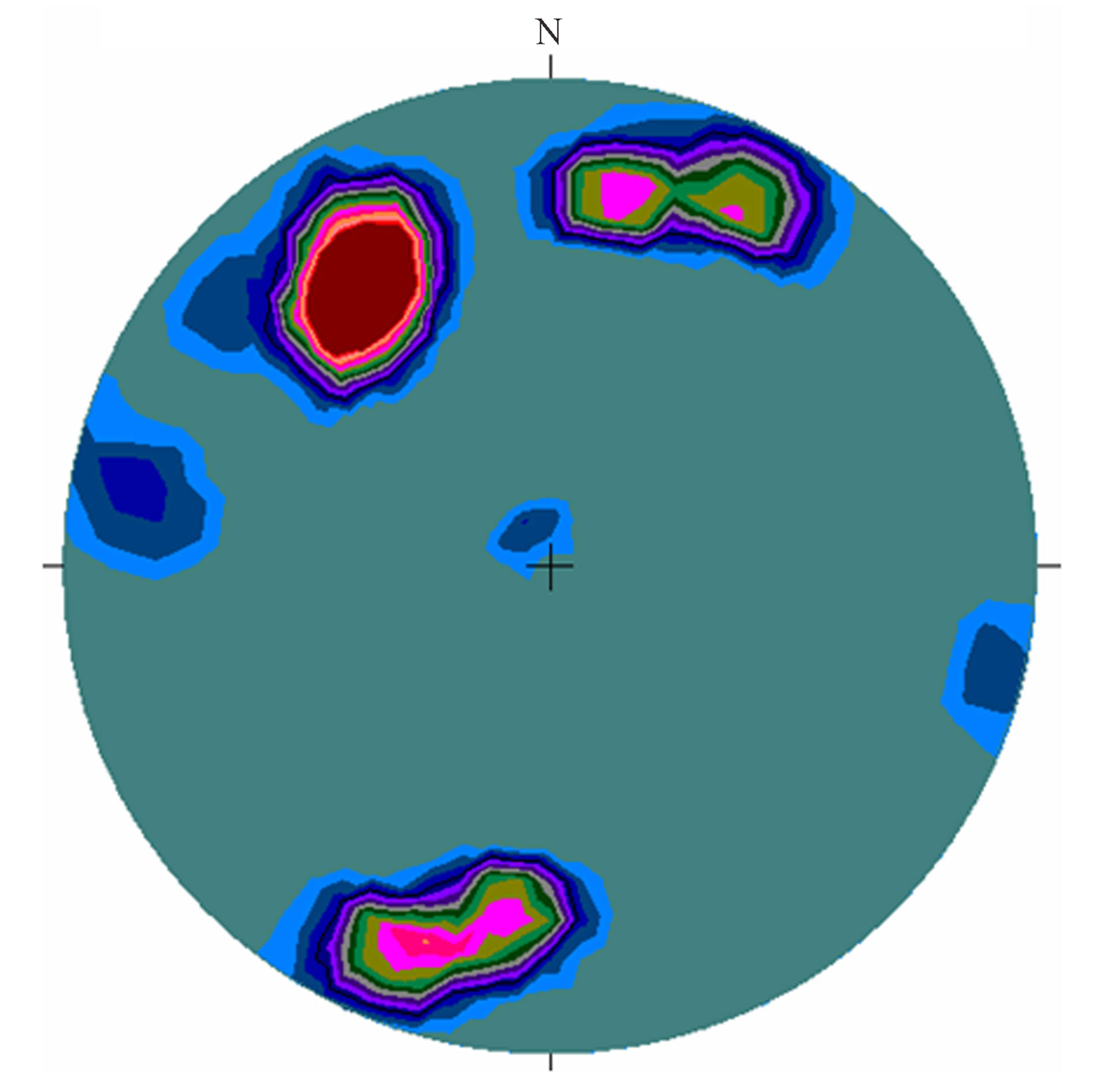
Figure 5. Contoured poles of fractures in the sandstone of Ségou area lower hemisphere equal angle projections.
this volume, mechanical parameters depending on the anisotropy don’t change. They become stable around one value. This phenomenon appears very well in results of studies of all rocks, sedimentary or igneous. It can be remarked by lowest values of uniaxial compressive strength and Young moduli for rock masses than for laboratory samples. But the scale effect is more sensible for basalts than for sandstones (Figures 6 to 8). Structural studies at Mako (domain of basaltic rocks) and Segou (domain of sandstones rocks) show that the network of discontinuities is most complex for basalts. In fact, those sedimentary rocks of Segou are not the area of intensive tectonic history. Discontinuities are represented essentially by cracks. But basalts are affected by D1 and D2 phases of deformation and the Hercynian orogenesis impact. A large number of directions of discontinuities are present. Also, some of these discontinuities are filled with crystallization. Filling minerals are very different.
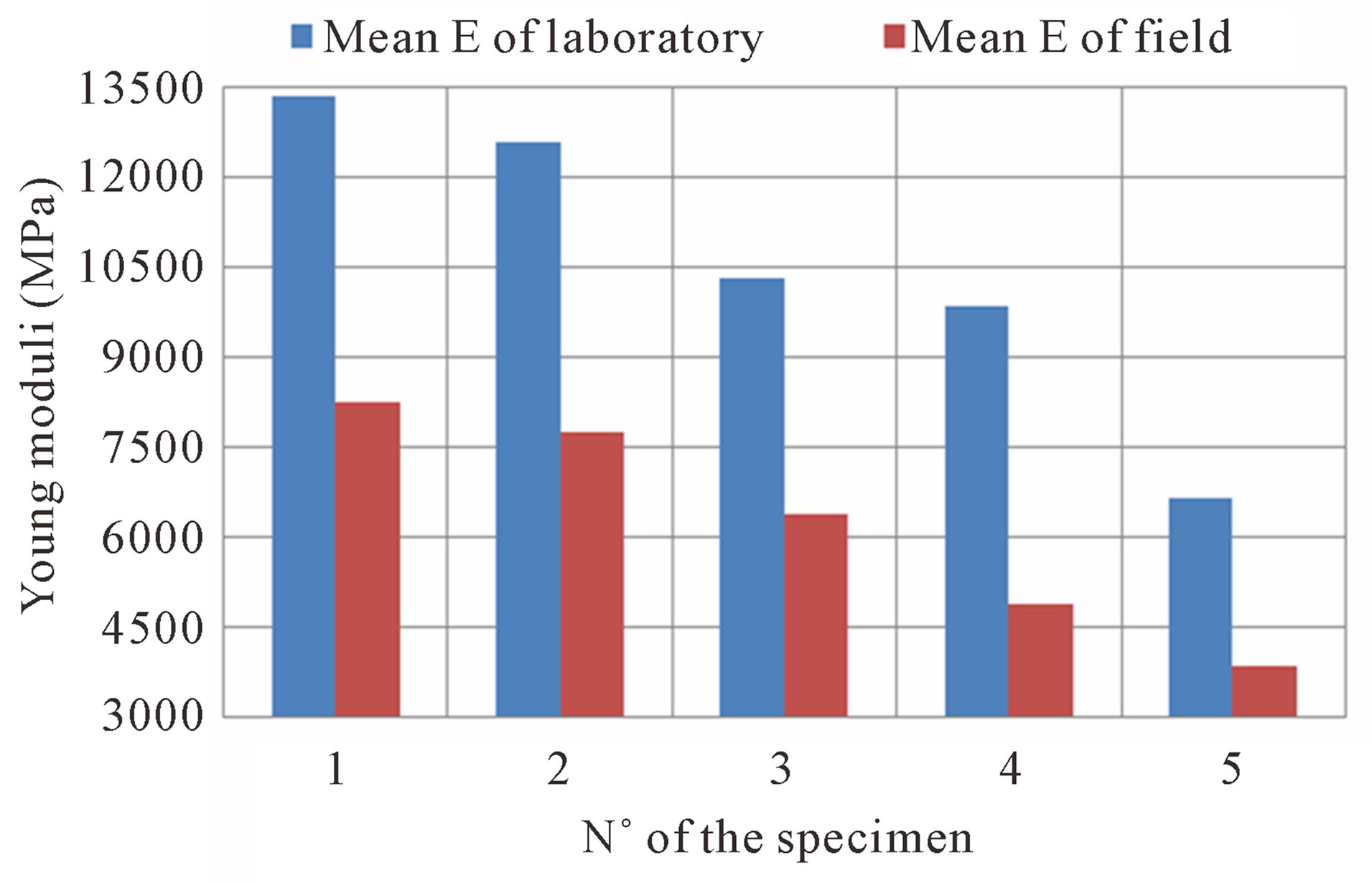
Figure 6. Graphical representation of Young moduli for different kind of basalts in laboratory samples and field ones (1: healthy basalts, 2: basalts with unfilled fractures, 3: basalts with tension cracks filled with quartz, 4: basalts with multiple fractures, 5: basalts with fractures filled with calcite, chlorite, epidote).
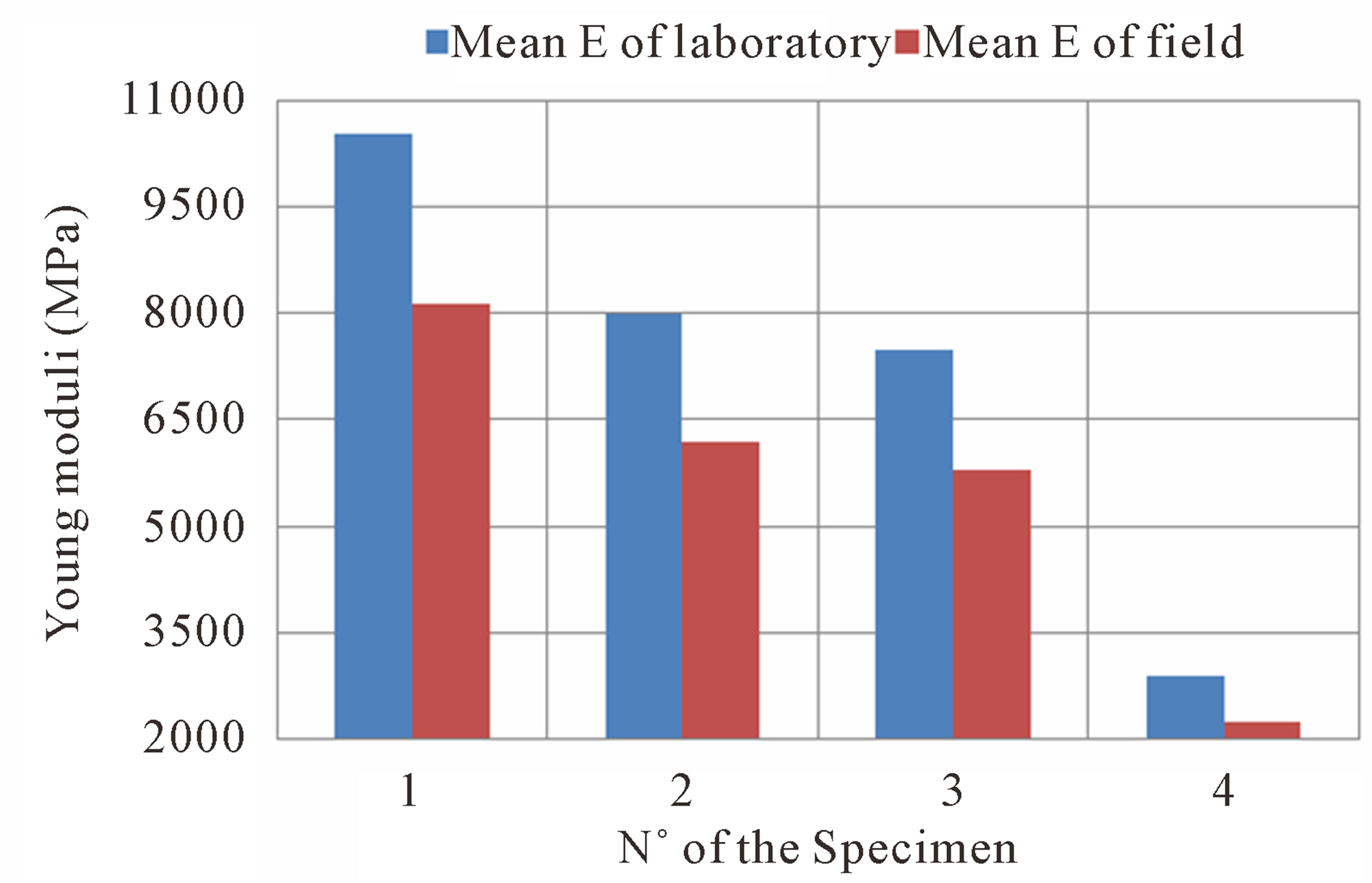
Figure 7. Graphical representation of Young moduli for different kinds of specimens of sandstones (1: white sandstones; 2: red sandstones; 3: purple sandstones; 4: sandstones with intercalation of pelites).
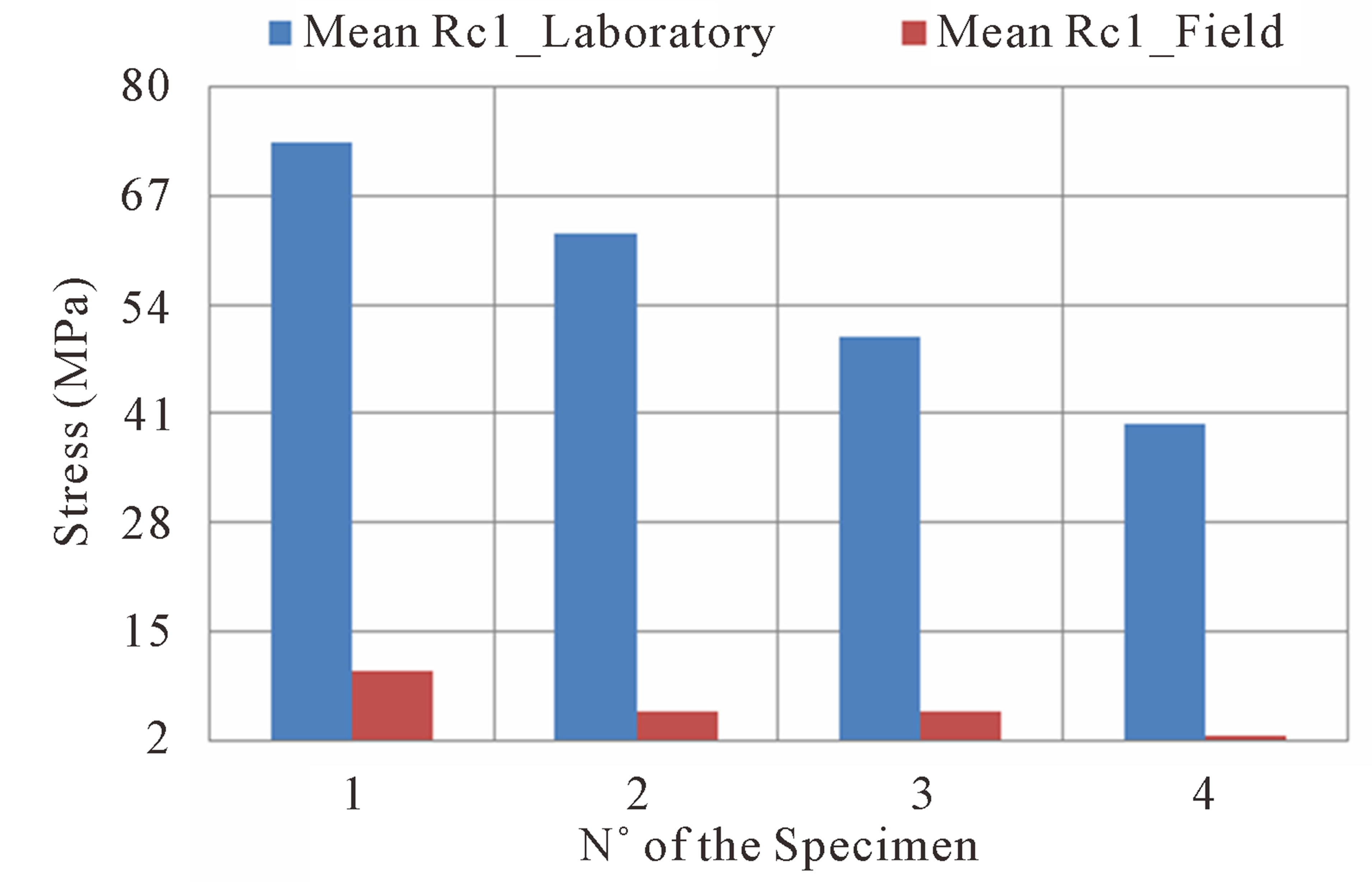
Figure 8. Graphical representation of uni-axial compression stress for different kinds of specimens of sandstones (1: white sandstones; 2: red sandstones; 3: purple sandstones; 4: sandstones with intercalation of pelites).
Some, which are hard, and the others are soft. These facts show that scale effect depends on the fracturation of the rock and the filling minerals of discontinuities.
For basalts (Figure 6), scale effect is very characteristic by the number of family of discontinuities and also the number of filling minerals and their natures. In fact, with these elements, Young moduli of the basalts in laboratory and in the outcrops vary remarkably. This variation is caused by the variability of the product of filling which can be very complex. So, it is very difficult to have a complete element of volume, which can represent the ERV. So, this kind of materials is characterized by a very heterogeneous nature and also, the heterogeneity can vary exceptionally from a locality to another.
In these studies, we introduce a parameter called scale coefficient (ech). This coefficient is obtained by the function:
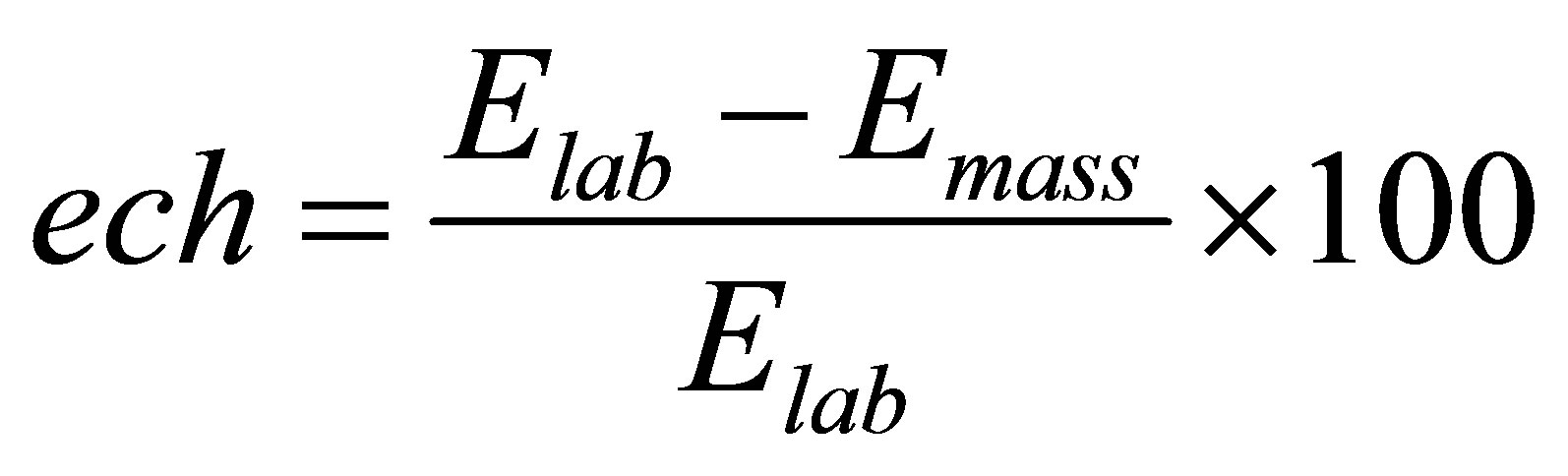 (8)
(8)
Elab is the Young modulus for laboratory sample; Emass is Young modulus of rock mass.
Basalts show large interval of variation of the scale coefficient (between 38% and 50.4%). that is caused by the complexity of the structuration of the samples (Table 1).
Healthy basalts, unfilled fractures basalts and basalts with tension cracks filled with quartz show same values of scale coefficients (38% to 38.3%). That is due to the fact that these cases correspond to a low complexity of structuration.
For basalts with fractures filled with calcite, chlorite and epidote, the scale coefficient increase (42.4%) because of an increase of the level of complexity. The complexity is a consequence of the duality of the material of filling. While calcite is hard, epidote and chlorite are soft.
For basalts with multiple fractures, increasing of the scale coefficient (ech) is most important (50.4%). This is due to a very important level of complexity. The material shows many directions of fractures and some of them are filled with soft materials, others by hard materials and the last ones are unfilled.
Therefore, the dimension of the ERV increases with an increasing of the scale coefficient, which denote of the increasing of the level of complexity of the rock.
Sandstones show also characteristics of scale effect. From laboratory to field values, the Young moduli decrease (Figure 7). This evolution is quite slight because of a low to medium level of complexity. In a structural part of view, the sandstones are crossed by cracks and there are no filling materials which can increase the complexity of the rock mass. Specimens present relatively the same kind of behaviors.
If we consider the scale coefficients (ech) for sandstones, their values are low and vary around 22% for all samples (Table 2). This is due to the fact that the number of discontinuities taking part to the behavior of this rock mass is limited to three and there are no filling materials which reinforce the complexity of the sandstones. While variation is exceptionally low, they are in disfavor of the sandstones with intercalation of pelites.
The scale effect affects also the uniaxial compressive strength (Figure 8). For sandstones, the action of scale effect is most remarkable on uniaxial compressive strength than on Young moduli. Another coefficient that’s method of calculation is similar to the ech and called compression scale coefficient ech’ can be defined using the uniaxial compressive strength for sandstones. This variable is calculated using the following function which whom Rlab is the uniaxial compressive strength (UCS) of laboratory; Rfield is the UCS of the outcrop.
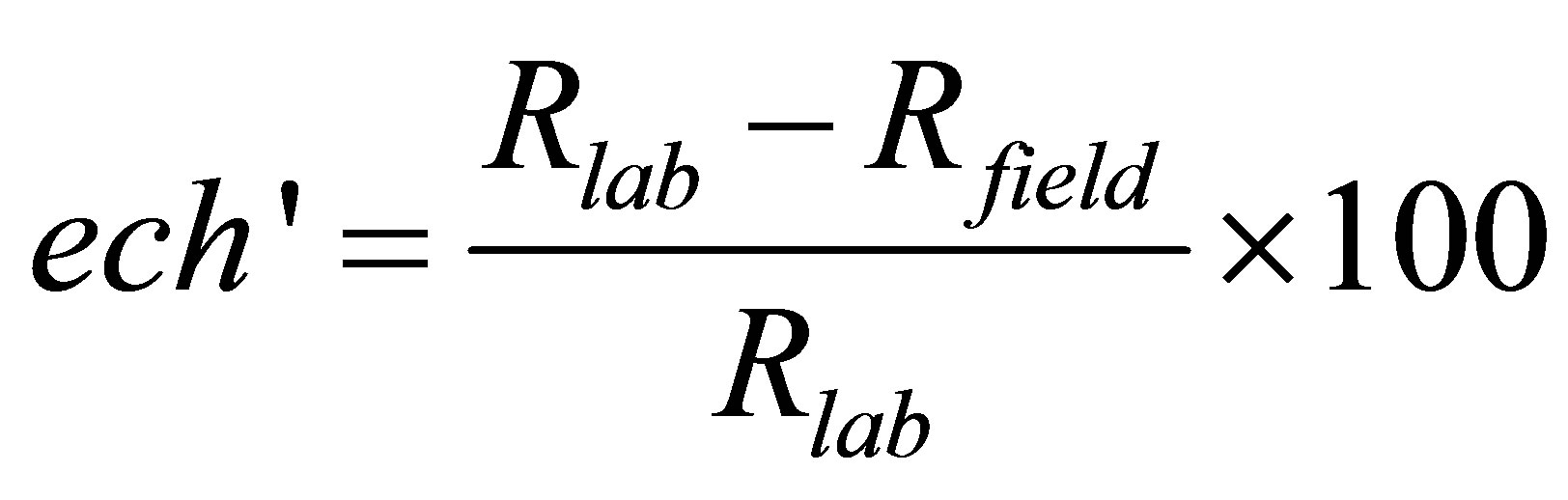 (9)
(9)
For sandstones, this parameter takes high values more than 85%. This coefficient increases remarkably when the rock is most heterogeneous and takes values higher than 93% (Table 3).
6.2. Fractal Geometry
Fractal geometry defines a geometric pattern which is repeated at ever-smaller scales to produce irregular shapes and surfaces which can’t be represented by classical geometry. Configurations of objects are small size, recurrent and can be identified in large range of scale. In Geosciences, this conception is used to quantify a large number of phenomena like spacing of discontinuities, escarpment of asperities and aperture of discontinuities. Due to the tectonic history of Mako, some of filled frac-

Table 1. Evaluation of Scale coefficient (ech) for basalts.

Table 2. Evaluation of Scale coefficients (ech) for sandstones.

Table 3. Evaluation of compression scale coefficient (ech’) for sandstones.
tures and microfractures are folded like the outcrop system. These folds appear on preparation as undulations. For outcrops, folds can’t be identified by simple observations. Determination of orientation of fractures permits to characterize these folds by stereographic representation (Figure 9(a)). In bloc scale, folds can be easily identified (Figure 9(b)) and it is also valid for preparations (Figure 9(c)).
This fractal aspect appears also in the values of Joint Roughness Coefficients (JRC). For results of these studies, JRC values of unfilled microscopic and macroscopic fractures are highest than filled ones. For geological systems, more fractures are former, the more they are filled. Based on this fact, undulated discontinuities (Figure 9) are former. They are folded by posterior orogenesis system, which caused most deformation of the geological materials. Latest events are characterized by fractures, which shear the filled discontinuities. These shears are dextral or senestral like the field ones.
Microdiscontinuities show also same arrangements than macroscopic ones. According to the studied event and the number of iterations, the fractal dimension change. This characteristic is studied in this paragraph. The filled fractures show also conjugate aspects on outcrops and in laboratory scale with same angles and sinuosities (Figure 10).
The Birimian of Kédougou-Kenieba (example of Mako supergroup) inlier shows some shear fractures or faults. In the scale of the field, shears are in many cases represented by stumbles separated by ravines. For microscopic scale, these senestral shears are identified by studing fractures, which crossed another, filled one and which caused displacements (Figure 11). The displacements correspond to the one determined in the field in locality where sample have been taken.
Figure 12 shows filled fractures in the field scale (Figure 12(a)) and on preparation scale (Figure 12(b)). These fractures are filled with chlorite, epidote and calcite. Due to the same nature of filling products and the form of structures at the field and on the preparation, we deduce that they are contemporaries. Spacing of fractures measured for these discontinuities are 5.4 centimeters for rock masses and 175 micrometers for preparations. Before iteration, we consider an element with one discontinuity and one spacing in rock mass scale. After iteration, they are 308 microfractures corresponding to the spacing seen in microscopic scale. For this assemblage of microdiscontinuities, some of them are identified in the preparation. The preparation shows just a number of microfracturation that allows defining the fractal dimension. The fractal dimension associated to this operation is df = 1.12.