1. Introduction
A simple way of extending the class of regular polygons is to maintain the congruence of vertex angles while no longer requiring that the edges be congruent. In this generality, the newly obtained equiangular polygons are not all that interesting given one can find plenty of such (nonsimilar) polygons with a given number of edges. Indeed, drawing a parallel line to one of the edges of a regular polygon through an arbitrary point on an adjacent edge yields a trapezoid and a new equiangular polygon with the same number of edges as the initial one (see Figure 1). However, if we also require that all edge lengths be rational numbers and that at least two of these numbers be different (thus excluding regular polygons), in general, such equiangular polygons may not even exist. For example, if we start with the regular pentagon  and draw the parallel
and draw the parallel  to
to  as in Figure 1 and if
as in Figure 1 and if  and
and  are rational numbers then, except for
are rational numbers then, except for  all edge lengths of the equiangular pentagon
all edge lengths of the equiangular pentagon  are rational. However,
are rational. However,  is irrational. While this, by no means, proves that equiangular pentagons with
is irrational. While this, by no means, proves that equiangular pentagons with

Figure 1. New equiangular pentagons from old.
rational edges must be regular, it gives some credibility to the non-existence claim above.
An interesting investigation of equiangular polygons with integer sides is provided in [1], where the author considers the problem of tiling these polygons with either regular polygons or other pattern blocks of integer sides. In particular, he points out that every equiangular hexagon with integer sides can be tiled by a set of congruent equilateral triangles, also of integer sides, and also proposes a general tiling conjecture with an extended tiling set. On the other hand, if one no longer requires integer edges but asks that the vertices be integer lattice points, the only equiangular polygons that will do are squares and octagons (see [2,3]).
Further restricting the class of equiangular polygons with integer sides, in [4], R. Dawson considers the class of arithmetic polygons, i.e., equiangular polygons whose edge lengths form an arithmetic sequence (upon a suitable rearrangement) and shows that the existence of arithmetic n-gons is equivalent to that of equiangular n-gons whose side lengths form a permutation of the set  In addition, some interesting existence as well as non-existence results are obtained, but the classification problem for arithmetic polygons with an arbitrary number of edges is left open.
In addition, some interesting existence as well as non-existence results are obtained, but the classification problem for arithmetic polygons with an arbitrary number of edges is left open.
In this note, we address the more general problem of determining all equiangular polygons with rational edges and, as a special case, we settle the classification problem above.
2. Preliminaries
First, we derive a necessary and sufficient condition for the existence of closed polygonal paths in terms of edge lengths and angle measures.
Proposition 1 Let  and
and  be positive real numbers with
be positive real numbers with  There exists a closed polygonal path
There exists a closed polygonal path  (with
(with  oriented counterclockwise) having edge lengths
oriented counterclockwise) having edge lengths  and the measures of the angles* formed by
and the measures of the angles* formed by  with
with 
 with
with 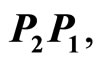
 with
with  equal to
equal to  , respectively, if and only if
, respectively, if and only if
 (1.1)
(1.1)
and
 (1.2)
(1.2)
for some integer 
Proof Assuming that such a polygon exists, let  be the complex number associated to
be the complex number associated to . As the vector
. As the vector  is the
is the  multiple of the rotation of
multiple of the rotation of  in
in  through
through  (see Figure 2), we have
(see Figure 2), we have

Based on the same type of argument, regardless of the orientation of triangles  we have
we have

Combining these relations with

yields

thus proving relation (1.1) from the conclusion. Relation (1.2) follows easily as a consequence of the last relation in the set of  relations above.
relations above.
Conversely, to prove the existence of a closed polygonal path with given  satisfying (1.1), observe that, starting with an arbitrary point
satisfying (1.1), observe that, starting with an arbitrary point  we can always consider the points
we can always consider the points  such that, with the exception of
such that, with the exception of  and the measure of the angles formed by
and the measure of the angles formed by  with
with  and
and  with
with  all edge lengths and angle measures are as needed. We will prove that the closed polygonal path
all edge lengths and angle measures are as needed. We will prove that the closed polygonal path  satisfies the requirements. To do so, if we let
satisfies the requirements. To do so, if we let  and denote the measure of the angle formed by
and denote the measure of the angle formed by  with
with  by
by  and
and  with
with  by
by  then, we need to show that
then, we need to show that  and
and  By applying the direct implication to our polygonal path (with edge lengths
By applying the direct implication to our polygonal path (with edge lengths  and angle measures
and angle measures  ), we have
), we have

Equivalently,
 (1.3)
(1.3)
By factoring out  and applying the modulus on both sides of the equality above, we have
and applying the modulus on both sides of the equality above, we have

However, the same type of operations can also be applied to the relation in our hypothesis (involving 
 ) to obtain
) to obtain

But then  based on the two formulas above. Now, factoring out
based on the two formulas above. Now, factoring out  and replacing
and replacing  by
by  in (1.3), we have
in (1.3), we have
 (1.4)
(1.4)
But we also have
 (1.5)
(1.5)
Comparing relations (1.4) and (1.5), it follows that  To show that
To show that  let’s note that relation (1.2) applied to
let’s note that relation (1.2) applied to  implies
implies

for some integer  By hypothesis,
By hypothesis,

Combining the two relations above finishes the proof.
3. Equiangular Polygons
If we consider a convex equiangular  gon, then, with notations as in the previous section, we have
gon, then, with notations as in the previous section, we have
 In addition, if we let
In addition, if we let
 then, based on Proposition 1, we obtain Theorem 1 Given
then, based on Proposition 1, we obtain Theorem 1 Given  there exists a convex equiangular n-gon with side lengths
there exists a convex equiangular n-gon with side lengths  (listed counterclockwise) iff
(listed counterclockwise) iff

Definition 1 A rational polygon is a polygon all of whose edge lengths are rational number.
Observation 1 The edges of a non-convex equiangular polygon can be rearranged to form a convex equiangular polygon, so we will only concentrate on the latter.
As a consequence of Theorem 1, we obtain Proposition 2 Let  and let
and let  be the degree of the cyclotomic polynomial
be the degree of the cyclotomic polynomial  There exists a convex, rational, equiangular n-gon with edge lengths
There exists a convex, rational, equiangular n-gon with edge lengths  (ordered counterclockwise) iff the following equalities are satisfied:
(ordered counterclockwise) iff the following equalities are satisfied:



where  are defined by
are defined by

for all 
Proof Let us first note that the definition of  makes sense. Indeed, since
makes sense. Indeed, since  forms a basis of
forms a basis of  for a fixed
for a fixed  we can define
we can define 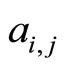 to be the coefficients of
to be the coefficients of  in this basis.
in this basis.
For each  if we replace
if we replace  in the equality from Theorem 1 by
in the equality from Theorem 1 by , we obtain
, we obtain

By reorganizing the terms, the formula above becomes

But then we get a polynomial of degree  with rational coefficients having
with rational coefficients having  as a root. This is only possible iff all the coefficients are zero, thus proving the proposition.
as a root. This is only possible iff all the coefficients are zero, thus proving the proposition.
Observation 2 By fixing  the conditions in the proposition above generate a system of equations
the conditions in the proposition above generate a system of equations

with N equations and  variables
variables  Comparing the number of equations and the number of variables, we obtain three cases depending on whether
Comparing the number of equations and the number of variables, we obtain three cases depending on whether  or
or 
To better understand the three cases above, we have Lemma 1 For any positive integer  we have the following 1)
we have the following 1)  iff
iff  for some odd prime
for some odd prime  and some positive integer
and some positive integer 
2)  iff
iff  for some positive integer
for some positive integer 
3)  iff
iff  where the nonnegative integer
where the nonnegative integer  and the odd integer
and the odd integer  are such that either
are such that either  or, if
or, if  then
then  is the product of the powers of at least two distinct primes.
is the product of the powers of at least two distinct primes.
Proof Since the third case is the complement of the first two, it is enough to prove the first two cases. So let , where
, where  are distinct primes and
are distinct primes and  are nonnegative integers.
are nonnegative integers.
To prove  observe that the inequality
observe that the inequality  is equivalent to
is equivalent to

or  To show that n has the desired form, let us assume by contradiction that
To show that n has the desired form, let us assume by contradiction that  But then, since
But then, since  and
and  we have
we have  or equivalently
or equivalently  This implies
This implies  Together with
Together with  the second inequality above yields
the second inequality above yields  which contradicts the hypothesis. Thus
which contradicts the hypothesis. Thus 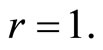 But then we must also have p1 > 2 since otherwise
But then we must also have p1 > 2 since otherwise  Conversely, it is easy to see that if
Conversely, it is easy to see that if  then
then 
For 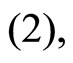 by considerations similar to the ones above we must have
by considerations similar to the ones above we must have  Since, by (1), we cannot have
Since, by (1), we cannot have  it must be that
it must be that  Also, it is clear that if
Also, it is clear that if  then
then 
Next, we consider convex, rational, equiangular polygons in each of the three cases given by the lemma. For the overdetermined case  we have the following:
we have the following:
Proposition 3 If  are the lengths of the edges of a convex, rational,
are the lengths of the edges of a convex, rational,  -gon with p > 2 prime, then the polygon is equiangular iff
-gon with p > 2 prime, then the polygon is equiangular iff

Proof Let

be the minimal polynomial of  over
over  (see [5], page 31). In order to apply Proposition 2, we need to write
(see [5], page 31). In order to apply Proposition 2, we need to write  for all
for all  as a linear combination with integer coefficients of
as a linear combination with integer coefficients of  Starting with the equation in
Starting with the equation in  given by its minimal polynomial and multiplying by
given by its minimal polynomial and multiplying by  we have
we have

Thus,  if
if  and
and  otherwise. With these values of
otherwise. With these values of  the conclusion follows.
the conclusion follows.
Consequence 1 Any rational equiangular polygon with a prime number of edges is regular.
Proof This follows based on Observation 1 and the  case in Proposition 3.
case in Proposition 3.
Observation 3 The consequence above proves conjecture 6 from [4].
For the fully determined case  we have the following characterization:
we have the following characterization:
Proposition 4 Given a convex, rational polygon whose number of edges is a power of two, the polygon is equiangular iff opposite edges are congruent.
Proof Let  be the number of edges of the polygon. Since
be the number of edges of the polygon. Since  it follows that
it follows that
 Thus, the relation from Theorem 1 becomes
Thus, the relation from Theorem 1 becomes

or

But then  is a root of a rational polynomial of degree less than that of
is a root of a rational polynomial of degree less than that of  This is only possible if the polynomial is identically zero, which implies the conclusion.
This is only possible if the polynomial is identically zero, which implies the conclusion.
As a consequence of the proposition above, we obtain a different proof of Theorem 3 from [4].
Consequence 2 There does not exist an equiangular  -gon with integer edge lengths, all distinct.
-gon with integer edge lengths, all distinct.
For the underdetermined case , given the lack of a simple formula for
, given the lack of a simple formula for  in this case, we will only consider the following example.
in this case, we will only consider the following example.
Lemma 2  are the edge lengths of a convex equiangular 15-gon, with the edges ordered counterclockwise, iff
are the edge lengths of a convex equiangular 15-gon, with the edges ordered counterclockwise, iff

and

Proof In this case, 
 By letting
By letting  we have
we have



Based on these relations and Proposition 2, we must have




If we let


and


the relations above become


Clearly, these relations are equivalent to  and
and  thus proving the lemma.
thus proving the lemma.
4. Arithmetic Polygons
Following the terminology from [4], a polygon is said to be arithmetic if it is equiangular and its edge lengths (in some order) form a nontrivial arithmetic sequence. As shown in the same paper, an arithmetic  -gon exists iff there exists an equiangular polygon with edge lengths (in some order)
-gon exists iff there exists an equiangular polygon with edge lengths (in some order)  In this section we find a necessary and sufficient condition for the existence of arithmetic polygons in terms of the number of edges. First, we have the following:
In this section we find a necessary and sufficient condition for the existence of arithmetic polygons in terms of the number of edges. First, we have the following:
Consequence 3 There are no arithmetic polygons whose number of edges is the power of a prime.
Proof This follows as a consequence of Propositions 3, 4, and Observation 1.
One case when arithmetic polygons do exist is provided by the example below.
Example 1 There exists a (convex) arithmetic 15-gon.
Proof If we select

then the conditions in Example 2 are satisfied since

and

Observation 4 The proposition above provides a counterexample to conjecture 7 from [4] claiming that no arithmetic n-gons exist if  is odd.
is odd.
The example above suggests the following:
Theorem 2 There exists an arithmetic n-gon if and only if  is not the power of a prime, i.e.,
is not the power of a prime, i.e.,  has at least two distinct primes factors.
has at least two distinct primes factors.
Proof By Consequence 3, it is enough to prove the converse. So, let’s consider  for some positive integers
for some positive integers  Since
Since  is not the power of a prime,
is not the power of a prime,  and q can be chosen to be relatively prime. If
and q can be chosen to be relatively prime. If  denotes a primitive
denotes a primitive  th root of unity, then
th root of unity, then
 (1.6)
(1.6)
and
 (1.7)
(1.7)
Multiplying relations (1.6) by  and (1.7) by
and (1.7) by  we have
we have
 (1.8)
(1.8)
and
 (1.9)
(1.9)
Let us now observe that every integer between 1 and  appears exactly once as an exponent in both (1.8) and (1.9) due to the fact that p and q are relatively prime. If we add all
appears exactly once as an exponent in both (1.8) and (1.9) due to the fact that p and q are relatively prime. If we add all  equations (1.8) and all
equations (1.8) and all  equations (1.9), we obtain
equations (1.9), we obtain

Whenever 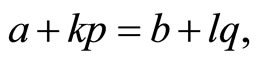 the sum of the corresponding coefficients
the sum of the corresponding coefficients 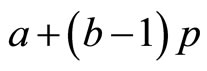 is an integer between 1 and pq Moreover, different
is an integer between 1 and pq Moreover, different  and
and  with
with ,
,  generate different values for
generate different values for  because
because  and
and  are relatively prime. Since there are exactly pq pairs
are relatively prime. Since there are exactly pq pairs  the values of
the values of  will represent a permutation of the set
will represent a permutation of the set 
5. Conclusions
In this note we determined all rational equiangular polygons whose number of sides a prime power. Although we also determined all rational equiangular 15-gons, the general problem remains open. In addition, we provided a complete characterization of arithmetic polygons.
As an interesting application, we note that, as mentioned in [6], there is a nice correspondence arising from the Schwarz-Christoffel transformations between equiangular n-gons and certain areas determined by binary forms of degree n with complete factorizations over  It would be interesting to investigate the consequences of our results in the language of binary forms.
It would be interesting to investigate the consequences of our results in the language of binary forms.
NOTES