Deformation of a two-phase medium due to a long buried strike-slip fault ()
1. INTRODUCTION
The elastic residual field due to a strike-slip fault in various Earth models has been calculated by several investigators e.g. [1-12] and others. In [1], the problem of the static deformation of a multilayered half-space by a long strike-slip line dislocation is considered. In [2], the two-dimensional problem of a long displacement dislocation in an isotropic multilayered half-space is studied. In that paper, authors obtained the surface displacement caused by a line source of arbitrary dip. In [3], authors obtained closed-form analytic expressions for the displacements and stresses at any point of either of two homogeneous, isotropic and perfectly elastic half-spaces in welded contact due to a horizontal or a vertical long strike-slip fault. Reference [4] demonstrated the solution for a long strike-slip fault of arbitrary dip, generalizing the work done in [3]. In [5], authors obtained closedform analytic expressions for the problem of a surfacebreaking long strike-slip fault in an elastic layer overlying an elastic half-space. In [6], authors obtained the deformation field at any point of a horizontal orthotropic elastic layer of infinite lateral extent coupling in different ways such as “welded”, “smooth-rigid”, or “rough-rigid” to a base due to a long blind strike-slip fault. Most of these studies have chosen the interface-breaking fault. The depth of the fault does not occur explicitly in the solution. Therefore, for small dip angles, the fault approaches near the interface and the effect of depth on a fixed dip angle can not be studied independently.
The purpose of present paper is to obtain an analytical solution for the deformation of a long strike-slip fault buried at arbitrary depth located in an elastic, homogeneous, isotropic half-space welded with another elastic, isotropic half-space. The depth occurs explicitly in the solution. Therefore, the effect of the variations in the depth for a fixed dip and vice-versa can be studied directly.
2. THEORY
Let the Cartesian co-ordinates be denoted by  with
with  -axis vertically downwards. Consider a two-phase elastic medium consisting of halfspaces welded along the plane
-axis vertically downwards. Consider a two-phase elastic medium consisting of halfspaces welded along the plane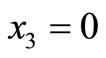 . The upper halfspace
. The upper halfspace 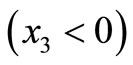 is called Medium I and the lower halfspace
is called Medium I and the lower halfspace  is called Medium II with rigidities
is called Medium II with rigidities , respectively. A long inclined strike-slip fault with strike along
, respectively. A long inclined strike-slip fault with strike along  -axis is situated in the lower halfspace. The upper edge of the fault is taken to be at depth d (Figure 1). Superscript (1) denotes quantities related to the upper half-space and superscript (2) denotes those for the lower half-space.
-axis is situated in the lower halfspace. The upper edge of the fault is taken to be at depth d (Figure 1). Superscript (1) denotes quantities related to the upper half-space and superscript (2) denotes those for the lower half-space.

Figure 1. Geometry of a two-phase elastic medium consisting of half-spaces in welded contact with a long strike-slip fault of width L situated in the lower half-space. d is the depth of upper edge A of the fault,  is the dip angle and s is the distance from the upper edge of fault measured in down-dip direction. The displacement discontinuity on the fault is parallel to x1- axis. The sign
is the dip angle and s is the distance from the upper edge of fault measured in down-dip direction. The displacement discontinuity on the fault is parallel to x1- axis. The sign  indicates displacement in the direction of x1- axis and the sign Θ in the opposite direction.
indicates displacement in the direction of x1- axis and the sign Θ in the opposite direction.
Under the assumption of antiplane strain case, the displacement components are of the form
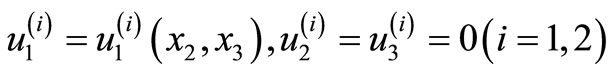 (1)
(1)
For zero body forces, the equilibrium equations reduces to
 (2)
(2)
The displacement field due to a long inclined strikeslip line dislocation parallel to x1-axis and passing through the point (y2, y3) in the lower half-space (medium II) is given by [4]:
 (3)
(3)
 (4)
(4)
where
 = displacement discontinuity (slip)
= displacement discontinuity (slip)
ds = width of the line dislocation
 = dip angle
= dip angle
 = receiver location
= receiver location
 = source location
= source location

 . (5)
. (5)
We write (Figure 1)
 (6)
(6)
where d is depth of the upper edge A of the fault and s is the distance from the upper edge of the fault measured in the down-dip direction. Inserting the values of y2 and y3 from Equation (6) into Equations (3) and (4) and integrating over s between the limits (0, L), we obtain the following expressions for the displacements in the two half-spaces due to an inclined strike-slip fault of finite width L and infinite length:
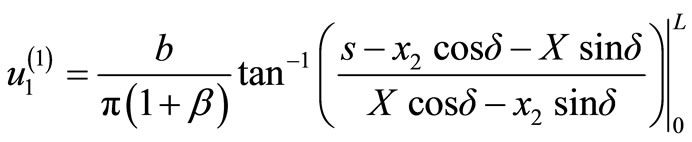 (7)
(7)
 (8)
(8)
where
 (9)
(9)
The non-zero stresses at any point of a two-phase elastic medium are given by
 (10)
(10)
From Equations (7) and (8) and Equation (10), we get the following expressions for the stresses. For the medium I,
 (11)
(11)
 (12)
(12)
and the medium II,
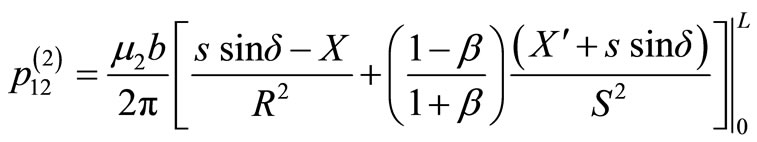 (13)
(13)
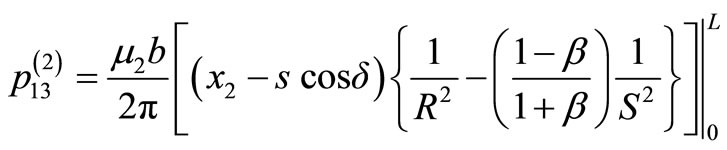 (14)
(14)
where now
 (15)
(15)
Equations (7) and (8) and Equations (11)-(14) give the elastic residual field at any point of two half-spaces due to a long strike-slip fault of finite width dipping at an angle  buried at depth d. On taking d = 0, the results for an interface breaking fault located in the lower halfspace welded with another half-space coincide with the corresponding results of [4]. Also on taking
buried at depth d. On taking d = 0, the results for an interface breaking fault located in the lower halfspace welded with another half-space coincide with the corresponding results of [4]. Also on taking , which implies
, which implies , the results coincide with the corresponding results given by [7] for a uniform half-space due to a vertical strike-slip fault.
, the results coincide with the corresponding results given by [7] for a uniform half-space due to a vertical strike-slip fault.
3. NUMERICAL RESULTS
We have studied the behaviour of the parallel displacements and the stresses numerically. Figure 2(a) shows the parallel displacement  at the interface
at the interface  with the distance from the fault for
with the distance from the fault for  for different values of depth d. Figures 2(b)-(d) are for
for different values of depth d. Figures 2(b)-(d) are for  respectively. We observe that the behaviour of displacement for the interface-breaking fault is altogether different from that for the buried fault. Figures 3(a)-(d) show the variation of parallel displacement
respectively. We observe that the behaviour of displacement for the interface-breaking fault is altogether different from that for the buried fault. Figures 3(a)-(d) show the variation of parallel displacement  with
with 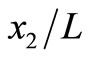 at
at  for three values of depth d = 0, L/2 and 2L for
for three values of depth d = 0, L/2 and 2L for The case d = 0 corresponds to the interface-breaking fault. For the case d = L/2, observer is below the upper edge of the fault and for d = 2L, observer is above the upper edge of the fault.
The case d = 0 corresponds to the interface-breaking fault. For the case d = L/2, observer is below the upper edge of the fault and for d = 2L, observer is above the upper edge of the fault.
In all these figures, there is a discontinuity at  = X cot
= X cot . Figures 4(a)-(d) show the variation of
. Figures 4(a)-(d) show the variation of 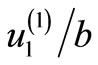 with
with  for different value of d for
for different value of d for 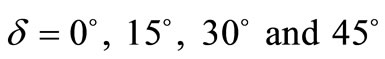 when the observer is in the upper half-space.
when the observer is in the upper half-space.
The contour maps for the shear stress 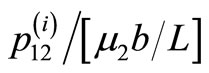 have been plotted in Figures 5(a) and (b) for an interface breaking fault located in the lower half-space welded with another half-space for
have been plotted in Figures 5(a) and (b) for an interface breaking fault located in the lower half-space welded with another half-space for  and 45˚. Solid lines indicate positive values and dashed lines negative values.
and 45˚. Solid lines indicate positive values and dashed lines negative values.
The values are shown in units of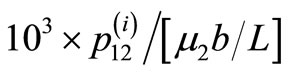 . Heavy line denotes the fault. The shear stress
. Heavy line denotes the fault. The shear stress  is discontinuous at the interface.
is discontinuous at the interface.
Figures 6(a) and (b) are for the buried strike-slip fault d = L for  and 45˚, respectively. The contour maps for the shear stress
and 45˚, respectively. The contour maps for the shear stress  are shown in Figures 7(a) and (b) for interface-breaking fault d = 0 for
are shown in Figures 7(a) and (b) for interface-breaking fault d = 0 for  and 45˚. The stress is continuous at the interface. The values are shown in units of
and 45˚. The stress is continuous at the interface. The values are shown in units of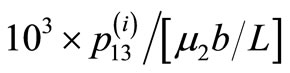 . Figures 8(a) and (b) are for the buried fault d = L.
. Figures 8(a) and (b) are for the buried fault d = L.
4. DISCUSSION
The results presented in this paper are significant
for obtaining the deformation due to an inclined strikeslip fault located at an arbitrary depth and arbitrary dip angles. In the earlier paper [4], the results are obtained for d = 0. Therefore, for small dip angles, the fault approaches near the interface. In the present paper, the depth d is taken explicitly. The effect of variation in depth for a fixed dip and vice-versa can be studied independently.
5. ACKNOWLEDGEMENTS
One of the authors SR is thankful to University Grant Commission, New Delhi for financial support in the form of Major Research Project.