1. Introduction
The increasing amount of fluoride, nitrate and sulfate in water and wastewater and their implication in environment and health lead an important interest in their removal [1-6]. Fluoride, nitrate and sulfate removal can be carried out by membrane separation, ion exchange, adsorption process, chemical treatment, etc. [7-9]. Amongst them, adsorption is simpler and effective for this treatment. Resins and membranes are considered the most promising adsorbents [8,9].
Processes for ion removal using ion exchange resins and membranes have been developed by different authors [10-13]. They found that ion removal using ion exchange resin and membrane has good potential for industrial wastewater treatment. Several studies on the adsorption of ions on ion exchange resins such as IR 120, Dowex A-1, Duolite GT-73 [14], IRN77 [15], Amberlite IRN 9766 [1], Lewatit K 6362 [3], Amberlite IRC 748 [16] have been reported.
Shi, et al. [17] investigated equilibrium sorption for the removal of hexavalent chromium from aqueous solutions by adsorption on D301, D314 and D354 anion exchange resins. Chabani, et al. [18] studied the removal of nitrate ions from aqueous solutions by strong anion exchange resin Amberlite IRA 400. The experimental data have been analysed using the Langmuir, Freundlich, RedlichPeterson and Sips isotherms models. They found that the Sips model was found to give the best fit of the adsorption isotherm data in a wide range of pH.
In recent years, Haghshenoa, et al. [3] studied the removal of sulfate anions from industrial wastewater by adsorption on Lewatit K 6362 resin. This study was carried out to determine the adsorption equilibrium data and the relation of adsorption isotherms. Isothermal data can be fitted with Freundlich adsorption isotherms better than Langmuir equation. In another report, Wawrzkiewicz and Hubicki [19], analyzed the removal of tartrazine from aqueous solutions by strongly basic polystyrene anion exchange resins and they found that Amberlite IRA-900 and Amberlite IRA-910 resins can be used as the adsorbent for the removal of tartrazine from its aqueous solutions.
Recently, Kusumaningsih, et al. [20], investigated equilibrium and kinetic parameters for the adsorption of Cr(III) and Pb(II) on cation exchange resin. Their results showed that this resin is an effective adsorbent for Cr(III) and Pb(II), though Cr(III) adsorption was more favorable than that of Pb(II) and Langmuir type sorption isotherm was suitable for their equilibrium studies.
On the other hand, a number of ion exchange membrane have been used in order to remove ions from water. Nevertheless, Lin and Suen [21] studied the separation of proteins by adsorption on cation exchange membranes (P81) and anion exchange membranes (DE81). For the batch adsorption results, the Suen model is found to fit better than the Langmuir model, indicating the heterogeneous adsorption for proteins onto ion exchange membranes.
Adsorption on ion exchange membrane has been studied by Do Hee, et al. [22] to remove natural organic matter from water because it has been found to be a problematic solute for the electrodialysis. Furthermore, removal of anionic reactive dyes from water has been realized by Chia-Hung, et al. [13]. They studied the adsorption of Cibacron blue 3GA and Cibacron red 3BA as anionic reactive dyes using two types of commercial anion exchange membranes, strong basic (SB6407) and weak basic (DE81). Another study [12] has been reported in order to remove cationic dye from water by adsorption on cation exchange membrane. The adsorption data of dye were analyzed by the Langmuir and Freundlich isotherms.
The present study deals with the adsorption of fluoride, nitrate and sulfate on AFN membrane The Freundlich, Langmuir, Dubinin-Redushkevich and Temkin equation models are used to fit the experimental equilibrium isotherm data obtained. Three kinetic models, namely the first order, the second order and Elovich kinetic models, were applied to the adsorption of the studied anions on AFN membrane and the rate of kinetics and equilibrium parameters were determined and compared. Thermodynamic parameters such as enthalpy change, free energy change and entropy change for the adsorption system were calculated at 283, 298 and 313 K, respectively.
2. Materials and Methods
2.1. Anionic AFN Membrane
In this investigation, the AFN anion exchange membrane produced by TOKUYAMA SODA was used. The base polymer of this membrane is styrene and divinylbenzene, and the ionic fixed sites are quaternary ammonium groups, so the membrane is a strong anion exchanger. The main characteristics of this membrane are collected in Table 1 and the manufacture data were completed by the determination of the humidity percentage and the ion exchange capacity. The methodology has already been described in previous papers [23,24].
Before experiments the membrane was conditioned with 0.1 mol∙L−1 HNO3 and HCl to remove impurity from the membrane and to convert the exchange sites to the desired ionic form. The conditioned of the AFN membrane was made according to the standard NF X 45 - 200 French Normalization Association procedure [25] for ion-exchange membranes.
2.2. Reagent
The solution of fluoride, nitrate and sulfate used in this study was prepared by dissolving an accurate quantity of NaNO3, NaF and Na2SO4 in ultrapure water.
2.3. Ionic Chromatography
Anions were determined by ionic chromatography using a Metrohm 792 compact IC with a conductivity detector and chemical suppression, a Metrosep a supp 1 (6.1005.300) column, and an eluent of 3 mmol×L−1 sodium carbonate at 1 mL×min−1.
The feed solutions were prepared from reagent grade chemicals and deionized water.
3. Results and Discussion
3.1. Humidity Percentage and ion Exchange Capacity of the AFN Membrane
Humidity percentages values for the AFN membrane in 
form are given in Table 2. Obtained results show that humidity percentage varies with the ionic form of the membrane. This is ¶th can be interpreted by the fact that the humidity percentage of ion exchange membrane depends on a number of different parameters, such as the membrane matrix, the nature of the counter-ions, their charge and their size [26]. It can be shown that the humidity percentage increases with the decreasing of the ionic radius of the counter-ion as given in Table 2.
The ion exchange capacity of AFN membrane in 
and 
form was determined. It was found to be 2.30 meq×g−1 and 2.32 meq×g−1 for the membrane, respectively, in 
and 
form. This result confirms that the ion exchange capacity is independent from the nature of the counter-ion [27].
3.2. Kinetic Studies
The adsorption kinetics is an important factor to predict the rate at which the adsorbate is removed from the solution [28].
Batch experiments were carried out at a constant temperature (298 K) for measuring the adsorption kinetics of
Table 1. Important properties of AFN.
Table 2. Humidity percentage of the AFN membrane.
fluoride ions. The membrane sample (25 cm2) was immersed in a stirred fluoride aqueous solution of given concentration. The mixtures inside the conical flasks were shaked by a shaker and samples were withdrawn at desired time intervals. The sorption capacity at time t, qt (mg/g) was obtained as follows:
(1)
where C0 (mg×L–1) and Ct (mg×L–1) are, respectively, the initial fluoride concentration and the concentration at time t; V is the volume of solution and m the mass adsorbent.
The effect of contact time on the adsorption efficiencies of fluoride on the AFN membrane is shown in Figure 1.
It was found that the uptake of fluoride increases with the lapse of time. However, the adsorption of fluoride was rapid in the first time after which the rate slowed down as the equilibrium approached. This can be explained by the fact that the number of free active sites on the surface of the membrane decreases over time.
The kinetic curve in Figure 2 can be described by suitable kinetic models. The literature reports several kinetic models. In this study, the adsorption kinetic data of fluoride were analyzed using three types of sorption kinetic models. The Lagergren first order model, the second order model and the Elovich model were the three types of kinetic models.
The Lagergren first order expression [29] is written as:
(2)
where qe and qt are the amount of fluoride adsorbed (mg×g–1) at equilibrium and at time t (min), respectively, and k1 is the Lagergren rate constant (min–1).
The plot of log(qe – qt) vs. t is shown in Figure 2, from which k1 and qe can be obtained, respectively, from the slope and the intercept.
The linearized form of the Lagergren second order model [30] can be given by the following equation:
(3)
where k2 is the equilibrium rate constant of second order adsorption (g×mg–1×min–1).
The Lagergren second-order plot is shown in Figure 3. Similarly, the model parameters qe and k2 values can be calculated from the slope and intercept.
The Elovich model is one of the most used models to verify and describe the chemisorption during adsorption [31,32]. This model is expressed by the following equation:
(4)
where a is the initial adsorption rate (mg×g–1×min–1), β is the desorption constant related to the extent of surface
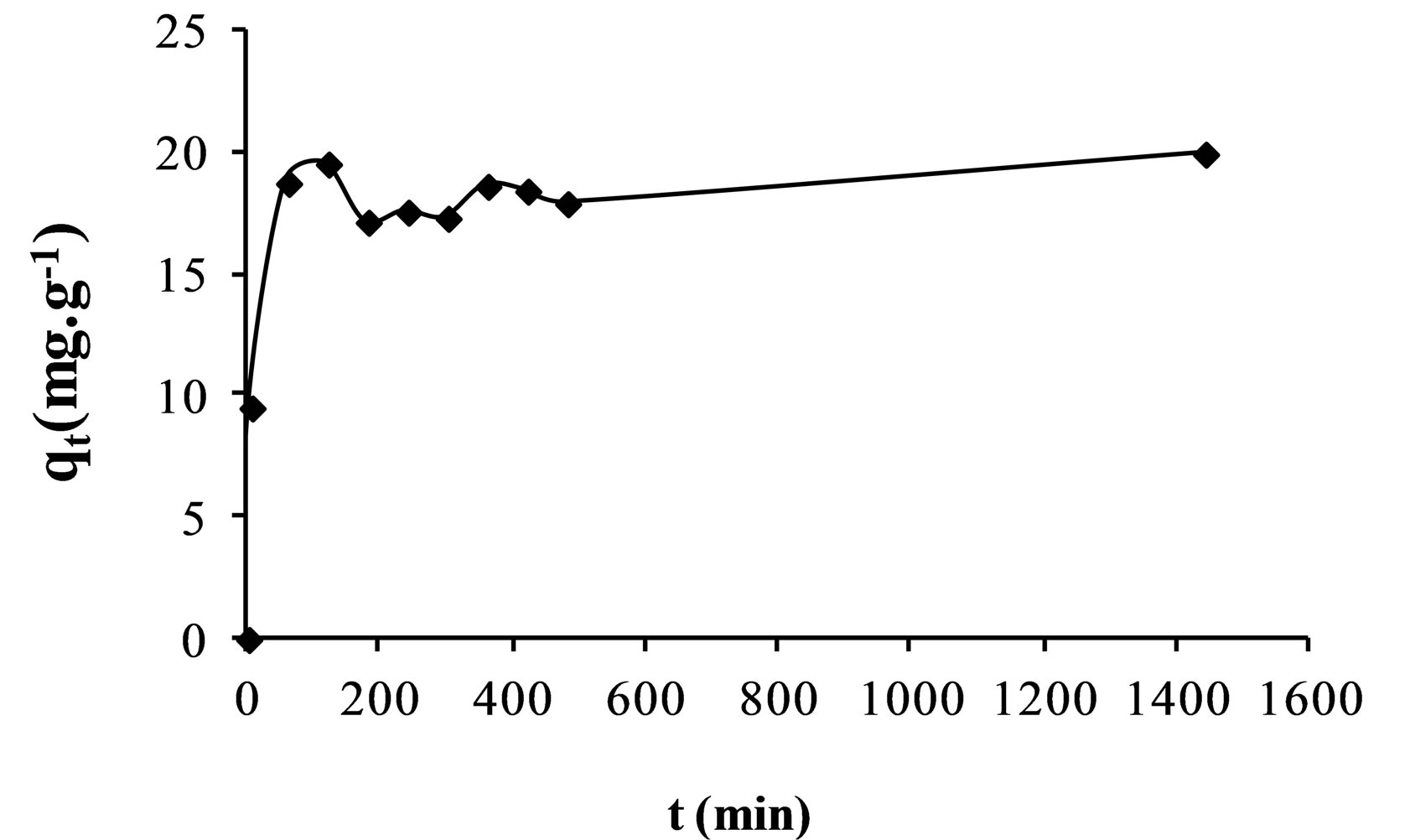
Figure 1. Modelling of sorption of fluoride ions onto AFN membrane.
Figure 2. First order kinetic plot for the adsorption of fluoride ions onto AFN membrane at 298 K.
coverage and the activation energy for chemisorptions. The plot of the Elovich equation is shown in Figure 4.
The correlation coefficients and the kinetic constant for the adsorption of fluoride on the AFN membrane for the studied models are given in Table 3.
Obtained results show that the initial rate of adsorption of fluoride on the AFN membrane at 298 K, determined from the product 
is about 1.487 mg×g–1×min–1.
According to the results obtained in Table 3, we note that the Lagergen second-order model is the most reliable way to determine the order of the kinetics adsorption, since it has the best correlation coefficient (R2 = 0.997). The value of qe calculated by this model (qe = 18.18 mg×g–1) is very similar to that given by the experimental results (qe = 19.90 mg×g–1). A similar phenomenon has been observed for the adsorption of fluoride on ion exchange resin Ceralite IRA 400 (quaternary ammonium) [33].
3.3. Sorption Studies
Adsorption isotherms of 
were obtained by batch experiments at various temperatures (from 283 to 313K). Several samples of the AFN membrane were added to each flask containing fluoride, nitrate or sulfate solutions of various concentrations. The pH values of the mixture were approximately 6.7 and did not vary significantly with the dilution. All flasks were
Figure 3. Second order kinetic plot for the adsorption of fluoride ions onto AFN membrane at 298 K.
Figure 4. Plot of Elovich model kinetics at 298 K.
Table 3. Kinetic parameters for the adsorption of F− on AFN membrane.
then sealed to minimize evaporation, and shaked at 150 rpm in a thermostatic bath. Preliminary tests showed that the adsorption was complete after 6 h.
The concentration of anions at equilibrium was determined by ionic chromatography and the amount of adsorption at equilibrium, qe (mg∙g−1), was given by:
(5)
where Ce (mg×L–1) is the initial anion concentration at equilibrium.
The adsorption isotherms were plotted between the amount of anion adsorbed per gram of membrane, qe, and the amount of anions left in equilibrium solution, Ce. Adsorption isotherms obtained at different temperatures are given in Figure 5.
Obtained isotherms shown that the adsorption capacity increased with the equilibrium concentration of the ion in solution. It was also shown that the adsorption amount of 
increase with increasing temperature.
Adsorption isotherm describes the relationship between the amount of adsorbate adsorbed on the adsorbent and the concentration of adsorbate at equilibrium. Several adsorption isotherm equations are available to describe the adsorption equilibrium and the four important isotherms selected in this study are Freundlich [34], Langmuir [35], Dubinin-Radushkevich (D-R) [36] and Temkin [37] models. The linear form of the equation is shown in Table 4.
Figure 5. Adsorption isotherms of nitrate (a); sulfate (b) and fluoride (c) ions on AFN membrane.
The Freundlich model, which is an indicative of the surface heterogeneity of the sorbent. The Freundlich adsorption isotherms for the fluoride, nitrate and sulfate adsorption at different temperature (from 283 K to 313 K) was given in Figure 6.
However, Langmuir model is probably the best known and most widely applied sorption isotherm. It assumes that sorption takes place at specific homogeneous sites within the adsorbent [35].
Figure 7 indicates Langmuir isotherms fitted to the equilibrium adsorption data at different temperatures.
The values of Freundlich and Langmuir parameters are reported in Table 5. Both Freundlich and Langmuir isotherms fitted with a correlation coefficient greater than 0.98.
Based on Table 5, it seen that the maximum adsorption capacity 
of the membrane increase with rise in temperature which confirmed the preference of high temperature for adsorption. The increase in adsorption capacity of the membrane at higher temperature may be attributed to activation of the membrane surface.
Freundlich constants 
and 1/n were also influenced by temperature. For studied tempeatures 1/n values are less than unity indicating favorable adsorption.
In order to predict the adsorption efficiency of the adsorption process, the separation factor, RL, of the Langmuir model was determined by using the following equation:
(6)
The RL values are calculated in Table 6. Obtained results show that the values of RL are less than unity which indicate a favorable adsorption of fluoride, nitrate and sulfate ions on the AFN membrane. This result was confirmed by the values of 1/n is less than unity indicating a favorable adsorption.
Table 4. Isotherm constants for two-parameter models by linear regression.
Table 5. Adsorption isotherm constants for nitrate, sulfate and fluoride on AFN membrane.
Figure 6. Freundlich isotherm plots for the adsorption of nitrate (a); sulfate (b) and fluoride (c) ions by the AFN membrane.
Figure 7. Langmuir isotherm plots for the adsorption of nitrate (a); sulfate (b) and fluoride (c) ions by the AFN membrane.
Figure 8. Dubinin-Radushkevich (D-R) isotherm plots for the adsorption of nitrate (a); sulfate (b) and fluoride (c) ions by the AFN membrane.
Table 6. Values of the separation factor RL.
The adsorption data was applied to the DubininRadushkevich model in order to distinguish between physical and chemical adsorption. D-R isotherms are presented in Figure 8 by plotting Lnqe versus ɛ2 which shows the linear graphs for the sorption of fluoride, nitrate and sulfate.
The Temkin adsorption isotherms for the fluoride, nitrate and sulfate adsorption are obtained by plotting graph qe versus LnCe, as given in Figure 9.
The parameters of Temkin and Dubinin-Radushkevich adsorption isotherms evaluated from the linear plots are presented in Table 7.
The Temkin isotherm contains a factor that explicitly takes interactions between adsorbing species and adsorbates into account [38]. The Temkin constants listed in Table 7 show that adsorption heat (b) decreases with increase in temperature for adsorption of fluoride and sulfate.
For the Dubinin-Radushkevich model, the magnitude of the adsorption energy, E, is useful for estimating the adsorption process type. It was found to be in the range of 0.697 - 3.580 kJ/mol, which is less than the energy range corresponding to the physical adsorption reactions, 8 - 16 kJ×mol–1 [39]. Thus, it is concluded that an adsorption type of fluoride, nitrate and sulfate on AFN membrane is a physical adsorption. The linear correlation coefficients for the Langmuir, Freundlich, Temkin and D-R adsorption isotherms are given in Table 8.
Obtained results show that the best regression for the adsorption of fluoride, nitrate and sulfate on AFN membrane are obtained with the linearization of Langmuir isotherm.
3.4. Thermodynamic Studied
Based on the obtained results, the variations of thermodynamic functions for the adsorption of
such as standard free energy
, standard enthalpy 
and standard entropy 
were determined using the following equations:
(7)
where R is the universal gas constant (8.314 J/mol×K), T is absolute temperature.
can be also defined as:
(8)
The combination of equation (7) and (8) gives the following equation which can be used to determine the
Figure 9. Temkin isotherm plots for the adsorption of nitrate (a); sulfate (b) and fluoride (c) ions by the AFN membrane.
thermodynamic parameters 
and
:
(9)
The values of DHo and DSo were obtained from the slope and intercept of the plots of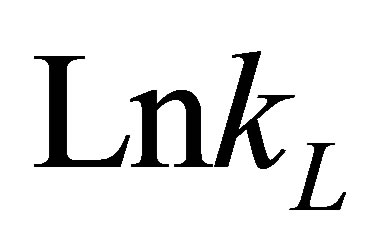 
versus 
(Figure 10) are given in Table 9.
For the adsorption of fluoride the entropy change 
values is negative which correspond to the decrease of randomness at the solid solution interface during the adsorption. While, for the adsorption of nitrate and sulfate the positive values of adsorption entropy corresponds to an increase in randomness.
The obtained values of the enthalpy change indicate that the adsorption of fluoride is exothermic (negative) and endothermic for the adsorption of nitrate and sulfate (positive).
Obtained results show that the standard free energy during the sorption process at all studied temperatures were negative, corresponding to a spontaneous process of fluoride, nitrate and sulfate ions sorption onto AFN membrane.
The 
values suggest the following order of affinity of the membrane for the studied anions. Obtained results show that at 283, the affinity order is:
. This order is: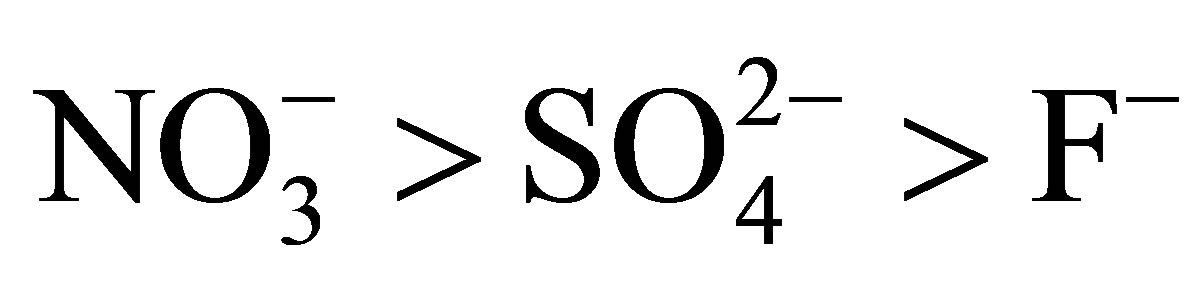 
at 298 K and 313 K.
4. Conclusion
The kinetic, thermodynamic and equilibrium isotherm tests were conducted at 283, 298 and 313 K. The adsorption process followed the second-order reaction. The regression analysis of the equilibrium data fitted the Langmuir, Freundlich, Dubini-Redushkevich and Temkin adsorption isotherm models. The Langmuir model has better correlation coefficients than the other model. The Langmuir adsorption theory best describes fluoride, nitrate and sulfate adsorption on AFN membrane. The Dubini-Redushkevich model indicates the presence of a physical sorption model.