Pseudosymmetric Features and Nonlinear Optical Properties of Potassium Titanyl Phosphate Crystals

Anastasia P. Gazhulina, Mikhail O. Marychev

Lobachevsky State University of Nizhni Novgorod, Nizhni Novgorod, Russia.

DOI: 10.4236/csta.2013.23015                

Abstract

A number of publications containing structural data, characteristics of nonlinear optical properties of pure and doped crystals of potassium titanyl phosphate (KTP) family have been reviewed to analyze the structural and symmetry conditionality of nonlinear optical properties of these crystals. The pseudosymmetric features of KTP-type crystals with respect to inversion are investigated. Specifically, pseudoinversion distribution maps are calculated; pseudoinversion extrema and coordinates of pseudoinversion centres are found; and the distributions of pure and doped KTP-type structures and their individual atomic sublattices over the degree of pseudoinversion are analyzed. A correlation between the characteristics of nonlinear optical properties of a number of crystals belonging to the KTP family and the degree of pseudoinversion of their atomic structures is demonstrated.

Keywords

Potassium Titanyl Phosphate Family; Pseudosymmetry; Nonlinear Optical Properties

1. Introduction

Study of the relationship of structural and symmetric features of crystals with their physical properties is an urgent problem of condensed-matter physics. Point symmetry determines the set of possible physical properties of crystals, primarily, in correspondence with the Neumann principle. The symmetric features of atomic structures of crystals can be characterized more completely taking into account the phenomenon of pseudosymmetry, which makes it possible to establish finer relationships of the structure-property type. Fedorov pseudosymmetry of crystals [1] is the phenomenon of invariance of a considerable part of the crystal atomic structure (part of electron density and (or) subsystem of atomic nuclei) with respect to some group of symmetry operations compatible with the lattice (with respect to some supergroup of the symmetry space group of crystal).

The pseudosymmetry of a specific structure can quantitatively be characterized by the degree of invariance (degree of pseudosymmetry) of its total electron density r(r) with respect to some isometric operation [1,2]:

. (1)

Integration in Equation (1) is performed over the volume V of crystal unit cell. If is not a symmetry operation for the function r(r), the degree of pseudosymmetry < 1; however, if r(r) is symmetric with respect to the operation, reaches a maximally possible value: unity.

The second-order susceptibility of crystal determines the intensity of generation of the second optical harmonic and is a structureand symmetry-sensitive property of crystal. For centrosymmetric crystals, the second-order susceptibility should be zero. One might suggest that reduction of symmetry will lead to some dependence of the second-order susceptibility of crystal on the degree of invariance of crystal structure with respect to inversion.

2. Nonlinear Optical Properties of Potassium Titanyl Phosphate Crystals: A Review

The family of crystals with potassium titanyl phosphate (KTP) structure includes more than 100 compounds [3,4]. Their general formula can be written as MM’OXO₄, where M = K, Rb, Na, Cs, Tl, NH₄; M’ = Ti, Sn, Sb, Zr, Ge, Al, Cr, Fe, V, Nb, Ta, Ga; X = P, As, Si, Ge. Interoctahedral (M’-O-M’) oxygen atoms can be replaced with OHand F-; the resulting compounds with the general formula MM’(F,OH)XO4 also belong to the KTP family. The structure of KTP crystals is described by the space group Pna2₁.

We considered 118 crystals belonging to the KTP family, including 29 pure and 89 doped ones. Information about the nonlinear optical characteristics of 108 crystals was found in the corresponding publications. All crystals under consideration were separated into three groups with respect to the available data on their structure and nonlinear optical properties; the relationship between these groups is clearly shown in Figure 1.

The characteristics of nonlinear optical properties of KTP crystals are listed in Table 1, where the parameter I/I_reference is the ratio of second harmonic intensities from a sample under study studied and a powder sample of reference crystal.

The characteristics of nonlinear optical properties were determined in [8,10,11,24] by the Kurtz-Perry method [26] and in [3,5-7,12,14,19,22] by the method described in [27]. The components of the second-order susceptibility tensor were found in [16,17,20] using the Maker fringe technique [28,29].

With allowance for the results of our analysis of the corresponding publications, we can select crystals whose characteristics of nonlinear optical properties are comparable with those for KTiOPO₄ crystal (K_0.5Rb_0.5TiOPO₄, RTA, K_0.966Ti_0.966Nb_0.034OPO₄, K_0.921Ti_0.921Nb_0.079OPO₄, RTP, K_0.99Ti_0.99Sb_0.01OPO₄, KTi_0.96Zr_0.04OPO₄, TTP, KTi_0.9975V_0.0025OPO₄, K_0.5Ti_0.5Nb_0.5OPO₄, CTA, K_0.5Ta_0.5Ti_0.5OPO₄, KTiO(PO₄)_0.5(AsO₄)_0.5, TTA, KTi_0.7Nb_0.3OP_0.7Si_0.3O₄, KTi_0.65Nb_0.35OP_0.65Si_0.35O₄, KTi_0.6Nb_0.4OP_0.6Si_0.4O₄, RbTi_0.98Nb_0.02OPO₄, Na_0.87K_0.13TiOAsO₄, KTi_0.7Nb_0.3OAs_0.7Si_0.3O₄, KTi_0.6Nb_0.4OAs_0.6Si_0.4O₄ RbTi_0.927Nb_0.056Er_0.017OPO₄) and crystals with characteristics of nonlinear optical properties exceeding those of KTiOPO₄ crystal (KTA, K_0.98Ti_0.98Nb_0.02OPO₄, K_0.96Ti_0.96Nb_0.04OPO₄, K_0.97Ti_0.97Sb_0.07OPO₄, K_0.88Ti_0.98Zr_0.06OP_0.99O₄, K_0.88Ti_0.93Zr_0.11OP_0.99O₄, K_0.97Ti_0.99OAs_0.53P_0.49O₄, KTi_0.9Nb_0.1OP_0.9Si_0.1O₄, K_0.80Ti_0.26Zr_0.78OAs_1.01O₄, KTi_0.9Nb_0.1OAs_0.9Si_0.1O₄, K_0.94Nb_0.12Ti_0.91OAs_0.89Ge_0.09O₄, KTi_0.8Nb_0.2OAs_0.8Si_0.2O₄, K_1.02Nb_0.25Ti_0.76OAs_0.75Ge_0.23O₄, K_0.68Rb_0.32TiOPO₄, Cs_0.5K_0.5TiOAsO₄, KTi_0.97Zr_0.03OPO₄, K_0.54Li_0.46TiOAsO₄, K_1.03Nb_0.52Ti_0.48OAs_0.48Ge_0.51O₄, Rb_0.855Ti_0.955Nb_0.045OPO₄, KNb_0.52Ti_0.48OAs_0.48Ge_0.51O₄, RbTi_0.96Nb_0.04OPO₄, K_0.98Nb_0.46Ti_0.56OAs_0.58Ge_0.39O₄).

There are data in the literature on KTiOPO₄ crystals doped with Nb [30-36], Ge [37], Sn [33,38-40], Zr [41- 43], Sb [35,44,45], Ta [35], Fe [46], Hf [47], and Zn [48] and RTP crystals doped with Cs [49] and Zr [50,51]. It was indicated in [39] that an increase in the Sn content leads to a dramatic decrease in the output second-harmonic intensity to zero. The intensity of second-harmonic generation (SHG) for KTi_1-xZr_xOPO₄ crystals reaches a maximum at x = 0.28, where it is more than doubled in comparison with the KTiOPO₄ sample [41]. The SHG intensity increases with an increase in the zirconium content in RbTi_1-xZr_xOPO₄ crystals; at x = 0.034, it rises by 40% [50]. The SHG intensity increases by approximately 35% in comparison with pure KTiOPO₄ samples after replacement of 6% titanium atoms with hafnium [47]. RbTi_1-xTa_xOPO₄ and RbTi_1-xNb_xOPO₄ crystals were investigated in [52], as well as Yb-doped RbTi_1-xTa_xOPO₄ crystals and RbTi_1-xNb_xOPO₄ crystals doped with Yb, Ln and Er. KTiOPO₄ crystals doped with transition metals and RTA crystals doped with lanthanides were studied in [53]. A number of compounds (RbTi_0.98Er_0.01Nb_0.01OAsO₄, RbTi_0.96Er_0.02Nb_0.02OAsO₄, and KTi_0.98Cr_0.02O_0.98F_0.02PO₄, KTi_0.99Fe_0.01O_0.99F_0.01PO₄ RbTi_0.98Er_0.02O(AsO₄)_0.98(SO₄)_0.02) exhibited an increase in the SHG intensity in comparison with RTA and KTP crystals, respectively.

3. Analysis of the Degree of Invariance of the Structure of KTP Crystals with Respect to Inversion

The complete characteristic of pseudosymmetry of any crystal under study with respect to inversion is a threedimensional distribution map of the degree of structural invariance (electron density) with respect to this operation (hereinafter, pseudoinversion), calculated for different positions of inversion points within their unit cell. These maps were obtained with scanning steps over the unit-cell axes a, b, and c chosen to be 0.05 of the cor responding unit-cell parameters. For 118 crystals (Figure 1) with known structure, we calculated three-dimensional pseudoinversion maps using equation (1). The calculations were performed using the computer program and technique described in [54]. Within this approach the electron density function is expanded in a Fourier series in structural amplitudes ([1], see Formulas (5) and (6)).

Figure 2 presents typical examples of cross sections of three-dimensional distribution maps of the degree of pseudoinversion for the structures of KTiOPO₄, KSnOPO₄, KTiOAsO₄, Cs_0.625K_0.375TiOAsO₄ crystals (cuts by the plane z = 0.25). For the structures presented in Figure 2, the origin of coordinates is chosen on the two fold screw axis, and the coordinates of pseudoinversion peaks on the x and y axes are 0.25. We chose cuts by the plane z = 0.25 in Figure 2 because the z coordinate of the pseudoinversion peaks for the structures of the aforementioned crystals is also 0.25.

This situation is typical of most structures under study; in KTP crystals is accompanied by a phase transition to the centrosymmetric space group Pnan. Indeed, having

Figure 1. Groups of KTP crystals under consideration.

Table 1. Characteristics of nonlinear optical properties of KTP crystals.

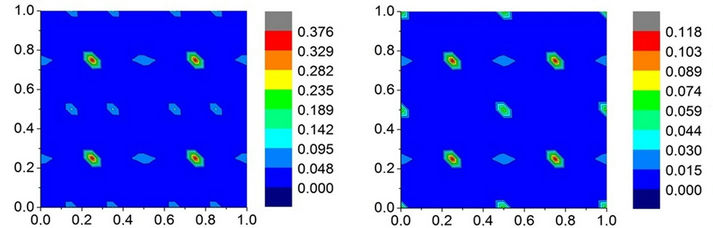(a)(b)

Figure 2. Cut of three-dimensional distribution maps of the degree of pseudoinversion of crystal structure by the plane z = 0.25: (a) KTiOPO₄ (CSD-№ 20970); (b) KSnOPO₄ (CSD-№ 68706); (c) KTiOAsO₄ (CSD-№ 202158); and (d) Cs_0.625K_0.375TiOAsO₄ (CSD-№ 74595).

added inversion to the set of symmetry operations of the space group Pna2₁, which describes the structure of KTP crystals at room temperature, we obtain the group Pnan, where the inversion centre with respect to the twofold screw axis has coordinates (0.25, 0.25).

Thus, in the polar phase of KTP structures, the pseudoinversion peaks are located specifically at inversion centres of these crystals in their high-symmetry nonpolar phase. With allowance for this circumstance, we will characterize the pseudosymmetry of the electron density in each crystal with a known structure by the maximum value of pseudoinversion h_max in the three-dimensional map, and the point with the coordinates corresponding to the found h_max values will be referred to as pseudoinversion centres.

Since the origin of coordinates is arbitrarily chosen in X-ray diffraction analysis, the coordinates of the pseudoinversion centres may differ from 0.25. In the Pna2₁ group [55], the origin of coordinates on the z axis can be chosen at any point, while in the directions of the x and y axes it may lie either on the twofold axis or at the intersection of mirror planes; therefore, the x and y coordinates of pseudoinversion centres can be either (0.25, 0.25) or (0, 0).

To refine the coordinates of pseudoinversion centres and h_max values, we additionally calculated the distribution of the degree of pseudoinversion with a relative scanning step of 0.025 over the unit cell axes. Fixed refined x and y coordinates of pseudoinversion centres were used for repeated calculation of pseudoinversion distribution along the z axis with a relative scanning step of 0.001.

Table 2 contains the maximum pseudoinversion values h_max and coordinates of pseudoinversion centres z(h_max) for a number of KTP structures.

Figures 3(a) and 3(b) show the distribution histograms for the degree of pseudoinversion h_max for pure and doped KTP crystals.

The distribution of pure KTP crystals over pseudoinversion is fairly uniform. As is indicated in Table 2, the mean value < h_max > for them is 0.606. The situation for doped crystals is different: the pronounced maximum in the histogram in Figure 3(b), which amounts to 31%, lies in the range of pseudoinversion values of 0.4 - 0.5, which is followed by a sharp falloff. Therefore, the fraction of pseudo-centrosymmetric structures among doped KTP crystals is very small. The mean value < h_max > for doped crystals is 0.490. Thus, doped KTP crystals are “less symmetric” with respect to inversion than pure compositions.

For the crystals listed in Table 2, along with the calculations of the pseudoinversion of their structures as a whole, pseudoinversion extrema for sublattices of individual types of atoms (h_max(sublattices)) were also calculated. Pseudoinversion was calculated for the pure sublattices of all 118 crystals in Table 2; the distribution histogram of the corresponding extrema is shown in Figure 3(c). For 89 doped crystals in Table 2, the results of similar calculations for Mand M’-type sublattices containing doped atoms are presented as histograms in Figure 3(d). The histograms in Figure 3(c) indicate that the sublattices of Х, О, and F atoms are most pseudocentrosymmetric, sublattices of M-type atoms are least pseudo-centrosymmetric, and the pseudoinversion of the M’ sublattice is intermediate (< h_max(X) ≥ 0.857, < h_max(O) ≥ 0.720, < h_max(F) ≥ 0.870, < h_max(M ) ≥ 0.395, < h_max(M’) ≥ 0.661).

In the presence of impurities, the general view of the histogram for the M’ sublattice (Figure 3(d)) barely differs from that in Figure 3(c); its characteristic maximum shifts to higher pseudoinversion values and the mean value < h_max(M’) > becomes 0.700.

The pseudoinversion histogram for the M-type sublettice changes more radically: the pronounced peak in the range of 0.3 - 0.4 in Figure 3(c) disappears in Figure 3(d), and the distribution becomes more uniform in a wider pseudoinversion range; the fraction of crystals with ultimately acentric M sublattices increases. The mean pseudo inversion < h_max(M) > becomes 0.384; i.e., it barely changes in comparison with < h_max(M) > for M sublattices without impurities. Thus, the analysis of the pseudo inversion of individual sublattices suggests that the reductions of pseudoinversion of structures as a whole at a transition to doped KTP compositions, which is noted in Table 2 and Figure 3(b), is related to a great extent to the higher sensitivity of the pseudoinversion of M-type sublattice to the presence of doped atoms. Note that pseudosymmetry was previously studied [58] by the atomic displacement method [1] for 11 KTP-type structures. In particular, it was established that the potassium sublattice is less centrosymmetric in comparison with the TiO₆-PO₄ subsystem, and its pseudosymmetry relative to inversion is more sensitive to introduction of impurities.

4. Comparison of the Nonlinear Optical Characteristics of KTP Crystals and the Pseudoinversion of Their Structures

A model was proposed in [8], according to which the second-order susceptibility of crystals is related to the symmetry of KTP-type structures and their pseudoinversion as follows:

(2)

As can be seen in Table 1, the SHG data with respect to the reference sample (powder of pure SiO₂ crystal) differ by an order of magnitude in different studies for KTP [3,5-7], and KTA [3,6,7] crystals. Based on this fact, we illustrated equation (2) by selecting a group of com-

Table 2. Maximum pseudoinversion values h_max and z coordinates of pseudoinversion centres z(h_max) for a number of KTP structures.

Figure 3. Distribution histogram of the degree of pseudoinversion for (a) pure KTP crystals (29 structures), (b) doped KTP crystals (89 structures), (c) pure atomic sublattices of individual types for 118 KTP crystals from Table 2, and (d) doped sublattices of individual types of atoms for 89 KTP crystals from Table 2.

positions (from the aforementioned set of crystals) for which experimental SHG data were obtained either by the powder method [26], or directly with respect to a powder of pure KTiOPO₄ crystal, or the data can be recalculated with respect to it based on a specific publication. In addition, since most sources yield data on the ratio of second-harmonic intensities for the studied and reference samples (I/I_KTP = I_2w/I_2w(KTP)), they were additionally recalculated into estimated values of the relative effective second-order susceptibility (it will be denoted as c_2w/c_2w(KTP)). In the first approximation, one can assume that where I_2w is the second harmonic intensity and I_w is the primary radiation intensity. Therefore, the desired ratio c_2w/c_2w(KTP) was estimated to be

.

Figure 4 shows the dependence of the set of c_2w/c_2w (KTP) values for KTiOPO₄ (CSD-№ 20970), RbTiOPO₄ (CSD-№ 281379, [10, 11]), KTiOAsO₄ (CSD-№ 202158, [14, 15]), K_0.565Li_0.34TiOPO₄ (CSD-№ 83482, [14]), RbTi_0.927Nb_0.056Er_0.017OPO₄ (CSD-№ 96408, [11]), Rb_0.855Ti_0.955Nb_0.045OPO₄ ([11]), K_0.534Li_0.34TiOAsO₄ (CSD-№ 83483, [14]), Na_0.87K_0.13TiOAsO₄ (CSD-№ 67541, [14]), K_0.89Nb_0.11Ti_0.89OPO₄ (CSD-№ 250046, [8]), K_0.96Nb_0.04Ti_0.96OPO₄ (CSD-№ 91556, [8]), K_0.99Ti_0.988Sb_0.0125OPO₄ (CSD-№ 250298, [8]), K_0.874Ti_0.927Sb_0.074OPO₄ (CSD-№ 250299, [8]), K_0.893Ti_0.833Sb_0.166OPO₄ (CSD-№ 250300, [8]), KTi_0.97Zr_0.03OPO₄ (CSD-№ 173235, [8]), and KTi_0.96Zr_0.04OPO₄ (CSD-№ 173233, [8]) crystals on the pseudoinversion h = h_max of their atomic structures in the coordinates. The linear approximation of the dependence presented in Figure 4 within the model described in [8], is characterized by a correlation coefficient of 0.91, and the confidence interval boundaries are (0.76, 0.97) at a confidence probability of 0.95.

Equation (2) can be more pronounced within the concentration series of samples of the same qualitative composition. For example, the SHG intensity decreases with an increase in the tin fraction in the KTi_1-xSn_xOPO₄ series, and the calculation of pseudoinversion for a series of known structures of this composition indicates a monotonic increase in the latter (Figure 5).

The boundary-composition crystal KSnOPO₄ has almost zero SHG intensity and the largest (in the KTi_1-xSn_xOPO₄ series) pseudoinversion: 0.886 (Table 1, no. 7; Table 2, no. 4). This fact is in agreement with the

Figure 4. Correlation between the relative effective secondorder susceptibility c2w/c2w(KTP) for a number of KTP crystals and their pseudoinversion in the coordinates (see [8] for the approximation model).

Figure 5. Dependence of the pseudoinversion on the tin content in KTi1-xSnxOPO4 crystals (calculation based on the structural data CSD-№ 20970, 91534, 72720, 250087, 250088, 68706).

data of Godfrey et al. [58], who established that the KSnOPO₄ structure can be partially described (in good approximation) by the Pnan group; exact description is obtained within the Pna2₁ group.

5. Conclusions

To date, despite the numerous publications on the structure and properties of KTP crystals, the question of the structural conditionality of the behavior of their nonlinear optical properties has not been completely clarified.

In this paper, we reported the results of studying the pseudosymmetric features of known structures of KTP crystals with respect to inversion and tried to analyze the entire set of known nonlinear optical parameters of these crystals in view of the obtained pseudosymmetric characteristics. In particular, it was shown that doped structures of KTP crystals have on average a lower degree of pseudoinversion than “pure” compositions; in some cases this feature adequately correlates with the increase in the relative intensity of the second optical harmonic. This correlation may manifest itself within the concentration series samples of the same qualitative composition.

We believe that, in order to establish the fundamental correlations between the structural and symmetric features of crystals (in particular, those belonging to the KTP family) and their nonlinear optical properties, for example, having the degree of pseudoinversion as a symmetric characteristic, it is necessary to primarily calculate this characteristic for the entire structure. This thesis is justified by the fundamental principles of symmetry in physical crystallography. The Neumann princeple, which sets a relationship between the symmetry of a medium (crystal) and the set of physical properties that are forbidden or allowed in this medium, deals with specifically the symmetry of the medium as a whole rather than the symmetry of its individual structural fragments within the unit cell. This approach was applied both in [8] and in this study. However, this does not depreciate the validity of the analysis of the characteristics of sublattices of individual types of atoms. Due to this analysis one can find sublattices with pseudosymmetric characteristics exhibiting a more significant sensitivity, for example, at a transition to doped compositions, and therefore, can determine to greater extent the behavior of the pseudosymmetric characteristics of crystal structures, as whole and physical properties of crystals.

6. Acknowledgements

This work was supported financially by the Ministry of Education and Science of the Russian Federation, project 14.B37.21.1158.

NOTES

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	C. Lee and E. V. Chuprunov, “Fedorov Pseudosymmetry of Crystals: Review,” Crystallography Reports, Vol. 52, No. 1, 2007, pp. 1-11. doi:10.1134/S1063774507010014
[2]	E. V. Chuprunov and E. A. Soldatov and T. N. Tarkhova, “The Quantitative Estimation of the Symmetry of the Crystal Structures,” Kristallografiya, Vol. 33, No. 3, 1988, pp. 759-761.
[3]	G. D. Stucky, M. L. F. Phillips and T. E. Gier, “The Potassium Titanyl Phosphate Structure Field: A Model for New Nonlinear Optical Materials,” Chemistry of Materials, Vol. 1, No. 5, 1989, pp. 492-509. doi:10.1021/cm00005a008
[4]	N. I. Sorokina and V. I. Voronkova, “Structure and Properties of Crystals in the Potassium Titanyl Phosphate Family: A Review,” Crystallography Reports, Vol. 52, No. 1, 2007, pp. 80-93. doi:10.1134/S1063774507010099
[5]	M. L. F. Phillips, T. E. Gier, M. M. Eddy, N. L. Keder and G. D. Stucky, “Inclusion Tuning of Nonlinear Optical Materials: KTP Isomorphs,” Solid State Ionics, Vol. 32-33, Part 1, 1989, pp. 147-153. doi:10.1016/0167-2738(89)90215-4
[6]	M. L. F. Phillips, W. T. A. Harrison and G. D. Stucky, “Nonlinear Optical Properties of New KTiOPO4 Isostructures,” SPIE Inorganic Crystals for Optics, Electro-Optics, and Frequency Conversion, Vol. 1561, 1991, pp. 84-92.
[7]	M. L. F. Phillips, W. T. A. Harrison, G. D. Stucky, E. M. McCarron, J. C. Calabrese and T. E. Gier, “Effects of Substitution Chemistry in the Potassium Titanyl Phosphate (KTiOPO4) Structure Field,” Chemistry of Materials, Vol. 4, No. 1, 1992, pp. 222-233. doi:10.1021/cm00019a041
[8]	V. A. Ivanov, V. A. Burdov, M. O. Marychev, D. N. Titaev, M. A. Faddeev and E. V. Chuprunov, “On the Effect of Structural and Symmetrical Features of Potassium Titanyl Phosphate Crystals with Different Contents of Niobium, Antimony, and Zirconium on the Second-Harmonic Intensity,” Crystallography Reports, Vol. 53, No. 4, 2008, pp. 678-682. doi:10.1134/S1063774508040202
[9]	D. N. Nikogosyan, “Nonlinear Optical Crystals: A Complete Survey,” Springer Science+Business Media, USA, 2005. doi:10.1007/b138685
[10]	J. J. Carvajal, V. Nikolov, R. Sole, J. Gavalda, J. Massons, M.Rico, C. Zaldo, M. Aguilo and F. Díaz, “Enhancement of the Erbium Concentration in RbTiOPO4 by Codoping with Niobium,” Chemistry of Materials, Vol. 12, No. 10, 2000, pp. 3171-3180. doi:10.1021/cm000305c
[11]	J. J. Carvajal, J. L. Garcia-Mun, R. Sole, J. Gavalda, J. Massons, X. Solans, F. Díaz and M. Aguilo, “Charge Self-Compensation in the Nonlinear Optical Crystals Rb0.855Ti0.955Nb0.045OPO4 and RbTi0.927Nb0.056Er0.017OPO4,” Chemistry of Materials , Vol. 1, No. 10, 2003, pp. 2338-2345. doi:/10.1021/cm034044t
[12]	M. M. Eddy, T. E. Gier, N. L. Keder, G. D. Stucky, D. E. Cox, J. D. Bierlein and G. Jones, “Inclusion Tuning of Nonlinear Optical Materials: Sorbates on the KTP Structure,” Inorganic Chemistry, 1988. Vol. 27, No. 11, 1988, pp. 1856-1858. doi:10.1021/ic00284a009
[13]	M. L. F. Phillips, W. T. A. Harrison and G. D. Stucky, “Influence of Electronic Configuration on the Structure and Optical Properties of Potassium Tin Oxide Phosphate,” Inorganic Chemistry, Vol. 29, No. 17, 1990, pp. 3245-3247. doi:10.1021/ic00342a040
[14]	M. E. Hagerman and K. R. Poeppelmeier, “Review of the Structure and Processing-Defect-Property Relationships of Potassium Titanyl Phosphate: A Strategy for Novel Thin-Film Photonic Devices,” Chemistry of Materials, Vol. 7, No. 4, 1995, pp. 602-621. doi:10.1021/cm00052a004
[15]	K. K. Rangan, B. R. Prasad, C. K. Subramanian and J. Gopalakrishnan, “Coupled Substitution of Niobium and Silicon in Potassium Titanyl Phosphate and Arsenate (KTiOPO4 and KTiOAsO4. Synthesis and Nonlinear Optical Properties of KTi1-xNbxOX1-xSixO4 (X = P, As),” Inorganic Chemistry, Vol. 32, No. 20, 1993, pp. 4291-4293. doi:10.1021/ic00072a022
[16]	L. K. Cheng, L. T. Cheng, J. D. Bierlein and F. C. Zumsteg, “Properties of Doped and Undoped Crystals of Single Domain KTiOAsO4,” Applied Physics Letters, Vol. 62, No. 4, 1993, pp 346-348. doi:10.1063/1.108953
[17]	L. T. Cheng, L. K. Cheng, J. D. Bierlein and F. C. Zumsteg, “Nonlinear Optical and Electro—Optical Properties of Single Crystal CsTiOAsO4,” Applied Physics Letters, Vol. 63, No. 19, 1993, pp. 2618-2620. doi:10.1063/1.110424
[18]	B. V. Mill’, A. V. Butashin and S. Yu. Stefanovich, “New Compounds with KTiOPO4-NaSbOGeO4, AgSbOGeO4 and AgSbOSiO4 Structure,” Zhurnal Neorganicheskoi Khimii, Vol. 38, No. 6, 1993, pp. 947-949.
[19]	W. T. A. Harrison and M. L. F. Phillips, “Syntheses, Structures, and Properties of RbScFAsO4 and CsScFAsO4: Scandium-Containing Analogues of Potassium Titanyl Phosphate (KTiOPO4),” Chemistry of Materials, Vol. 11, No. 12, 1999, pp. 3555-3560. doi:10.1021/cm990335j
[20]	F. C. Zumsteg, J. D. Bierlein and T. E. Gier, “KxRb1-x-TiOPO4: A New Nonlinear Optical Material,” Journal of Applied Physics, Vol. 47, No. 11, 1976, pp. 4980-4985. doi:10.1063/1.322459
[21]	V. I. Chani, K. Shimamura, S. Endo and T. Fukuda, “Growth of Mixed Crystals of the KTiOPO4 (KTP) Family,” Journal of Crystal Growth, Vol. 171, No. 3-4, 1997, pp. 472-476. doi:10.1016/S0022-0248(96)00693-8
[22]	M. L. F. Phillips, W. T. A. Harrison, T. E. Giers, G. D. Stucky, G. V. Kulkarni, J. K. Burdett, “Electronic Effects of Substitution Chemistry in the Potassium Titanyl Phosphate (KTiOPO4) Structure Field: Structure and Optical Properties of Potassium Vanadyl Phosphate,” Inorganic Chemistry, Vol. 29, No. 11, 1990, pp. 2158-2163. doi:10.1021/ic00336a024
[23]	J. Gopalakrishnan, K. K. Rangan, B. R. Prasad and C. K. Subramanian, “New Transition Metal Phosphates Related to KTiOPO4. Synthesis of K0.5M0.5M’0.5OPO4 (M = Nb, Ta; M’ = Ti, V) and K1-xTi1-xVxOPO4 Exhibiting Nonlinear Optical Behavior,” Journal of Solid State Chemistry, Vol. 111, No. 1, 1994, pp. 41-47. doi:10.1006/jssc.1994.1196
[24]	A. Pena, J. J. Carvajal, J. Massons, Jna. Gavaldà, F. Dlaz and M. Aguiló, “Yb: Ta:RbTiOPO4, A New Strategy to Further Increase the Lanthanide Concentration in Crystals of the KTiOPO4 Family,” Chemistry of Materials, Vol. 19, No. 16, 2007, pp. 4069-4076. doi:/10.1021/cm070887z
[25]	T. Hikita, “35B-1 (A, B)(C, D)OPO4 (A, B = H, NH4, Na, K, Rb, Ag, Cs, Tl; C, D = Ti, V, Nb),” In: Y. Shiozaki, E. Nakamura, T. Mitsui Eds., SpringerMaterials—The Landolt-Bornstein Database, Vol. 36B1, 2004, pp 1-28, 9e. doi:10.1007/10635019_143
[26]	S. K. Kurtz and T. T. Perry, “A Powder Technique for the Evaluation of Nonlinear Optical Materials,” Journal of Applied Physics, 1968. Vol. 39, No. 8, 1968, pp. 3798-3813. doi:10.1063/1.1656857
[27]	J. P. Dougherty and S. K. L. Kurtz, “A Second Harmonic Analyzer for the Detection of Non-Centrosymmetry,” Journal of Applied Crystallography, Vol. 9, Part 2, 1976, pp. 145-158. doi:10.1107/S0021889876010789
[28]	P. D. Maker, R. W. Terhune, M. Nisenoff and C. M. Savage, “Effects of Dispersion and Focusing on the Production of Optical Harmonics,” Physical Review Letters, Vol. 8, No. 1, 1962, pp. 21-22. doi:10.1103/PhysRevLett.8.21
[29]	J. Jerphagnon and S. K. Kurtz, “Optical Nonlinear Susceptibilities: Accurate Relative Values for Quartz, Ammonium Dihydrogen Phosphate, and Potassium Dihydrogen Phosphate,” Physical Review B, Vol. 1, No. 4, 1970, pp. 1739-1744. doi:10.1103/PhysRevB.1.1739
[30]	P. A. Thomas and B. E. Watts, “An Nb-doped Analogue of KTiOPO4; Structural and Nonlinear Optical Properties,” Solid State Communications, Vol. 73, No. 2, 1990, pp. 97-100. doi:10.1016/0038-1098(90)91025-C
[31]	T. Yu. Losevskaya, O. A. Alekseeva, V. K. Yanovskii, V. I. Voronkova, N. I. Sorokina, V. I. Simonov, S. Yu. Stefanovich, S. A. Ivanov, S. Eriksson and S. A. Zverkov, “Structure and Properties of Niobium-Doped Potassium Titanyl Phosphate Crystals,” Crystallography Reports, Vol. 45, No. 5, 2000, pp. 739-743. doi:10.1134/1.1312912
[32]	O. A. Alekseeva, M. K. Blomberg, V. N. Molchanov, I. A. Verin, N. I. Sorokina, T. Yu. Losevskaya, V. I. Voronkova and V. K. Yanovskii, “Refinement of the K0.96Ti0.96Nb0.04OPO4 Structure,” Crystallography Reports, Vol. 46, No. 4, 2001, pp. 642-646. doi:10.1134/1.1387131
[33]	V. K. Yanovski, V. I. Voronkova, T. Yu. Losevskaya, S. Yu. Stefanovich, S. A. Ivanov, V. I. Simonov and N. I. Sorokina, “Growth and Properties of Nb-or Sn-Doped KTiOPO4 Crystals,” Crystallography Reports, Vol. 47, Suppl. 1, 2002, pp. S99-S104. doi:10.1134/1.1529963
[34]	O. A. Alekseeva, N. I. Sorokina, I. A. Verin, T. Yu. Losevskaya, V. I. Voronkova, V. K. Yanovskii and V. I. Simonov, “Structure and Properties of Potassium Titanyl Phosphate Single Crystals with 7 and 11 at. % Nb,” Crystallography Reports, Vol. 48, No. 2, 2003, pp. 205-211. doi:10.1134/1.1564196
[35]	V. I. Voronkova, V. K. Yanovskii, T. Yu. Losevskaya, S. Yu. Stefanovich, S. A. Zver’kov, O. A. Alekseeva and N. I. Sorokina, “Electrical and Nonlinear Optical Properties of KTiOPO4 Single Crystals Doped with Niobium, Antimony, and Tantalum,” Crystallography Reports, Vol. 49, No. 1, 2004, pp. 123-129. doi:10.1134/1.1643973
[36]	A. P. Dudka, I. A. Verin, V. N. Molchanov, M. K. Blomberg, O. A. Alekseeva, N. I. Sorokina, N. E. Novikova and V. I. Simonov, “Structural Study of K0.93Ti0.93Nb0.07OPO4 Single Crystals at 30 K,” Crystallography Reports, Vol. 50, No. 1, 2005, pp. 36-41. doi:10.1134/1.1857242
[37]	N. I. Sorokina, V. I. Voronkova, V. K. Yanovskii, I. A. Verin and V. I. Simonov, “Crystal Structures of Compounds in the KTiOPO4-KGeOPO4 System,” Crystallography Reports, Vol. 41, No. 3, 1996, pp. 435-435.
[38]	L. Wen, N. I. Sorokina, V. I. Voronkova, V. K. Yanovskii, I. A. Verin, A. G. Vigdorchik and V. I. Simonov, “Crystal Structure of KTi0.93Sn0.07OPO4,” Crystallography Reports, Vol. 45, No. 3, 2000, pp. 386-388. doi:10.1134/1.171203
[39]	L. Wen, V. I. Voronkova, V. K. Yanovskii, S. Y. Stefanovich, N. I. Sorokina and I. A. Verin, “Growth and Properties of KTi1-xSnxOPO4 Crystals,” Inorganic Materials, Vol. 37, No. 3, 2001, pp. 290-293. doi:10.1023/A:1004129817488
[40]	O. D. Krotova, N. I. Sorokina, I. A. Verin, V. I. Voronkova, V. K. Yanovskii and V. I. Simonov, “Structure and Properties of Single Crystals of Tin-Doped Potassium Titanyl Phosphate,” Crystallography Reports, Vol. 48, No. 6, 2003, pp. 925-932. doi:10.1134/1.1627433
[41]	V. I. Voronkova, V. K. Yanovskii, I. N. Leont’eva, E. I. Agapova, E. P. Kharitonova, S. Y. Stefanovich and S. A. Zver’kov, “Growth and Properties of Zr-Doped KTiOPO4 Crystals,” Inorganic Materials, Vol. 40, No. 12, 2004, pp. 1321-1323. doi:10.1007/s10789-005-0018-z
[42]	O. A. Alekseeva, A. P. Dudka, N. I. Sorokina, A. Pietraszko, M. Kh. Rabadanov, E. I. Agapova, V. I. Voronkova and V. I. Simonov, “Crystal Structure of Potassium Titanyl Phosphate Doped with Zirconium,” Crystallography Reports, Vol. 52, No. 4, 2007, pp. 659-667. doi:10.1134/S106377450704013X
[43]	N. E. Novikova, I. A. Verin, N. I. Sorokina, O. A. Alekseeva, E. I. Agapova and V. I. Voronkova, “Structural Reasons for the Nonlinear Optical Properties of KTi0.96Zr0.04OPO4 Single Crystals,” Crystallography Reports, Vol. 54, No. 2, 2009, pp. 219-227. doi:10.1134/S1063774509020096
[44]	O. A. Alekseeva, O. D. Krotova, N. I. Sorokina, I. A. Verin, T. Y. Losevskaya, V. I. Voronkova, V. K. Yanovskii and V. I. Simonov, “Structure and Properties of Antimony-Doped Potassium Titanyl Phosphate Single Crystals,” Crystallography Reports, Vol. 50, No. 4, 2005, pp. 554-565.
[45]	V. V. Atuchin, O. A. Alekseeva, V. G. Kesler, L. D. Pokrovsky, N. I. Sorokina and V. I. Voronkova, “Chemical Shifts of Atomic Core Levels and Structure of K1-xTi1-xSbxOPO4, x=0-0.23, Solid Solutions,” Journal of Solid State Chemistry, Vol. 179, No. 8, 2006, pp. 2349-2355. doi:10.1016/j.jssc.2006.04.025
[46]	V. I. Voronkova, I. N. Leont’eva, N. I. Sorokina, T. I. Ovsetsina and I. A. Verin, “Growth, Structure, and Properties of KTiOPO4 Crystals Doped with Iron,” Crystallography Reports, Vol. 51, No. 6, 2006, pp. 977-981. doi:10.1134/S1063774506060071
[47]	E. I. Orlova, E. P. Kharitonova, N. E. Novikova, I. A. Verin, O. A. Alekseeva, N. I. Sorokina and V. I. Voronkova, “Synthesis, Properties, and Structure of Potassium Titanyl Phosphate Single Crystals Doped with Hafnium,” Crystallography Reports, Vol. 55, No. 3, 2010, pp. 404-411. doi:10.1134/S1063774510030077
[48]	E. I. Orlova, N. E. Novikova, A. Gagor, I. A. Verin, A. Pietraszko, D. A. Belov and V. I. Voronkova, “Growth of KTiOPO4 Crystals Doped with Zinc and Studies of Their Physical Properties and Specific Structural Features,” Crystallography Reports, Vol. 55, No. 4, 2010, pp. 594-601. doi:10.1134/S1063774510040103
[49]	L. Wen, V. I. Voronkova, V. K. Yanovskii, N. I. Sorokina, I. A. Verin and V. I. Simonov, “Synthesis, Atomic Structure, and Properties of Crystals in the RbTiOPO4-CsTiPO5 System,” Crystallography Reports, Vol. 45, No. 3, 2000, pp. 380-385. doi:10.1134/1.171202
[50]	E. I. Agapova, V. I. Voronkova, E. P. Kharitonova, I. N. Leont’eva, S. Y. Stefanovich, N. I. Sorokina, A. P. Dudka, O. A. Alekseeva and N. N. Kononkova, “Synthesis and Properties of Zirconium-Doped RbTiOPO4 Single Crystals,” Crystallography Reports, Vol. 53, No. 2, 2008, pp. 285-290. doi:10.1134/S1063774508020181
[51]	O. A. Alekseeva, A. P. Dudka, N. E. Novikova, N. I. Sorokina, E. I. Agapova and V. I. Voronkova, “Structure of the RbTi0.98Zr0.02OPO4 Single Crystal at Temperatures of 293 and 105 K,” Crystallography Reports, Vol. 53, No. 4, 2008, pp. 557-564. doi:10.1134/S1063774508040056
[52]	A. R. Pena, “Ytterbium and Erbium Doped RbTi1-xMxOPO4 (M=Nb or Ta) Crystals. New Laser and Nonlinear Bifunctional Materials,” Doctoral Thesis, Física I Cristallografia de Materials (FiCMA), Tarragona, 2007. http://www.tesisenred.net/handle/10803/9087
[53]	M. T. Anderson, M. L. F. Phillips, M. B. Sinclair and G. D. Stucky, “Synthesis of Transition-Metal-Doped KTiOPO4 and Lanthanide-Doped RbTiOAsO4 Isomorphs that Absorb Visible Light,” Chemistry of Materials, Vol. 8, No. 1, 1996, pp. 248-256. doi:10.1021/cm950352i
[54]	N. V. Somov and E. V. Chuprunov, “Pseudosymmetry of Atomic Crystal Structures,” In: E. V. Chuprunov, Ed., Crystallography: Laboratory Workshop, Fizmatlit, Moskow, 2005, pp. 80-90.
[55]	T. Hahn, “International Tables for Crystallography. Vol. A: Space-Group Symmetry,” Springer, Berlin, 2005. doi:10.1107/97809553602060000100
[56]	Inorganic Crystal Structure Data-base. Version 2010-1. http://www.fiz-karlsruhe.de/icsd.html/
[57]	T. Nakagawa, T. Matsumoto, V. I. Chani and T. Fukuda, “K2NbAlO2[(As,Nb)O4]2, Isostructural with KTiOPO4,” Acta Crystallographica Section C, Vol. 55, 1999, pp. 1391-1393. doi:10.1107/S0108270199005144
[58]	K. W. Godfrey, P. A. Thomas and B. E. Watts, “The Structural and Optical Properties of Potassium Titanyl Phosphate and Its Analogues,” Materials Science and Engineering B, Vol. 9, No. 4, 1991, pp. 479-483.