1. Introduction
We can fix some Riemannian metric g on a manifold Mn of dimension n which defines the length of arc of a piecewise smooth curve and the continuous function 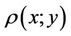 of the distance between two points
of the distance between two points . The topology defined by the function of distance (metric)
. The topology defined by the function of distance (metric)  is the same as the topology of the manifold Mn [1].
is the same as the topology of the manifold Mn [1].
In Section 1, using a smooth triangulation considered in the main theorem and a Riemannian metric we construct an algorithm of extension of coordinate neighborhood. With the help of this algorithm we get that every compact, connected, closed manifold Mn of dimension n having the triangulation above can be represented as a union of a n-dimensional cell Cn and a connected union 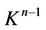 of some finite number of simplexes of the triangulation having dimension less or equal
of some finite number of simplexes of the triangulation having dimension less or equal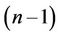 . A sufficiently small closed neighborhood of
. A sufficiently small closed neighborhood of  is called a geometric black hole [2]. Simplexes with boundaries can be retracted i.e. a decomposition
is called a geometric black hole [2]. Simplexes with boundaries can be retracted i.e. a decomposition 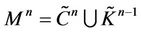 can be obtained where
can be obtained where  contains less simplexes than
contains less simplexes than 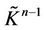 does.
does.
In Section 2, we consider the proof of the main theorem consisting of the realization of several algorithms. Using the method of mathematical induction and the algorithms we retract all the simplexes from 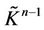 to a point x0, therefore a decomposition
to a point x0, therefore a decomposition  is obtained and Mn is homeomorphic to the sphere
is obtained and Mn is homeomorphic to the sphere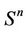 .
.
2. On Algorithm of Extension of Coordinate Neighborhood
1) Let Mn be a connected, compact, closed and smooth manifold of dimension n and Cn be a cell (coordinate neighborhood) on Mn. A standard simplex ∆n of dimension n is the set of points  defined by conditions
defined by conditions

We consider the interval of a straight line connected the center of some face of ∆n and the vertex which is opposite to this face. It is clear that the center of ∆n belongs to the interval. We can decompose ∆n as a set of intervals which are parallel to that mentioned above. If the center of ∆n is connected by intervals with points of some face of ∆n then a subsimplex of ∆n is obtained. All the faces of ∆n considered, ∆n is seen as a set of all such subsimplexes. Let  be some open neighborhood of ∆n in Rn. A diffeomorphism
be some open neighborhood of ∆n in Rn. A diffeomorphism 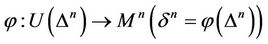 is called a singular nsimplex on the manifold Mn. Faces, edges, the center, vertexes of the simplex
is called a singular nsimplex on the manifold Mn. Faces, edges, the center, vertexes of the simplex  are defined as the images of those of ∆n with respect to
are defined as the images of those of ∆n with respect to .
.
The manifold Mn is triangulable [3]. It means that for any  such a finite set
such a finite set 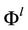 of diffeomorphisms
of diffeomorphisms  is defined that
is defined that
a) Mn is a disjunct union of images ;
;
b) if  then
then  for every i where
for every i where  is the linear mapping transferring the vertexes
is the linear mapping transferring the vertexes  of the simplex
of the simplex  in the vertexes
in the vertexes 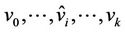 of the simplex
of the simplex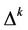 .
.
We suppose that there exists a smooth finite triangulation on Mn which is coordinated with the smoothness structure of Mn and fix the triangulation. Such triangulations exist for manifolds of dimension 2 or 3.
2) Let 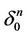 be some simplex of the fixed triangulation of the manifold Mn. We paint the inner part
be some simplex of the fixed triangulation of the manifold Mn. We paint the inner part 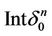 of the simplex
of the simplex 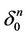 white and the boundary
white and the boundary 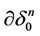 of
of 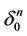 black. There exist coordinates on
black. There exist coordinates on 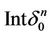 given by diffeomorphism
given by diffeomorphism . A subsimplex
. A subsimplex 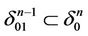 is defined by a black face
is defined by a black face 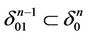 and the center
and the center 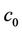 of
of . We connect
. We connect 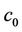 with the center
with the center 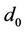 of the face
of the face  and decompose the subsimplex
and decompose the subsimplex 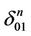 as a set of intervals which are parallel to the interval
as a set of intervals which are parallel to the interval . The face
. The face  is a face of some simplex
is a face of some simplex  that has not been painted. We draw an interval between
that has not been painted. We draw an interval between  and the vertex
and the vertex  of the subsimplex
of the subsimplex 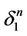 which is opposite to the face
which is opposite to the face 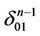 then we decompose
then we decompose 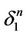 as a set of intervals which are parallel to the interval
as a set of intervals which are parallel to the interval . The set
. The set 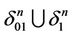 is a union of such broken lines every one from which consists of two intervals where the endpoint of the first interval coincides with the beginning of the second interval (in the face
is a union of such broken lines every one from which consists of two intervals where the endpoint of the first interval coincides with the beginning of the second interval (in the face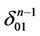 ) the first interval belongs to
) the first interval belongs to 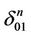 and the second interval belongs to
and the second interval belongs to . We construct a homeomorphism (extension)
. We construct a homeomorphism (extension) :
: . Let us consider a point
. Let us consider a point 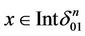 and let x belong to a broken line consisting of two intervals the first interval is of a length of
and let x belong to a broken line consisting of two intervals the first interval is of a length of 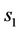 and the second interval is of a length of
and the second interval is of a length of  and let x be at a distance of s from the beginning of the first interval. Then we suppose that
and let x be at a distance of s from the beginning of the first interval. Then we suppose that 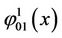 belongs to the same broken line at a distance of
belongs to the same broken line at a distance of 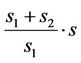 from the beginning of the first interval. It is clear that
from the beginning of the first interval. It is clear that  is a homeomorphism giving coordinates on
is a homeomorphism giving coordinates on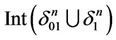 . We paint points of
. We paint points of  white. Assuming the coordinates of points of white initial faces of subsimplex
white. Assuming the coordinates of points of white initial faces of subsimplex 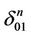 to be fixed we obtain correctly introduced coordinates on
to be fixed we obtain correctly introduced coordinates on . The set
. The set  is called a canonical polyhedron. We paint faces of the boundary
is called a canonical polyhedron. We paint faces of the boundary 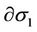 black.
black.
We describe the contents of the successive step of the algorithm of extension of coordinate neighborhood. Let us have a canonical polyhedron 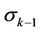 with white inner points (they have introduced white coordinates) and the black boundary
with white inner points (they have introduced white coordinates) and the black boundary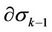 . We look for such an n-simplex in
. We look for such an n-simplex in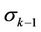 , let it be
, let it be 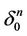 that has such a black face, let it be
that has such a black face, let it be 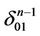 that is simultaneously a face of some n-simplex, let it be
that is simultaneously a face of some n-simplex, let it be , inner points of which are not painted. Then we apply the procedure described above to the pair
, inner points of which are not painted. Then we apply the procedure described above to the pair ,
, . As a result we have a polyhedron
. As a result we have a polyhedron 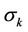 with one simplex more than
with one simplex more than  has. Points of
has. Points of  are painted white and the boundary
are painted white and the boundary  is painted black. The process is finished in the case when all the black faces of the last polyhedron border on the set of white points (the cell) from two sides.
is painted black. The process is finished in the case when all the black faces of the last polyhedron border on the set of white points (the cell) from two sides.
After that all the points of the manifold 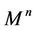 are painted in black or white, otherwise we would have that
are painted in black or white, otherwise we would have that 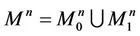 (the points of
(the points of 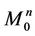 would be painted and those of
would be painted and those of  would be not) with
would be not) with 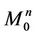 and
and  being unconnected, which would contradict of connectivity of
being unconnected, which would contradict of connectivity of .
.
Thus, we have proved the following.
Theorem 1. Let 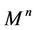 be a connected, compact, closed, smooth manifold of dimension n. Then
be a connected, compact, closed, smooth manifold of dimension n. Then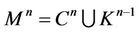 ,
, 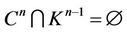 , where
, where 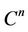 is an п-dimensional cell and
is an п-dimensional cell and 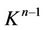 is a union of some finite number of
is a union of some finite number of  -simplexes of the triangulation.
-simplexes of the triangulation.
3) We consider the initial simplex 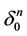 of the triangulation and its center
of the triangulation and its center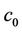 . Drawing intervals between the point
. Drawing intervals between the point 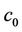 and points of all the faces of
and points of all the faces of  we obtain a decomposition of
we obtain a decomposition of 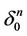 as a set of the intervals. In 2) the homeomorphism
as a set of the intervals. In 2) the homeomorphism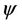 :
:  was constructed and
was constructed and 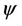 evidently maps every interval above on a piecewise smooth broken line
evidently maps every interval above on a piecewise smooth broken line 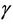 in Cn. We denote
in Cn. We denote .
.  is a connected and simply connected manifold if
is a connected and simply connected manifold if  is that. Let
is that. Let , we define a homotopy
, we define a homotopy  in the following way
in the following way
a)  for every point
for every point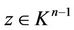 ;
;
b) if a point x belongs to the broken line 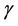 in
in 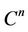 and the distance between x and its limit point
and the distance between x and its limit point  is
is 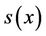 then
then  is on the same broken line
is on the same broken line 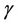 at a distance of
at a distance of  from the point z.
from the point z.
It is clear that ,
, 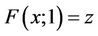 and we have obtained the following.
and we have obtained the following.
Theorem 2. The spaces  and
and  are homotopyequivalent, in particular, the groups of singular homologies
are homotopyequivalent, in particular, the groups of singular homologies 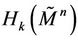 and
and 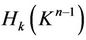 are isomorphic for every k.
are isomorphic for every k.
Corollary 2.1. The space 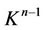 is connected and if Mn is simply connected then
is connected and if Mn is simply connected then  is simply connected too.
is simply connected too.
Remark 1. The white coordinates are extended from the simplex  in the simplex
in the simplex  through the face
through the face  hence
hence 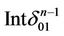 has also the white coordinates. On the other hand there exist two linear structures (intervals, the center etc.) on
has also the white coordinates. On the other hand there exist two linear structures (intervals, the center etc.) on 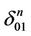 induced from
induced from  and
and 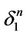 respectively. Further, we set that the linear structure of
respectively. Further, we set that the linear structure of 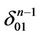 is the structure induced from
is the structure induced from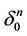 .
.
Remark 2. In the process of getting of  in 2) we can construct a maximal tree L connecting by intervals all the centers of the n-simplexes of the triangulation via the centers of some white faces.
in 2) we can construct a maximal tree L connecting by intervals all the centers of the n-simplexes of the triangulation via the centers of some white faces.
Conversely, if we have such a maximal tree L connecting by intervals all the centers of the n-simplexes of the triangulation via the centers of some faces (any from two possible centers of a face can be chosen) then we can extend white coordinates from any simplex 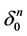 on the maximal cell Cn as it was shown in 2). Thus, the maximal tree L defines the maximal cell C3 and white faces.
on the maximal cell Cn as it was shown in 2). Thus, the maximal tree L defines the maximal cell C3 and white faces.
4) Definition 1.
a) A simplex  is called free if it has at least one free face
is called free if it has at least one free face 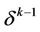 i.e. such a face that it is not a face of any other k-simplex from
i.e. such a face that it is not a face of any other k-simplex from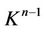 .
.
b) An edge 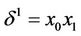 is called semi-isolated if it is not an edge of any simplex from
is called semi-isolated if it is not an edge of any simplex from . A semi-isolated edge
. A semi-isolated edge 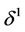 is called isolated if it is free.
is called isolated if it is free.
Let us have a free simplex 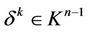 with some free face
with some free face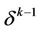 . We consider such a polyhedron
. We consider such a polyhedron 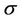 that
that 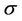 is the set of all n-simplexes having common point with
is the set of all n-simplexes having common point with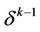 .
.
Proposition 3. We can redistribute coordinates of white points of the polyhedron  (retract the free simplex
(retract the free simplex ) i.e. construct the corresponding mapping
) i.e. construct the corresponding mapping 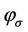 in such a way that the following conditions are fulfilled:
in such a way that the following conditions are fulfilled:
a) all the points of  are painted white i.e. have new white coordinatesb) white coordinates of points of boundary faces of the polyhedron
are painted white i.e. have new white coordinatesb) white coordinates of points of boundary faces of the polyhedron 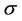 are not changed.
are not changed.
Proof. a) We consider the unit disk D2 having the center in the origin 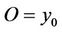 of the coordinate system
of the coordinate system 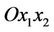 of
of  and the radius
and the radius .
.

We define a mapping  by the following way:
by the following way:
• 
• for any chord 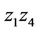 which is parallel to
which is parallel to 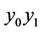

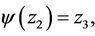
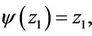
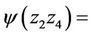
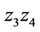 ,
, 
It is clear that 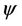 maps
maps  onto
onto 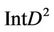 and
and  on the boundary circle of
on the boundary circle of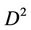 .
.
b) We consider the unit disk 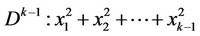
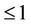 having the center in the origin
having the center in the origin 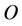 of the coordinate system
of the coordinate system 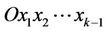 and the semidisk
and the semidisk ,
,  ,
, . By inductive hypothesis we assume that such a mapping
. By inductive hypothesis we assume that such a mapping  has been constructed that
has been constructed that  maps
maps 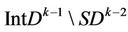 onto
onto  and
and  on the boundary of
on the boundary of .
.
Further, we consider the unit disk 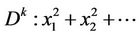
 in the coordinate system
in the coordinate system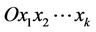 , the semidisk
, the semidisk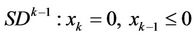 ,
, 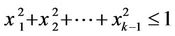 and the family of disks
and the family of disks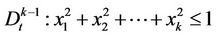 ,
, 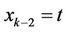 ,
,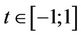 . We denote
. We denote  By inductive hypothesis there exists such the family of mappings
By inductive hypothesis there exists such the family of mappings 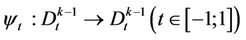 that every
that every 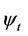 maps
maps 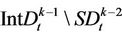 onto
onto  and
and 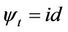 on the boundary of
on the boundary of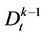 . Union of all
. Union of all  gives the mapping
gives the mapping ,
,  maps
maps 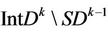 onto
onto 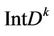 and
and  on the boundary of
on the boundary of .
.
Thus, the mapping  is constructed for any
is constructed for any 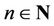 by the method of mathematical induction.
by the method of mathematical induction.
c) It is clear that there exists such a homeomorphism  that
that  and
and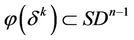 . We define the mapping
. We define the mapping 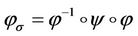 then
then 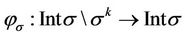 is a required homeomorphism introducing new white coordinates in
is a required homeomorphism introducing new white coordinates in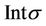 .
.
QED.
Remark 3. In is clear that the rebuilt complex 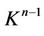 is connected and simply connected because of a homotopy-equivalence.
is connected and simply connected because of a homotopy-equivalence.
5) We assume that in the process of painting free simplexes white by the Proposition 3 we get a representation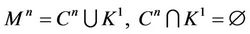 , where K1 is the connected union of black edges of the triangulation. Since the process of painting free simplexes white does not influence simply connectivity of a space that has been obtained every step then K1 is a tree if the complex
, where K1 is the connected union of black edges of the triangulation. Since the process of painting free simplexes white does not influence simply connectivity of a space that has been obtained every step then K1 is a tree if the complex 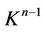 is simply connected. Painting isolated edges of K1 white by the Proposition 3 we have got unique black point x0 as result. Thus, we obtain a representation
is simply connected. Painting isolated edges of K1 white by the Proposition 3 we have got unique black point x0 as result. Thus, we obtain a representation , where
, where  is an open geodesic ball with the center in x0 and of a radius
is an open geodesic ball with the center in x0 and of a radius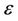 . The manifold Mn is homeomorfic to the sphere Sn by the following lemma 4.
. The manifold Mn is homeomorfic to the sphere Sn by the following lemma 4.
Lemma 4 [1]. If a topological manifold Mn is a union of two n-dimensional cells then Mn is homeomorfic to the sphere Sn.
3. Proof of the Main Theorem
The proof has a combinatorial nature and assumes the realization of a number of algorithms. We consider that step by step. The initial complex  is assumed to be connected, simply connected and without free simplexes.
is assumed to be connected, simply connected and without free simplexes.
1) Proposition 5 (opening an input). Let 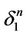 be some n–simplex of the triangulation having a black face
be some n–simplex of the triangulation having a black face . Then
. Then 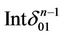 can be repainted white to get a new decomposition
can be repainted white to get a new decomposition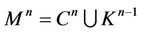 , where
, where  is a new connected and simply connected complex.
is a new connected and simply connected complex.
Proof. The face  is the common face of n-simplexes
is the common face of n-simplexes 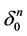 and
and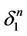 . We cansel the white painting of points of
. We cansel the white painting of points of  and paint the n-simplexe
and paint the n-simplexe  black. Repainting of
black. Repainting of  black brings to a gap of the maximal tree L (see the Remark 2) on n subtrees
black brings to a gap of the maximal tree L (see the Remark 2) on n subtrees 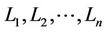 or less where the center of
or less where the center of 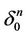 belongs to
belongs to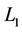 . Further, we extend white coordinates from
. Further, we extend white coordinates from  into
into  through the face
through the face 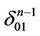 as it was shown in 2), 1 and connect the centers of
as it was shown in 2), 1 and connect the centers of ,
, 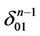 ,
, 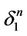 by intervals. Those centers belong to the subtree
by intervals. Those centers belong to the subtree . Other faces of
. Other faces of 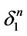 are black and they are simultaneously some faces of other n-simplexes.
are black and they are simultaneously some faces of other n-simplexes.
We consider the following cases.
a) 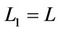 or we have no a gap. The black faces of
or we have no a gap. The black faces of  remain black.
remain black.
b) We have got k subtrees  where the subtrees
where the subtrees  define cells called dead ends. We repaint the closures of the dead ends black. Further, we are looking for a black face of
define cells called dead ends. We repaint the closures of the dead ends black. Further, we are looking for a black face of 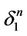 which is simultaneously a face of other n-simplex with the center from
which is simultaneously a face of other n-simplex with the center from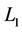 . This face remains black. For every subtree
. This face remains black. For every subtree 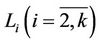 we consider a n-simplex with the center from
we consider a n-simplex with the center from  that has a common black face
that has a common black face 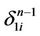 with
with . We extend white coordinates from
. We extend white coordinates from 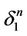 through
through  along the subtree
along the subtree 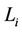 as it was shown in 2), 1 and repaint inner points of this face and points of the corresponding dead end white. Further, we connect by intervals the centers of
as it was shown in 2), 1 and repaint inner points of this face and points of the corresponding dead end white. Further, we connect by intervals the centers of 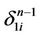 with the centers of
with the centers of  and the other simplex connecting
and the other simplex connecting  and
and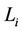 .
.
After repainting all the dead ends white we obtain a new maximal tree L defining a new maximal cell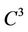 . Retracting all the free simplexes by the Proposition 3 a new rebuilt complex
. Retracting all the free simplexes by the Proposition 3 a new rebuilt complex 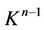 is obtained which is connected and simply connected because of homotopyequivalence.
is obtained which is connected and simply connected because of homotopyequivalence.
QED.
Remark 4. A broken line has been obtained in the proof above which connects by intervals the centers of ,
, 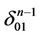 ,
,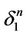 . This broken line is a part of the subtree
. This broken line is a part of the subtree  of the maximal tree L. Let n-simplexes
of the maximal tree L. Let n-simplexes  and
and  have a common face
have a common face 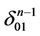 having the white inter part and
having the white inter part and 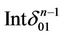 has no common points with the maximal tree
has no common points with the maximal tree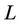 . Then we can connect the centers of
. Then we can connect the centers of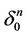 ,
, 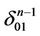 ,
,  by the broken line by the method considered in the proof above.
by the broken line by the method considered in the proof above.
2) We assume the following inductive hypothesis:
The generalized Poincare conjecture (the main theorem) can be proved by the method considered in [4] for dimension n–1 i.e. the representation  can be obtained by the algorithm from 2), 1 and by the Propositions 3, 4, 5.
can be obtained by the algorithm from 2), 1 and by the Propositions 3, 4, 5.
It is obvious for 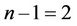 (see 5), 1) It is proved for
(see 5), 1) It is proved for  in [4].
in [4].
We choose a small ball  with the center in a vertex x0 which is diffeomorphic to a small ball in
with the center in a vertex x0 which is diffeomorphic to a small ball in 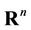 and call a trace of k-simplex
and call a trace of k-simplex  with a vertex in x0 its intersection
with a vertex in x0 its intersection 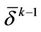 with the sphere
with the sphere  (smooth manifold) which is the boundary of
(smooth manifold) which is the boundary of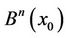 . The sphere
. The sphere  is supposed to be transversal to all the k-simplexes
is supposed to be transversal to all the k-simplexes  with the vertex x0. Such a sphere
with the vertex x0. Such a sphere  exists because of the smoothness of the triangulation of Mn [5,6]. All other vertexes of the triangulation are supposed to be out of
exists because of the smoothness of the triangulation of Mn [5,6]. All other vertexes of the triangulation are supposed to be out of . The ball
. The ball  can be chosen in such a vay that every edge with the endpoint x0 has only one point of the intersection with
can be chosen in such a vay that every edge with the endpoint x0 has only one point of the intersection with  and every k-simplex
and every k-simplex 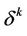 with the vertex x0 has only one connected component
with the vertex x0 has only one connected component  of
of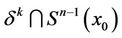 . Let
. Let 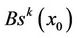 be the set of black k-simplexes with x0 as their vertex and
be the set of black k-simplexes with x0 as their vertex and .
.
There exists one to one correspondence between the set of simplexes having a vertex (endpoint) x0 and the set of their traces on 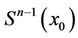 therefore all steps of the algorithm below bring to the corresponding steps on the sphere
therefore all steps of the algorithm below bring to the corresponding steps on the sphere  and the converse is true. In particular, a process of the construction of a maximal tree
and the converse is true. In particular, a process of the construction of a maximal tree 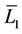 on the sphere
on the sphere  (see the Remark 2) brings to the construction of a tree L1 connecting by intervals all the centers of the n-simplexes with x0 as their vertex via the centers of some white their faces. Every such the face has x0 as its vertex.
(see the Remark 2) brings to the construction of a tree L1 connecting by intervals all the centers of the n-simplexes with x0 as their vertex via the centers of some white their faces. Every such the face has x0 as its vertex.
Proposition 6. The complex  can be rebuilt in such a vay that
can be rebuilt in such a vay that 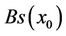 contains only one 1-simplex
contains only one 1-simplex .
.
Proof. We consider the smooth triangulation of  induced by all the simplexes with the vertex
induced by all the simplexes with the vertex  and apply to this triangulation the algorithm from 2), 1 taking any
and apply to this triangulation the algorithm from 2), 1 taking any 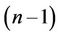 -simplex
-simplex  as initial one where
as initial one where 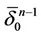 is the trace of
is the trace of 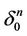 with a vertex
with a vertex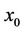 . Let
. Let  be the trace on
be the trace on  of
of  with a vertex x0 where
with a vertex x0 where 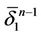 has a common face with
has a common face with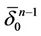 . We repaint
. We repaint 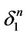 black and apply to it the proposition 5 (the remark 4) obtaining the canonical polyhedron
black and apply to it the proposition 5 (the remark 4) obtaining the canonical polyhedron  on
on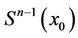 . Further, we iterate the algorithm. Every step of the algorithm on
. Further, we iterate the algorithm. Every step of the algorithm on 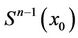 implies the transformation of
implies the transformation of 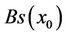 and
and 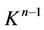 by the proposition 5 (the remark 4). The maximal tree
by the proposition 5 (the remark 4). The maximal tree  on
on 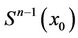 and the corresponding subtree
and the corresponding subtree 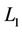 have been constructed in the end. Further, free black simplexes on
have been constructed in the end. Further, free black simplexes on 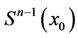 and the corresponding free simplexes from
and the corresponding free simplexes from  can be annihilated by the propositions 3, 4, 5. By the inductive hypothesis only one black point remains on
can be annihilated by the propositions 3, 4, 5. By the inductive hypothesis only one black point remains on  in the end. This point is the trace of an edge
in the end. This point is the trace of an edge 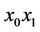 which is isolated.
which is isolated.
QED.
Remark 5. It is clear that if we paint black one inner vertex in the canonical polyhedron then we get two black points on  in the end of the algorithm.
in the end of the algorithm.
3) We consider a small ball  with the center
with the center 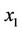 and the boundary
and the boundary 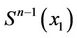 which is similar to
which is similar to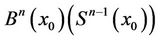 . The centers of all the n-simplexes having
. The centers of all the n-simplexes having 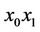 as their edge belong to the subtree L1 and the union of all the traces of this n-simplexes on
as their edge belong to the subtree L1 and the union of all the traces of this n-simplexes on  forms the canonical polyhedron on
forms the canonical polyhedron on  having one black inner vertex (the trace of isolated edge
having one black inner vertex (the trace of isolated edge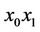 ). We apply the Proposition 6 (the Remark 5) to the
). We apply the Proposition 6 (the Remark 5) to the  and
and . As a result
. As a result 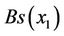 consists of two semi-isolated edges
consists of two semi-isolated edges 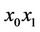 and
and .
.
Further, we iterate the process getting a broken line
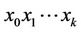 and for
and for 
 consists of two black semi-isolated edges
consists of two black semi-isolated edges 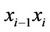 and
and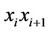 . We remark that the process of the annihilation of black simplexes in
. We remark that the process of the annihilation of black simplexes in 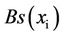 cannot bring to an appearance of a black simplex having a generic point with
cannot bring to an appearance of a black simplex having a generic point with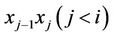 . Really, otherwise such a black simplex gives an opportunity to connect the endpoints
. Really, otherwise such a black simplex gives an opportunity to connect the endpoints 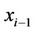 and
and 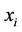 of the semi-isolated edge
of the semi-isolated edge  by a black curve which is different from
by a black curve which is different from . As a result a black loop with the semi-isolated edge
. As a result a black loop with the semi-isolated edge  as its part has been obtained and the loop is not contractible that is a contradiction to the simply connectivity of
as its part has been obtained and the loop is not contractible that is a contradiction to the simply connectivity of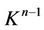 .
.
The complex  is connected therefore the broken line
is connected therefore the broken line  contains all the possible black vertexes from
contains all the possible black vertexes from 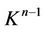 at some step of the algorithm i.e. we come to 5, 1.
at some step of the algorithm i.e. we come to 5, 1.
By the method of mathematical induction the main theorem is true for every 