Time Dependent Pressure Gradient Effect on Unsteady MHD Couette Flow and Heat Transfer of a Casson Fluid ()
1. Introduction
The study of Couette flow in a rectangular channel of an electrically conducting viscous fluid under the action of a transversely applied magnetic field has immediate applications in many devices such as magnetohydrodynamic (MHD) power generators, MHD pumps, accelerators, aerodynamics heating, electrostatic precipitation, polymer technology, petroleum industry, purification of crude oil and fluid droplets sprays. Channel flows of a Newtonian fluid with heat transfer were studied with or without Hall currents by many authors [1-10]. These results are important for the design of the duct wall and the cooling arrangements. The most important nonNewtonian fluid possessing a yield value is the Casson fluid, which has significant applications in polymer processing industries and biomechanics. Casson fluid is a shear thinning liquid which has an infinite viscosity at a zero rate of shear. Casson’s constitutive equation represents a nonlinear relationship between stress and rate of strain and has been found to be accurately applicable to silicon suspensions, suspensions of bentonite in water and lithographic varnishes used for printing inks [11-13]. Many authors [14-20] studied the flow or/and heat transfer of a non-Newtonian fluids in different geometries. The effect of time dependent pressure gradient on unsteady dusty fluid was studied by Rukmangadachari [21] in a rectangular duct and Gireesha et al. [22] in a nholonomic coordinates system.
Attia [10] studied the influence of the Hall current on the velocity and temperature fields of an unsteady Hartmann flow of a conducting Newtonian fluid between two infinite non-conducting horizontal parallel and porous plates. Attia and Sayed-Ahmed [17] studied the influence of the Hall current on the velocity and temperature fields of an unsteady Couettee flow of a conducting Casson fluid between two infinite non-conducting horizontal parallel plates with constant pressure gradient. The extension of such problem to the case of Couettee flow of non-Newtonian Casson fluid has been done in the present study. The upper plate is moving with a uniform velocity while the lower plate is stationary. The fluid is acted upon by an exponentially decaying pressure gradient, uniform suction and injection from above and below, respectively. The fluid is also, subjected to a uniform magnetic field perpendicular to the plates. The Hall current is taken into consideration while the induced magnetic field is neglected by assuming a very small magnetic Reynolds number [5]. The two plates are kept at two different but constant temperatures. This configuration is a good approximation of some practical situations such as heat exchangers, flow meters, and pipes that connect system components. The Joule and viscous dissipations are taken into consideration in the energy equation. The governing momentum and energy equations are solved numerically using the finite difference approximations. The inclusion of unsteady pressure gradient, the Hall current, the suction and injection, and the non-Newtonian fluid characteristics leads to some interesting effects on both the velocity and temperature fields.
2. Formulation of the Problem
The geometry of the problem is shown in Figure 1. The fluid is assumed to be laminar, incompressible and obeying a Casson model and flows between two infinite horizontal plates located at the y = ± h planes and extend from x = -¥ to ¥ and from z = -¥ to ¥. The upper plate is suddenly set into motion and moves with a uniform velocity Uo while the lower plate is stationary. The upper plate is simultaneously subjected to a step change in temperature from T1 to T2. Then, the upper and lower plates are kept at two constant temperatures T2 and T1 respectively, with T2 > T1. The fluid is acted upon by an exponentially decaying pressure gradient ∂p/∂x in the x-direction, and a uniform suction from above and injection from below which are applied at t = 0. A uniform magnetic field Bo is applied in the positive y-direction and is assumed undisturbed as the induced magnetic field is neglected by assuming a very small magnetic Reynolds number. The Hall effect is taken into consideration and consequently a z-component for the velocity is expected to arise. The uniform suction implies that the y-component of the velocity v0 is constant. Thus, the fluid velocity vector is given by,

The fluid motion starts from rest at t = 0, and the no-slip condition at the plates in z-direction implies that the fluid velocity has no z-component at y = ± h. The initial temperature of the fluid is assumed to be equal to T1. Since the plates are infinite in the x and zdirections, the physical quantities do not change in these directions.
The flow of the fluid is governed by the momentum equation
 (1)
(1)
where r is the density of the fluid and m is the apparent viscosity of the model and is given by
 (2)
(2)
where Kc2 is the Casson’s coefficient of viscosity and to is the yield stress. If the Hall term is retained, the current density J is given by
 (3)
(3)
where s is the electric conductivity of the fluid and b is the Hall factor [5]. Equation (3) may be solved in J to yield
 (4)
(4)
where m is the Hall parameter and m =  o. Thus, the two components of the momentum Equation (1) read
o. Thus, the two components of the momentum Equation (1) read
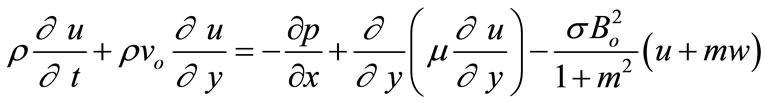 (5)
(5)
 (6)
(6)
where  is the unsteady pressure gradient The energy equation with viscous and Joule dissipations is given by
is the unsteady pressure gradient The energy equation with viscous and Joule dissipations is given by
 (7)
(7)
where cp and k are, respectively, the specific heat capacity and the thermal conductivity of the fluid. The second and third terms on the right-hand side represent the viscous and Joule dissipations respectively. We notice that each of these terms has two components. This is because the Hall effect brings about a velocity w in the z-direction. The initial and boundary conditions of the problem are given by
 at t £ 0, and
at t £ 0, and  at y =-h and y =h for t > 0
at y =-h and y =h for t > 0
u = 0 at y =-h for t > 0, u = Uo at y =h for t > 0, (8)
T = T1 at t £ 0, T = T2 at y =h and T = T1 at y = -h for t > 0 (9)
It is expedient to write the above equations in the non-dimensional form. To do this, we introduce the following non-dimensional quantities

 is the constant pressure gradient.
is the constant pressure gradient.
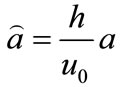 is the decaying parameter in the unsteady pressure gradient
is the decaying parameter in the unsteady pressure gradient
 is the Casson number (dimensionless yield stress)
is the Casson number (dimensionless yield stress)
 is the Reynolds number,
is the Reynolds number,
 is the suction parameter,
is the suction parameter,
 is the Prandtl number,
is the Prandtl number,
 is the Eckert number,
is the Eckert number,
 is the Hartmann number squared
is the Hartmann number squared
In terms of the above non-dimensional variables and parameters Eqs.(5-9) and (2) are, respectively, written as (where the hats are dropped for convenience);
 (10)
(10)
 (11)
(11)
 (12)
(12)
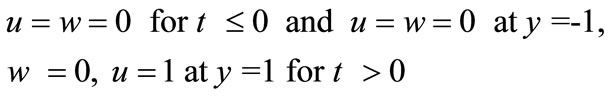 (13)
(13)
 (14)
(14)
 (15)
(15)
where 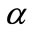 is the constant pressure gradient
is the constant pressure gradient  and a is the decaying parameter.
and a is the decaying parameter.
3. Numerical Solution
Equations (10,11,15) represent coupled system of nonlinear partial differential equations which are solved numerically under the initial and boundary conditions (13) using the finite difference approximations. A linearization technique is first applied to replace the nonlinear terms at a linear stage, with the corrections incorporated in subsequent iterative steps until convergence is reached. Then the Crank-Nicolson implicit method is used at two successive time levels [23]. An iterative scheme is used to solve the linearized system of difference equations. The solution at a certain time step is chosen as an initial guess for next time step and the iterations are continued till convergence, within a prescribed accuracy. Finally, the resulting block tridiagonal system is solved using the generalized Thomas-algorithm [23]. The energy Equation (12) is a linear non-homogeneous second-order partial differential equation whose righthand side is known from the solutions of the flow Equations (10,11,15) subject to the conditions (13). The values of the velocity components are substituted in the right-hand side of Equation (12) which is solved numerically with the initial and boundary conditions (14) using central differences and Thomas-algorithm to obtain the temperature distribution. Finite difference equations relating the variables are obtained by writing the equations at the mid-point of the computational cell and then replacing the different terms by their second order central difference approximations in the y-direction. The diffusion terms are replaced by the average of the central differences at two successive time-levels. The computational domain is divided into meshes of dimension Dt and Dy in time and space respectively as shown in Figure 2. We define the variables 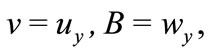
 and
and  to reduce the second order differential Equations (10,11,12) to first order differential equations. The finite difference representations for the resulting first order differential Equations (10,11) take the form (see Equations (16,17)).
to reduce the second order differential Equations (10,11,12) to first order differential equations. The finite difference representations for the resulting first order differential Equations (10,11) take the form (see Equations (16,17)).
where
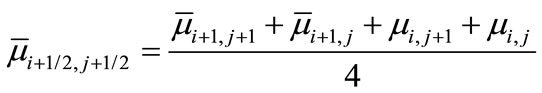 and
and

The variables with bars are given initial guesses from the previous time step and an iterative scheme is used at every time to solve the linearized system of difference equations. Then the finite difference form for the energy Equation (12) can be written as
 (18)
(18)
where DISP represents the Joule and viscous dissipation terms which are known from the solution of the momentum equations and can be evaluated at the mid point (i+1/2,j+1/2) of the computational cell. Computations have been made for α = 5, Pr = 1, Re = 1, Ha = 3 and Ec = 0.2. Grid-independence studies show that the computational domain 0
¥ and –1< y <1 can be divided into intervals with step sizes Dt = 0.0001 and Dy = 0.005 for time and space respectively. The truncation error of the central difference schemes of the governing equations is
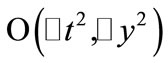 . Stability and rate of convergence are func-
. Stability and rate of convergence are func-
tions of the flow and heat parameters. Smaller step sizes do not show any significant change in the results. Convergence of the scheme is assumed when all of the unknowns u, v, w, B, θ and H for the last two approximations differ from unity by less than 10-6 for all values of y in –1 < y < 1 at every time step. Less than 7 approximations are required to satisfy this convergence criteria for all ranges of the parameters studied here.
4. Results and Discussions
Figures 3-5 show the variation of the velocity components u and w and the temperature θ at the central

plane of the channel (y = 0) with time. These figures show the results for various values of the decaying parameter a = 0, 1 and 2 and for yield stress tD = 0.0, 0.05 and 0.1. In these figures S = 1 and m = 3. Figure 3 shows that u decreases with increasing a for all values of tD. It is observed also that the time at which u reaches its steady state value decreases with increasing a for a > 0 but that occurs earlier for constant pressure gradient (a = 0). Increasing tD increases u for all values of a but with
small differences.
In Figure 4, the velocity component w decreases with increasing a. This figure indicates that the influence of tD on w depends on t and becomes more clear when the decaying parameter a = 0 but this influence is small for large a. It is observed that increasing tD more decreases w for a = 0. Figure 5 shows that the influence of a on θ depends on t. It is observed that increasing a decreases θ
while it is not greatly affected by changing tD. The figure shows also that the time at which θ reaches its steady state value decreases with increasing a while it is not greatly affected by changing tD.
Figures 6-8 show the profiles of the velocity components u and w and the temperature θ, respectively, for various values of time a and for t = 0.2, 1, and 2. The figures are evaluated for m =3, tD = 0.05 and S = 1. It is clear from Figures 6 and 7 that the effect of decaying
 (a) t = 0.2
(a) t = 0.2 (b) t = 1
(b) t = 1 (c) t = 2
(c) t = 2
Figure 6. Effect of decaying parameter a on the time development of the velocity u for various values of t (m = 3, S = 1, τD = 0.05 ).
parameter a on u and w depends on t and y. Figure 6 shows that, for small t, increasing a decreases u (with small differences) for all values of y and a. It is also observed that increasing a (a > 0) decreases u for all values of y with significant differences at medium and large t. It is also observed that the constant pressure gradient (a = 0) is greatly different from unsteady pressure gradients (a > 0). This can be attributed to the fact that increasing a will decrease the pressure gradient which mainly generates
 (a) t = 0.2
(a) t = 0.2 (b) t = 1
(b) t = 1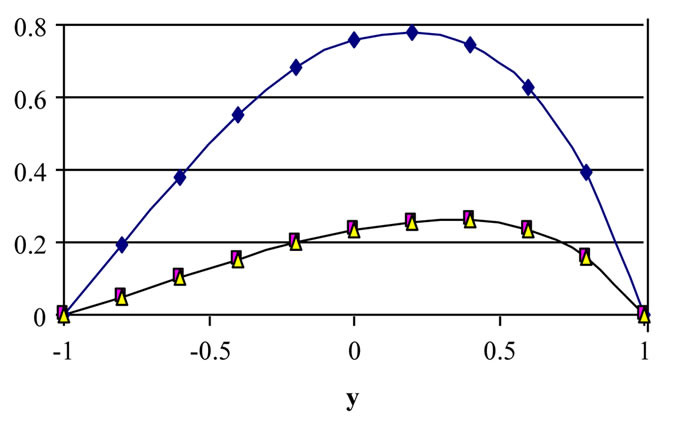 (c) t = 2
(c) t = 2

Figure 7. Effect of decaying parameter a on the distribution of w with y for various values of t (m = 3, S = 1, τD = 0.05 ).
the velocity u. Figure 7 shows that, for small t, increasing a increases w (with no significant differences ) for all y. For large t, increasing a decreases w (with no signifycant difference between a=1 and a=2) for all y. The figures show also that the velocity components u and w do not reach their steady state monotonically. The velocities u and w increase with time up till a maximum value and then decrease up to the steady state. Figure 8 shows that the temperature profile does not reach its steady state
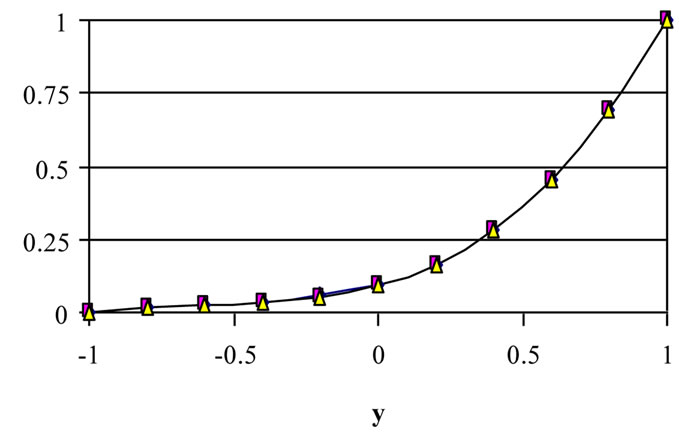 (a) t = 0.2
(a) t = 0.2 (b) t = 1
(b) t = 1 (c) t = 2
(c) t = 2

Figure 8. Effect of decaying parameter a on the distribution of w q with y for various values of t (m = 3, S = 1, τD = 0.05 ).
monotonically. Increasing a decreases θ for all y and t. It is observed also that the velocity component u reaches the steady state faster than w which, in turn, reaches the steady state faster than θ. This is expected as u is the source of w, while both u and w act as sources for the temperature.
Figures 9-11 show the variation of the velocity components u and w and the temperature θ at the central
plane of the channel (y = 0) with time for various values of the Hall parameter m and for tD = 0.0, 0.05, and 0.1. In these figures S = 0. Figure 9 shows that u increases with increasing m for all values of tD as the effective conductivity (s /(1+m2)) decreases with increasing m which reduces the magnetic damping force on u. It is observed also from the figure that the time at which u reaches its steady state value increases with increasing m. Increasing
tD increases u for all m and its effect on u becomes more pronounced for higher values of m. In Figure 10 the velocity component w increases with increasing m as w is a result of the Hall effect. On the other hand, at small times, w decreases when m increases. This happens due to the fact that, at small times w is very small and then the source term of w is proportional to (m u/(1+m2) ) which decreases with increasing m (m > 1 ). This accounts for
the crossing of the curves of w with t for all values of tD. Figure 10 indicates that the influence of tD on w depends on t and becomes more clear when m is large. It is observed that, increasing tD decreases w and increasing m increases w. Figure 11 shows that the influence of m on θ depends on t. Increasing m decreases θ at small times,
but this is reversed at large times. This is due to the fact that, for small times, u and w are small and an increase in m increases u but decreases w. Then, the Joule dissipation which is also proportional to (1/1+m2) decreases. For large times, increasing m increases both u and w and, in turn, increases the Joule and viscous dissipations. This accounts for the crossing of the curves of θ with time for
all values of tD. It is also observed that increasing tD decreases the temperature θ for all values of m. This is because increasing tD decreases both u and w and their gradients which decreases the Joule and viscous dissipations. The figure shows also that the time at which θ reaches its steady state value increases with increasing m while it is not greatly affected by changing tD.
Figures (12-14) present the profiles of the velocity components u and w and the temperature θ for variousvalues of time t and for tD = 0.0, 0.05 and 0.1. The fig-
ures are evaluated for m = 3 and S = 1. It is clear from Figures 12 and 13 that the effect of yield stress tD on u and w depends on t and y. Figure 12 shows that, for small t, increasing the yield stress tD decreases u for small y, but this is reversed for large y. As time develops, increasing tD increases u for all y. Figure 13 shows that increasing tD increases w for all values of y, but increasing tD more decreases w for large y.
For large t, increasing tD decreases w for small t and all values of y. This can be attributed to the fact that increasing tD will delay the attainment of maxima of u and w. It is also observed, from Figures 12 and 13, that the velocity components u and w do not reach their steady state monotonically. Figure 14 shows that the temperature profile does not reach its steady state monotonically. Increasing tD increases θ for all y and t as a result of increasing the dissipations. It is observed also that the velocity component u reaches the steady state faster than w which, in turn, reaches the steady state faster than θ. This is expected as u is the source of w, while both u and w act as sources for the temperature.
5. Conclusions
A finite difference method is used to solve the transient Couette flow and heat transfer of a Casson non-Newtonian fluid under the influence of unsteady pressure gradient and uniform magnetic field. In the present work, we study Hall effect. The effects of the decaying parameter a, Casson yield stress tD, and the Hall parameter m on the velocity and temperature distributions are studied. The decaying parameter a affects the main velocity components u and w and the temperature θ. The Hall term affects the main velocity component u in the x-direction and gives rise to another velocity component w in the z-direction. The results show that the influence of the parameters a and tD on u and w depend on time and the Hall parameter m. It is also found that the effect of m on w and θ depends on time for all values of tD which accounts for a crossover in the w-t and θ-t graphs for various values of m. The effect of m on the magnitude of θ depends on tD and becomes more pronounced in case of small tD. It is also found that the effect of a on the magnitude of θ depends on tD and becomes more pronounced in case of smalltD.