1. Introduction
The dark energy (cosmological constant, Λ-term) problem might be solved by the introduction of the holographic principle into physics [1] or, more exactly, by the introduction of the entropic force [2]. In any case, it is definitely necessary to associate dark energy (DE) with the vacuum energy of the Universe, the equation of state of which is
. Practically, it is an experimental fact [3,4]. In the field equations, the cosmological constant (Λ-term) was introduced by A. Einstein almost 100 years ago as a property of space:
(1)
If we move the Λ-term to the right-hand side of this equation, then it will be a form of energy that has been named DE because we do not know the exact physical nature of this form of energy. The unsolved problem of DE has even created a crisis of physics related to the large difference (123 orders) between the density of this form of energy at the moment of the Universe’s creation (z = ∞) and present-day density (z = 0).
Many authors have noted that the vacuum energy of the present Universe at small red shifts (z < 1) must be low and positive [5-8]. Here, we want to demonstrate in which physical processes the enormous reduction in the vacuum energy (123 orders) take place and also to show inevitability of the vacuum energy’s evolution. We argued that the Universe spent the vacuum energy for its expansion, for the organization of new microstates throughout the entire process, but in the initial period of its evolution, other processes (phase transitions) were more effective in providing this reduction. At first, it is necessary to define the total vacuum energy’s density (Λ). It is:
(2)
where the subscript “QF” denotes quantum fields and the subscript “GVC” is the gravitational vacuum condensate.
2. Quantum Regime
Probably, our Universe has emerged as a result of a tunnelling process after a bounce from a singularity in the presence of oscillations, and further arrived at a Friedman regime through a quantum regime [9]. In the quantum regime, phase transitions as a mechanism for inducing an enormous reduction of vacuum energy have already been discussed by R. Bousso [10]. Phase transitions in the early Universe produced condensates of quantum fields that compensated for the positive vacuum energy of the Universe by 78 orders of magnitude because the equation of state of any vacuum condensate is p = −ρ (here, p is pressure). A probable chain of phase transitions was mentioned some times before [9,11]. In any case two last phase transitions should be:
Moreover, already on the Planck scale, the 3-dimensional topological defects (wormholes) of a gravitational vacuum condensate diminished the positive initial Λ- term [12]:
(3)
where: c3 is a constant and 
Note also that in the supersymmetric vacuum of our model, the energy density of a boson field (ρbos) and the energy density of a fermion field (ρfer) have different signs, and the total vacuum energy might be, formally, equal to zero:
(4)
Later, this supersymmetry was broken, and it is likely that at that moment 
~ 1064 GeV4 (supersymmetry is broken if and only if the cosmological constant (vacuum energy) is positive). That is, in the early stages of the Universe’s evolution, the compensation of the vacuum energy was necessary, obligatory. We cannot calculate well the energy density for all condensates of the probable chain [9,11], but the last two condensates of quantum fields in the framework of the Standard Model may be calculated exactly. These condensates are called the Higgs condensate in the theory of the electro-weak interaction (ρEW) and the quark-gluon condensate in quantum chromodynamics (ρQCD). For the Higgs condensate, we have [11,12]:
(5)
Here, besides the masses of known bosons, the mass of the t-quark enters the equation. The first term is a proper condensate (g is a gauge constant). The second term in this formula is responsible for vacuum polarization. If the Higgs mass is mH = 125 GeV, then ρEW ≈ −(100 GeV)4. For the quark-gluon condensate, we have [11-13]:
. (6)
A numerical estimate can also be obtained: ρQCD ≈ −(265 МeV)4. Only the quark-hadron phase transition “quenches” near 10 orders of the vacuum energy density’s magnitude; that is, 
. Phase transitions in the early Universe have quenched more than 1078 orders of the vacuum energy,
.
Such a tremendous reduction in the vacuum energy terminated the moment when the Universe was only ~10−6 sec old; moreover, at that moment, the Universe lost its chiral symmetry SU(3)L × SU(3)R [14] and it had the vacuum energy’s density ~10−2 (GeV)4 or ~ 1016 g×cm−3. The chiral QCD symmetry is not an exact symmetry, and pseudo-Goldstone bosons are a physical manifestation of this symmetry breaking. The spontaneous breaking of this symmetry leads to the appearance of an octet of pseudoscalar Goldstone states in the spectrum of particles (π-mesons). In this process, π-mesons are excitations of the ground state, and they determine this ground state [14]. Long ago, Ya. Zel’dovich [15] attempted to calculate a nonzero vacuum energy for our Universe in terms of the quantum fluctuations of particles as a high-order effect. He inserted the proton or electron mass into his formula, but the result was not satisfactory. The situation changes if the average mass of π-mesons (mπ =138.04 MeV) is inserted into Zel’dovich’s formula:
(7)
In this formula, all constants are known, and using the definition of a critical density, we can obtain a value for ΩΛ:
(8)
If the Hubble constant is H0 = 70.5 (km×sec−1/Mpc), then ΩΛ ~ 0.73. After reaching the energy ~150 MeV (the end of the last phase transition), the vacuum energy stopped decreasing rapidly, and at a later time, the vacuum energy decreased very slowly. However, even at that moment, there was still a large quantitative difference between the vacuum energy density values at the moment of chiral symmetry breakdown and these in the modern epoch:
(9)
3. Classical Regime
Here, we arrive to an important point in our consideration. The Universe expands, and new microstates are produced for any of its components. The particle density dilutes as 1/R3, but the law of vacuum dilution is otherwise (1/R2). The vacuum energy is spent to produce new microstates. The physical and mathematical basis of this statement must be discussed because it is an entirely new idea. The physical bases are: 1) the holographic principle [1]; 2) the idea that gravitation on the macroscopic scale is a manifestation of vacuum thermodynamics [16]; and 3) the idea that thermodynamics of a de Sitter universe is similar to the thermodynamics of a black hole in special coordinates [17]. The Ostrogradsky-Gauss theorem employed in cosmology by G. Smoot [18] provides a mathematical basis. According to the holographic principle, the physics of a 3D system may be described by the theory acting on its 2D boundary. J. Bekenstein [19] has shown that the entropy (the number of microstates) of a black hole is equal to 1/4 of its event horizon area expressed in Planck units. In cosmology, E. Verlinde’s idea [2] of an entropic force is better for understanding holography. At temperature T, the entropic force F of a gravitational system is given as:
(10)
where: ΔS is the change in the entropy at a displacement Δx. The information about a holographic system is given by N bits forming a gas N = 4S/kB, where kB is the Bol’tzmann constant). A more detailed discussion can be found in the paper [20]. C. Balazs & I. Szapidi [21] obtained a formula for determining the Universe’s energy density in the holographic limit: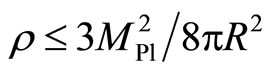
, where R is the apparent horizon of the Universe. Using the W. Fischler & L. Susskind [22] cosmic holographic conjecture, C. Balazs & I. Szapidi asserted that the entropy of the Universe (S) is restricted by its “surface” measured in Planck units:
. It is easy to see that a relationship between the energy density and the number of quantum states (microstates) of the Universe is established because new quantum states arise due to expansion. Thus, in the holographic limit, the vacuum energy density of the Universe is related to its entropy by the simplest formula:
, (11)
which in some sense, is the Friedmann equation. By substituting into (11) the size of the observed Universe R ~ 1028 cm, we obtain the energy density in the holographic limit: ρ ~ 10−57, if MPl = 1. In the quantum regime of the Universe’s evolution, the holographic concept does not hold. The Universe entered the classical regime after the last phase transition at E ~ 150 MeV. If RQCD ~ 3 × 104 cm, then (RQCD/R)2 ~ 10−47. The simplest approximation formula for calculating the vacuum energy density ρΛ(z) in the classical regime of the Universe’s evolution is:
(12)
R(z) can be calculated using the “cosmological calculator” of E. Wright [23]. As demonstrated in [24], we have already performed calculations of the vacuum energy’s evolution from z = 0 to z = 1011. At small red shifts (z < 1), a smooth increase in the vacuum energy density must take place with increasing z, which is not easy to detect. This difference is greater at high read shifts (z > 1) which may be detected. This shorten table is taken of our paper [24].
From the foregoing table time is in milliards years from creation of the Universe. If these trends will not be detected in the nearest DE experiments, DES, LSST, Euclid, Big BOSS [25], then it is likely that the DE may be a mixture of vacuum energy and a condensate of another field. The other field may be a field of dark matter that is a rather natural possibility. Moreover, the decay of dark energy into dark matter may determine the coincidence problem. However, this notion pertains to another approach and other trends [26].
4. Summary
Thus, in the quantum regime of the Universe’s evolution, in 10−6 sec, the vacuum energy density decreased by 78 orders of magnitude from the Planck value because in that epoch the positive vacuum energy’s density was affected by negative contributions producing vacuum condensates. By the end of the last phase transition, the vacuum energy density was ~1016 g×cm−3, which marked an important moment—the Universe lost its chiral symmetry. In the classical regime of the Universe’s evolution, the vacuum energy density decreased by 47 orders in 4 × 1017 sec. Vacuum energy was spent for the organization of new microstates as the Universe expanded (the existence of the entropic force required the energy expense). Between the quantum and classical regimes, there was a transitional stage, which was unfortunately impossible to calculate well and additional investigations of this stage were necessary, of course. In light of the foregoing discussion, any remaining doubts regarding the evolution of the vacuum energy should disappear; that is, the vacuum energy of the Universe is a dynamical quantity ρΛ(z). Note that cosmology with a time-dependent vacuum was already considered in the papers [27,28]. Finally, the nearly exact compensation of the 123 orders of the vacuum energy of the Universe in natural physical processes imparted reliability to these estimates, and the crisis of physics related the vacuum energy (cosmological constant, Λ-term) of the Universe may be, thus, overcome.
A separate, very important issue is vacuum stability. Seven years ago, we introduced a condition of vacuum stability into the Standard Model [12]. The mutual compensation of positive and negative contributions to the vacuum energy density in the regime of supersymmetry is prohibited by the condition of vacuum stability (see also Equation (5) for the Higgs vacuum). For the Higgs mass mH ~ 125 GeV, the stability of vacuum up to the Planck scale requires the introduction of new physics beyond the Standard Model [29]; furthermore, the asymptotic safety of the Standard Model vacuum must also be realized [30]. An absolute stable vacuum might arise if mH > 129 GeV [31], and it is likely that we live in only a metastable vacuum. Another important issue is the equation of state. The most recent measurements [4] show that w < −1, but to date, mistakes in the measurements of w indicate that w = −1 for the flat Universe [32].