Nemytskii Operator in the Space of Set-Valued Functions of Bounded φ-Variation ()
1. Introduction
In [1], it was proved that every globally Lipschitz Nemytskii operator

mapping the space  into itself admits the following representation:
into itself admits the following representation:

where  is a linear continuous set-valued function and
is a linear continuous set-valued function and  is a set-valued function belonging to the space
is a set-valued function belonging to the space . The first such theorem for singlevalued functions was proved in [2] on the space of Lipschitz functions. A similar characterization of the Nemytskii operator has also been obtained in [3] on the space of set-valued functions of bounded variation in the classical Jordan sense. For single-valued functions it was proved in [4]. In [5,6], an analogous theorem in the space of set-valued functions of bounded
. The first such theorem for singlevalued functions was proved in [2] on the space of Lipschitz functions. A similar characterization of the Nemytskii operator has also been obtained in [3] on the space of set-valued functions of bounded variation in the classical Jordan sense. For single-valued functions it was proved in [4]. In [5,6], an analogous theorem in the space of set-valued functions of bounded  -variation in the sense of Riesz was obtained. Also, they proved a similar result in the case in which that the Nemytskii operator N maps the space of functions of bounded
-variation in the sense of Riesz was obtained. Also, they proved a similar result in the case in which that the Nemytskii operator N maps the space of functions of bounded  -variation in the sense of Riesz into the space of set-valued functions of bounded
-variation in the sense of Riesz into the space of set-valued functions of bounded  -variation in the sense of Riesz, where
-variation in the sense of Riesz, where , and
, and  is globally Lipschitz. In [7], they showed a similar result in the case where the Nemytskii operator
is globally Lipschitz. In [7], they showed a similar result in the case where the Nemytskii operator  maps the space
maps the space  of setvalued functions of bounded
of setvalued functions of bounded  -variation in the sense of Riesz into the space
-variation in the sense of Riesz into the space  of set-valued functions of bounded
of set-valued functions of bounded  -variation in the sense of Riesz and
-variation in the sense of Riesz and  is globally Lipschitz.
is globally Lipschitz.
While in [8], we generalize article [6] by introducing a weight function. Now, we intend to generalize [7] in a similar form we did in [8], i.e., the propose of this paper is proving an analogous result in which the Nemytskii operator  maps the space
maps the space  of setvalued functions of bounded
of setvalued functions of bounded  -variation in the sense of Riesz with a weight
-variation in the sense of Riesz with a weight  into the space
into the space  of set-valued functions of bounded
of set-valued functions of bounded  -variation in the sense of Riesz with a weight
-variation in the sense of Riesz with a weight  and
and  is globally Lipschitz.
is globally Lipschitz.
2. Preliminary Results
In this section, we introduce some definitions and recall known results concerning the Riesz  -variation.
-variation.
Definition 2.1 By a  -function we mean any nondecreasing continuous function
-function we mean any nondecreasing continuous function  such that
such that  if and only if
if and only if , and
, and  as
as .
.
Let  be the set of all convex continuous functions that satisfy Definition 2.1.
be the set of all convex continuous functions that satisfy Definition 2.1.
Definition 2.2 Let  be a normed space and
be a normed space and  be a
be a  -function. Given
-function. Given  be an arbitrary (i.e., closed, half-closed, open, bounded or unbounded) fixed interval and
be an arbitrary (i.e., closed, half-closed, open, bounded or unbounded) fixed interval and  a fixed continuous strictly increasing function called a it is weight. If
a fixed continuous strictly increasing function called a it is weight. If , we define the (total) generalized
, we define the (total) generalized  -variation
-variation 
 of the function
of the function  with respect to the weight function
with respect to the weight function  in two steps as follows (cf. [9]). If
in two steps as follows (cf. [9]). If  is a closed interval and
is a closed interval and  is a partition
is a partition  of the interval I (i.e.,
of the interval I (i.e., ), we set
), we set

Denote by  the set of all partitions of
the set of all partitions of , we set
, we set

If  is any interval in
is any interval in , we put
, we put

The set of all functions of bounded generalized  - variation with weight
- variation with weight 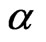 will be denoted by
will be denoted by
 .
.
If , and
, and ,
,  ,
,  , the
, the  -variation
-variation , also written as
, also written as , is the classical
, is the classical  -variation of
-variation of  in the sense of Riesz [10], showing that
in the sense of Riesz [10], showing that  if and only if
if and only if  (i.e.,
(i.e.,  is absolutely continuous) and its almost everywhere derivative
is absolutely continuous) and its almost everywhere derivative  is Lebesgue
is Lebesgue  -summable on
-summable on . Recall that, as it is well known, the space
. Recall that, as it is well known, the space  with I,
with I,  and
and  as above and endowed with the norm
as above and endowed with the norm 
is a Banach algebra for all .
.
Riesz’s criterion was extended by Medvedev [11]: if , then
, then  if and only if
if and only if 
and . Functions of bounded generalized
. Functions of bounded generalized  -variation with
-variation with  and
and  (also called functions of bounded Riesz-Orlicz
(also called functions of bounded Riesz-Orlicz  -variation) were studied by Cybertowicz and Matuszewska [12]. They showed that if
-variation) were studied by Cybertowicz and Matuszewska [12]. They showed that if , then
, then
 and that the space
and that the space

is a semi-normed linear space with the LuxemburgNakano (cf. [13,14]) seminorm given by
 .
.
Later, Maligranda and Orlicz [15] proved that the space  equipped with the norm
equipped with the norm

is a Banach algebra.
3. Generalization of Medvedev Lemma
We need the following definition:
Definition 3.1 Let  be a
be a  -function. We say
-function. We say  satisfies condition
satisfies condition  if
if
 (1)
(1)
For φ convex, (1) is just . Clearlyfor
. Clearlyfor  the space
the space  coincides with the classical space
coincides with the classical space  of functions of bounded variation. In the particular case when
of functions of bounded variation. In the particular case when  and
and 
 , we have the space
, we have the space 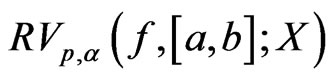 of functions of bounded Riesz
of functions of bounded Riesz  -variation. Let
-variation. Let 
be a measure space with the Lebesgue-Stieltjes measure defined in  -algebra
-algebra  and
and

Moreover, let  be a function strictly increasing and continuous in
be a function strictly increasing and continuous in . We say that
. We say that  has
has  - measure 0, if given
- measure 0, if given  there is a countable cover
there is a countable cover  by open intervals of
by open intervals of , such that
, such that
 .
.
Since  is strictly increasing, the concept of “
is strictly increasing, the concept of “ measure
measure ” coincides with the concept of “measure 0” of Lebesgue. [cf. [16],
” coincides with the concept of “measure 0” of Lebesgue. [cf. [16],  25].
25].
Definition 3.2 (Jef) A function  is said to be absolutely continuous with respect to
is said to be absolutely continuous with respect to , if for every
, if for every , there exists
, there exists  such that
such that

for every finite number of nonoverlapping intervals ,
,  with
with  and
and
 .
.
The space of all absolutely continuous functions , with respect to a function
, with respect to a function  strictly increasing, is denoted by
strictly increasing, is denoted by . Also the following characterization of [17,18] is well-known:
. Also the following characterization of [17,18] is well-known:
Lemma 3.3 Let . Then
. Then  exists and is finite in
exists and is finite in , except on a set of
, except on a set of  -measure
-measure .
.
Lemma 3.4 Let . Then
. Then  is integrable in the sense Lebesgue-Stieltjes and
is integrable in the sense Lebesgue-Stieltjes and

Lemma 3.5 Let  such that satisfies the
such that satisfies the 
condition. If , then
, then  is
is  -absolutely continuous in
-absolutely continuous in , i.e.,
, i.e.,

Also the following is a generalization of Medvedev Lemma [11]:
Theorem 3.6 (Generalization a Medvedev Lemma) Let  such that satisfies the
such that satisfies the  condition,
condition,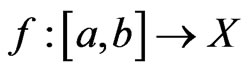 . Then 1) If
. Then 1) If  is
is  -absolutely continuous on
-absolutely continuous on  and
and
 then
then
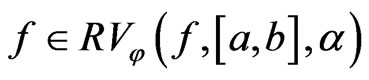
and
 .
.
2) If  (i.e.,
(i.e., ), then
), then  is
is  -absolutely continuous on
-absolutely continuous on  and
and
 .
.
Proof. ) Since
) Since  is
is  absolutely continuous, there exists
absolutely continuous, there exists  a.e. in
a.e. in  by Lemma 3.3. Let
by Lemma 3.3. Let ,
, 

by Lemma 3.4 and  is strictly increasing
is strictly increasing

using the generalized Jenssen’s inequality

Let  be any partition of interval
be any partition of interval ; then
; then

and we have
 .
.
Thus .
.
 ) Let
) Let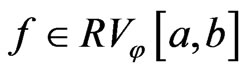 . Then
. Then  is
is  -absolutely continuous on
-absolutely continuous on  by Lemma 3.5 and
by Lemma 3.5 and  exist a.e. on
exist a.e. on .
.
For every , we consider
, we consider

a partition of the interval  define by
define by
 ,
, .
.
Let  be a sequence of step functions, defined by
be a sequence of step functions, defined by 

 converge to
converge to  a.e. on
a.e. on . It is sufficient to prove
. It is sufficient to prove  in those points where
in those points where  is
is  - differentiable and different from
- differentiable and different from ,
,  for
for , i.e., in
, i.e., in

For , and each
, and each , there exists
, there exists  such that
such that , so
, so

Therefore,  is a convex combination of points
is a convex combination of points

Now if , then
, then  and
and  and since
and since  is
is  -differentiable for
-differentiable for , the expressions
, the expressions

tend  to which is
to which is  -differentiable from
-differentiable from  in
in . So results
. So results

Since 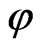 is continuous, we have
is continuous, we have

Using the Fatou’s Lemma and definition of  sequence, results that
sequence, results that

By definition from 

which is what we wished to demonstrate.
Corollary 3.7 Let  such that satisfies the
such that satisfies the  condition, then
condition, then  if and only if
if and only if  is
is  -absolutely continuous on
-absolutely continuous on  and
and
 .
.
Also

Corollary 3.8 Let  such that satisfies the
such that satisfies the  condition. If
condition. If , then
, then  is
is  -absolutely continuous on
-absolutely continuous on  and
and

4. Set-Valued Function
Let  be the family of all non-empty convex compact subsets of
be the family of all non-empty convex compact subsets of  and
and  be the Hausdorff metric in
be the Hausdorff metric in , i.e.,
, i.e.,

where , or equivalently,
, or equivalently,

where
 (2)
(2)
Definition 4.1 Let ,
,  a fixed continuous strictly increasing function and
a fixed continuous strictly increasing function and . We say that
. We say that  has bounded
has bounded  -variation in the sense of Riesz if
-variation in the sense of Riesz if
 (3)
(3)
where the supremum is taken over all partitions  of
of .
.
Definition 4.2 Denote by
 (4)
(4)
and
 (5)
(5)
both equipped with the metric
 (6)
(6)
where

Now, let ,
,  be two normed spaces and
be two normed spaces and  be a convex cone in
be a convex cone in . Given a set-valued function
. Given a set-valued function  we consider the Nemytskii operator
we consider the Nemytskii operator  generated by
generated by , that is the composition operator defined by:
, that is the composition operator defined by:

We denote by  the space of all setvalued function
the space of all setvalued function , i.e., additive and positively homogeneous, we say that
, i.e., additive and positively homogeneous, we say that  is linear if
is linear if .
.
In the proof of the main results of this paper, we will use some facts which we list here as lemmas.
Lemma 4.3 ([19]) Let  be a normed space and let
be a normed space and let  be subsets of
be subsets of . If
. If  are convex compact and
are convex compact and  is non-empty and bounded, then
is non-empty and bounded, then
 (7)
(7)
Lemma 4.4 ([20]) Let ,
,  be normed spaces and
be normed spaces and  be a convex cone in
be a convex cone in . A set-valued function
. A set-valued function  satisfies the Jensen equation
satisfies the Jensen equation
 (8)
(8)
if and only if there exists an additive set-valued function  and a set
and a set  such that
such that
 ,
, .
.
We will extend the results of Aziz, Guerrero, Merentes and Sánchez given in [8] and [21] to set-valued functions of  -bounded variation with respect to the weight function
-bounded variation with respect to the weight function .
.
5. Main Results
Lemma 5.1 If  such that satisfies the
such that satisfies the  condition and
condition and
 then
then  is continuous.
is continuous.
Proof. Since , exists
, exists  such that
such that
 (9)
(9)
for all partitions of , in particular given
, in particular given , we have
, we have
 (10)
(10)
Since  is convex
is convex  -function, from the last inequality, we get
-function, from the last inequality, we get
 (11)
(11)
By (1),
 (12)
(12)
This proves the continuity of  at
at . Thus
. Thus  is continuous on
is continuous on .
.
Now, we are ready to formulate the main result of this work.
Main Theorem 5.2 Let ,
,  be normed spaces,
be normed spaces,  be a convex cone in
be a convex cone in  and
and  be two convex
be two convex  -functions in
-functions in , strictly increasing, that satisfy
, strictly increasing, that satisfy  condition and such that there exists constants
condition and such that there exists constants  and
and  with
with  for all
for all . If the Nemitskii operator
. If the Nemitskii operator  generated by a set-valued function
generated by a set-valued function  maps the space
maps the space
 into the space
into the space
 and if it is globally Lipschitz, then the set-valued function
and if it is globally Lipschitz, then the set-valued function  satisfies the following conditions:
satisfies the following conditions:
1) For every  there exists
there exists , such that
, such that
 (13)
(13)
2) There are functions  and
and  such that
such that
 (14)
(14)
Proof. 1) Since  is globally Lipschitz, there exists a constant
is globally Lipschitz, there exists a constant  such that
such that
 (15)
(15)
Using the definitions of the operator  and metric
and metric  we have
we have

where . In particular,
. In particular,

for all  and
and ,
,  , where
, where
 .
.
Since  and
and  satisfy
satisfy
 (16)
(16)
we obtain

Therefore
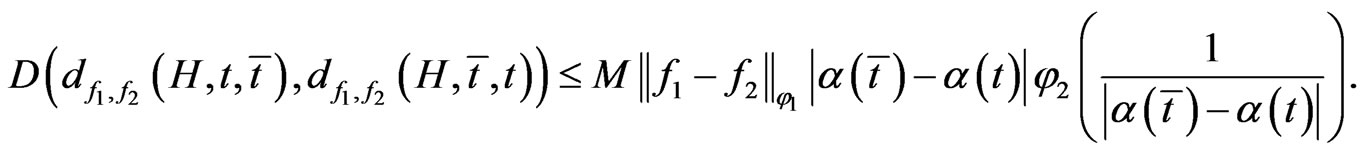 (17)
(17)
Define the auxiliary function  by:
by:
 (18)
(18)
Then  and
and

Let us fix  and define the functions
and define the functions 
 by:
by:
 (19)
(19)
Then the functions 
 and
and
 (20)
(20)
From the definition of  and
and , we have
, we have
 (21)
(21)
From (16), we get
 (22)
(22)
Hence,
 (23)
(23)
Hence, substituting in inequality (5) the particular functions 
 defined by (19) and taking
defined by (19) and taking  in (23), we obtain
in (23), we obtain
 (24)
(24)
for all .
.
By Lemma 4.3 and the inequality (24), we have

for all .
.
Now, we have to consider the case . Define the function
. Define the function  by
by
 (25)
(25)
Then the function  and
and

Let us fix  and define the functions
and define the functions 
 by
by
 (26)
(26)
Then the functions  (i = 1,2) and
(i = 1,2) and

Substituting  and
and , and consider
, and consider , we obtain
, we obtain
 (27)
(27)
for all , where
, where

By Lemma 4.3 and the above inequality, we get

for all . Define the function
. Define the function  by
by

Hence

and, consequently, for every  the function
the function  is continuous.
is continuous.
This completes the proof of part 1).
Now we shall prove that  satisfies equality 2).
satisfies equality 2).
Let us fix  such that
such that . Since the Nemytskii operator
. Since the Nemytskii operator  is globally Lipschitzian, there exists a constant
is globally Lipschitzian, there exists a constant , such that
, such that
 (28)
(28)
where . Define the function
. Define the function  by
by

The function .
.
Let us fix  and define the functions
and define the functions  by
by
 (29)
(29)
The functions 
 and
and
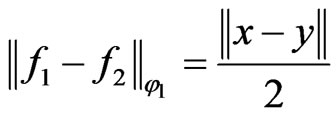 .
.
Hence, substituting in the inequality (28) the particular functions 
 defined by (29), we obtain
defined by (29), we obtain
 (30)
(30)
Since  maps
maps
 into
into then
then  is continuous for all
is continuous for all . Hence letting
. Hence letting  in the inequality (30), we get
in the inequality (30), we get
 (31)
(31)
for all  and
and .
.
Thus for all , we have
, we have
 (32)
(32)
Since  is convex, we have
is convex, we have
 (33)
(33)
for all . Thus for all
. Thus for all , the set-valued function
, the set-valued function  satisfies the Jensen Equation (33). Now by Lemma 4.4, there exists an additive set-valued function
satisfies the Jensen Equation (33). Now by Lemma 4.4, there exists an additive set-valued function  and a set
and a set , such that
, such that
 (34)
(34)
Substituting  into inequality (13), we deduce that for all
into inequality (13), we deduce that for all  there exists
there exists , such that
, such that

consequently, for every  the set-valued function
the set-valued function  is continuous, and
is continuous, and
 .
.
Since  is additive and
is additive and , then
, then  for all
for all , thus
, thus .
.
The Nemytskii operator  maps the space
maps the space  into the space
into the space , then
, then
 .
.
Consequently the set-valued function  has to be of the form
has to be of the form

where 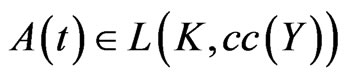 and
and
 .
.
Theorem 5.3 Let ,
,  be normed spaces,
be normed spaces,  a convex cone in
a convex cone in  and
and  be two convex
be two convex  -functions in
-functions in , strictly increassing, satisfying
, strictly increassing, satisfying 
condition and . If the Nemytskii operator
. If the Nemytskii operator  generated by a set-valued function
generated by a set-valued function
 maps the space
maps the space 
into the space  and if it is globally Lipschizian, then the set-valued function
and if it is globally Lipschizian, then the set-valued function 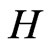 satisfies the following condition
satisfies the following condition

i.e., the Nemytskii operator is constant.
Proof. Since the Nemytskii operator  is globally Lipschizian between
is globally Lipschizian between  and the space
and the space
 , then there exists a constant
, then there exists a constant , such that
, such that
 (35)
(35)
Let us fix  such that
such that . Using the definitions of the operator
. Using the definitions of the operator  and of the metric
and of the metric , we have
, we have
 (36)
(36)
Define the auxiliary function  by
by

The function  and
and

Let us fix  and define the functions
and define the functions 
 by
by
 (37)
(37)
The functions 
 and
and

Hence, substituting in the inequality (36) the auxiliary functions 
 defined by (37), we obtain
defined by (37), we obtain
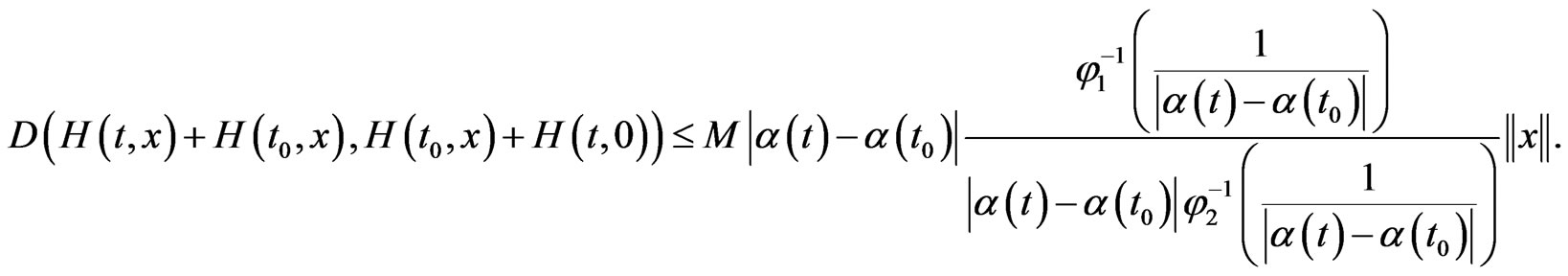
By Lemma 4.3 and the above inequality, we get

Since , letting
, letting  in the above inequality, we have
in the above inequality, we have

Thus for all  and for all
and for all , we get
, we get

Theorem 5.4 Let ,
,  be normed spaces,
be normed spaces,  a convex cone in
a convex cone in  and
and  be a convex
be a convex  - function in
- function in  satisfying the
satisfying the  condition. If the Nemytskii operator
condition. If the Nemytskii operator  generated by a set-valued function
generated by a set-valued function  maps the space
maps the space  into the space
into the space  and if it is globally Lipschizian, then the left regularization
and if it is globally Lipschizian, then the left regularization  of the function
of the function  defined by
defined by

satisfies the following conditions:
• for all  there exists
there exists , such that
, such that
• 
• 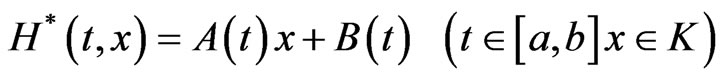 , where
, where  is a linear continuous set-valued function, and
is a linear continuous set-valued function, and .
.
Proof. We take , and define the auxiliary function
, and define the auxiliary function  by:
by:

The function  and
and

Let us fix  and define the functions
and define the functions 
 by
by
 (38)
(38)
The functions  and
and
 (39)
(39)
From the definition of  and
and , we obtain
, we obtain
 (40)
(40)
Since the Nemytskii operator  is globally Lipschitzian between
is globally Lipschitzian between
 and
and then there exists a constant
then there exists a constant , such that
, such that

for . By Lemma 4.3, substituting the particular functions
. By Lemma 4.3, substituting the particular functions 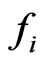
 defined by (38) in the above inequality, we obtain
defined by (38) in the above inequality, we obtain
 (41)
(41)
for all . By Lemma 4.3, we get
. By Lemma 4.3, we get
 (42)
(42)
for all  and
and .
.
In the case where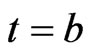 , by a similar reasoning as above, we obtain that there exists a constant
, by a similar reasoning as above, we obtain that there exists a constant , such that
, such that
 (43)
(43)
Define the function  by
by
 (44)
(44)
Hence,

By passing to the limit in the inequality (41) by the inequality (43) and the definition of  we have for all
we have for all  that there exists
that there exists , such that
, such that

Now we shall prove that  satisfies the following equality
satisfies the following equality

where  is a linear continuous set-valued functions, and
is a linear continuous set-valued functions, and
 .
.
Let us fix  such that
such that . Define the partition
. Define the partition  of the interval
of the interval  by
by

The Nemytskii operator  is globally Lipschitzian between
is globally Lipschitzian between  and
and , then there exists a constant
, then there exists a constant , such that
, such that
 (45)
(45)
where

and
 .
.
We define the function  in the following way:
in the following way:

The function  and
and
 .
.
Let us fix  and define the functions
and define the functions  by:
by:
 (46)
(46)
The functions  and
and
 .
.
Substituting in the inequality (45) the particular functions 
 defined in (46), we obtain
defined in (46), we obtain
 (47)
(47)
Since the Nemytskii operator  maps the spaces
maps the spaces  into
into , then for all
, then for all , the function
, the function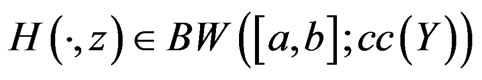 . Letting
. Letting  in the inequality (47), we get
in the inequality (47), we get

for all  and
and . By passing to the limit when
. By passing to the limit when , we get
, we get

Since  is a convex function, then
is a convex function, then

Thus for every , the set-valued function
, the set-valued function  satisfies the Jensen equation. By Lemma 4.4 and by the property (a) previously established, we get that for all
satisfies the Jensen equation. By Lemma 4.4 and by the property (a) previously established, we get that for all  there exist an additive set-valued function
there exist an additive set-valued function  and a set
and a set , such that
, such that

By the same reasoning as in the proof of Theorem 5.2, we obtain that
 and
and .
.
6. Acknowledgements
This research was partly supported by CDCHTA of Universidad de Los Andes under the project NURR-C- 547-12-05-B.