1. Introduction
In a very recent paper [1], the effects of a magnetic field on the two components of the total angular momentum of an elementary one-fermion state, for simplicity assumed to be that of one electron, have been analyzed in the framework of quantum field theory. In the special case of a weak and classic magnetic field, it has been shown that these effects can be very simply computed under the two fundamental assumptions that 1) the considered electromagnetic interaction is of the “minimal” form, and 2) that fermions satisfy the Dirac equation (the motivations that deeply support the assumption 1 have been exposed in [1]). In particular, it has been shown that the modifications of the two (orbital and spin) components of the angular momentum are strictly connected and calculable in a similar way. In the final part of the paper, it has been proposed that a certain analogy might exist between the two considered (orbital and spin) components of the angular momentum of the elementary matter system, the fermion, and the two components (histonic octamer and DNA) components of the elementary organic system, the nucleus.
The aim of this paper is that of showing that in fact an impressive analogy exists between the processes of modifications of the observable properties of an elementary matter component and of the observable properties of an elementary organic component, induced by an external interacting environment. The latter one can be of several different natures in the organic case. In our quantum field theory example we shall be limited to the consideration of the effects that would be produced by an external magnetic field. The main reason is that for this specific case the available theoretical formalism allows us to compute very simply and rigorously the produced effects. This restriction does not represent a problem in our opinion, since the possibility of detecting the effects on the organic nucleus of a weak magnetic field appears to be seriously considered at the moment [2].
It will be essential at this point to illustrate the basic motivation of this paper. This is the existence of a deep and, in our opinion, impressive analogy between the basic constituent of the organic nucleus the histonic octamer,and that of the matter fermion, the field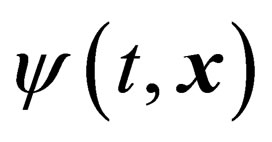 . Strictly speaking, both constituents are not rigorously “elementary”. In fact, they are both containing four “ultimate” components. These are the four histones (H2A, H2B, H3 and H4) for the octamer and the four components of the spinor field
. Strictly speaking, both constituents are not rigorously “elementary”. In fact, they are both containing four “ultimate” components. These are the four histones (H2A, H2B, H3 and H4) for the octamer and the four components of the spinor field  for the fermion field. More rigorously, the octamer is actually “built” as an octamer of 8 histones making four coupled “dimers”. Analogously, the complete description of the matter fermion is given by the four-component
for the fermion field. More rigorously, the octamer is actually “built” as an octamer of 8 histones making four coupled “dimers”. Analogously, the complete description of the matter fermion is given by the four-component 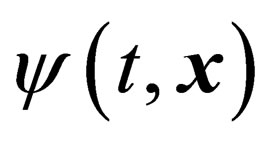 and by its four-component complex conjugate
and by its four-component complex conjugate , which makes even in this case eight “ultimate” entities to be requested for a complete description of the system.
, which makes even in this case eight “ultimate” entities to be requested for a complete description of the system.
Starting from the initial analogy, the scheme of the paper becomes now the following. In the next Section 2, the epigenetic process for an organic nucleus will be quickly reviewed. The main purpose will be that of showing the different stages of the process, that begins with a modification of the histones followed by a produced modification of the DNA. In rigorous analogy, we shall show in Section 3 that the modification of all the observable properties of an elementary fermion are the consequence of an “initial” modification of the four field components  that produce the observable effects. This will be shown in some detail, deriving all the various effects in a concise but necessarily rigorous way. In the final Section 4, a few general features of the fermion modification will be considered, and the possibility of analogies with the fascinating medical research on epigenetics will be proposed.
that produce the observable effects. This will be shown in some detail, deriving all the various effects in a concise but necessarily rigorous way. In the final Section 4, a few general features of the fermion modification will be considered, and the possibility of analogies with the fascinating medical research on epigenetics will be proposed.
2. Features of the Organic Epigenetics Process
In this Section 2, we shall very briefly summarize, with the unique specific purpose of searching for possible analogies with what will be illustrated in the next Section 3, some features of the fascinating organic epigenetic process, We shall start saying that nowadays, in the study of organism proneness to diseases, the epigenetic regulation is acquiring more and more relevance. In this process, an active regulation of the organism with respect to the surrounding environment is implied.
There exist several epigenetic mechanisms. In this paper we shall concentrate on the histonic octet and on its capacity of regulating the DNA expression. As it is known, the histonic octet is built by four histonic couples, the “dimers”. The histones are classified by the terms ,
,  ,
,  and
and . One tetramer is made by two
. One tetramer is made by two  and
and  dimers, a second one is made by
dimers, a second one is made by  and
and  dimers. The two tetrameters join themselves and build the histonic octamer around which the DNA twines, creating the nucleosome.
dimers. The two tetrameters join themselves and build the histonic octamer around which the DNA twines, creating the nucleosome.
The histones have a tail that extends outside the nucleosome. The histone tails may undergo various processes (e.g. methylation) that will generate variations of the histones links with DNA. These variations of the DNA “intrinsic structure” i.e. of its twining around the octamer will modify the genic expression, that will be regulated to become more suited to the existing environment.
The process of histones modification can be in general stimulated by the surrounding environment. In particular, it appears nowadays [2] that a possible source of modifications is the presence of a weak magnetic field. This is the starting point of our quantum field theory description, that follows in the next Section 3.
3. The Fermion “Magnetization” Process
We shall consider some properties of an elementary fermion system, and treat as a particularly relevant example that of the electron elementary particle. In the quantum field description that we shall use, the relevant entity will be the four-dimensional spinor field . We shall call
. We shall call  the four field components, that will be denoted for simplicity by the term: psinons, and use the conventional column representation:
the four field components, that will be denoted for simplicity by the term: psinons, and use the conventional column representation:
 (1)
(1)
The corresponding “conjugate” field will be also conventionally defined by the row representation
 (2)
(2)
where the star denotes complex conjugation. In the expression of certain observables, we shall have to make use of the four Dirac matrices denoted as usually with the notation ,
,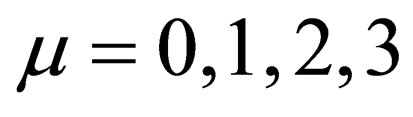 . The adopted properties of these matrices, as well as the technical details of the field operations, are rigorously taken by the Peskin-Schroeder book [3].
. The adopted properties of these matrices, as well as the technical details of the field operations, are rigorously taken by the Peskin-Schroeder book [3].
As the starting point of this section, we shall consider three physical observables of the spinor system, i.e. the orbital and spin components of the angular momentum  and the total energy
and the total energy  for a free system. This expression can be easily derived from the Noether theorem [4]. In general, they are given by certain space integrals that contain expressions of the kind
for a free system. This expression can be easily derived from the Noether theorem [4]. In general, they are given by certain space integrals that contain expressions of the kind


 (3)
(3)
where,  is one of the observables and
is one of the observables and  is an operator connecting
is an operator connecting  and
and  which will be a certain combination of scalars and
which will be a certain combination of scalars and  matrices. In the case of a fermion field,
matrices. In the case of a fermion field,  will be time-independent, as well as
will be time-independent, as well as  (in general,
(in general,  and
and  will not be separately conserved in time).
will not be separately conserved in time).
For the purposes of this paper, we shall now write the expressions of the three considered observables in terms of the four components  and
and . After some lengthy but simple manipulations it is easy to derive the following expressions for
. After some lengthy but simple manipulations it is easy to derive the following expressions for :
:
 (4)
(4)
where  is the external vector product
is the external vector product
 (5)
(5)
and  is the gradient vector operator
is the gradient vector operator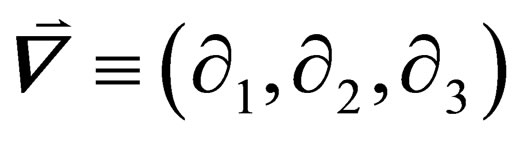 . In this case,
. In this case,  is a “fermion scalar” in the sense that it does not contain
is a “fermion scalar” in the sense that it does not contain  matrices. As one sees, the
matrices. As one sees, the  observable can be expressed by an integration where four different couples of elementary spinors appear. In particular, we could define the combinations as
observable can be expressed by an integration where four different couples of elementary spinors appear. In particular, we could define the combinations as ,
, 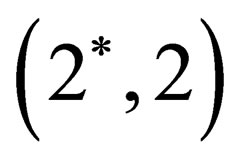 ,
,  ,
, . Note that in every couple a spinon
. Note that in every couple a spinon 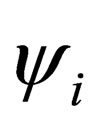 and one complex conjugate
and one complex conjugate  appear.
appear.
In a similar way, the expression of the spin angular momentum  can be derived. It will be less simple because the spin content is expressed by certain
can be derived. It will be less simple because the spin content is expressed by certain 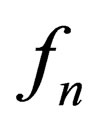 that are products of
that are products of  matrices. After a straightforward calculation one can write the following expressions for the three
matrices. After a straightforward calculation one can write the following expressions for the three  spin components (in the notation where
spin components (in the notation where )
)
 (6)
(6)
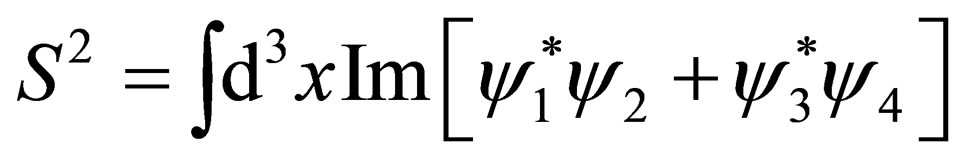 (7)
(7)
 (8)
(8)
where Re and Im denote the real and imaginary parts of the various brackets. One sees that the couples that appear in  and
and  are different from those of
are different from those of  and
and . In particular,
. In particular,  and
and  contain couples that we shall indicate as
contain couples that we shall indicate as  and
and , more precisely the real or imaginary parts of the products (that are not real, not being diagonal as those of
, more precisely the real or imaginary parts of the products (that are not real, not being diagonal as those of  and
and ). Note that the relative signs of the four couples of
). Note that the relative signs of the four couples of  are different from those of the same couples in
are different from those of the same couples in .
.
As a final example, we have computed the expression of . This is the most complicated one, since this observable is a sum of operators that either do not contain or do contain
. This is the most complicated one, since this observable is a sum of operators that either do not contain or do contain  matrices. The result of this calculation is the following one
matrices. The result of this calculation is the following one
 (9)
(9)
where,  and
and 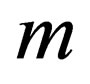 is the electron mass. As one sees, he various components of
is the electron mass. As one sees, he various components of  depend on several couples of
depend on several couples of  that are sometimes different from the couples that appear in
that are sometimes different from the couples that appear in  and
and . In general, the dependence of
. In general, the dependence of ,
,  and
and  on the possible psinon
on the possible psinon 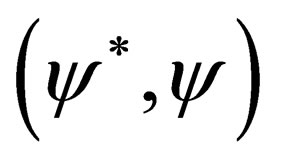 couples is drastically different.
couples is drastically different.
We are now ready to express in terms of the various psinon couples the effect of a magnetic field on the previous observables. For the special purposes of this paper we have first considered a classic electromagnetic field, defined by four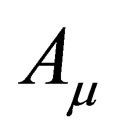 ,
,  and supposed to be of low intensity. To derive the electromagnetic effect, we have first (A) imposed that the electromagnetic overall effects can be described by using the “minimal interaction” prescription. This corresponds to the replacement of the conventional derivative
and supposed to be of low intensity. To derive the electromagnetic effect, we have first (A) imposed that the electromagnetic overall effects can be described by using the “minimal interaction” prescription. This corresponds to the replacement of the conventional derivative  with the “covariant” one
with the “covariant” one :
:
 (10)
(10)
where  is the electron electric charge, conventionally chosen as negative. We have discussed in [1] the deep motivations (Higgs mechanism as a request for local gauge transformations invariance) that make the “minimal “choice Equation (10) to be reliable, and we shall not repeat them here. Next, we have imposed (B) that the fermions obey the Dirac equation. These two choices have led us to the calculation of the electromagnetic effects. To obtain the latter ones, we have first computed the variation of the basic spinons. Following the procedure illustrated in [1], we have obtained the results:
is the electron electric charge, conventionally chosen as negative. We have discussed in [1] the deep motivations (Higgs mechanism as a request for local gauge transformations invariance) that make the “minimal “choice Equation (10) to be reliable, and we shall not repeat them here. Next, we have imposed (B) that the fermions obey the Dirac equation. These two choices have led us to the calculation of the electromagnetic effects. To obtain the latter ones, we have first computed the variation of the basic spinons. Following the procedure illustrated in [1], we have obtained the results:
 (11)
(11)
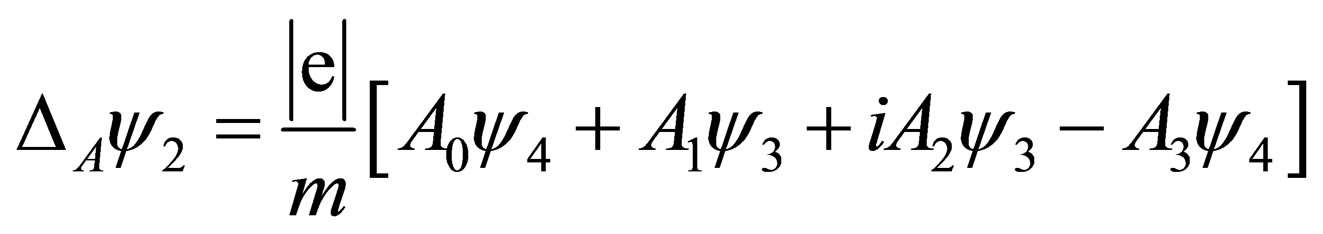 (12)
(12)
 (13)
(13)
 (14)
(14)
Equations (11)-(14) are general and contain the electromagnetic four-vector potential ,
,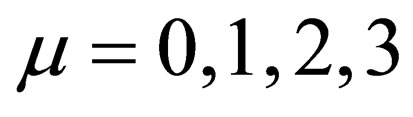 . Our main interest is concentrated on the effects of a “weak” classic magnetic field alone. With this purpose, we have considered the case of a constant classic magnetic field along a given direction, e.g. the
. Our main interest is concentrated on the effects of a “weak” classic magnetic field alone. With this purpose, we have considered the case of a constant classic magnetic field along a given direction, e.g. the  axis
axis
 (15)
(15)
In this case, we shall have
 (16)
(16)
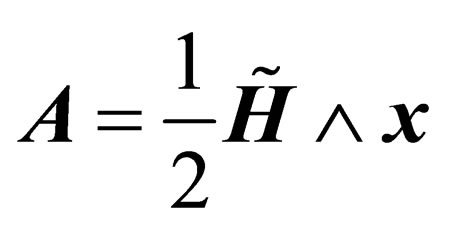 (17)
(17)
Notice that the three-vector potential  is transverse, i.e.
is transverse, i.e. . Thus,
. Thus,  satisfies the Coulomb gauge condition. Under the assumption that
satisfies the Coulomb gauge condition. Under the assumption that  is “weak”, we have only retained in the magnetic effects the contributions of “lowest order” in the magnetic field. With this choice, all the magnetic effects may be written in terms of the free psinons
is “weak”, we have only retained in the magnetic effects the contributions of “lowest order” in the magnetic field. With this choice, all the magnetic effects may be written in terms of the free psinons ,
,  , whose expression is supposed to be known, and corresponds to the “initial” state of the fermion. Working in this spirit, we have derived expressions for the “magnetic shifts” that we shall indicate with the notation
, whose expression is supposed to be known, and corresponds to the “initial” state of the fermion. Working in this spirit, we have derived expressions for the “magnetic shifts” that we shall indicate with the notation . More precisely, we have obtained for the
. More precisely, we have obtained for the  shifts:
shifts:
 (18)
(18)
 (19)
(19)
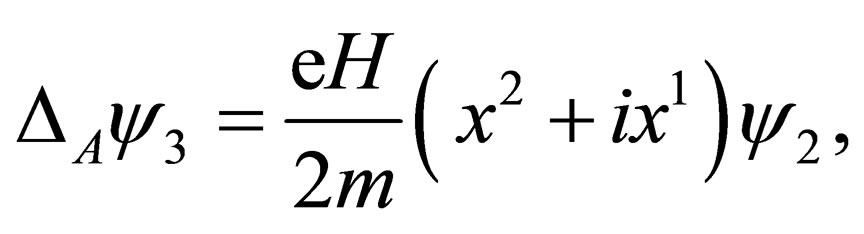 (20)
(20)
 (21)
(21)
Starting from those shifts, we have obtained for the three components of 
 (22)
(22)
 (23)
(23)
 (24)
(24)
In the case of , we obtain:
, we obtain:
 (25)
(25)
 (26)
(26)
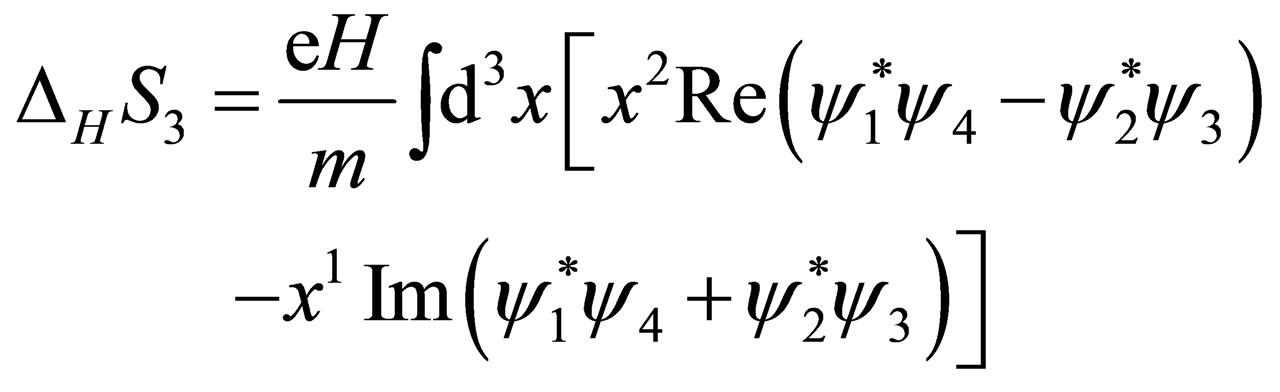 (27)
(27)
Finally, we have found for the total energy  the following expression
the following expression
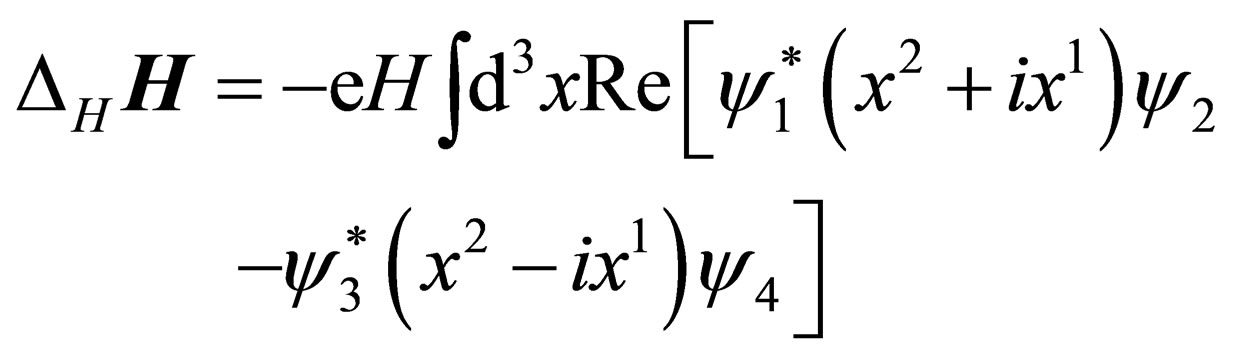 (28)
(28)
Equations (22)-(28) are the main result of this paper. from their expression we can derive a number of general and special properties that appear to us possibly relevant. We shall list and discuss those properties in the final Section 4.
4. Conclusions
We have derived in the previous sections a number of effects that would be produced by a classic magnetic field on all the observable properties of our elementary quantum fermion system, assumed for simplicity to be that of one electron. Our final expression have treated the case of a weak and constant field, which makes all calculations particularly simple, but the extension to a general variable field could be performed in a straightforward, albeit non-trivial, way. Our results exhibit a number of special features that we shall briefly summarize in what follows.
1) All the physical observables of the system can be expressed as integrals where different couples of “associated” psinons appear. In particular, the expressions of different observables contain different associated pairs of psinons.
2) The effects of the considered magnetic field on each observable are proportional to the field strength and can be also expressed as integrals of associated psinon couples.
3) In the considered case of a weak magnetic field, all the field effects can be expressed as integrals over the free psinon components pairs.
4) In our calculations, one sees that all the changes of the various observables can be derived from changes of the various psinons. To compute the latter ones, it is essential to require the validity of the Dirac equation and of the minimal coupling theoretical scheme, the latter one being derived from the principle of local gauge invariance.
5) The magnetic change of each psinon is due to variations of different psinons. In the special case of a constant field, one sees that two different couples of psinons are mutually interacting, i.e. the  and
and  couples.
couples.
6) In all the expressions that we derived for the magnetic effects, an integral appears over the three-dimensional space. In practice, though, the only relevant integration region is the one where  and
and  are simultaneously non-vanishing. We can name this region the “overlapping volume”. This will qualitatively depend on the “geometrical shape” of the considered system.
are simultaneously non-vanishing. We can name this region the “overlapping volume”. This will qualitatively depend on the “geometrical shape” of the considered system.
Having computed all the magnetic effects on the various observables, we have tried to see whether some of the effects will remain constant in time. For what concern the total energy of the system, this conservation follows from the same requests that are necessary in the free case, i.e. the vanishing of the energy flux at infinity. A different situation would be met for the case of the three components of the total angular momentum, sum of the orbital and of the spin terms. In the free case, all the three sums (i.e. not the separate orbital and spin vectors) are time independent as a consequence of the requested rotational invariance. Having introduced a constant magnetic field with a fixed direction, that we chose as the  axis, we expect a conservation of the only corresponding component of the total angular momentum, consequence of the surviving rotational invariance around
axis, we expect a conservation of the only corresponding component of the total angular momentum, consequence of the surviving rotational invariance around . We have performed the calculation of the time variation of
. We have performed the calculation of the time variation of  in our model. As a matter of fact, this variation is vanishing as a crucial consequence of the validity of the Dirac equation, that allows to compute all the involved psinon variations. One sees in particular that time variation of the orbital momentum exactly cancels that of the spin component, leaving an overall constant non vanishing effect that can be derived from our formulas (24), (27).
in our model. As a matter of fact, this variation is vanishing as a crucial consequence of the validity of the Dirac equation, that allows to compute all the involved psinon variations. One sees in particular that time variation of the orbital momentum exactly cancels that of the spin component, leaving an overall constant non vanishing effect that can be derived from our formulas (24), (27).
We enclose a brief description of the cancellation mechanism since it is, in our opinion, worth to be illustrated. By taking into account the explicit form of the magnetic field, one finds that each component of the total angular momentum varies of a quantity

 (29)
(29)
From this general expression, it is immediate to recover
 (30)
(30)
where,  is the position in the transverse plane,
is the position in the transverse plane,  and
and  can be interpreted as the charge density and the charge current, respectively.
can be interpreted as the charge density and the charge current, respectively.
To compute the time derivative of  we use the Dirac equation and the continuity equation for the charge density and current, in this way one finds
we use the Dirac equation and the continuity equation for the charge density and current, in this way one finds
 (31)
(31)
By working out the explicit form of the time derivative in the last term in the square bracket, we find
 (32)
(32)
The first term in Equation (32) cancel the first term in Equation (31). The remaining term is vanishing after integration:
 (33)
(33)
In fact, the spin tensor current has a vanishing trace, i.e. .
.
Having verified that the  component of the total angular momentum remains constant in time, we have tried to investigate whether the same property holds, in general, for the separate components. In the free case, as we have said, this does not happen unless the quantum fields satisfies the spatial conditions
component of the total angular momentum remains constant in time, we have tried to investigate whether the same property holds, in general, for the separate components. In the free case, as we have said, this does not happen unless the quantum fields satisfies the spatial conditions  [5]. In our considered case, the time variations of the spin component
[5]. In our considered case, the time variations of the spin component  is given, as one can easily verify, by the following expression
is given, as one can easily verify, by the following expression
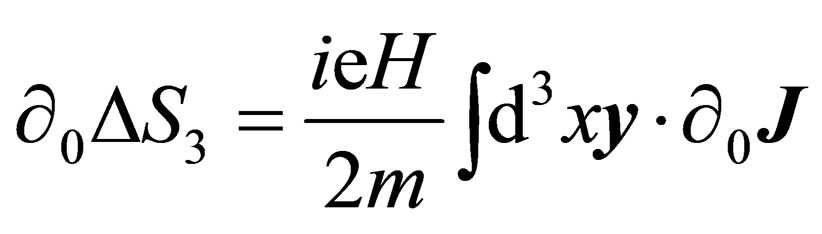 (34)
(34)
After integration by parts, and disregarding a surface term, one sees that the specific condition of time independence for the spin component  (and also, necessarily, for the orbital component
(and also, necessarily, for the orbital component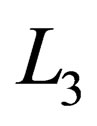 ) is given by the condition
) is given by the condition
 (35)
(35)
The vanishing of 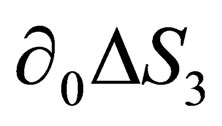 can thus be considered as the consequence of an orthogonality property of the system, that can be seen as a sort of “symmetry “around the direction of the magnetic field.
can thus be considered as the consequence of an orthogonality property of the system, that can be seen as a sort of “symmetry “around the direction of the magnetic field.
Note also, to conclude, that the constant effect on S3 is produced by (see Equation (27)) by products of the “mutually” interacting couples 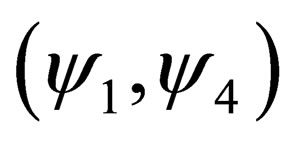 and
and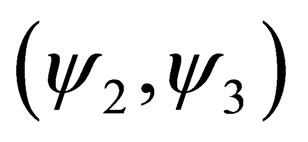 .
.
The previous remarks can be considered as a summary of the (in our opinion) most relevant features of the toy-model that we have personally proposed to be interpreted as a “magnetic quantum epigenetics” description. The search of possible analogies with the fascinating medical treatment of the epigenetic process is certainly beyond our purposes. There are, though, a few features of the model description that we consider, possibly, intriguing. First of all, the numerical coincidence of the number of psinons and histones. In the quantum field theory case, the fact that there exist four different elementary components of the relevant field is an immediate consequence of the value of the electron spin equal 1/2. One deep question would certainly be that of understanding why the elementary nucleus contains four different histones. Another property of the quantum toy-model is that the variations of the psinons, induced by the magnetic field, generate the variations of the observables, in particular of the orbital and spin angular momenta. In our extremely personal view, we like to consider the electron spin, a measurable and totally space independent property of the system, as the “analogue” of the nucleus DNA. In this personal view, the remaining orbital angular momentum would correspond to the nucleus epigenome. As an effect of the surrounding perturbation, e.g. a magnetic field, the epigenome changes and generates modifications of the DNA “shape”. In our toy-model the modifications of the  component of the spin,
component of the spin,  , would remain constant as a consequence of a specific symmetry. We have insisted on the word “symmetry” because, as a matter of fact, such a property does exist for a nucleus tetramer, which exhibits the so-called “pseudo-dyad” symmetry of the dimers [6].
, would remain constant as a consequence of a specific symmetry. We have insisted on the word “symmetry” because, as a matter of fact, such a property does exist for a nucleus tetramer, which exhibits the so-called “pseudo-dyad” symmetry of the dimers [6].
It would be, in our opinion, rather impressive that the effect of DNA of a weak magnetic field remained in some cases constant. This would certainly require a dedicated experimental analysis, that might be actually performed. In fact, the effect on organic cell of a weak magnetic field have been already considered in the literature [7].
To make a final (and very personal) statement, we believe that our results do indicate a possible fascinating set of “analogies” between the evolution of an elementary matter component and that of elementary living component. This belief would correspond to an impressive (in our opinion) statement that we found in a book written by A. Lima-de-Faria [8]. The statement is:
“The evolution of living systems is a continuation of that of the physical world, whose essence is constituted by the combination and overlapping of a limited number of initial forms and functions”.
In this spirit, we also feel that an extension of our toy-model to a more realistic and complex physical system would be welcome. We are already working in this direction.