Seismic Damage Estimation of an Actual Reinforced Concrete Structure Using Subset MCMC ()
1. Introduction
The final goal of structural design is quantitative estimation of structural safety. However, quantitative damage estimation, i.e., failure probability, subject to an individual strong motion is not obtained from the procedure based on a structural design code. Because a specific ground motion is ordinary derived from a acceleration spectrum, which reflects properties of many ground motions predicted at each site, given in the design code. Therefore, we know only whether a structure is safe for the above specific ground motion.
Recently, the subset simulation for reliability estimation of structures subject to strong motions was proposed [1]. A basic idea of the subset simulation is to reduce the computation time by replacing small failure probability into the product of conditional failure probabilities.
In this paper, the above simulation is adopted for reliability estimation of an actual reinforced building with 11 stories under the conditions of uncertainty on material properties such as story stiffness and story yield strength.
2. Failure Probability Using Subset MCMC
The concept of subset simulation proposed by Siu-Kui Au are as follows [2]. Given a failure event , let
, let  be a decreasing sequence of failure events so that
be a decreasing sequence of failure events so that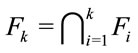 ,
, .
.
By the definition of conditional probability, we have
 . (1)
. (1)
The above equation means that a failure probability is replaced by the production of sequence conditional probabilities. There, P(F1) is obtained from standard MCS (Monte Calro Simulation), and P(F2) ~ P(Fm) are obtained from subset MCMC (Markov Chain Monte Calro). Under the condition that the limit state function Z is negative, failure probability using subset methods is expressed by the following equation.
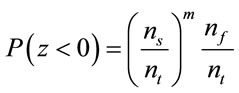 . (2)
. (2)
where : number of samples generated in subset
: number of samples generated in subset 
 : number of samples defined in subset
: number of samples defined in subset
 , for example
, for example .
.
 : number of samples satisfing
: number of samples satisfing  in the last chain level,
in the last chain level, .
.
 : level number of Markov chain.
: level number of Markov chain.
On the other hand, a conditional probability density function is expressed by the following equation.
 . (3)
. (3)
where : index function,
: index function,  if
if  is included in
is included in , others
, others .
.
3. Ground Motions and Analytical Model
Table 1 shows input ground motions. Ground motions of No.1 - No.7 were observed at HKD180 point of K-net. No.8 - No.11 are design ground motions which are often used for dynamic analysis in Japan. In this study, these ground motions are normalized so that PGV (Peak Ground Velocity) leads to 50 kine, then we call them the level 2 ground motions in Japan. Figure 1 shows an example of normalized ground motions, and Figure 2 shows the response spectra of No.8 - No.11 ground motions.
Analytical model is an actual reinforced concrete residential building with 11 stories and two spans in X and Y direction. Table 2 shows the structural heights and the story weights of this model.
In nonlinear dynamic response analysis, it is assumed that a skeleton curve is tri-linear, and a hysteresis rule is masing type. In Rayleigh damping ratio, it is assumed that first and second damping of natural vibration mode is 5%. Time-stepping solver for the equation of motion adopts Wilson’s θ method (θ = 1.42).
As structural failure index, two indexes of MCDR (Maximum Column Drift Ratio) and MDD (Maximum Ductility Demand) are considered. In addition, it is assumed that strong sway observed on tall buildings after ground motion shake down does not occur about 11 stories building, and the following cutoff time is used.
 . (4)
. (4)

Figure 1. JMA Kobe 1995 NS normalized earthquake.

Figure 2. Response spectrum of No.8 - No.11. Damping ratio: h = 5%.
where peak-time is the latest time among occurrence times of maximum absolute amplitude on PGA (Peak Ground Acceleration), PGV (Peak Ground Velocity) and PGD (Peak Ground Displacement).
In the subset simulation, it is assumed that material properties are uncertain and input ground motions are deterministic. Concretely, first and second story stiffness, story yield strength, i.e., SK1, SK2, SSy, at each floor are treated as uncertain variables. Furthermore, it is assumed that only two variables in (SK1, SK2) or (SK2, SSy) vary at a simulation in order to simplify. Table 3 shows the mean values of these three variables specified by transforming the relationship between interstory drift and story shear force, which is derived from pushover analy-

Table 2. Structural height and story weight of analytical model.

Table 3. Story yield strength and 1st and 2nd story stiffness (mean value).
sis, into a tri-linear skeleton curve. Each parameter is the set of i.i.d. (independent identically distributed) according with the following Gaussian distribution:
 . (5)
. (5)
where : coefficient of variation, it is assumed that
: coefficient of variation, it is assumed that  is equal to 5% for the combination (SK1, SK2) and 2% for the combination (SK2, SSy).
is equal to 5% for the combination (SK1, SK2) and 2% for the combination (SK2, SSy).
Calculation flows are as follows. Firstly, standard MCS is executed. Response analysis of  times per a simulation is repeated in MCS, and then a weakest floor is specified. In the weakest floor, frequencies that interstory drift or ductility demand shows maximum values is the biggest among all floors.
times per a simulation is repeated in MCS, and then a weakest floor is specified. In the weakest floor, frequencies that interstory drift or ductility demand shows maximum values is the biggest among all floors.
Secondly, the subset simulation is executed. Samples of the weakest floor are generated using MCMC. : the number of samples generated about each subset level, is set 600 based on convergence diagnostics by Raftery and Lewis [3]. And to the samples of other floors, the values generated in MCS are applied in order to reduce computation time for the parallel simulation mentioned later.
: the number of samples generated about each subset level, is set 600 based on convergence diagnostics by Raftery and Lewis [3]. And to the samples of other floors, the values generated in MCS are applied in order to reduce computation time for the parallel simulation mentioned later.
4. Basic Response Properties
Natural elastic period of analytical model is 0.764 (sec) in X direction, and 0.8204 (sec) in Y direction. Firstly, we describe response results subject to the 50 kine normalized 1995 Kobe NS shown in Figure 1.
Figures 3(a) and (b) show the restoring force and the ductility demand in X and Y direction frame. According to the restoring force, it is clarified that drift occurs and its degree in X direction frame is slightly larger than Y
 (a)
(a) (b)
(b)
Figure 3. Restoring force and ductility demand. (a) X direction frame; (b) Y direction frame.
direction. Under the comparison of ductility demand in X and Y direction, the damage of X direction frame is obviously larger than Y direction frame. The tendency was same about results subject to other earthquake motions. Therefore, in estimation of failure probability mentioned later, only X direction frame will be described. Incidentally, the ductility demand  in X direction frame is over 1 at other floors except the top floor.
in X direction frame is over 1 at other floors except the top floor.
Figure 4 shows time variation of energy dissipated in X direction frame. According to this figure, yielding does not yet occur although cracking occurs in the top floor, however yielding occurs in first floor. Figure 5 shows the ductility demands of No.1 - No.11 input motions. According to this figure, the maximum values of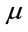 , i.e.,
, i.e.,  are over 1 for other ground motions except No.1, 4, 5, and
are over 1 for other ground motions except No.1, 4, 5, and  appear not only at lower story but also at upper story or middle story.
appear not only at lower story but also at upper story or middle story.