1. Introduction
All the graphs considered here are finite and undirected with no loops and multiple edges. As usual  and
and  denote the number of vertices and edges of a graph
denote the number of vertices and edges of a graph , respectively. In general, we use
, respectively. In general, we use  to denote the subgraph induced by the set of vertices
to denote the subgraph induced by the set of vertices  and
and  and
and  denote the open and closed neighbourhoods of a vertex
denote the open and closed neighbourhoods of a vertex , respectively. The degree of the vertex
, respectively. The degree of the vertex  in
in  is denoted by
is denoted by 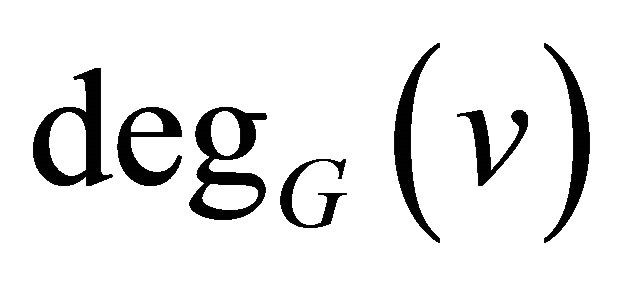 or
or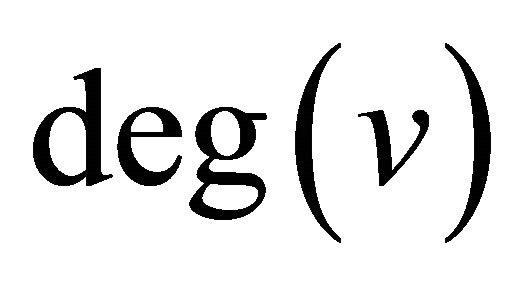 . For graph theoretic terminology, we refer to Harary [1]. The degree equitable domination has been studied in [2]. A subset
. For graph theoretic terminology, we refer to Harary [1]. The degree equitable domination has been studied in [2]. A subset  of
of  is called an equitable dominating set of a graph
is called an equitable dominating set of a graph  if for every
if for every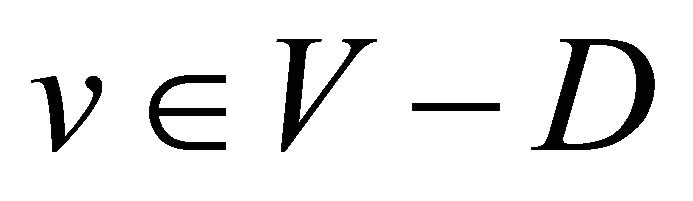 , there exists a vertex
, there exists a vertex  such that
such that  and
and
 . The minimum cardinality of such a dominating set is denoted by
. The minimum cardinality of such a dominating set is denoted by  and is called the equitable domination number of
and is called the equitable domination number of . The set
. The set 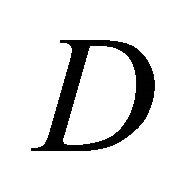 is minimal if for any vertex
is minimal if for any vertex ,
,  is not an equitable dominating set of
is not an equitable dominating set of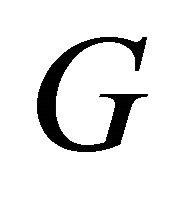 . The equitable neighbourhood of
. The equitable neighbourhood of  denoted by
denoted by  is defined as
is defined as
 and
and
 . The cardinality of
. The cardinality of  is denoted by
is denoted by  and it is called equitable degree of the vertex
and it is called equitable degree of the vertex 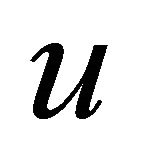 in
in . The maximum and minimum equitable degree of
. The maximum and minimum equitable degree of  are denoted respectively by
are denoted respectively by 
and . That is
. That is ,
,
 . An edge
. An edge  is called an equitable edge if
is called an equitable edge if . A subset
. A subset  of
of
 is called an equitable independent set, if
is called an equitable independent set, if  contains no vertices
contains no vertices  such that
such that . If a vertex
. If a vertex
 satisfies
satisfies  for all
for all then
then  is in the equitable dominating set. Such vertices are called equitable isolated vertices.
is in the equitable dominating set. Such vertices are called equitable isolated vertices.
Let  be a simple graph with
be a simple graph with  vertices
vertices . Then its adjacency matrix
. Then its adjacency matrix 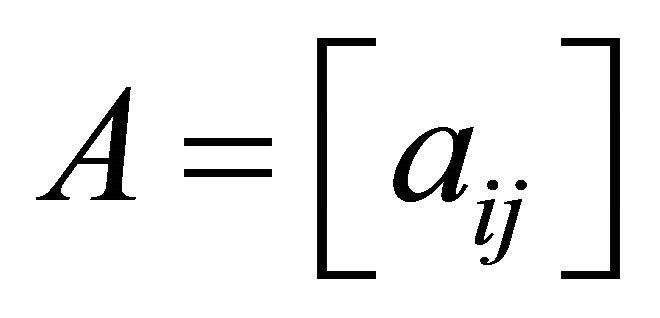 is a
is a  matrix whose entries
matrix whose entries  are given by
are given by

In the same way, the degree equitable adjacency matrix denoted by  is a
is a 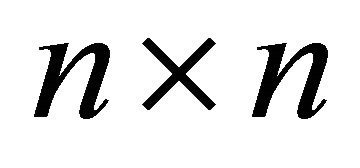 matrix whose entries
matrix whose entries  are given by
are given by

where The equitable adjacency between any two vertices  in
in  is defined as follows: the vertex
is defined as follows: the vertex  is equitable adjacent to
is equitable adjacent to  if and only if
if and only if  is adjacent to
is adjacent to
 and also
and also .
.
Degree equitable adjacency has interesting applications in the context of social networks. In a network, nodes with nearly equal capacity may interact with each other in a better way. In society, persons with nearly equal status, tend to be friendly. In industry, employees with nearly equal powers form associations and move closely. Equitability among citizens in terms of wealth, health, status, etc is the goal of a democratic nation. These ideas motivated us in this paper to study the degree equitability of a graph by defining and studying some basic properties of degree equitable connectivity, degree equitable regularity, and degree equitable completeness of a graph. Some new families of graphs and some interesting results are obtained. In this paper for brevity we use equitable instead of degree equitable.
2. Elementary Results
Let 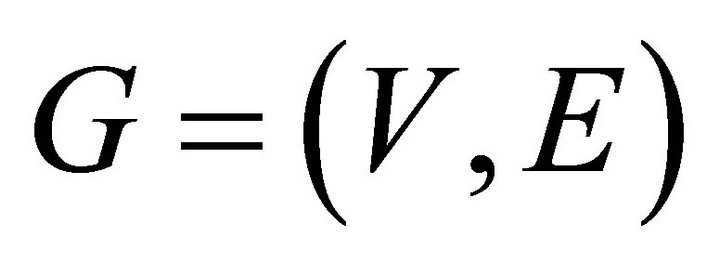 be a graph. An equitable walk is defined as a finite alternating sequence of vertices and equitable edges, beginning and ending with vertices, such that each equitable edge is incident with the vertices preceding and following it. No equitable edge appears (is covered or traversed) more than once in the equitable walk. A vertex, however, may appear more than once. An equitable walk which begin and end at the same vertex called closed equitable walk. An equitable walk is not closed if the terminal vertices are distinct. An open equitable walk in which no vertex appears more than once is called an equitable path. The number of edges in an equitable path is called the length of the equitable path. A closed equitable walk in which no vertex (except the initial and the final vertex) appears more than once is called an equitable circuit.
be a graph. An equitable walk is defined as a finite alternating sequence of vertices and equitable edges, beginning and ending with vertices, such that each equitable edge is incident with the vertices preceding and following it. No equitable edge appears (is covered or traversed) more than once in the equitable walk. A vertex, however, may appear more than once. An equitable walk which begin and end at the same vertex called closed equitable walk. An equitable walk is not closed if the terminal vertices are distinct. An open equitable walk in which no vertex appears more than once is called an equitable path. The number of edges in an equitable path is called the length of the equitable path. A closed equitable walk in which no vertex (except the initial and the final vertex) appears more than once is called an equitable circuit.
Now, we prove some results representing the relations between the sum of the equitable degree of the vertices, the number of edges and the number of equitable edges.
Theorem 2.1. For any graph  with
with 
vertices  and
and  edges,
edges, .
.
Further, the equality hold if and only if every edge in 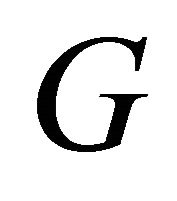 is equitable edge.
is equitable edge.
Proof. We have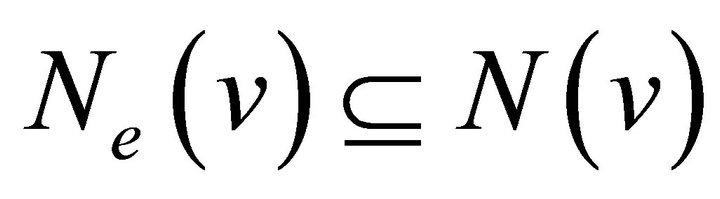 , for any vertex
, for any vertex 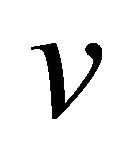 in a graph
in a graph . Then it is clear that
. Then it is clear that 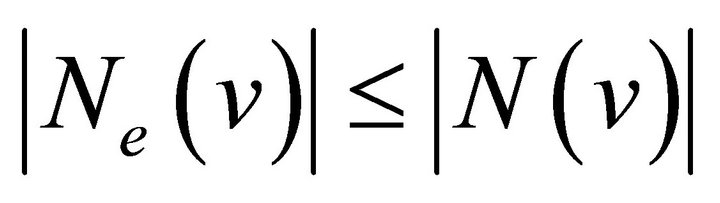 and we have:
and we have:

similarly,

which implies

Hence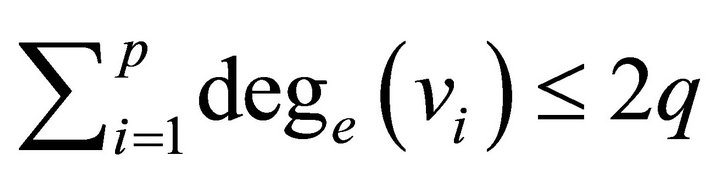 . Further, if every edge in
. Further, if every edge in  is equitable edge, then
is equitable edge, then  for any vertex
for any vertex 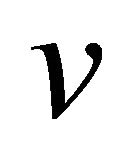 in
in  that means
that means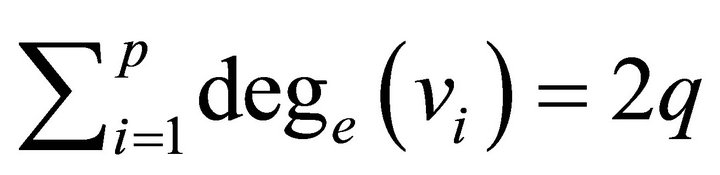 . The converse is obvious, if
. The converse is obvious, if , then every edge in
, then every edge in  is equitable edge.
is equitable edge.
For any graph , the number of equitable edge denoted by
, the number of equitable edge denoted by  is called the equitable size. The vertex
is called the equitable size. The vertex  is called equitable odd vertex (equitable even vertex) if
is called equitable odd vertex (equitable even vertex) if 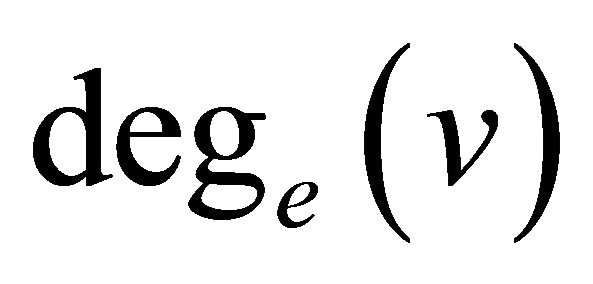 is odd number (even number).
is odd number (even number).
Theorem 2.2. The sum of the equitable degrees of a graph is twice the number of equitable edges in it, that is
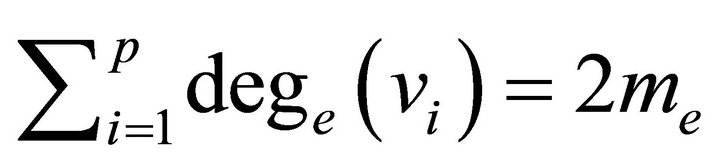 .
.
Proof. Let  be a graph. Then any equitable edge contributes to the equitable degrees of two distinct vertices. Thus when the equitable degrees of the vertices are added, each equitable edge is counted exactly two times. Thus the sum of the equitable degrees is twice the equitable size of the graph, that is
be a graph. Then any equitable edge contributes to the equitable degrees of two distinct vertices. Thus when the equitable degrees of the vertices are added, each equitable edge is counted exactly two times. Thus the sum of the equitable degrees is twice the equitable size of the graph, that is .
.
Theorem 2.3. Every graph has an even number of equitable odd vertices.
Proof. Suppose that the sum of the equitable degrees of the equitable odd vertices is  and the sum of the equitable degrees of the equitable even vertices is
and the sum of the equitable degrees of the equitable even vertices is . The number
. The number  is even, and the number
is even, and the number 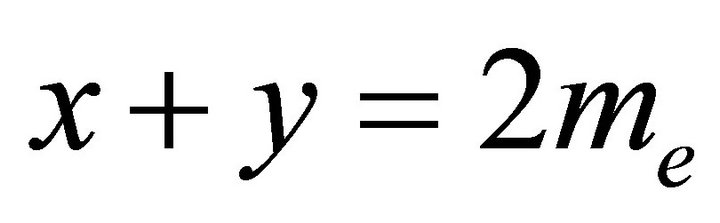 is even. Hence
is even. Hence 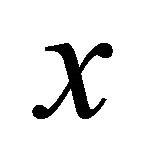 is even. If there are
is even. If there are  equitable odd vertices, the even number
equitable odd vertices, the even number 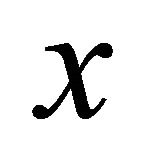 is the sum of
is the sum of  odd numbers. So
odd numbers. So  is even.
is even.
We can define the equitable complete graph  as a connected graph which all its edges are equitable edges. and analogous to the equitable complete graph we can defined the equitable complement graph of a graph
as a connected graph which all its edges are equitable edges. and analogous to the equitable complete graph we can defined the equitable complement graph of a graph  as following:
as following:
Definition 2.4. For any graph , the equitable complement graph of
, the equitable complement graph of  denoted by
denoted by  is the graph with the same vertices as
is the graph with the same vertices as  and any two vertices
and any two vertices  are adjacent if
are adjacent if  and
and 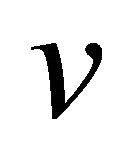 are not equitable adjacent in
are not equitable adjacent in .
.
The relation between the complement of the graph and the equitable complement graph of a graph can be found in the following theorem.
Theorem 2.5. For any graph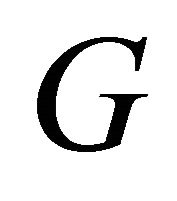 ,
, .
.
Proof. Let  be any edge in
be any edge in . Then
. Then  and
and 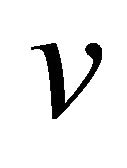 are not-adjacent vertices in
are not-adjacent vertices in , which implies
, which implies 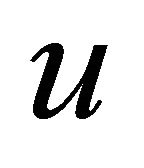 and
and  are not equitable adjacent in
are not equitable adjacent in . Hence
. Hence  is an edge in the graph
is an edge in the graph . Therefore
. Therefore .
.
Theorem 2.6. For any graph  with
with  vertices,
vertices,  if and only if
if and only if  is isomorphic to an equitable complete Graph.
is isomorphic to an equitable complete Graph.
Proof. Let 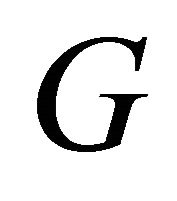 be an equitable complete Graph and let
be an equitable complete Graph and let  be any edge in the graph
be any edge in the graph . Then
. Then  is nonadjacent to
is nonadjacent to  in
in . Hence
. Hence  is an edge in
is an edge in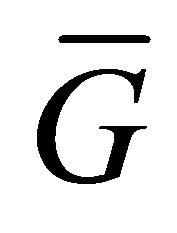 , and since from the previous theorem we have
, and since from the previous theorem we have . Hence
. Hence . Conversely, suppose that
. Conversely, suppose that  and
and  is not an equitable complete graph. Then there exists at least one edge
is not an equitable complete graph. Then there exists at least one edge  in
in  which is not equitable edge. That means
which is not equitable edge. That means  and
and 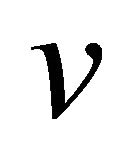 are not equitable adjacent, which implies that
are not equitable adjacent, which implies that  is an edge in
is an edge in . But clearly
. But clearly  and
and  are not adjacent in
are not adjacent in , a contradiction.
, a contradiction.
A graph  is called an equitable edge-free graph if for any two adjacent vertices
is called an equitable edge-free graph if for any two adjacent vertices 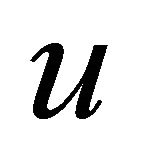 and
and  in
in ,
,
 .
.
Proposition 2.7. For any graph  with
with  vertices,
vertices,  if and only if
if and only if  is an equitable edge-free.
is an equitable edge-free.
Proof. Let 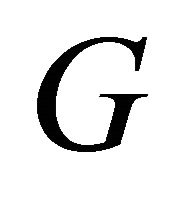 be an equitable edge-free graph with
be an equitable edge-free graph with 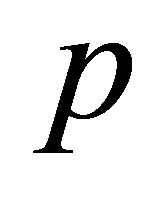 vertices. Then any two vertices in
vertices. Then any two vertices in  are adjacent. Hence
are adjacent. Hence .
.
Conversely, suppose . Hence any two vertices in
. Hence any two vertices in  are adjacent, then
are adjacent, then 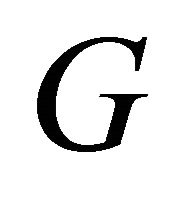 has no any equitable edge. Therefore
has no any equitable edge. Therefore  is equitable edge-free.
is equitable edge-free.
Theorem 2.8. For any graph 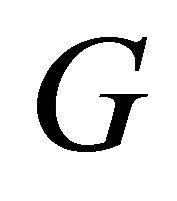 with
with  vertices,
vertices,  if and only if
if and only if 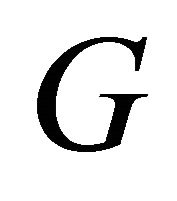 is isomorphic to the complete Graph
is isomorphic to the complete Graph .
.
Proof. Let . Then any two vertices
. Then any two vertices
 are equitable adjacent. Hence
are equitable adjacent. Hence  does not contain any edge. Therefore
does not contain any edge. Therefore .
.
Conversely, suppose that , and if possible
, and if possible  is not complete Graph. This implies that there exist at least two nonadjacent vertices
is not complete Graph. This implies that there exist at least two nonadjacent vertices  and
and 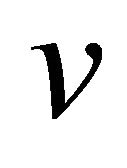 in
in  which are adjacent in
which are adjacent in . Thus
. Thus  and
and  are adjacent in
are adjacent in , a contradiction. Hence
, a contradiction. Hence 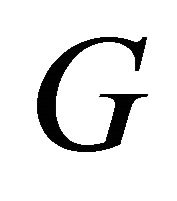 is complete graph
is complete graph .
.
Corollary 2.9. For any equitable edge-free graph 
with  vertices,
vertices,  .
.
Theorem 2.10. Let 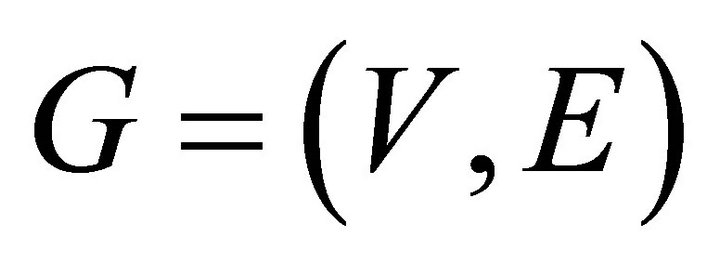 be a graph with p vertices and contains at least one non equitable edge with the property that any two vertices
be a graph with p vertices and contains at least one non equitable edge with the property that any two vertices  in
in , we have
, we have
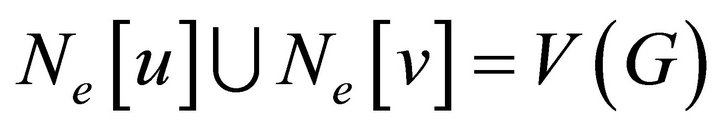 . Then
. Then  .
.
Proof. Let 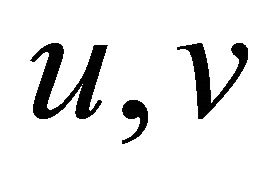 be any two vertices in
be any two vertices in . Then we have two cases:
. Then we have two cases:
Case 1: If  and
and  are adjacent vertices in
are adjacent vertices in , then we have two subcases:
, then we have two subcases:
a) If  is equitable edge, then
is equitable edge, then  and
and  are not adjacent in
are not adjacent in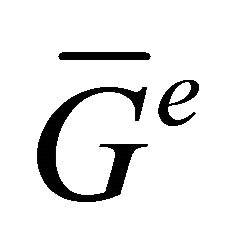 . Thus
. Thus  and
and  are adjacent in
are adjacent in .
.
b) If  is not equitable edge that means
is not equitable edge that means  and since
and since . Then
. Then  and
and  are adjacent but not equitable adjacent in
are adjacent but not equitable adjacent in . Therefore,
. Therefore,  and
and  are adjacent in
are adjacent in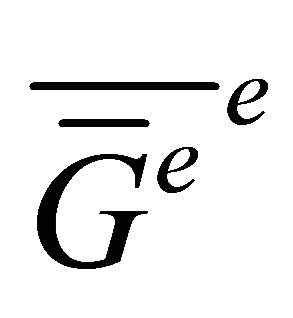 .
.
Case 2: If  and
and  are nonadjacent vertices in
are nonadjacent vertices in , then
, then 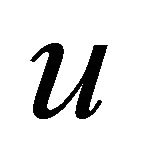 and
and  are adjacent vertices in
are adjacent vertices in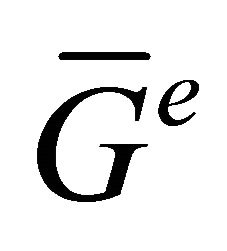 . Since
. Since
 , we get
, we get  and
and  are not equitable adjacent in
are not equitable adjacent in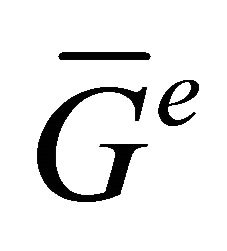 . Hence
. Hence  is adjacent to
is adjacent to  in
in . Therefore any two vertices in
. Therefore any two vertices in  are adjacent. Hence
are adjacent. Hence .
.
3. Equitable Connectivity and Equitable Regularity
A graph  is said to be equitable connected if there is at least one equitable path between every pair of vertices in
is said to be equitable connected if there is at least one equitable path between every pair of vertices in . Otherwise,
. Otherwise,  is equitable disconnected. It is easy to see that an equitable disconnected graph consists of two or more equitable connected graphs. Each of these equitable connected subgraphs is called equitable component. Clearly any equitable connected graph is connected but the converse is not true equitable in general. For example, the graph
is equitable disconnected. It is easy to see that an equitable disconnected graph consists of two or more equitable connected graphs. Each of these equitable connected subgraphs is called equitable component. Clearly any equitable connected graph is connected but the converse is not true equitable in general. For example, the graph , where
, where  is connected but not equitable connected.
is connected but not equitable connected.
Theorem 3.1. The isomorphism between the graphs preserve the number of equitable component.
Proof. Let  and
and  be isomorphic graphs. Let
be isomorphic graphs. Let 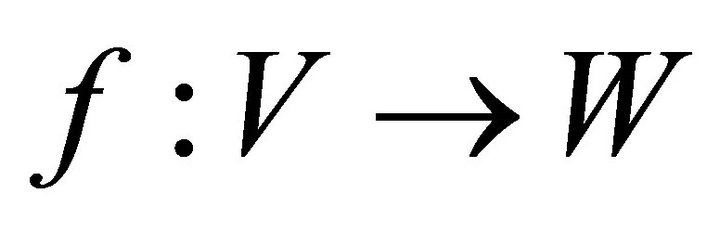 be an isomorphism. If
be an isomorphism. If  is an equitable path in
is an equitable path in  from
from  to
to , then
, then  is an equitable path in
is an equitable path in  from
from  to
to . Thus,
. Thus,  and
and  are in the same equitable component of
are in the same equitable component of  if and only if
if and only if  to
to 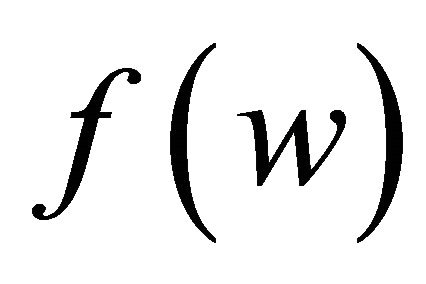 are in the same component of H.
are in the same component of H.
Theorem 3.2. A graph  is equitable disconnected if and only if its vertex set
is equitable disconnected if and only if its vertex set 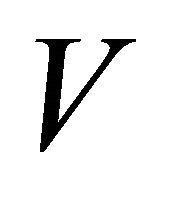 can be partitioned into two nonempty, disjoint subsets
can be partitioned into two nonempty, disjoint subsets  and
and  such that there exists no equitable edge in
such that there exists no equitable edge in  whose one end vertex is in subset
whose one end vertex is in subset  and the other in subset
and the other in subset  .
.
Proof. Suppose that we have the partition of 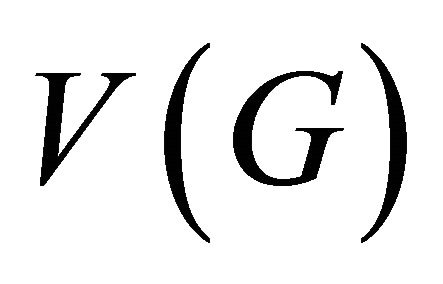 into disjoint subsets
into disjoint subsets  and
and  such that there exists no equitable edge in
such that there exists no equitable edge in  whose one end vertex is in subset
whose one end vertex is in subset  and the other in subset
and the other in subset . Consider two arbitrary vertices
. Consider two arbitrary vertices  and
and  of
of , such that
, such that 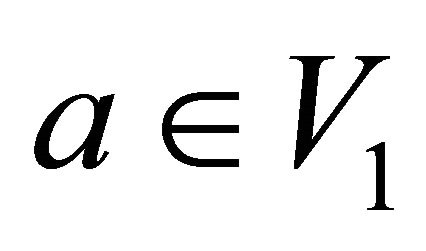 and
and . Then there is no equitable path between the vertices
. Then there is no equitable path between the vertices  and
and . Hence, if a partition exists,
. Hence, if a partition exists,  is not equitable connected.
is not equitable connected.
Conversely, let  be a disconnected graph. Consider
be a disconnected graph. Consider  to be a vertex in
to be a vertex in . Let
. Let  be the set of all vertices that are joined by equitable paths to
be the set of all vertices that are joined by equitable paths to . Since
. Since  is equitable disconnected,
is equitable disconnected,  does not include all vertices of
does not include all vertices of . The remaining vertices will form a (nonempty) set
. The remaining vertices will form a (nonempty) set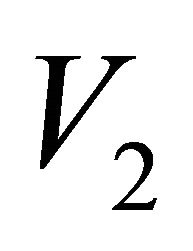 . No vertex in
. No vertex in  is joined to any in
is joined to any in  by an equitable edge. Hence the partition.
by an equitable edge. Hence the partition.
Theorem 3.3. If a graph (equitable connected or equitable disconnected) has exactly two vertices of odd equitable degree, then there exists an equitable path joining these two vertices.
Proof. Let  be a graph with all even vertices except vertices
be a graph with all even vertices except vertices  and
and , which are odd. From Theorem 2.3, no graph can have an odd number of equitable odd vertices. Therefore, in graph
, which are odd. From Theorem 2.3, no graph can have an odd number of equitable odd vertices. Therefore, in graph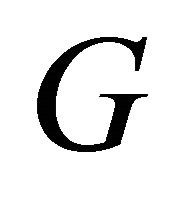 ,
,  and
and 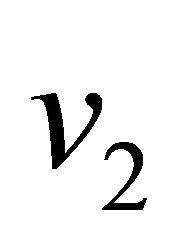 must belong to the same equitable component, and hence must have equitable path between them.
must belong to the same equitable component, and hence must have equitable path between them.
Definition 3.4. Let 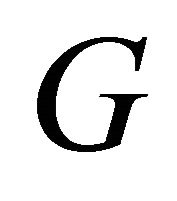 be a graph on
be a graph on  vertices. An equitable disconnecting set of edges is a subset
vertices. An equitable disconnecting set of edges is a subset  such that
such that  is equitable disconnected. The edge equitable connectivity,
is equitable disconnected. The edge equitable connectivity,  , is the smallest number of edges in any equitable disconnecting set.
, is the smallest number of edges in any equitable disconnecting set.
We adopt the convention that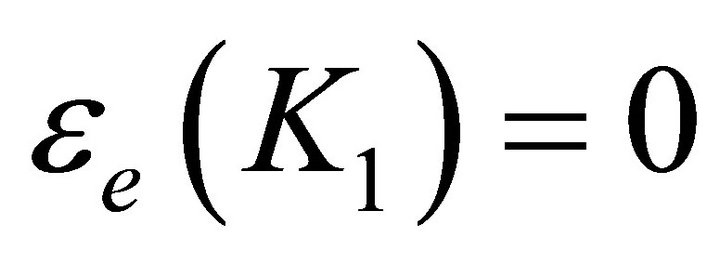 . Thus
. Thus 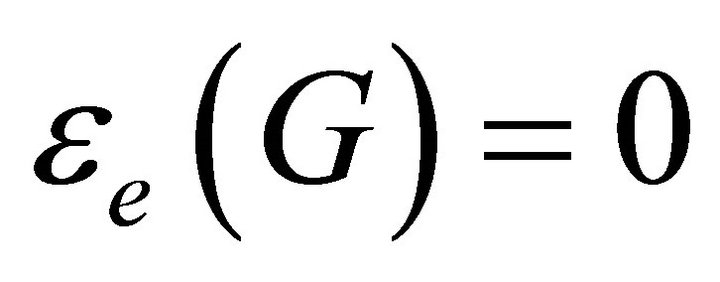 if and only if
if and only if  or
or  is equitable disconnected. If
is equitable disconnected. If  then
then  is a connected graph having an equitable edge
is a connected graph having an equitable edge  such that
such that  is equitable disconnected. An equitable edge whose removal increases the number of equitable components is called equitable cut-edge (equitable bridge) of
is equitable disconnected. An equitable edge whose removal increases the number of equitable components is called equitable cut-edge (equitable bridge) of .
.
Example. In the graph  in Figure 1, the edge (12) is equitable cut edge but not cut edge. So we have
in Figure 1, the edge (12) is equitable cut edge but not cut edge. So we have  but
but .
.
Proposition 3.5. If  is a graph, then
is a graph, then  . That is, the edge equitable connectivity of
. That is, the edge equitable connectivity of  can be no larger than the minimum equitable degree of
can be no larger than the minimum equitable degree of .
.
Proof. let  be an equitable connected graph on
be an equitable connected graph on 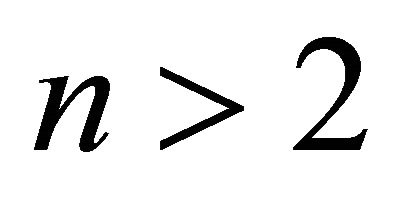 vertices and suppose
vertices and suppose  is a vertex of equitable degree
is a vertex of equitable degree . Since
. Since
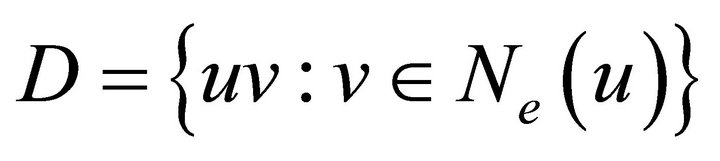 is an equitable disconnecting set of edges,
is an equitable disconnecting set of edges, .
.
The following result is straightforward.
Proposition 3.6. Suppose G is an equitable connected graph. Let  be equitable edge. Then
be equitable edge. Then  is an equitable cut-edge of
is an equitable cut-edge of  if and only if
if and only if  is the only equitable path in
is the only equitable path in 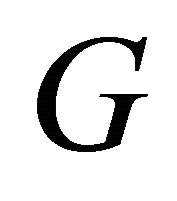 from
from  to
to .
.
Definition 3.7. Let  be an equitable connected graph. An equitable vertex cut (or an equitable separateing set) of
be an equitable connected graph. An equitable vertex cut (or an equitable separateing set) of  is a set
is a set  such that
such that  is equitable disconnected. The connectivity,
is equitable disconnected. The connectivity,  , is the smallest number of vertices in any equitable vertex cut of
, is the smallest number of vertices in any equitable vertex cut of . A vertex whose removal increases the number of equitable components of
. A vertex whose removal increases the number of equitable components of 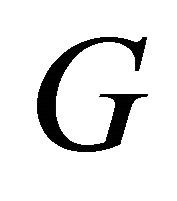 is called equitable cut-vertex (or point of equitable articulation). For the graph in Figure 1,
is called equitable cut-vertex (or point of equitable articulation). For the graph in Figure 1, 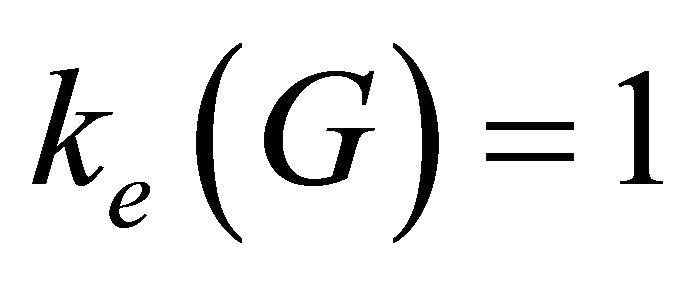 but
but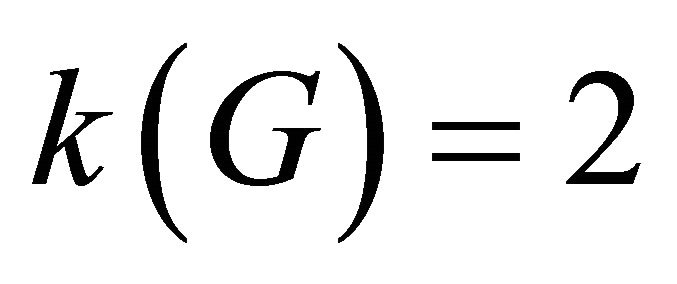 .
.
The maximal equitable connected subgraph of 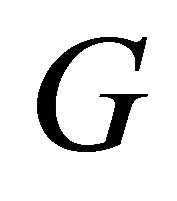 that has no equitable cut-vertex is called an equitable block of
that has no equitable cut-vertex is called an equitable block of .
.
Theorem 3.8. For any graph ,
,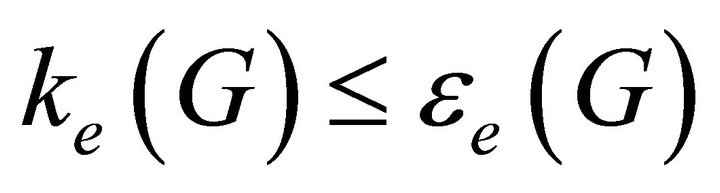 .
.
Proof. If , then
, then  is equitable disconnected and
is equitable disconnected and . If
. If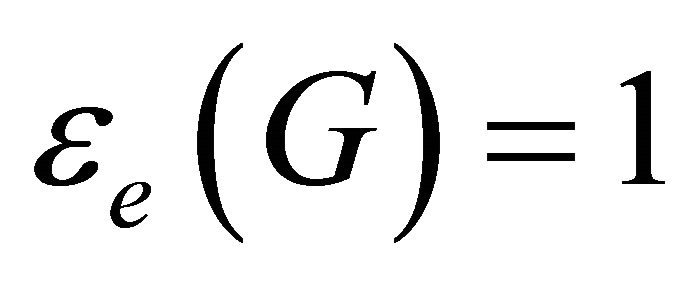 , then this
, then this

Figure 1. Equitable cut edge but not cut edge.
graph is equitable connected with equitable bridge , that means
, that means 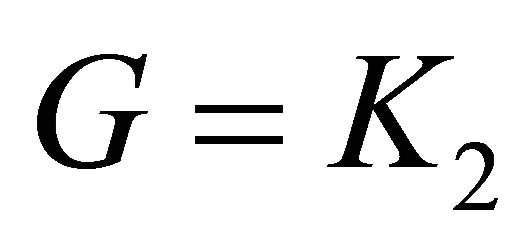 or one of the vertices which incident with
or one of the vertices which incident with  is equitable cut vertex. Therefore,
is equitable cut vertex. Therefore, . If
. If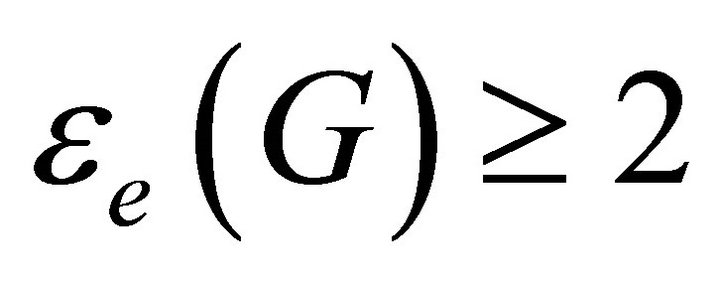 , then removal
, then removal  edges results in equitable disconnected graph, that means the removal
edges results in equitable disconnected graph, that means the removal  of this edges results in a graph
of this edges results in a graph  with an equitable bridge
with an equitable bridge . For each of these
. For each of these  edges select an incident vertex different from
edges select an incident vertex different from 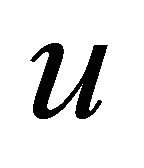 or
or . The removal of these
. The removal of these  vertices remove all the
vertices remove all the 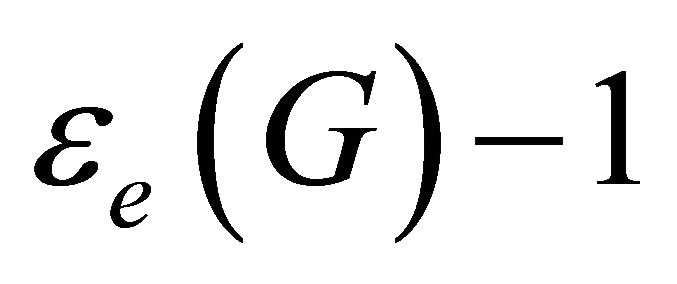 edges. If the resulting graph is disconnected, then
edges. If the resulting graph is disconnected, then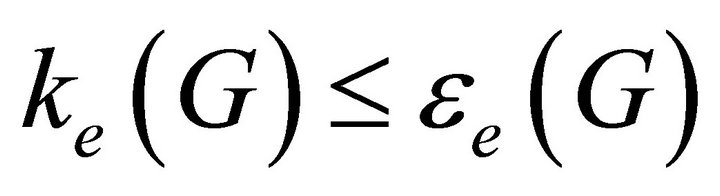 . If not,
. If not,  is equitable bridge of this subgraph and hence the removal of
is equitable bridge of this subgraph and hence the removal of  or
or  results in an equitable disconnected. Hence,
results in an equitable disconnected. Hence, .
.
Definition 3.9. A graph  is called
is called 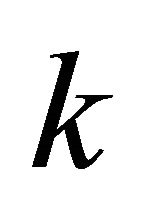 -equitable regular graph if
-equitable regular graph if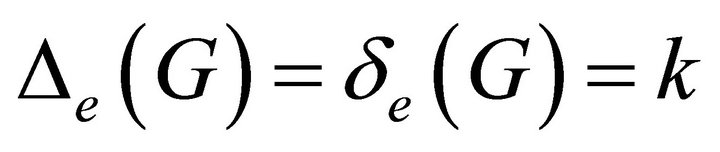 .
.
Observation 3.10. Every 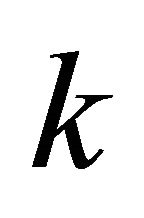 -regular graph is
-regular graph is 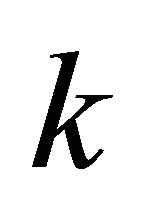 -equitable regular graph but the converse is not true, in general.
-equitable regular graph but the converse is not true, in general.
Example. The graph in the Figure 2 is 2-equitable regular graph but not regular.
4. An Equitable Line Graph and an Equitable Total Graph
Definition 4.1. Given a graph , its equitable line graph
, its equitable line graph  is a graph such that 1) Each vertex of
is a graph such that 1) Each vertex of  represents an equitable edge of
represents an equitable edge of ; and 2) Two vertices of
; and 2) Two vertices of  are adjacent if and only if their corresponding equitable edges share a common endpoint (are adjacent) in
are adjacent if and only if their corresponding equitable edges share a common endpoint (are adjacent) in .
.
Proposition 4.2. The line graph of equitable connected graph is connected.
Proof. If 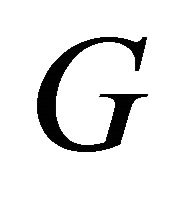 is equitable connected, it contains equitable path connecting any two of its edges, which translates into a path in
is equitable connected, it contains equitable path connecting any two of its edges, which translates into a path in 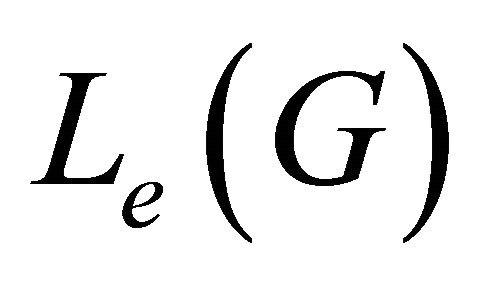 containing any two of the vertices of
containing any two of the vertices of . Hence
. Hence  is connected.
is connected.
Observation 4.3. Let  be any graph. Then
be any graph. Then  .
.
Remark. The equitable line graph of equitable connected graph is connected but not equitable connected in general. In Figure 3, the equitable line graph of equitable connected graph is connected but not equitable connected.

Figure 2. 2-equitable regular graph but not regular.
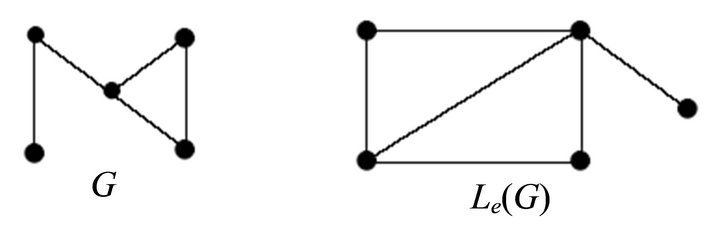
Figure 3. Equitable line graph of equitable connected graph.
Definition 4.4. Let  be a graph. The equitable graph
be a graph. The equitable graph  of
of  is defined as the graph with vertex set
is defined as the graph with vertex set  and two vertices
and two vertices ,
, 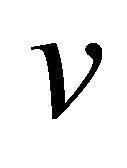 are adjacent if and only if
are adjacent if and only if  and
and  are equitable adjacent in
are equitable adjacent in .
.
The following result is immediate.
Proposition 4.5. For any graph  with at least one equitable edge, the following hold.
with at least one equitable edge, the following hold.
1)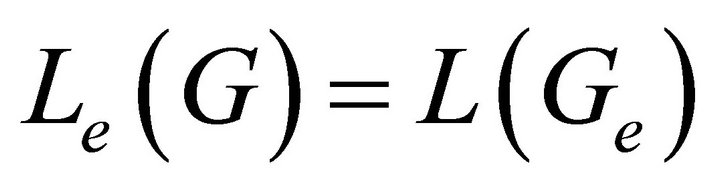 .
.
2)  if and only if
if and only if  is an equitable complete graph.
is an equitable complete graph.
3) If , then
, then  but the converse is not true.
but the converse is not true.
Theorem 4.6. If 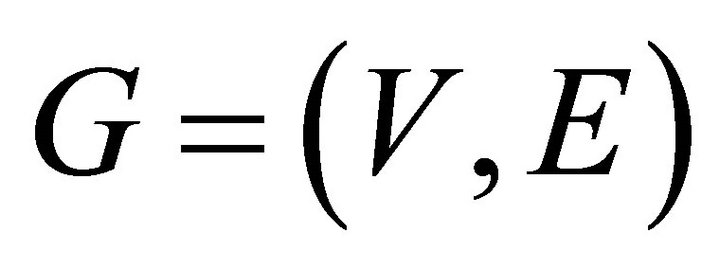 is a graph and
is a graph and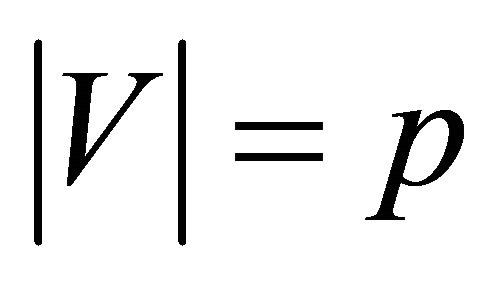 ,
,  whose vertices have equitable degree
whose vertices have equitable degree , then
, then
 has
has  vertices and
vertices and where
where  is the number of equitable edges in
is the number of equitable edges in .
.
Proof. Clearly from the definition of equitable line graph  has
has  vertices the
vertices the  equitable edges incident with a point
equitable edges incident with a point  contribute
contribute  to
to , so
, so

Proposition 4.7. If  is a graph, then
is a graph, then  if and only if
if and only if  is an equitable complete graph.
is an equitable complete graph.
Proof. If  is an equitable complete graph then clearly
is an equitable complete graph then clearly .
.
Conversely, let . Then
. Then  and
and 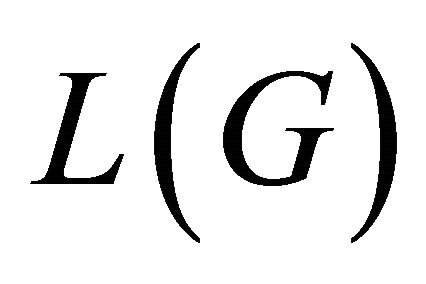 have the same number of vertices that means
have the same number of vertices that means . Hence
. Hence  is an equitable complete graph.
is an equitable complete graph.
Theorem 4.8. A connected graph is isomorphic to its equitable line graph if and only if it is a cycle.
Proof. If 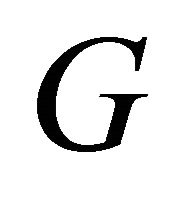 is cycle, then clearly
is cycle, then clearly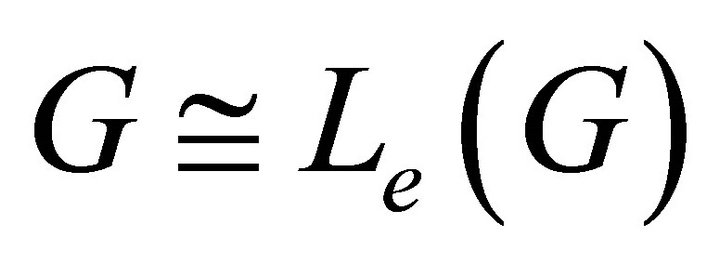 . Conversely, if
. Conversely, if  is isomorphic to
is isomorphic to , that means
, that means  is an equitable complete graph, and by Proposition 4.7.
is an equitable complete graph, and by Proposition 4.7. . Hence
. Hence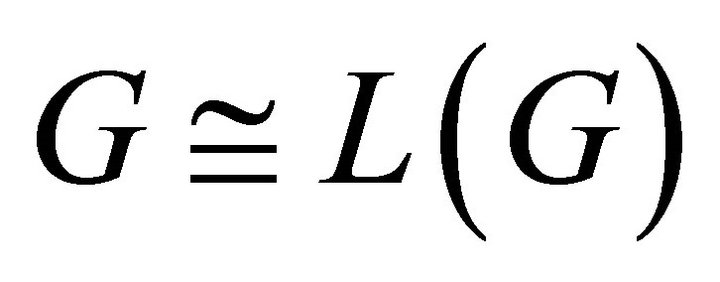 . Therefore
. Therefore  is cycle.
is cycle.
Definition 4.9. The equitable total graph  of a graph
of a graph 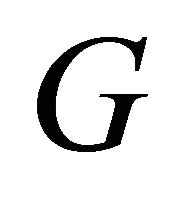 is a graph such that 1) The vertex set of
is a graph such that 1) The vertex set of  corresponds to the vertices and equitable edges of
corresponds to the vertices and equitable edges of  and 2) Two vertices are adjacent in
and 2) Two vertices are adjacent in  if and only if their corresponding elements are either adjacent or incident in
if and only if their corresponding elements are either adjacent or incident in .
.
Observation 4.10. For any graph  the equitable total graph is a subgraph of the total graph of a graph
the equitable total graph is a subgraph of the total graph of a graph .
.
Proposition 4.11. If  is a vertex and
is a vertex and 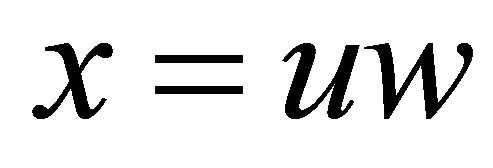 be equitable edge in a graph
be equitable edge in a graph , then the degree of the vertex
, then the degree of the vertex  is
is 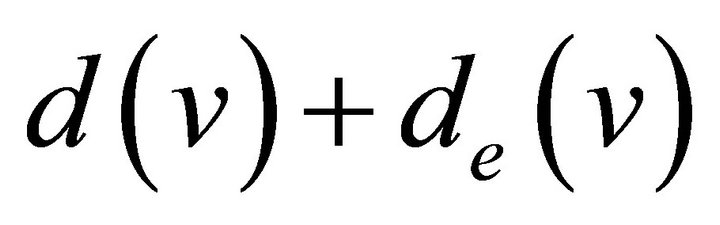 and the degree of
and the degree of  is
is  in
in .
.
Proposition 4.12. If  is a graph with
is a graph with  vertices and
vertices and  edges and its vertices have equitable degree
edges and its vertices have equitable degree , then
, then  has
has  vertices and
vertices and
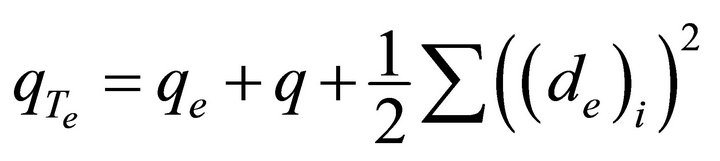 where
where  is the number of equitable edges in
is the number of equitable edges in .
.
Proof. The number of vertices of the graph  is the sum of number of equitable edge and number of vertices in
is the sum of number of equitable edge and number of vertices in , that is
, that is  has
has  vertices. By the definition of total graph of
vertices. By the definition of total graph of , the number of edges in
, the number of edges in  is the sum of edges in
is the sum of edges in  and the number of edges in the equitable line graph of
and the number of edges in the equitable line graph of  and twice the number equitable edges in
and twice the number equitable edges in , that is;
, that is;
 . Hence,
. Hence,  .
.