1. Introduction
In machine learning, the models quality depends much on features used. Often, one faces problems of lacking useful features and/or of redundant features, causing poor modeling and prediction performance. For better modeling, we need to include high predictive capability features and exclude low predictive capability or redundant features from the original group of features. Good feature selection can increase the modeling efficiency and is the prerequisite for subsequent works. Hence, identifying a series of representative features has become a central problem. In general, features reduction, consists of feature selection [1] and feature extraction [2]. The former one tries to find a subset which fit the model best from original features set, while the latter one attempts to transform the original high dimension features space into a low one. The features selection can be further divided into two categories: filters [2] and wrappers [3].
Time series [4] is a collection of observations taken sequentially in time, and occurs in many fields, e.g. the stock price in successive minutes [5], the indoor temperature in successive hours, etc. In this paper, we address feature selection for time series. To this end, many methods of feature selection have been reported in the literature. However, none of them can always produce the good performance. In this regard, we first conduct comparative study of several typical correlation based methods of feature selection, and find that they do not work well for time series though they can work well for static systems. This motivates us to provide better schemes for feature selection. Then, theoretical analysis for linear time series is carried out to show why they fail. Based on these observations, we propose a new correlation-based feature selection method. Our main idea is that the features highly correlated with progressive response while lowly correlated with other features should be selected, and for groups of selected features with similar residuals, the one with a smaller number of features should be selected. For linear and nonlinear time series, the proposed method yields high accuracy in both feature selection and feature rejection.
The rest of this paper is organized as follows. The feature selection methods are presented in Section 2. In Section 3, we describe the data sets obtained and simulation designs. The results and discussions are given in Section 4. Finally, conclusions are drawn in Section 5.
2. Feature Selection
2.1. Linear Regression Method
In linear regression method [6], suppose that the response  is related to the feature
is related to the feature  in a linear fashion,
in a linear fashion,
 (1)
(1)
where  are m random variables with uniform distribution on interval
are m random variables with uniform distribution on interval , independent of each other, and added into
, independent of each other, and added into  to test for effectiveness of this feature selection method. These equations for all
to test for effectiveness of this feature selection method. These equations for all  are integrated to form the matrix equation,
are integrated to form the matrix equation,
 (2)
(2)
where
 (3)
(3)
 (4)
(4)
 (5)
(5)
It is solved by the linear least squares method [7] to find weights . We find the maximum absolute value of last
. We find the maximum absolute value of last  weights,
weights,
 (6)
(6)
The feature  is retained in the selected feature group if
is retained in the selected feature group if , or discarded otherwise.
, or discarded otherwise.
2.2. Linear Correlation Method
Pearson product-moment correlation coefficient [8] is a measure of the linear dependence of two variables  and
and , giving a value between −1 and 1 inclusive. It is usually estimated by
, giving a value between −1 and 1 inclusive. It is usually estimated by
 (7)
(7)
based on a sample of paired data . Similarly to the linear regression method, we add m random variables with uniform distribution on interval
. Similarly to the linear regression method, we add m random variables with uniform distribution on interval , independent of each other, and added into
, independent of each other, and added into  to test for effectiveness of this feature selection method. Linear correlation coefficients
to test for effectiveness of this feature selection method. Linear correlation coefficients  between response
between response  and each feature
and each feature  are calculated, and the maximum absolute value of the last
are calculated, and the maximum absolute value of the last  ones is determined,
ones is determined,
 (8)
(8)
The feature  is retained in the selected feature group if
is retained in the selected feature group if , i.e.
, i.e.  is more correlated to the response than the random variables. Otherwise,
is more correlated to the response than the random variables. Otherwise,  is discarded.
is discarded.
2.3. Spearsmans Correlation Method
It is well known that the relationships between features and the response could be nonlinear. The linear correlation coefficient captures the linear relation only, and thus is not accurate in the nonlinear case, which calls for nonlinear correlation coefficient method. The simplest nonlinear correlation coefficient is the Spearmans rank correlation coefficient, and it is more appropriate when the data points seem to follow a curve instead of a straight line, and is less sensitive to the effects of outliers. Spearmans rank correlation coefficient is a measure of statistical dependence between 2 variables, and is defined as the Pearson correlation coefficient between the ranked variables [9]. Given  raw data points
raw data points ,
,  are ranked with
are ranked with  such that the largest value has rank 1, the second largest value rank 2, etc. whereas
such that the largest value has rank 1, the second largest value rank 2, etc. whereas  are similarly ranked with
are similarly ranked with . Spearmans rank correlation coefficient of
. Spearmans rank correlation coefficient of  and
and  is Pearson correlation coefficient calculated from
is Pearson correlation coefficient calculated from  and
and . The efficient way to calculate Spearmans rank correlation coefficient is to use
. The efficient way to calculate Spearmans rank correlation coefficient is to use
 (9)
(9)
The feature selection based Spearmans rank correlation coefficient follows its linear counterpart by replacing the linear correlation coefficients by Spearmans rank correlation coefficient.
2.4. Local Learning Method
A new algorithm, called “Local Learning Based Feature Selection for High Dimensional Data Analysis of feature selection”, was proposed by Sun et al. [10]. Its core idea is that an arbitrarily complicated nonlinear problem can be decomposed into a series of local linear problems based on local learning and then the feature relevance is learned globally. Their method does not make any assumption on the data distribution, and is capable of selecting useful features successfully from a large number of features that are irrelevant. Its flowchart is shown as follows.
Input: Data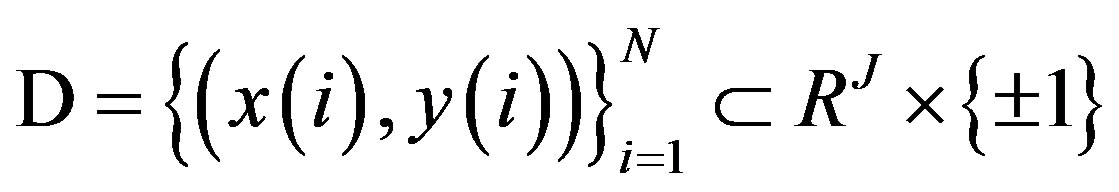 , kernel width
, kernel width , regulation parameter
, regulation parameter , stop criterion
, stop criterion .
.
Output: Feature weights .
.
1. Initiation: Set 
2. Repeat:
a) Compute 
b) Compute  and
and  with equations,
with equations,

and

c) Solve for  through gradient descent using the update rule,
through gradient descent using the update rule,

d) 
3. Until: 
4. 
In this algorithm,  is the feature vector,
is the feature vector,  is the label corresponding to
is the label corresponding to , and d() stands for the Manhattan distance of
, and d() stands for the Manhattan distance of ,
,  .
.
 (10)
(10)
2.5. 2D-Correlation Method
The correlation methods mentioned above only consider correlation from features to response. It tends to select redundant features if these features are all highly related to response but they are mutually correlated too. To select a set of features as good and few as possible for learning task, one must take into consideration possible interdependencies between the features as well. As a trade-off between the complexity of the selection process and the quality of the selected feature set, a pair wise selection strategy has been recently suggested [11]. This method assumes that a feature is irrelevant if it is uncorrelated with response, otherwise it is useful, and the feature is redundant if a feature is highly correlated with other features.
In this paper, we propose some modifications. Firstly, we use the rank correlation coefficient instead as it can capture nonlinear relation and is computational efficient. Secondly, we compare correlation from real features with those from pure noises, and retain those features only when they are more relevant than noises. Thirdly, we introduce tuning parameters to allow the users to fit to specific situations. Thus, the main idea of this modified method is to check first whether the features are correlated in linear or nonlinear way to each other. If the correlation coefficients between a feature and other features exceed the correlation coefficient between this feature and response by some extent, it means that this feature is not useful, and its information can be gained from high correlated other features. The detailed procedure is as follows1. Initialization:
a) Define the feature sets: Set  as the original set of
as the original set of  features and the selected feature set
features and the selected feature set  as empty set.
as empty set.
b) Select the first feature: compute the rank correlation coefficient  between the feature
between the feature  and the response
and the response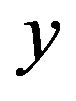 . Then include the feature with the largest
. Then include the feature with the largest  as the first selected feature in
as the first selected feature in  and exclude it from
and exclude it from .
.
c) Remove noisy features: compute the rank correlation coefficient  between noise
between noise  and the response y, where
and the response y, where . Set the default m as 20. Let the standard deviation of these m coefficients be
. Set the default m as 20. Let the standard deviation of these m coefficients be . Take
. Take  away from
away from , if
, if  be in
be in  such that
such that , where
, where  is the threshold ratio.
is the threshold ratio.
2. Search for relevant features, repeat until no feature is produced from (b) below.
a) Compute the rank correlation coefficient  for each pair of variables
for each pair of variables  with
with  and
and .
.
b) Select the next feature: choose feature  as the one that maximizes
as the one that maximizes , subject to
, subject to , where
, where  is the threshold ratio. Move
is the threshold ratio. Move  from
from  into
into .
.
3. Output the set  as the selected features.
as the selected features.
It will be seen from our simulation study below that correlation based methods work badly for time series in general. The best one, the 2D-correlation method, is able to reject irrelevant features but unable to select minimum number of relevant features. We will find causes of their failure through theoretical analysis in the next section.
3. Theoretical Analysis and Progressive Correlation Method
Consider autoregressive process  with order
with order , which is described by
, which is described by
 (11)
(11)
where  is a purely random process with zero mean and variance
is a purely random process with zero mean and variance . Assume this process is stationary. Then multiply through (11) by
. Assume this process is stationary. Then multiply through (11) by , take expectations, and divide
, take expectations, and divide  to get
to get
 (12)
(12)
where  is the correlation coefficients of
is the correlation coefficients of  and
and  [4]. This holds true, independent of the initial condition and variance of
[4]. This holds true, independent of the initial condition and variance of . For
. For , (12) becomes
, (12) becomes
 (13)
(13)
It is shown in Figure 1 for 
 .
.
If the 2D-correlation method is applied to the above case, we find that there is low efficiency in selecting useful features. Suppose that the feature with time lag 1,  , is selected, features with time lags 2,
, is selected, features with time lags 2,  , and 3,
, and 3,  , should be considered in the subsequent steps. For system in (11) with
, should be considered in the subsequent steps. For system in (11) with , it follows from (13) and Figure 1 that features,
, it follows from (13) and Figure 1 that features,  and
and , have higher correlation with selected feature,
, have higher correlation with selected feature, 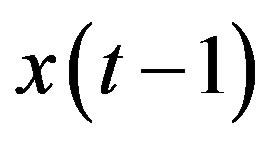 , than that with response,
, than that with response,  , and thus are not selected. In general, it is observed that though
, and thus are not selected. In general, it is observed that though , are redundant, each of them have significant correlation with response and their values are not necessarily smaller than
, are redundant, each of them have significant correlation with response and their values are not necessarily smaller than

Figure 1. Correlation coefficient for p = 3.
those of . Besides, they are not necessarily smaller than their own mutual correlations. Thus, the methods mentioned above fail in general.
. Besides, they are not necessarily smaller than their own mutual correlations. Thus, the methods mentioned above fail in general.
To overcome the drawbacks in the above correlation methods, we propose the progressive correlation method as follows. Select , if correlation of
, if correlation of  and
and  decreases significantly with that of
decreases significantly with that of  and y, no longer solely based on single correlation of
and y, no longer solely based on single correlation of  with y. Further, we also use the correlation of
with y. Further, we also use the correlation of  with
with  when we consider
when we consider  after
after  is selected. In this new method, we favor the feature with least time lags when several features with similar relative correlation coefficients exist. And if several groups of selected features have similar modeling residuals, we favor the one with a smaller number of features. The detailed procedure is as follows1. Initialization:
is selected. In this new method, we favor the feature with least time lags when several features with similar relative correlation coefficients exist. And if several groups of selected features have similar modeling residuals, we favor the one with a smaller number of features. The detailed procedure is as follows1. Initialization:
a) Define the feature sets: Set  as the original set of
as the original set of  features and the selected feature set
features and the selected feature set  as empty set.
as empty set.
b) Select the first feature: compute the rank correlation coefficient  between the feature
between the feature  and response
and response . Then find the features which satisfy
. Then find the features which satisfy
 and select among themone with the least time lag. Include it in
and select among themone with the least time lag. Include it in  and exclude it from
and exclude it from .
.
c) Remove noisy features: compute the rank correlation coefficient  between noise
between noise  and the response
and the response , where
, where . Set the default
. Set the default  as 20. Let the standard deviation of these
as 20. Let the standard deviation of these  coefficients be
coefficients be . Let
. Let  in
in  be such that
be such that , where
, where  is the threshold ratio. Take
is the threshold ratio. Take  away from
away from .
.
2. Select feature progressively, repeat until the root mean square error of modelled system stops decreasing or there is no feature in :
:
a) Learn a model with the selected features and response, and calculate the model residual series .
.
b) Calculate rank correlation coefficients  with
with . Then calculate relative correlation coefficients with
. Then calculate relative correlation coefficients with
 .
.
c) Select the feature  which satisfies
which satisfies
 with minimal time lag from response as the new selected feature in
with minimal time lag from response as the new selected feature in  and exclude it from
and exclude it from .
.
d) Update the response with the model residual .
.
3. Varying  to different values, and redo step 1. and 2., several groups of features are selected. For those have similar small modelling residuals, we select the one with smaller number of features and less time lag as final selected features.
to different values, and redo step 1. and 2., several groups of features are selected. For those have similar small modelling residuals, we select the one with smaller number of features and less time lag as final selected features.
4. Output the set  as the selected features.
as the selected features.
4. Simulation Data and Design
For testing feature selection on time series, we construct two dynamic systems. The first one is linear system and described by
 (14)
(14)
where  is white noise with uniform distribution on interval
is white noise with uniform distribution on interval . Coefficients are set as
. Coefficients are set as 

 , and the initial conditions are set to be
, and the initial conditions are set to be . Then the equation gives us a stable system and the response is shown in Figure 2.
. Then the equation gives us a stable system and the response is shown in Figure 2.
The second system is nonlinear and described by
 (15)
(15)
where  is white noise with uniform distribution on interval
is white noise with uniform distribution on interval . At last, we set
. At last, we set 
 and the initial conditions are set to be
and the initial conditions are set to be 
 . Its response is shown in Figure 3. The model without the last three terms in the right hand side is cited from [12], which represents some economic model with cycles.
. Its response is shown in Figure 3. The model without the last three terms in the right hand side is cited from [12], which represents some economic model with cycles.
As our objective is to predict the system response change based on the past observations, we form the features  as
as
 (16)
(16)
and the response  for regression as
for regression as
 (17)
(17)
For classification, we define the label for each feature vector from its corresponding response as follows (0% threshold)
 (18)
(18)
The data set for learning is thus formed by
 with the data
with the data
size equal to .
.
Sometimes, one may be interested in large changes only. Then, one can filter the response with some threshold : a data point in the original data set is kept in the filtered data set for regression if
: a data point in the original data set is kept in the filtered data set for regression if  . The other data points are discarded. The size of the filtered data set will thus be usually reduced, depending on the actual response. The filtered data set for classification is obtained by using the same label definition before.
. The other data points are discarded. The size of the filtered data set will thus be usually reduced, depending on the actual response. The filtered data set for classification is obtained by using the same label definition before.
Equations (16) to (18) are used to generate the following data sets for both linear and nonlinear systems labeled by
| r = 2, 4, 8, 10 |
d = 0, 0.01 |
| m = 0, 3 |
b = 0.01, 0.1, 1 |
The Noise-to-Signal Ratio (NSR) is obtained by
 (19)
(19)
5. Simulation Results
In this section, we first the simulation results for 4 existing methods, respectively, and make a comparison. Then, we present results of the proposed methods (2DCorrelation Method and Progressive Correlation Method).
5.1. Comparison of First Four Methods
Comparisons are made firstly based on the performance for different values of the magnitude of random variables added . After that, normalization is applied to both the feature and response, and performances of the first four methods are then compared in Table 1 to Table 9, respectively.
. After that, normalization is applied to both the feature and response, and performances of the first four methods are then compared in Table 1 to Table 9, respectively.
From the results above, we can conclude that the magnitude of random variables added does not have any significant effect on the performance of the 4 methods: linear regression, linear correlation coefficient, rank correlation coefficient, and local learning method. There are some cases when the performance is affected, for example when Spearmans rank correlation method was applied to nonlinear system with NSR = 0.5224 and r = 10, d = 0.01, m = 3, the rejection rate for b = 0.01 is 0.83, for b = 0.1 is 0.67, and for b = 1 is 1. However, in the majority of the cases, the rejection rate and selection rate are about the same. This might be because the random features which were added do not have any correlation with the response, and thus their correlation coefficient with respect to the response is close to 0. When the magnitude of random variables is increased, the correlation coefficient might be increased, but the change is not very big due to the random nature of these variables. Therefore, the threshold level might not have increased by so much, and the performance level is roughly the same.
Overall, Dr. Suns method of feature selection based on local learning seems to give the best result. In most cases, it is able to remove at least some, if not the majority of the irrelevant features. However, not all of the relevant features were selected; and it fails altogether in a few cases. Nevertheless, it still gives better result than linear correlation coefficient, rank correlation coefficient, and linear regression, which tends to select most of the features, regardless of whether they are relevant.
5.2. 2D-Correlation Method
In the simulation of correlation method, we set the threshold  as 1.5 and the parameter
as 1.5 and the parameter  as 0.5. In our experiments, it indicates that the magnitude of added random variables do not affect the performance significantly, and is set as fixed one [−1, 1]. The simulation results are shown in Tables 10 and 11.
as 0.5. In our experiments, it indicates that the magnitude of added random variables do not affect the performance significantly, and is set as fixed one [−1, 1]. The simulation results are shown in Tables 10 and 11.
In terms of feature rejection, we observe that the correlation method yields quite positive results. In most of the cases, this method is able to eliminate most of the irre-

Table 1. Performance when b = 0.01 (Part 1).

Table 2. Performance when b = 0.01 (Part 2).

Table 3. Performance when b = 0.01 (Part 3).

Table 4. Performance when b = 0.1 (Part 1).

Table 5. Performance when b = 0.1 (Part 2).

Table 6. Performance when b = 0.1 (Part 3).

Table 7. Performance when b = 1 (Part 1).

Table 8. Performance when b = 1 (Part 2).

Table 9. Performance when b = 1 (Part 3).

Table 10. Performance of 2D-correlation method (Part 1).

Table 11. Performance of 2D-correlation method (Part 2).
levant features, with the rate of correctly rejected features almost always higher than 0.5. In some particular situations, the rate of correctly rejected feature stands at 1. This might be because by evaluating the correction coefficient between features, we are able to reduce the number of features that are highly-correlated to each other, and thus feature rejection rate increases. However, there are cases (such as linear data set NSR = 0.8649 with number of features , and the feature threshold level
, and the feature threshold level ) where correct rejection rate is 0. This might be because
) where correct rejection rate is 0. This might be because  is the only irrelevant feature for linear data set, and the number of features were not large enough for the covariance checking to be effective, and hence this irrelevant feature has passed the testing criteria.
is the only irrelevant feature for linear data set, and the number of features were not large enough for the covariance checking to be effective, and hence this irrelevant feature has passed the testing criteria.
In terms of feature selection, this method does not give very good results, especially for linear data sets. For most of the test cases for linear data sets, the method is able to select at most 1 feature out of 2 (if ) or 3 (if
) or 3 (if ). One possible explanation might be the high correlation coefficient between consecutive feature features. For example,
). One possible explanation might be the high correlation coefficient between consecutive feature features. For example, 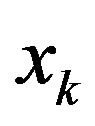 and
and  are consecutive terms in the time series, and hence they are highly correlated. As a result, their correlation coefficient is often higher than the correlation coefficient between the response and feature vector
are consecutive terms in the time series, and hence they are highly correlated. As a result, their correlation coefficient is often higher than the correlation coefficient between the response and feature vector . This weakness should be considered and improve in the extended method.
. This weakness should be considered and improve in the extended method.
5.3. Progressive Correlation Method
In the simulation of progressive correlation method, we change the response to
 (20)
(20)
As both responses come from the same time series, they can be transformed to each other, and either one can be used for feature selection. The threshold  is set as 0.1 - 0.8 with step of 0.1, which can give us eight candidate options, and the parameter
is set as 0.1 - 0.8 with step of 0.1, which can give us eight candidate options, and the parameter  as 5, which can neglect most noise features. Then we select the final selected features from eight candidate options, and choose the option with smaller response residuals, less number of features as the final selection result. The simulation result is shown in Table 12. From the simulation result, we find this kind of feature selection method yields quite good both in feature selection and feature rejection for
as 5, which can neglect most noise features. Then we select the final selected features from eight candidate options, and choose the option with smaller response residuals, less number of features as the final selection result. The simulation result is shown in Table 12. From the simulation result, we find this kind of feature selection method yields quite good both in feature selection and feature rejection for

Table 12. Performance of progressive correlation method.
data sets with and without noise.
For linear data set, the progressive correlation method can accurately select most useful features and reject most irrelevant features for data set without noise. For data set with noise, this method performs better, as it can accurately select all the useful features and rejects most irrelevant features.
For nonlinear data set, the progressive correlation method also achieves better results than before. From the result, it can select most useful features and reject most irrelevant features for data sets with no or low NSR. For data set with high noise, it performs a bit worse. But it still can select some useful features and reject all the irrelevant features.
6. Conclusion
This paper has conducted comparative studies of several representative methods for feature selection in the context of time series modeling. A modified correlation method is presented. In most of the cases, this method is able to eliminate most of the irrelevant features. However, it has a poor performance in feature selection, which can only select half of useful features or even less. We show why these methods fail. In order to rectify the causes of failure, we propose the progressive correlation method. It yields the best results, as generally it can remove most irrelevant features and keep most of the relevant features. Further, it works quite consistently in both linear and nonlinear data sets, and over both high and low noisesignal ratio, indicating that it is a robust method, and can work in different conditions. The use of correlation coefficients patterns shown in formula (12) and Figure 1 to select exact number of features is under progress of our research.
NOTES
*This research is funded by the Republic of Singapores National Research Foundation through a grant to the Berkeley Education Alliance for Research in Singapore (BEARS) for the Singapore-Berkeley Building Efficiency and Sustainability in the Tropics (SinBerBEST) Program. BEARS has been established by the University of California, Berkeley as a center for intellectual excellence in research and education in Singapore.