Solving the Carbon Dioxide Emission Estimation Problem: An Artificial Neural Network Model ()
1. Introduction
Forecasting the future events is a great, important and risky task that attracted many researchers in different fields. This type of problems contains many variables that should be studied, highlighted, and considered to build the suitable models. The world events and processes should be clearly explained and obviously stated to be processed. Climate pollution due to the carbon emission became an important and serious problem that affects the countries from the different aspects, health, climate, agriculture, economics, and tourism. Adjusting the energy policies is a necessary process to void pollution problem, and keeping the atmosphere clear and clean [1]. All the future reading indicates the increase in CO2 and greenhouse gas emission [2]. Many countries today have commitments between them to reduce the greenhouse gas emission, like the Kyoto protocol and the United Nations (UN) agreement to keep checking the CO2 emission percentage in the atmosphere in order to reduce it to the desired levels [3]. Many scientists consider the global warming due to CO2 emission is dangerous and threat the world more than terrorism. Many countries such as the UK Government’s stated a clear objective in order to reduce the CO2 emissions by 10% from the 1990 base by 2010 and in parallel to generate 10% of the UK’s electricity from renewable sources by 2010. Renewable electricity has become equal with CO2 reduction [4]. Several studies were developed to find out the relationship between the different energy consumption and CO2 emission [5,6]. For all that there is a need to develop a non linear model that estimates the carbon dioxide emission. In this paper we used the artificial neural network as a powerful, capable tool in handling such type of modeling process. ANN was largely used in solving different problems in numerous fields such as Rainfall-runoff, water quality, sedimentation and rainfall forecasting. ANN also proved its efficiency and strength in different number of applications [7,8] such as sales prediction [9], shift failures [10], estimating prices [11] and stock returns [12]. In our case we explored the effect of four inputs variables the global oil, natural gas (NG), coal, and primary energy (PE) consumption on the CO2 emission estimation.
2. ANN Back Propagation Algorithm
Artificial Neural Network (ANN) main work is to process the information supplied to the network. It consists of a number of neurons distributed in different layers, these neurons learns by example and trials, the network work according to that and change its weight several times reaching to the optimal weights numbers and values, reaching to the desired output from the given desired input. ANNs simulate the human biological nervous systems, and the way it works is similar to the way the brain process information [13]. ANNs proved its strength and efficiency in solving numerous problems in different world fields such as business [14], forecasting [15], feature extraction [16], classifications [17,18] etc. In this paper, we used the Back-propagation Neural Networks, which is the most popular and the well-known neural type [19,20]. Usually the ANNs architecture consists of three layers, the input layer, hidden layer and the output layer. The input layer receives the input from the outside world, where it has a number of neuron equal to the number of model input. The next layer is called the hidden layer. This layer receives the input from the direct prior layers. The last layer is the output layer, used to produce the output as its name. Neurons in the same layer are not connected to each other but the neurons in each layer were fully connected to all neurons in the next layer. The neurons weights were adjusted using the activation (i.e. sigmoid) function argument. This activation function is assumed to be nonlinear [21]. Let n1(p), n2(p), ···, nn(p) be the network inputs, and let md,1(p), md,2(p),···, md,n (p) be the estimated output. The back propagation neural network function can be also explained as [13].
1) The output from the hidden layer is calculated using Equation (1).
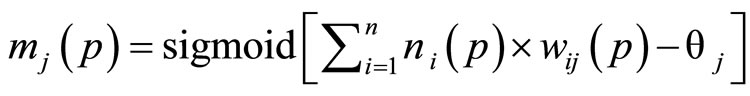 (1)
(1)
Where wij are the weights between the input layer and the hidden layer and between the hidden layer and the output layer, is a threshold value.
The sigmoid function is presented in Equation (2).
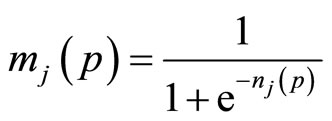 (2)
(2)
The output from the output layer is calculated using Equation (3).
 (3)
(3)
The Error Gradient from the output layer is calculated from Equation (4).
 (4)
(4)
where ek(p) is the error at the output layer
 (5)
(5)
2) The ANNs weight can be computed as given in Equation (6).

 (6)
(6)
To readjust the weights of the ANNs we use Equation (7).
 (7)
(7)
The gradient error in the hidden layer is calculated from Equation (8).
 (8)
(8)
3) Calculating the weights again from Equation (9).
 (9)
(9)
4) A gain we readjust the weights by Equation (10).
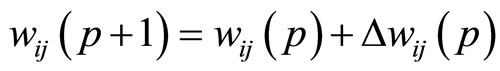 (10)
(10)
The back propagation algorithm can be simply explained and shown from the flow chart in Figure 1.
3. Neural Network Model for Carbon Emission Estimation Problem
The neural network structure that used for the carbon estimation is a multi-layer feed forward network. As explained before the network consists of an input layer, one hidden layer, and an output layer. The input layer consists of four inputs data the global oil, natural gas, coal, and primary energy consumption. The hidden layer function is a nonlinear and consists of 5 neurons. The hidden units

Figure 1. Back propagation flow network diagram.
are fully mapped and connected to both the input and output. The activation function of the hidden units provides the network nonlinearity. The neurons optimal number of the hidden layer was selected by several trials. The network was trained using the Back Propagation (BP) algorithm. The number of neurons in hidden layer is selected to be 5. The output layer consists of one output neuron producing the corresponding carbon emission estimation. The output layer node has a linear activation function. The ANN developed models is shown in Figure 2.
4. Proposed Model Structure and Evaluation Criterion
In our case we used four inputs to estimate the CO2 emission. The inputs are: Oil (t-1), Oil (t-2), NG (t-1), NG (t-2), Coal (t-1), Coal (t-2), PE (t-1), PE (t-2) and the output is the CO2 (t), where the inputs are measured in (Mote) and the output is measured in (Mt). The proposed network architecture was able to produce a very excellent estimation results in both training and testing cases with a very small number of differences. The neural network has 5 neurons in the hidden layers and one neuron in the output layer. The values of global oil, natural gas, coal, and primary energy consumption were obtained from [5,22]. The data in Table 1 were trained from the year 1982 to year 2000, and tested for the year 2003 to year 2010. In this paper we used different validation criterion to find out the percentage of error difference between the actual and estimated values as shown in Equations (11)- (13).
Manhattan distance
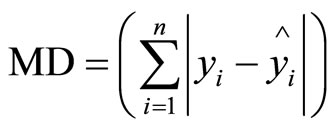 (11)
(11)
Euclidian distance
 (12)
(12)
Mean magnitude of relative error
 (13)
(13)
where y and 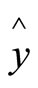 are the actual and estimated values based on the proposed model and N is the number of measurements used in the experiment, respectively. The neural network back propagation learning algorithm was able to perform the task properly by propagating the error each time reaching to the minimum error difference between the actual and the estimated values. In Figure 3, we show The ANN convergence curve. Figure 4 shows the actual and estimated values in both training and testing cases. The actual and estimated values were presented in bar forms where blue bars are the actual values and red bars are the estimated one. The different validation criteria performance evaluations are shown in Table 2.
are the actual and estimated values based on the proposed model and N is the number of measurements used in the experiment, respectively. The neural network back propagation learning algorithm was able to perform the task properly by propagating the error each time reaching to the minimum error difference between the actual and the estimated values. In Figure 3, we show The ANN convergence curve. Figure 4 shows the actual and estimated values in both training and testing cases. The actual and estimated values were presented in bar forms where blue bars are the actual values and red bars are the estimated one. The different validation criteria performance evaluations are shown in Table 2.
5. Conclusion
In this study, we proposed an Artificial Neural Network

Figure 2. Developed neural network structure.

Figure 3. NNs convergence for 4 input and 1 output model.

Figure 4. Actual and estimated carbon emission in both training and testing cases.


Table 1. The data values of global oil, natural gas, coal, primary energy consumption and CO2 emission [22].

Table 2. MD, ED and MMER for ANN model training and testing data of the carbon estimation.
model to estimate the values of the carbon dioxide emitted. The ANN was trained by the backpropagation learning algorithm. The proposed ANN model results show that ANN was capable of producing high estimation capabilities. This is clearly seen from the obtained results and the shown relationship between the actual and estimated responses. Again the ANNs proved its ability in solving the carbon estimating problem from a given set of examples. We plan to explore the use of other soft computing techniques to solve this problem such as fuzzy logic and genetic programming.