Genetic Algorithm Works for Vectoring Image Outlines of Generic Shapes ()
1. Introduction
Fitting curves to the data extracted from generic planar shapes is the problem which is immensely worked on during last two decades. It still grabs the attention of researchers due to its applications in diverse fields and its demands in the industry. The process of vectorizing outlines of the images consists of several mathematical and computational phases and stages. This process aims to fit an optimal curve to the data extracted from the boundary of the image. Although many contributions in the literature [1-27] can be found in this area, there is still room for making more advancements and finding interactive approaches.
Least square fitting is common in optimization problems in which splines and higher order polynomials are used to approximate the data. One can see a cubic spline technique [1] with least square fitting. Squared distance minimization has been used on B-spline curves in [2]. It uses iterative process to achieve an optimal curve.
Instead of parametric form, implicit form of the polynomial is also used for this purpose. Implicit B-spline curves [3] are used to solve curve reconstruction problem by approximating the point clouds. It uses the heuristic of trust region algorithm. In [4,5], schemes were proposed for fitting implicitly defined algebraic spline curves and surfaces. This was achieved over the scattered data by simultaneously approximating points and associated normal vectors.
In this paper, a soft computing technique namely Genetic Algorithm (GA) [6] is proposed to find the optimal spline curves to the data extracted from the boundaries of the generic images. This evolutionary technique incorporates the corner points from the outline of the input image. The detection of corner points is quite significant as it helps minimizing the time to achieve desired curve to the outline of the image. Curve fitting in this scheme is done by using cubic spline which contains two shape parameters in its description. Basic target is to find those values of the parameters which assure minimum error between detected boundary of the image and the fitted spline curve.
The paper is organized in a way that the first and second steps (outline estimation and corner detection) of the proposed scheme are described in Section 2. A generalized cubic spline curve scheme is given in Section 3. Genetic Algorithm is explained in Section 4, Section 5 discusses the proposed scheme which is demonstrated with examples in Section 6. Finally, the paper is concluded in Section 7.
2. Countour Extraction and Segmentation
First step in proposed scheme of vectorization of planar objects is to extract data from the boundary of the bitmap image or a generic shape. In this procedure, a bitmap image of the generic shape is used as an input. In order to get the image, software like Paint and Adobe Photoshop can be used or some other appropriate way can be adopted. After saving the bitmap image to the system, the chain code method [7,8] is used to extract boundary of the image. Chain codes represent the direction of the image and help to attain the geometric data from outline of the image.
In the next step, the data extracted from the outline needs to be subdivided into smaller segments for curve fitting. For this purpose corner points or significant points are detected. Detection of these points is not an easy task as exactness of detected corners can only be judged by human eye and no other standard criterion exist. Then accuracy of any corner detection scheme can only be examined if the original corner positions are known. Generally corner detection can be defined as an approach which extracts the dominating features of an image and consequently helps deducing contents of the image. Plenty of corner detection schemes can be found in the literature [9-12]. In this paper, the scheme presented in [10] is used to divide the boundary into smaller segments. Each segment of the boundary consists of two consecutive corner points and the data points in between them. These corner points would be used for curve fitting.
3. Generalized Cubic Spline
Finding corner leads to subdivision of the data obtained by the boundary of the bitmap image into pieces. Each piece consists of two successive corner points and the data points in between them. Thus if there are m corner points F1, …, Fm then there will bem pieces P1, …, Pm. Each piece is treated separately and spline is fitted to it.
First piece consists of all the contour points in between F1 and F2 inclusive. Second piece contains all contour points in between F2 and F2 inclusive. Consequently, the mthpiece includes all contour points between Fm and F1 inclusive. In general, the ith piece contains all the data points between Fi and Fi+1 inclusive.
3.1. Cubic Spline Interpolant
As a curve fitting technique, the algorithm proposed in Section 5 makes use of a generalized cubic spline method. This spline embodies a number of desirable features needed for an optimum solution. The curve-fitting method employed here seeks the cubic spline for the determination of good shape parameters in its description.
Cubic spline function [13] is used for fitting curves at corner points. Let Fi, Fi+1,  be the two corner points of ith piece. Also let Di and Di+1 be the corresponding tangents at corner points. Then the cubic function, where
be the two corner points of ith piece. Also let Di and Di+1 be the corresponding tangents at corner points. Then the cubic function, where  and
and 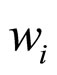 are shape parameters, is defined by:
are shape parameters, is defined by:
 (1)
(1)
where
 (2)
(2)
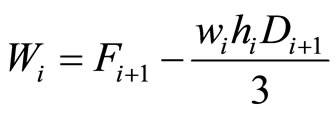 (3)
(3)

Equation (1) can be rewritten as:
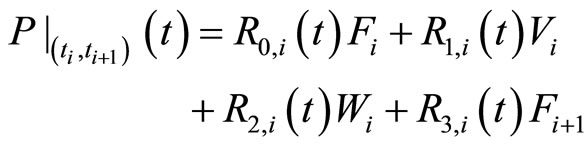 (4)
(4)
where
 (5)
(5)
The functions Rj,i, j = 0, 1, 2, 3 are Bernstein Bézier like basis functions, such that
 (6)
(6)
The cubic function (1) has the following properties:

 ,
,
 and
and ,
,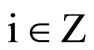 .
.
Figure 1 representscurve fitting to the given data by using cubic function (1) for assigning the different values to the parameters νi and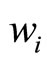 . The effect of different values of the shape parameters on the shape of the curve are also shown in Figure 1. In Figure 1(a) cubic curve (1) is fitted to the data with the values of parameters as: νi =
. The effect of different values of the shape parameters on the shape of the curve are also shown in Figure 1. In Figure 1(a) cubic curve (1) is fitted to the data with the values of parameters as: νi =  = 0, νi =
= 0, νi =  = 1, νi =
= 1, νi =  = 2 and νi =
= 2 and νi =  = 3. Figures 1(b) and 1(c) show cubic curves with parameters νi = 3,
= 3. Figures 1(b) and 1(c) show cubic curves with parameters νi = 3, 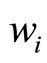 = 1 and νi = 1,
= 1 and νi = 1, 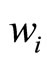 = 3 respectively.
= 3 respectively.
3.2. Parameterization
Number of parameterization techniques can be found in literature for instance uniform parameterization, linear or chord length parameterization, parabolic parameterization and cubic parameterization. In this paper, chord length parameterization is used to estimate the parametric value t associated with each point. It is as follows:
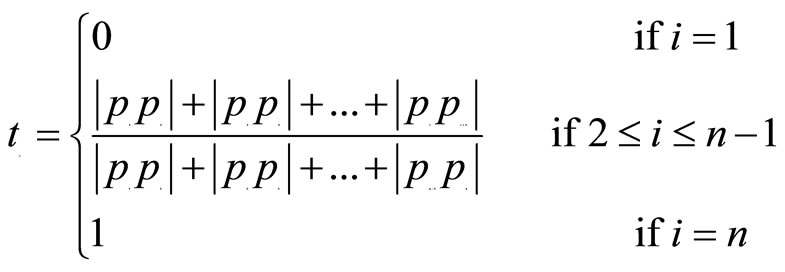
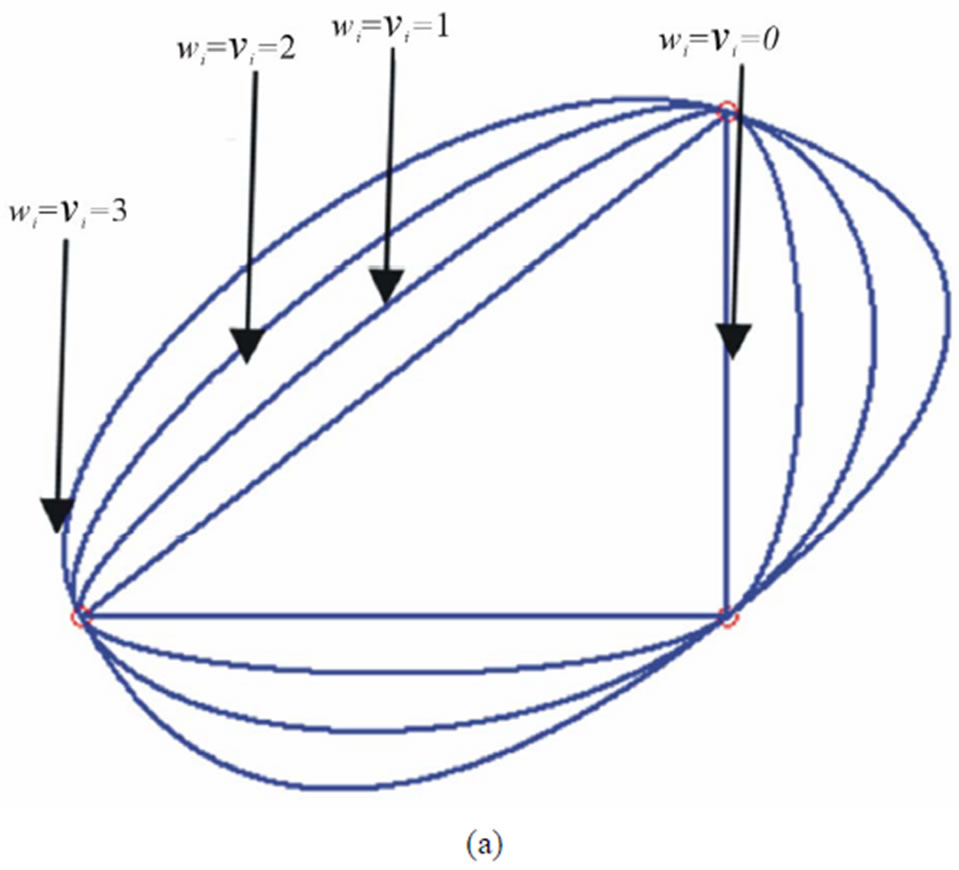


Figure 1. Demonstration of cubic function (1) for different values of parameters.
It can be observed that ti is in normalized form and varies from 0 to 1. Consequently, in our case, hi is always equal to 1.
3.3. Estimation of Tangent Vectors
A distance based choice of tangent vectors Di’s at Fi’s is defined as:
For open curves:
 (7)
(7)
For close curves:
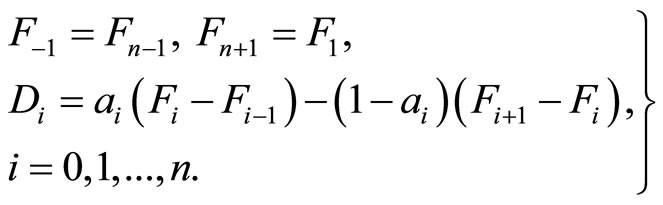 (8)
(8)
where
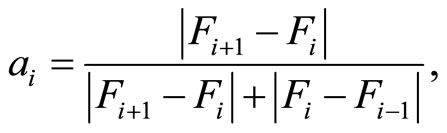 i = 0, 1, …, n. (9)
i = 0, 1, …, n. (9)
4. Genetic Algorithm
Genetic Algorithms (GAs) are the evolution based search techniques. In GAs, every solution, in a given well-defined search space, is represented by a bit string. This bit string is called a chromosome. Selection, crossover and mutation are the three operators used in agenetic algorithm. A GA creates a population of chromosomes iteratively and is attempted to improve on the quality of chromosomes.
A GA allows a populationcomposed of many individuals to evolve under specified selection rules toa state that maximizes the “fitness” (i.e., minimizes the cost function). A set of input variable, in the form of a chromosome solution, is represented in a well-defined search space. A cost function, which may be a game, or an experiment or a mathematical function, is used to generate an optimal output from the chromosome.
The GA begins by defining a chromosome or an array of variable values to be optimized. The variable values are represented in binary form, so the binary GA works with bits. However, the cost function normally needs continuous variable to use in its description. Therefore, the chromosome is decoded whenever the cost function is evaluated.
How, a chromosome is encoded in binary for, is shown in Figure 2.
The GA starts with a group of chromosomes known as the population. Next the variables are passed to the cost
function for evaluation. Natural Selection process leads to Survival of the fittest i.e. discarding the chromosomes with the highest cost. Natural selection occurs in each generation or iteration of the algorithm. It is somewhat arbitrary to discard the undesired chromosomes or to keep the desired ones. If only very few chromosomes are allowed to survive for the next generation, it limits the available genes in the offspring. Similarly, if too many chromosomes are allowed to stay for next generation, the bad performers get a chance to contribute to the next generation in a bad way. Therefore, to have a natural selection process, it is recommended to keep 50% of the chromosomes.
Thresholding is another approach to the process of natural selection. All the chromosomes having a cost value less than some threshold are assumed to be survived in this approach. In order that parents produce offspring, the threshold allows some of the chromosomes to continue. Otherwise, to find some chromosomes that pass the test, there would be the case that the whole new population would be generated. In the whole process, in the beginning, a small number of chromosomes may survive. However, in the generations afterwards, most of the chromosomes will survive provided the threshold is not changed.
In process of matchmaking, two chromosomes are selected from the mating pool of survived chromosomes to produce two new offspring. There are several schemes for parent selection like roulette wheel, tournament selection, random pairing etc. The next step after selecting parents is mating to create one or more offspring.
The crossover operator is a commonly used form of mating. It deals with two parents to produce two offspring. The first and the last bits of the parent’s chromosomes are used to randomly select a crossover point. The left of the crossover point to the first offspring is passed the binary code of the first parent. In the same way, the left of the crossover point to the second offspring is passed the binary code of the second parent. Moreover, the binary code to the right of the crossover point of first parent goes to second offspring and second parent passes its right side’s code to first offspring. As a result of crossover operator the offspring contain parts of both the parents. Crossover operator is demonstrated in Figure 3.
Another way of creating new chromosomes is mutation in which new traits can be introduced to chromosomes that are not present in the original population. A single point mutation changes a 1 to a 0, and vice versa is shown in Figure 4.
The process of GA described is iterated and would be repeated until the achievement of best solution for the problem. Flowchart of GA is shown in Figure 5.
5. Proposed Approach
In this Section the proposed scheme to the curve fitting problem is described. It includes the phases of problem matching with Genetic Algorithm using cubic spline function, description of parameters used for GA and curve fitting.
5.1. Problem Mapping
In this section Genetic Algorithm formulation of the pro-

Figure 3. Example of crossover operator.

Figure 5. Flow diagram of genetic algorithm.
blem discussed in this paper is described in detail.
Suppose, for i = 0, 1, …, n − 1, the data segments Pi,j = (Xi,j, Yi,j,), j = 1, 2, …, m are given as ordered sets of the universal set of data points. Then the squared sums Si’s of distance between Pi.j’s and their corresponding parametric points P(ti)’s on the curve are determined as
 i = 0, 1, …, n − 1where u’s are parameterized in reference to chord length parameterization. For the best fitting of the curve to given data, such values of parameter νi and
i = 0, 1, …, n − 1where u’s are parameterized in reference to chord length parameterization. For the best fitting of the curve to given data, such values of parameter νi and , are required so that the sums Si’s are minimal. Genetic Algorithm is used to optimize this value for the fitted curve. We start with initial population of values of νi and
, are required so that the sums Si’s are minimal. Genetic Algorithm is used to optimize this value for the fitted curve. We start with initial population of values of νi and  chosen randomly. Successive application of search operations to this population leads to optimal values of νi and
chosen randomly. Successive application of search operations to this population leads to optimal values of νi and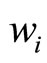 .
.
5.2. Initialization
Once we have the bitmap image shown in Figures 6(a), 7(a) and 8(a), the method of Section 2 is used to extract the boundary of the image. The boundary of the image is then used to detect the corner points in the next phase. It uses the corner detection method pointed out in Section 2. Figures 6(b) and 6(c), Figures 7(b) and 7(c) and Figures 8(b) and 8(c), show boundary of the bitmap images and detected corner points respectively. Table 1 gives number of contour points and initial corner points of the images.
5.3. Curve Fitting
Detection of the corner points leads towards the subdivision of the boundary of the image into segments. The interpolation spline of Section 3.1 is then used to approximate each segment of the boundary. This spline has the parameters v and w in its description. The initial solution of the parameters v and w is randomly selected. After an initial approximation for the segment is obtained, The GA is run to get the optimal solution of v and w. Genetic Algorithm helps to obtain better approximations to achieve optimal solution. The tangent vectors at knots are estimated by the method described in Section 3.3.
5.4. Breaking Segment
For some segments, the best fit obtained through iterative improvement may not be satisfactory. In that case, we subdivide the segment into smaller segments at points where the distance between the boundary and parametric curve exceeds some predefined threshold; such points are termed as intermediate points. A new parametric curve is fitted for each new segment as shown in Figures 6(e)

Table 1. Details of digital contours and corner points.
and 6(f), Figures 7(e) and 7(f) and Figures 8(e) and 7(f). In Table 2, number of intermediate points is presented which is obtained while fitting the optimized cubic spline for different iterations of GA.
6. Demonstration
Curve fitting scheme, proposed in Section 5 has been implemented on different images. In Figure 6, (a) represents original image, (b) shows outline of the image, (c)

Table 2. Number of corner points together with number of intermediate points for iterations 1, 2 and final iteration of GA along with total time elapse in running GA.
demonstrates corner points (d), (e) and (f) give fitted outline for 1st , 2nd and final iterations for threshold 3 respectively using Genetic Algorithms together with corner points and intermediate points). Figures 7 and 8 can also be described in similar fashion. Time elapsed for applying the proposed scheme for different images is given in Table 2.
Figures 9-13 show behaviors of fitness function for the image of fish on running GA again and again. It can be observed in Figure 9 that minimum value of cost function is achieved after iteration 20, whereas Figure 10 and Figure 11 indicate that minimum fitness function is obtained at iteration 10 and iteration 5 respectively. While Figures 12 and 13 depict a bit different behavior as in these cases initially fitness function increases and then it starts decreasing.
In Figure 14, stopping criteria followed to run GA is given and in Figure 15 best (^), worst (o) and mean (*) values of objective functions are shown in each iteration for the image of fish.Flowchart for proposed algorithm is given in Figure 16.
7. Conclusion
In this paper a scheme is presented which vectorizes the generic shapes. A cubic function is used for curve fitting and a soft computing technique genetic algorithm is used
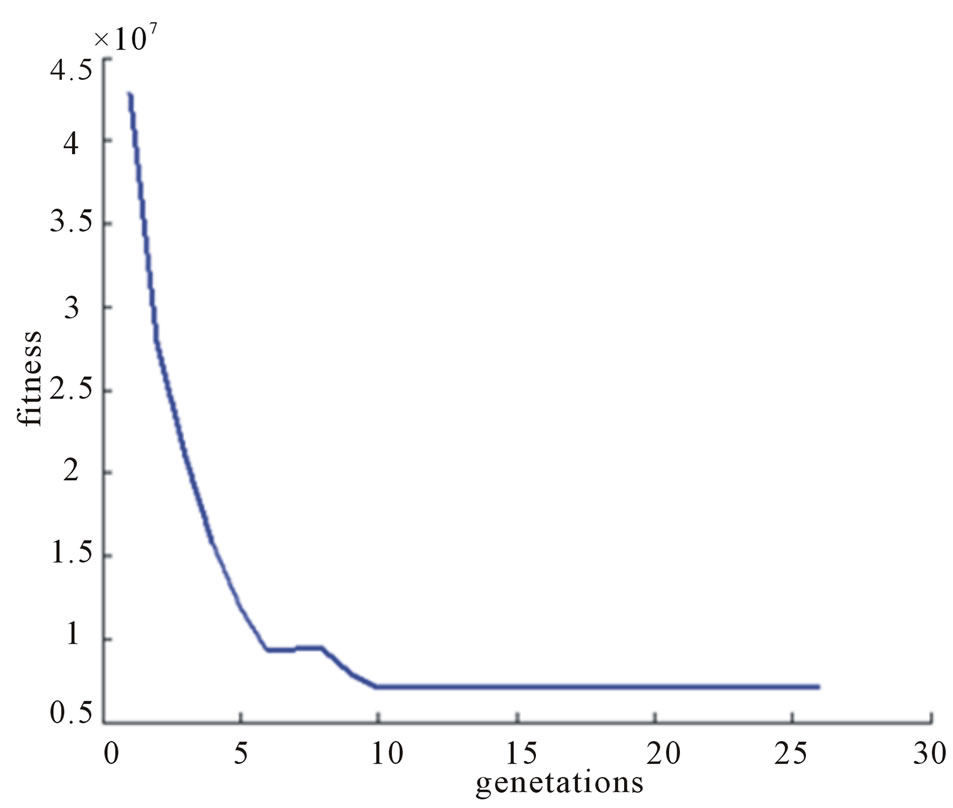
Figure 10. Behavior of fitness function.

Figure 11. Behavior of fitness function.

Figure 12. Mix behavior of fitness function.

Figure 13. Increasing and decreasing fitness function.

Figure 14. Stopping criteria met by GA in %.
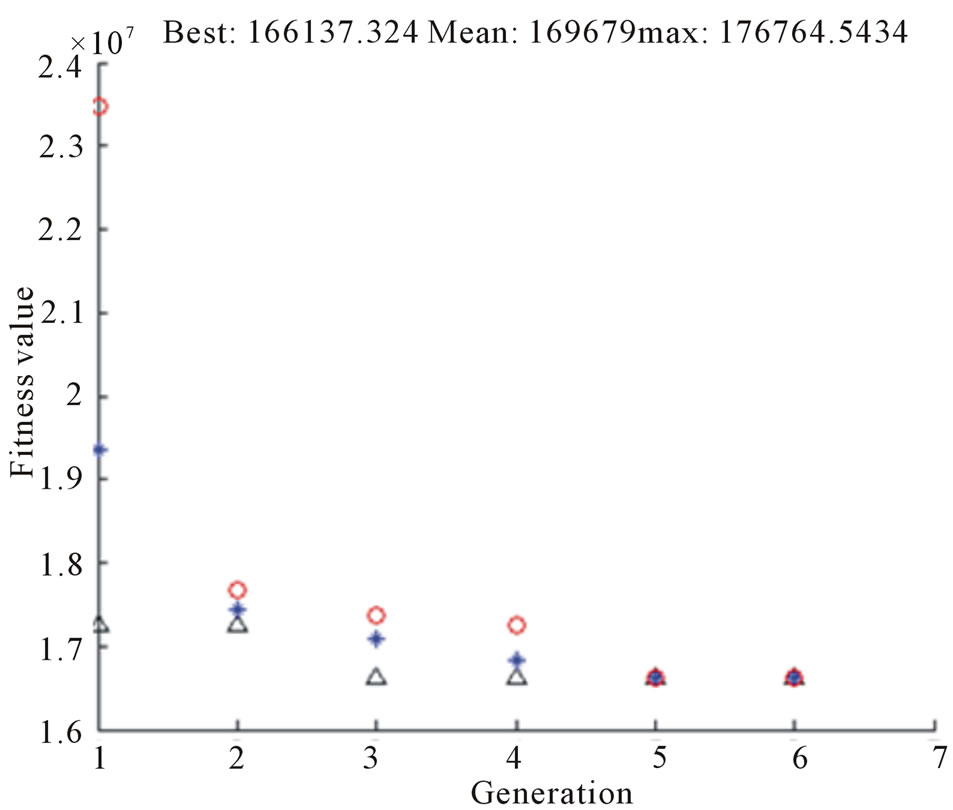
Figure 15. Best, worst and mean scores in different iteratons.
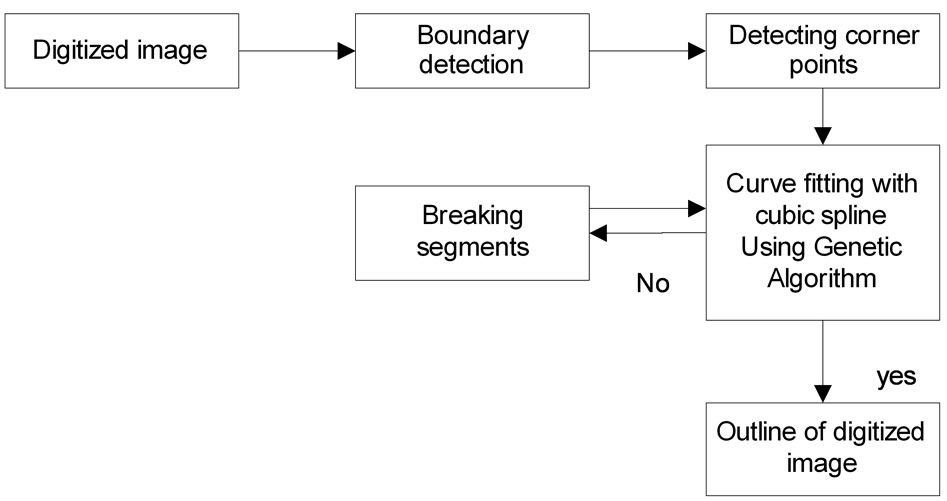
Figure 16. Outline of proposed algorithm.
to find optimal values of the parameters in the description of the cubic function. The method proposed starts with initial random population of parameters and finds those values of the parameters which can assure best optimal curve to the data extracted by bitmap images. The scheme presented is automatic and no human intercession is required. It also ensures computational efficiency as far as curve fitting is concerned.