Applying MILP for 27-Level CMLIs to Obtain Low THD Values over Wide Voltage Range ()
1. Introduction
Cascaded multilevel inverter (CMLI) is the most recent and popular type of multilevel inverters, that synthesizes a desired sinusoidal voltage from several separate dc voltage sources. The general construction of the CMLI is shown per phase in Figure 1. It consists of S number of H-bridges fed with dc voltages sources . The output voltage is usually constructed in a stair case shape with quarter wave symmetry, in Figure 2, to approach synthesizing a sinusoidal wave form, [1].
. The output voltage is usually constructed in a stair case shape with quarter wave symmetry, in Figure 2, to approach synthesizing a sinusoidal wave form, [1].
If all the dc sources are of equal value, say E, the CMLI is called symmetric. In this case the maximum number of the positive levels of the inverter is S and is obtained by switching on the dc sources sequentially, and these levels may take the values . While if the dc sources are of unequal values, the CMLI is referred to as an asymmetric CMLI. In this case the maximum number of the positive levels of the inverter can be increased greatly, since it could be possible to switch on some dc sources positively or negatively within the positive half cycle of the output voltage, thus adding additional positive levels. Generally, the possible positive levels of an asymmetric CMLI are all the positive values of
. While if the dc sources are of unequal values, the CMLI is referred to as an asymmetric CMLI. In this case the maximum number of the positive levels of the inverter can be increased greatly, since it could be possible to switch on some dc sources positively or negatively within the positive half cycle of the output voltage, thus adding additional positive levels. Generally, the possible positive levels of an asymmetric CMLI are all the positive values of , where each of
, where each of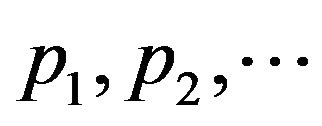 , and ps can take one of the values −1, 0 or +1. The number of all possible levels is (3)S, some of them may be redundant. Increasing the number of levels of the inverter means that its staircase output wave form can approach more closely a sinusoidal wave form, which in turn means that the output voltage lower order harmonic values and their total harmonic distortion could be reduced greatly, and this makes asymmetric CMLIs more popular for practical applications [2].
, and ps can take one of the values −1, 0 or +1. The number of all possible levels is (3)S, some of them may be redundant. Increasing the number of levels of the inverter means that its staircase output wave form can approach more closely a sinusoidal wave form, which in turn means that the output voltage lower order harmonic values and their total harmonic distortion could be reduced greatly, and this makes asymmetric CMLIs more popular for practical applications [2].
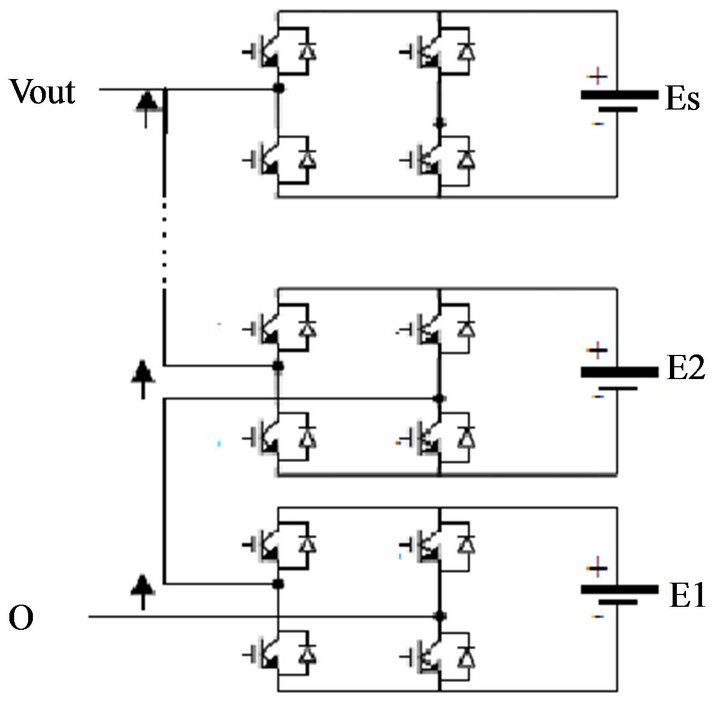
Figure 1. A cascaded multilevel with S dc sources.
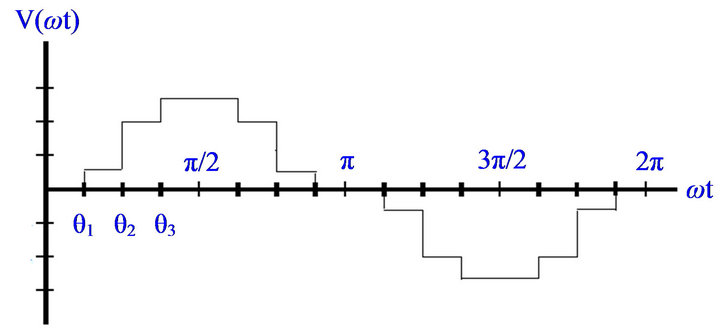
Figure 2. A staircase output voltage wave form with 3 positive levels.
To obtain a staircase output voltage wave form with equal step heights in an asymmetric CMLI, the following uniform step sufficient conditions may be satisfied by the dc sources . [3]:
. [3]:
1) ,
, 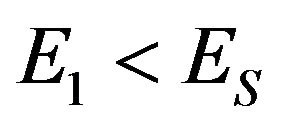 , and each of
, and each of 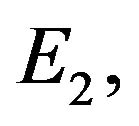
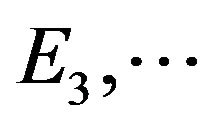 , and ES is an integer multiple of E1.
, and ES is an integer multiple of E1.
2)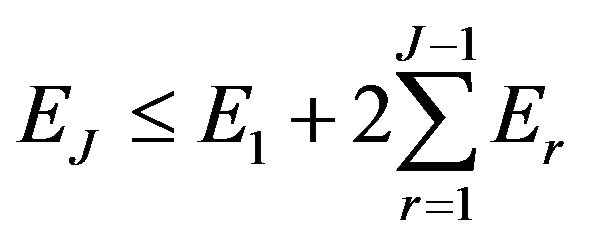 , and
, and 
It is possible to obtain the maximum number of levels in an CMLI, i.e. (3)S non-redundant or different levels, by replacing the inequality sign in the second condition with an equality sign. Thus considering three H-bridges with E1 = E we get E2 = 3E and E3 = 9E and the associated three H-bridges form the well known trinary asymmetric CMLI with the (3)3 = 27 levels: 
 and ±13E. Trinary asymmetric CMLIs can give better approximation of a sine wave than other asymmetric CMLIs, [4]. The 27-level asymmetric CMLI is thus recommended for many applications, such as for induction motors and traction drives, [5-7].
and ±13E. Trinary asymmetric CMLIs can give better approximation of a sine wave than other asymmetric CMLIs, [4]. The 27-level asymmetric CMLI is thus recommended for many applications, such as for induction motors and traction drives, [5-7].
In this paper the 27-level CMLI is considered, and a new approach depending on linear programming for determining the switching angles of this inverter that minimize the values of undesired harmonics is introduced and applied for single phase and three phase inverters.
2. A Proposed Approach for Determining the Switching Angles of the Inverter
A fundamental issue for a CMLI is to find the switching angles (times) of the inverter H-bridges semiconductor power switches that produce the required fundamental voltage and at the same time eliminate or reduce the values of undesired specific low order dominant harmonics .Many methods are given in the literature for obtaining the switching angles of symmetric as well as uniform step asymmetric CMLIs. These are mainly:
1) Using sinusoidal pulse width modulation, [8-12].
2) Using a selective harmonic elimination technique, where the zero equations of the undesired harmonics with the equation of the desired amplitude of the main harmonic as functions of the switching angles are solved directly or by applying genetic algorithms, [1,13-17].
3) Using the method of minimizing the total harmonic distortion, [18,19].
However, all these methods are suitable mainly for CMLIs with small number of positive levels, and thus are not adequate for the 27-level inverter with 13 positive levels.
In addition, the author has introduced a method based on a general linear programming model that could be applied to minimize the values of the undesired harmonics, [20,21]. This linear programming (LP) model has the following advantages over other methods discussed in the literature, [22]:
1) This model is flexible. It allows minimizing the values of harmonics of any order and any number, independent of the number of inverter levels, under any required reasonable value of the main harmonic.
2) LP constraints may be inequality constraints, so a feasible solution could be almost found, unlike harmonic elimination method which may give no feasible solution due to not satisfying the trigonometric equalities imposed.
3) LP constraints allow minimizing harmonics values with different weighting factors according to the harmonic order. Low order harmonics values could be minimized much more than higher order ones.
4) LP provides global optimal solution of the problem over the whole solution space, unlike some other optimization methods that give a local optimal solution near an initial solution, which may not be a global optimal solution.
5) Many software packages are available for solving LP models, even with huge number of variables and constraints, in a moderate time. They are suitable for large problems that could not be easily solved with other methods.
6) The model can be applied even for asymmetric CMLIs with non uniform steps by adding additional constraints, [23].
7) The model contains many parameters that could be selected arbitrarily. Many optimum solutions could be obtained for the same problem corresponding to different values of these parameters, and thus allowing for selecting the best one.
The mathematical model of this approach is first given, and then applied for the single phase and the three phase 27-level CMLI. The model is applied first to determine the number of harmonics to be minimized that lead to least %THD. By including this result in the model and solving it for different amplitudes of the output main harmonic, the switching patterns that give minimum values of undesired harmonics are obtained.
3. The Proposed Mathematical Model
The general uniform step asymmetric CMLI, or symmetric CMLI, is considered, where all the inverter levels are spaced equally with a step height E.. It is assumed, without loss of generality, that the inverter levels are equally spaced by 1 volt, i.e. normalized with respect to the dc voltage E. It is assumed also that the inverter output voltage wave form F(wt) has a quarter wave symmetry, as that shown in Figure 2. The pattern of this function is generated by on and off switching of the inverter H-bridges semiconductor power switches, and is completely determined by defining the switching pattern over the interval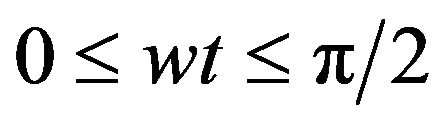 . The basic approach depends on dividing this interval into N equal small subintervals, starting at the angles
. The basic approach depends on dividing this interval into N equal small subintervals, starting at the angles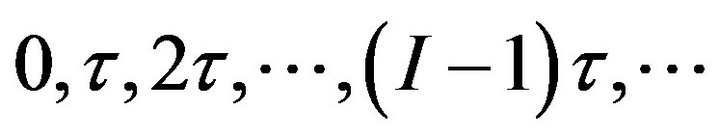 , till (N − 1)τ., where τ = π/2N, Figure 3.
, till (N − 1)τ., where τ = π/2N, Figure 3.
The positive integer values XI,  are defined over each subinterval, to represent the required instantaneous output voltage level value F(wt) of the inverter, so that F(wt) is defined over the interval
are defined over each subinterval, to represent the required instantaneous output voltage level value F(wt) of the inverter, so that F(wt) is defined over the interval 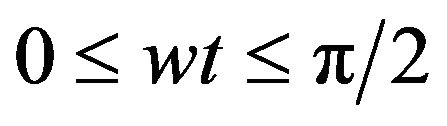 by:
by: 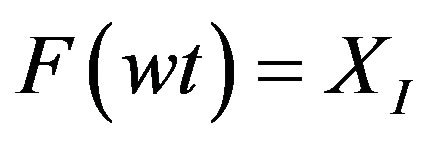 for
for  and
and 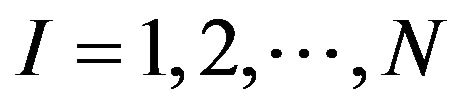
The Fourier series expansion of F(wt) is an odd-sines series given by:
 where
where
 (1)
(1)
where (2m + 1) is the order of the harmonic,  , τ = π/2N, and
, τ = π/2N, and .
.
The value of the amplitude of main harmonic corresponds to V1, and is obtained by substituting m = 0 in Equation (1).
Equation (1) shows that V2m + 1 for any value of m is a linear function of the integer values XI,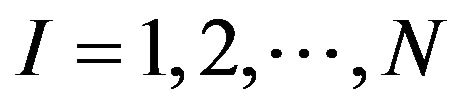 .
.
Variations of the values of XI from a subinterval to a next one determine the required switching angles of the inverter from one level to another.
It is required to find the values of XI that minimize the values of some undesired harmonics. A mixed integer linear programming (MILP) problem is formulated as
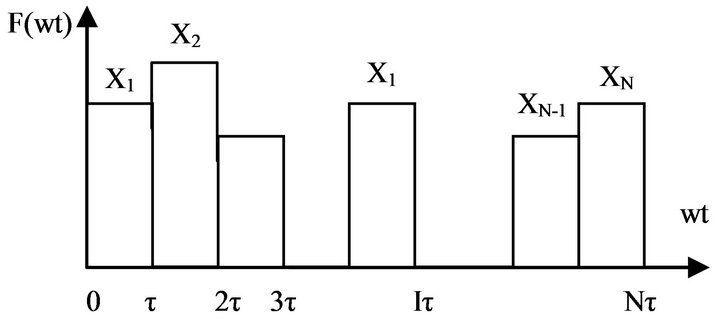
Figure 3. Representation of F(wt) by XI,  over the interval 0 ≤ wt ≤ π/2.
over the interval 0 ≤ wt ≤ π/2.
follows, [11]:
Minimize ε, subject to the constraints:
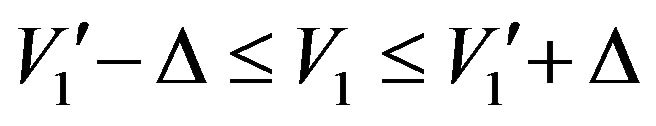 (2)
(2)
 (3)
(3)
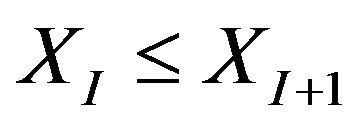 , for
, for , and
, and 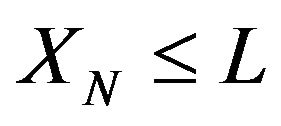 (4)
(4)
 and integer for
and integer for 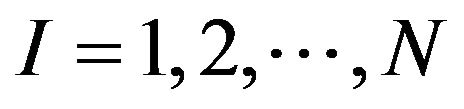 (5)
(5)
In the main harmonic constraint (2) 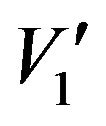 is the required amplitude of the main harmonic. Δ is a small incremental value,
is the required amplitude of the main harmonic. Δ is a small incremental value,  , arbitrary chosen and included in the main harmonic constrain to ensure obtaining an optimum solution, since an equality constraint may give a high value of ε or even an unfeasible solution., due to the trigonometric nature of the constraints. The value of Δ is taken of the order of 1% of
, arbitrary chosen and included in the main harmonic constrain to ensure obtaining an optimum solution, since an equality constraint may give a high value of ε or even an unfeasible solution., due to the trigonometric nature of the constraints. The value of Δ is taken of the order of 1% of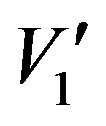 , so that the obtained value of V1 does not differ practically from the required value of
, so that the obtained value of V1 does not differ practically from the required value of .
.
In constraint (3) V2m + 1 is given by Equation (1), for V1 and the undesired harmonics, and α2m + 1 is a weighting factor for the undesired harmonics, to enable reduction of harmonics with different upper bounds according to their order.
By constraints (4) the positive staircase wave form shape is assured with maximum height L, where L is the number of positive voltage levels of the inverter.
Constraint (5) is the integer constraint on XI.
Once all the parameters of this MILP model are given, an optimum solution could be obtained that gives the values of XI and ε using any of the well known operations research software packages, e.g. “LINGO” software [24].
4. Selecting the Model Parameters
In the following sections this model is applied for the 27-level CMLIs, taking the number of subintervals N = 180, that corresponds to a subinterval angular width of 90˚/180 = 0.5˚, Figure 3.
The model is first solved with the constraint (2) replaced by:
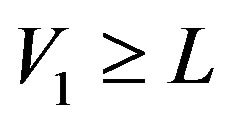 (2’)
(2’)
to minimize undesired harmonics for all amplitudes of the output voltage greater than L, normalized with respect to E, while utilizing all the levels of the inverter (L = 13).
The model is solved for the following two cases:
1) Minimizing all undesired harmonics equally, i.e. taking in constraint (3) the values of α2m+1 = 1 for all undesired harmonics.
2) Minimizing the harmonics with an increasing weighting proportional to the order of the harmonic, by taking α2m + 1= 2m + 1 for all undesired harmonics.
For each of the above two cases the model is solved for minimizing low order harmonics till a harmonic of order k, for different values of k, then selecting the value of k that leads to least %THD, where the %THD is defined by:
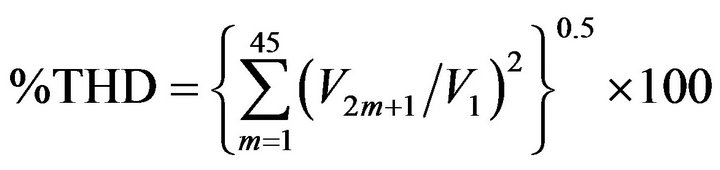 , (6)
, (6)
i.e. the %THD is calculated till the 91st harmonic.
Then the model is solved, using this value of k, to minimize low order undesired harmonics till the kth harmonic for different values of the required output voltage  between 7 and 15, using the constraint (2) and taking Δ = 0.1.
between 7 and 15, using the constraint (2) and taking Δ = 0.1.
By this way the switching patterns of the inverter at different values of the output voltage that minimize the values of low order harmonics with least %THD are obtained. This procedure is carried out next for the single phase and three phase CMLIs.
5. Solution of the Model for the 27-Level Single Phase CMLI
5.1. Solution for Different Values of the Undesired Harmonics
Figure 4 shows the %THD obtained by solving the model, with the voltage constraint (2’), to minimize the odd harmonics  till the kth harmonic for different values of k and for the two cases: equal weightings and increasing weightings of the undesired harmonics. The figure shows that the least %THD (= 2.67%) is obtained by minimizing the undesired harmonics equally till the 31st harmonic, and this is obtained at V1 = 13.21.
till the kth harmonic for different values of k and for the two cases: equal weightings and increasing weightings of the undesired harmonics. The figure shows that the least %THD (= 2.67%) is obtained by minimizing the undesired harmonics equally till the 31st harmonic, and this is obtained at V1 = 13.21.
5.2. Solution for Different Amplitudes of the Output Voltage
The model is solved using the voltage constraint (2) for some values of 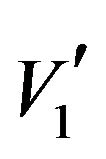 between 8 and 14 to obtain the switching angles of the inverter that minimize the odd harmonics equally from the 3rd till the 31st harmonic. Figure 5 shows for each value of V1, that corresponds to
between 8 and 14 to obtain the switching angles of the inverter that minimize the odd harmonics equally from the 3rd till the 31st harmonic. Figure 5 shows for each value of V1, that corresponds to
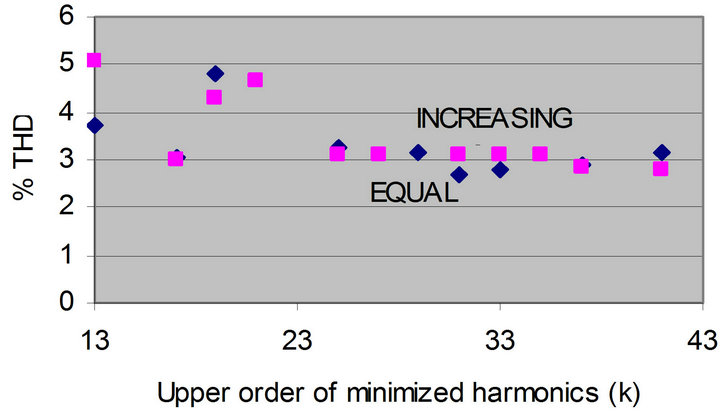
Figure 4. The %THD for different minimized harmonics.
 and 14, and for V1 = 13.21 the value of %THD and the value %Vhmax ,which represents the maximum percentage absolute amplitude of the undesired harmonics relative to the main harmonic among all harmonics from the 3rd till the 91st harmonic. It is shown that the % THD is less than 5% and that the %Vhmax is less than 3% over the wide voltage range.
and 14, and for V1 = 13.21 the value of %THD and the value %Vhmax ,which represents the maximum percentage absolute amplitude of the undesired harmonics relative to the main harmonic among all harmonics from the 3rd till the 91st harmonic. It is shown that the % THD is less than 5% and that the %Vhmax is less than 3% over the wide voltage range.
Some results obtained from the detailed solution of the model at V1 = 13.21 are given next. The value of %THD = 2.67% and of %Vhmax = 0.9%. For this value of V1 Figure 6 shows the obtained values of XI. The 13 switching angles of the inverter are: 1.5˚, 4.5˚, 10.5˚, 15.5˚, 19˚, 25˚, 29˚, 35˚, 39.5˚, 46.5˚, 52.5˚, 60.5˚ and 71˚. Figure 7 shows the switching patterns of the three H-bridges of the inverter during the positive quarter cycle of the main harmonic, assuming a uniform step asymmetric CMLI. The 1E H-bridge is switched 9 times on and 8 times off. The 3E H-bridge is switched 3 times on and 2 times off and the 9E H-bridge is switched one time on. If the 27
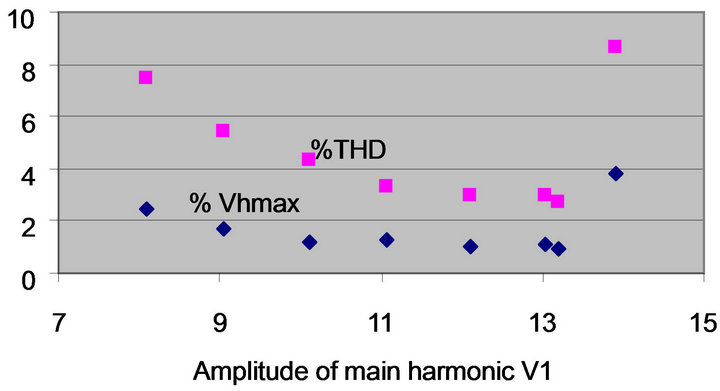
Figure 5. The values of %THD and %Vhmax against V.

Figure 6. Values of XI that gives V1 = 13.21.

Figure 7. Switching patterns of the H-bridges for V1 = 13.21.
level inverter is constructed as a symmetric CMLI it will need 13 H-bridges, that would be switched on consequently 13 times only during the positive quarter cycle of the main harmonic. This shows that asymmetric CMLIs suffer from more switching losses than symmetric CMLIs, but this does not represent a serious problem with recent developments of semiconductor power switches with low switching losses, [25].
Figure 8 shows the obtained percentage values of the harmonics relative to the main harmonic from the 3rd till the 91st harmonic, and a 5% of the main harmonic at V1 = 13.21.
Similar results could be obtained when solving the model at any value of the output voltage V1 between 8 and 14.
Noting that the values of V1 are normalized with respect to the dc voltage E.
6. Solution of the Model for the 27-Level Three Phase CMLI
In a balanced three phase operation the triplen odd harmonics, i.e. the 3rd, 9th, 15th··· and so on, are self cancelled in the output line voltage assuming a star connected three phase inverter. The procedure carried out in Section 5 with the single phase asymmetric CMLI is repeated while excluding the triplen odd harmonics, as follows:
6.1. Solution for Different Values of Undesired Harmonics
Figure 9 shows the %THD obtained by solving the model, with the voltage constraint (2’), to minimize the nontriplen odd harmonics till the kth harmonic for different values of k and for the two cases: equal weightings and increasing weightings of the undesired harmonics.
The figure shows that the least %THD (=1.67%) is obtained by minimizing the undesired harmonics equally till the 31st harmonic, and this is obtained at V1 = 13.87.
6.2. Solution for Different Amplitudes of the Output Voltage
The model is solved using the voltage constraint (2) for

Figure 8. % Values of harmonics for V1 = 13.21.
some values of 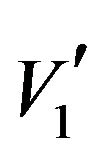 between 6 and 15.5 to obtain the switching angles of the inverter that minimize the non-triplen odd harmonics equally from the 5rd till the 31st harmonic. Figure 10 shows for each value of V1, that correspond to
between 6 and 15.5 to obtain the switching angles of the inverter that minimize the non-triplen odd harmonics equally from the 5rd till the 31st harmonic. Figure 10 shows for each value of V1, that correspond to 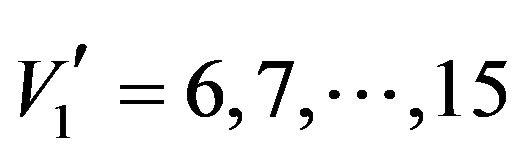 and 15.5, and for V1 = 13.87 the values of % THD and %Vhmax, as defined in Sections 4 and 5, for the non-triplen harmonics from the 5th till the 91st harmonic. It is shown that the % THD is less than 2.5% and that the %Vhmax is less than 1.5% over the voltage range 13 ≤ V1 ≤ 15, noting that the values of V1 are normalized w. r. t. E.
and 15.5, and for V1 = 13.87 the values of % THD and %Vhmax, as defined in Sections 4 and 5, for the non-triplen harmonics from the 5th till the 91st harmonic. It is shown that the % THD is less than 2.5% and that the %Vhmax is less than 1.5% over the voltage range 13 ≤ V1 ≤ 15, noting that the values of V1 are normalized w. r. t. E.
As a detailed solution example, the least values of % THD and % Vhmax are obtained at V1 = 13.87: % THD = 1.67% and % Vhmax = 0.69%. For this value of V1, Figure 11 shows the obtained values of XI.. The 13 switching angles of the inverter are: 2˚, 3˚, 8.5˚, 13.5˚, 17˚, 20˚, 24.5˚, 28.5˚, 33.5˚, 39.5˚, 49.5˚, 52.5˚ and 69˚.
Figure 12 shows the corresponding switching patterns of the three H-bridges of the inverter during the positive quarter cycle of the main harmonic, assuming a uniform